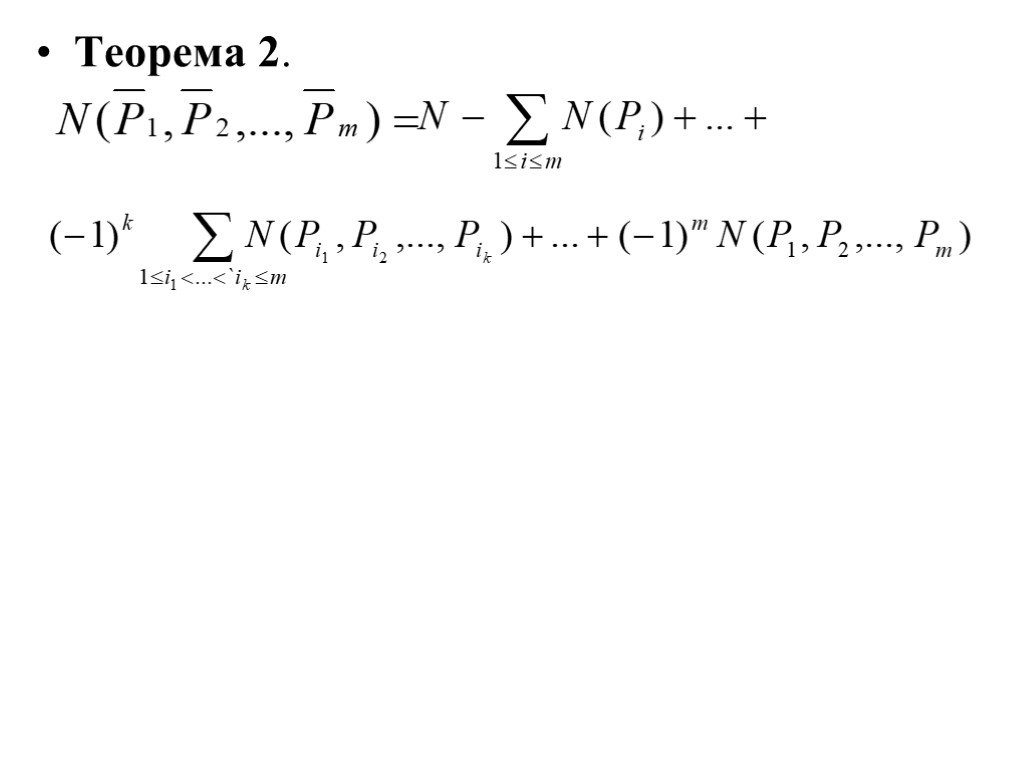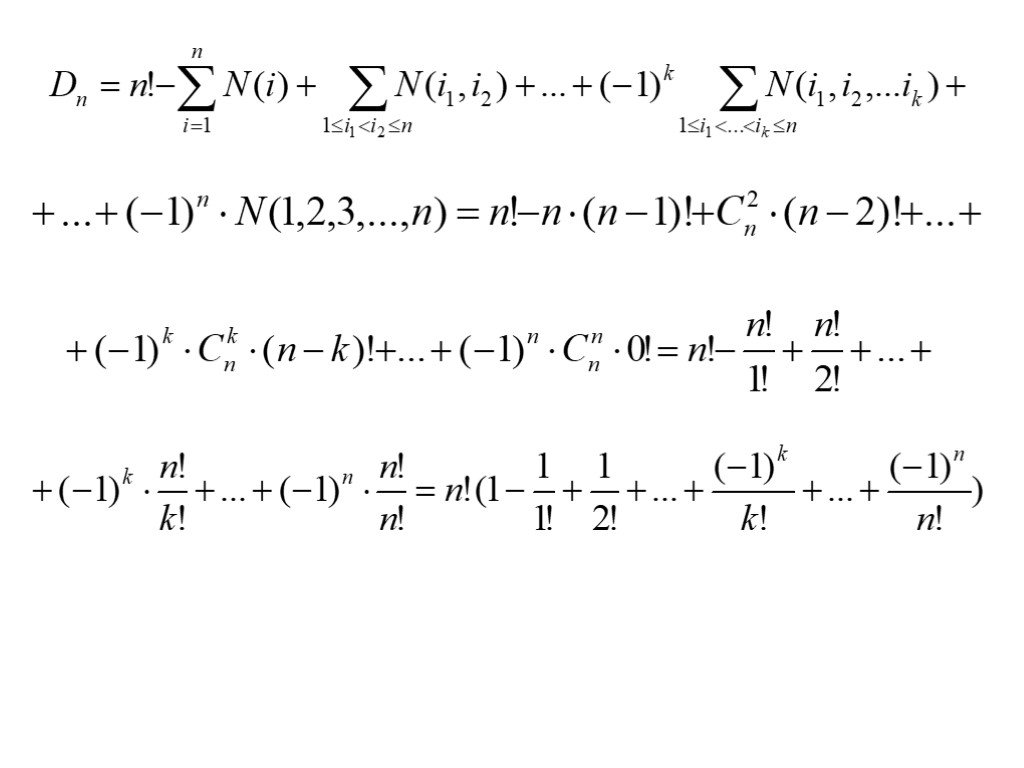Презентация "Формула включений-исключений. Беспорядки" по математике – проект, доклад
Презентацию на тему "Формула включений-исключений. Беспорядки" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 13 слайд(ов).
Слайды презентации
Список похожих презентаций
Арифметическая прогрессия. Формула n-го члена арифметической прогрессии
Историческая справка. Задачи на обе прогрессии встречаются у вавилонян, в египетских папирусах, в древнекитайском трактате «Математика в 9 книгах». ...Формула решения квадратных уравнений
Вступление. Данная работа может быть использована на обобщающем уроке по теме «Решение квадратных уравнений»с целью повторения и обобщения изученного ...Формула спелого арбуза
Цели, задачи, актуальность. Цель Выявление наиболее приемлемой математической формулы для определения спелости арбуза. Задачи Сбор информации об истории ...Формула полной вероятности. Формула Бейеса
Терминология. Допустим, что об условиях опыта можно сделать n исключающих друг друга предположений (гипотез): H1,H2,…,Hn, где Hi Hj = Ø, i ≠ j Hi ...Формула разности квадратов
a – b a+b (a + b)(a – b) a2 – b2 (a – b)2. Прочитайте выражения. разность чисел а и b сумма чисел а и b произведение суммы и разности чисел а и b ...Формула Пика
Получаем, S = 28 + 20/2 - 1 = 37 кв.ед. S= 5+4/2 -1=6 S=7+8/2-1=10. ...Формула площади прямоугольника
Цели урока. актуализировать знания учащихся о площади, полученные в начальной школе; дать понятие равных фигур; продолжить работу над текстовыми задачами; ...Формула Бернулли
Pn(k)=Ckn pk(1-p)n-k. Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность Pn(k) того, что событие A наступит k раз ...Формула Герона
. Герон Александрийский ( вероятно I век). Древнегреческий ученый. Работал в Александрии. Математические работы Герона являются энциклопедией античной ...Повторение опытов. Формула Бернулли
Опыты называются независимыми, если вероятность того или иного исхода каждого опыта не зависит от того, какие исходы имели другие опыты Независимые ...Формула арифметической прогрессии
Проверим глубину знаний. а1, а2, …, аn, … Как найти d? Записать формулу для n-го члена арифметической прогрессии. Записать формулы для нахождения ...Площадь. Формула площади прямоугольника
Площадь. Формула площади прямоугольника. S – площадь прямоугольника. S = a · b а b. 1. Найдите площадь закрашенных фигур. 2. Нарисуйте три разные ...Площади. Формула площади прямоугольника
3 м 9 м 4 м 7 м. Найдите площадь пола детской комнаты. S = 45 м2 1 2 4 5. . Площадь. Формула площади прямоугольника. 1. Площади равных фигур равны. ...Интеграл. Формула Ньютона-Лейбница с элентами поготовки к ЕГЭ
Тема: Интеграл. Формула Ньютона-Лейбница. Цели урока: Отработка навыков вычисления интеграла; Нахождение площади фигур с помощью формулы Ньютона-Лейбница; ...Формула одновременного движения
Проверка(№2). U(сбл.) = U + U d (расстояние за некоторую единицу t) = S – (U + U)x t t (встр.) = S : (U + U). Проверка №3. Формула одновременного ...Формула корней квадратного уравнения
Вы хотите научиться решать квадратные уравнения? ДА НЕТ. . . Содержание. Определение квадратного уравнения Дискриминант квадратного уравнения Формула ...Формула отрезков
. Теория. Общее определение. Особую часть задач на построение представляют собой задачи на построение по формуле, обычно они имеют следующий вид: ...Формула корней квадратного уравнения
Устный опрос. 1.Дайте определение квадратного уравнения,приведите примеры. 2.Назовите коэффициенты а,в,с в уравнениях: 3x2-5x+2=0; -5x2+3x-7=0, x2+2x=0; ...Формула Пика
. Вычислите площадь многоугольника. Задача: найти площадь многоугольника. Формула Пика. Площадь многоугольника с целочисленными вершинами равна В ...Формула корней квадратного уравнения
Сегодня на уроке мы будем:. записывать квадратные уравнения; вспоминать формулы нахождения корней квадратного уравнения; решать квадратные уравнения ...Конспекты
Формула пути. Решение задач на движение
Муниципальное бюджетное образовательное учреждение. « Лицей №28 г. Йошкар – Олы». Урок математики, проведенный в 3 Б классе. ...Формула работы
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 1909. г. Москва, 109153, улица Маршала Полубоярова, дом 12. телефон 705-5011, факс 704-40-51. ...Формула объема прямоугольного параллелепипеда
ОТКРЫТЫЕ УРОКИ. Учитель: Забродина Н.Д. 3 класс. Урок математики. Тема:. Формула объема прямоугольного параллелепипеда. Цели:. Углубить ...Формула произведения
Кубасова Людмила Евгеньевна. Учитель начальных классов. МБОУ СОШ № 5 г.Королёва Московской области. Открытый урок по ...Формула корней квадратного уравнения
Тема урока: «Формула корней квадратного уравнения». «Дорогу осилит идущий,. . а математику мыслящий». Цели урока:. выявить уровень усвоения ...Формула корней квадратного уравнения
Урок по теме «Решение квадратных уравнений по формуле»(слайд 1). Цели урока:. познакомить с формулой корней квадратного уравнения и учить применять ...Определение арифметической прогрессии. Формула n-го члена
« Определение арифметической прогрессии. Формула n. -го члена». 9 класс. Титова Таисия Алексеевна. МОУ СОШ №2. с.Чернолесского. ...Формула суммы членов конечной геометрической прогрессии
Схема конспекта урока. Тема. : «Формула суммы членов конечной геометрической прогрессии». Класс: 9. Тип урока. : урок изучения и первичного ...Геометрическая прогрессия. Формула n-го члена геометрической прогрессии
Конспект урока. Учитель: Кононенко Дмитрий Юрьевич. Предмет:. математика. . . Класс 9. Тип урока:. урок изучения нового материала по теме ...Интеграл. Формула Ньютона-Лейбница
Урок по теме «Интеграл. Формула Ньютона-Лейбница». . Учитель математики МКОУ «Волчихинская СШ» Бакута Елена Петровна. Тема. : Интеграл. Формула ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:23 января 2019
Категория:Математика
Содержит:13 слайд(ов)
Поделись с друзьями:
Скачать презентацию