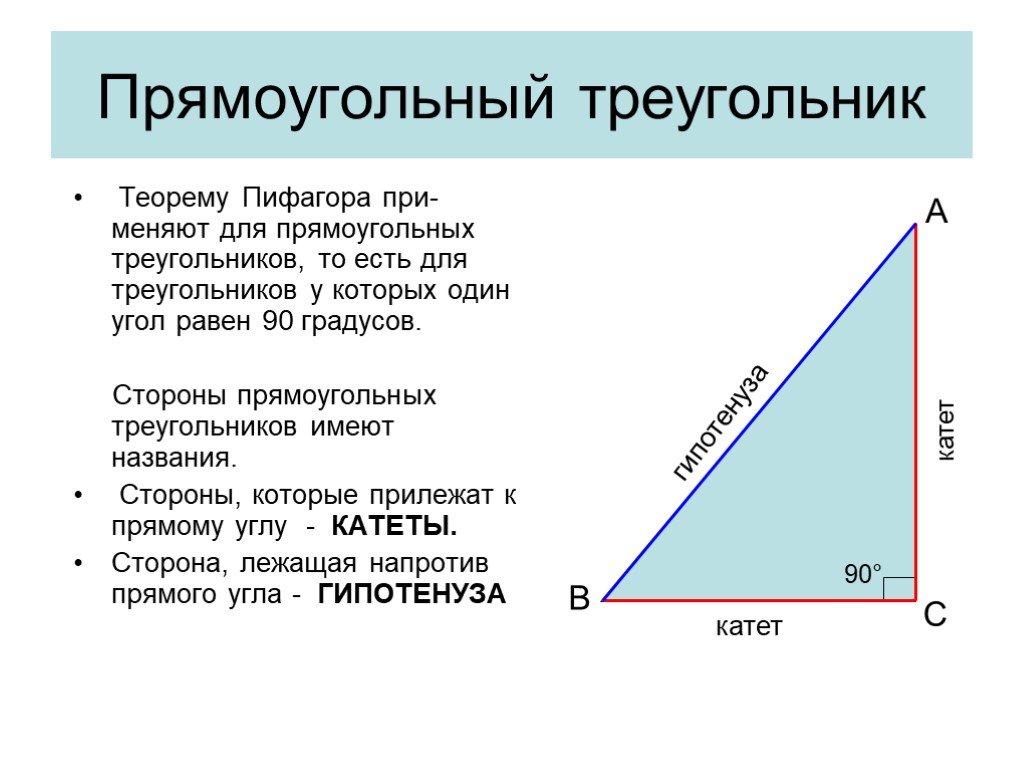
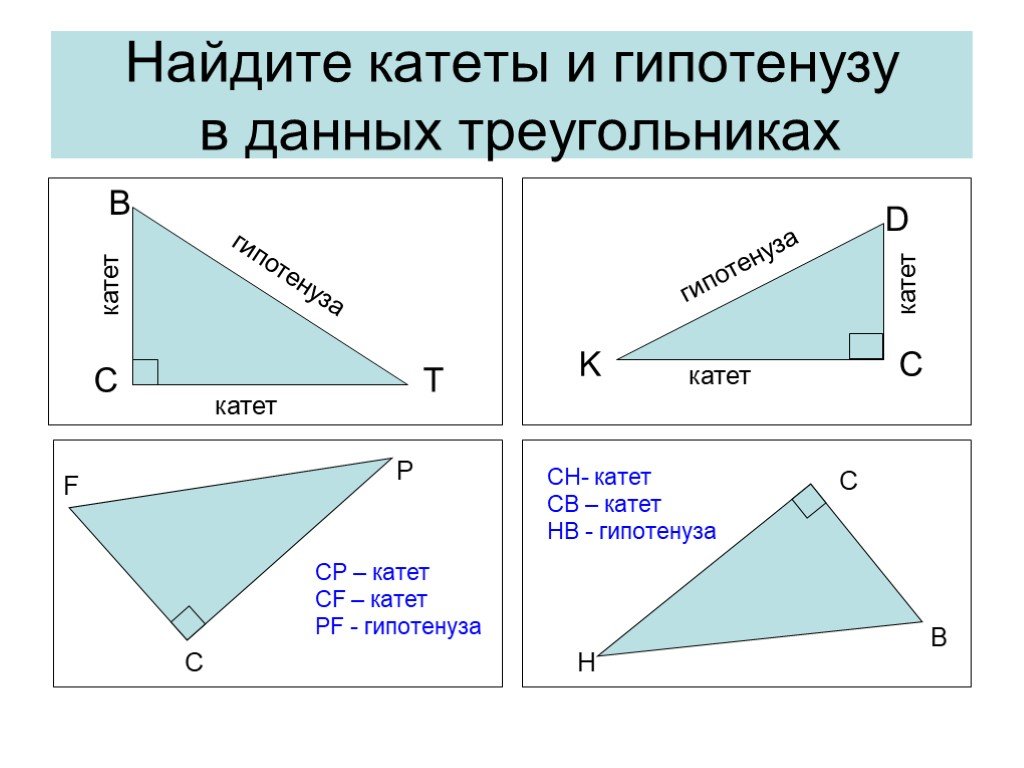
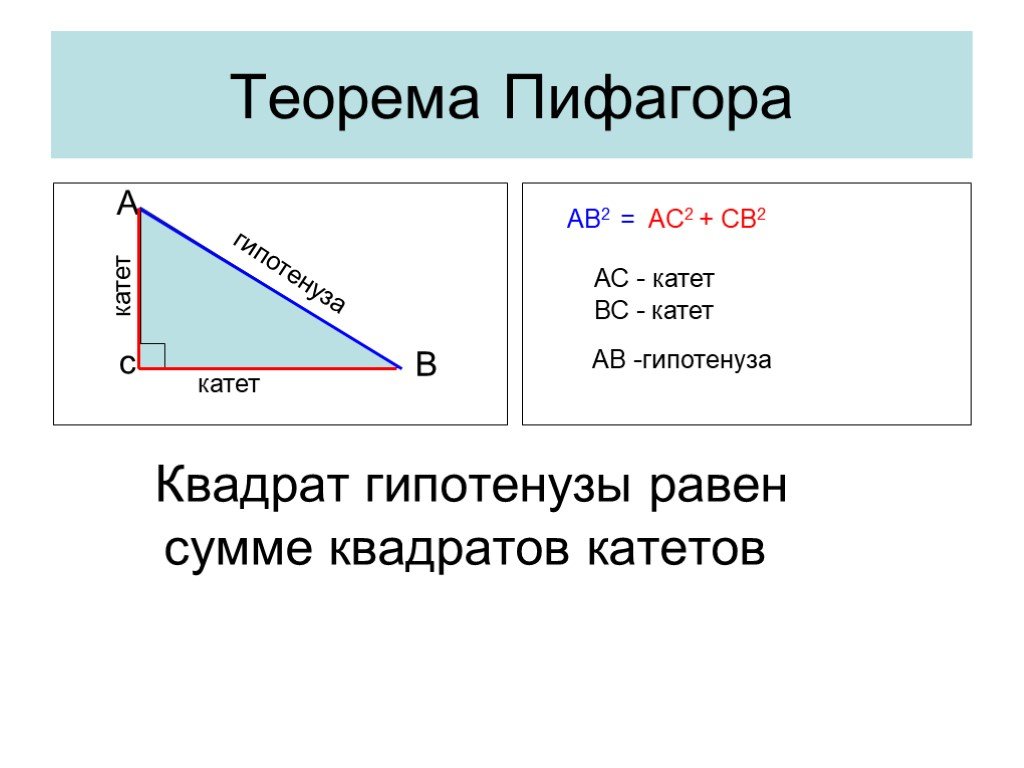
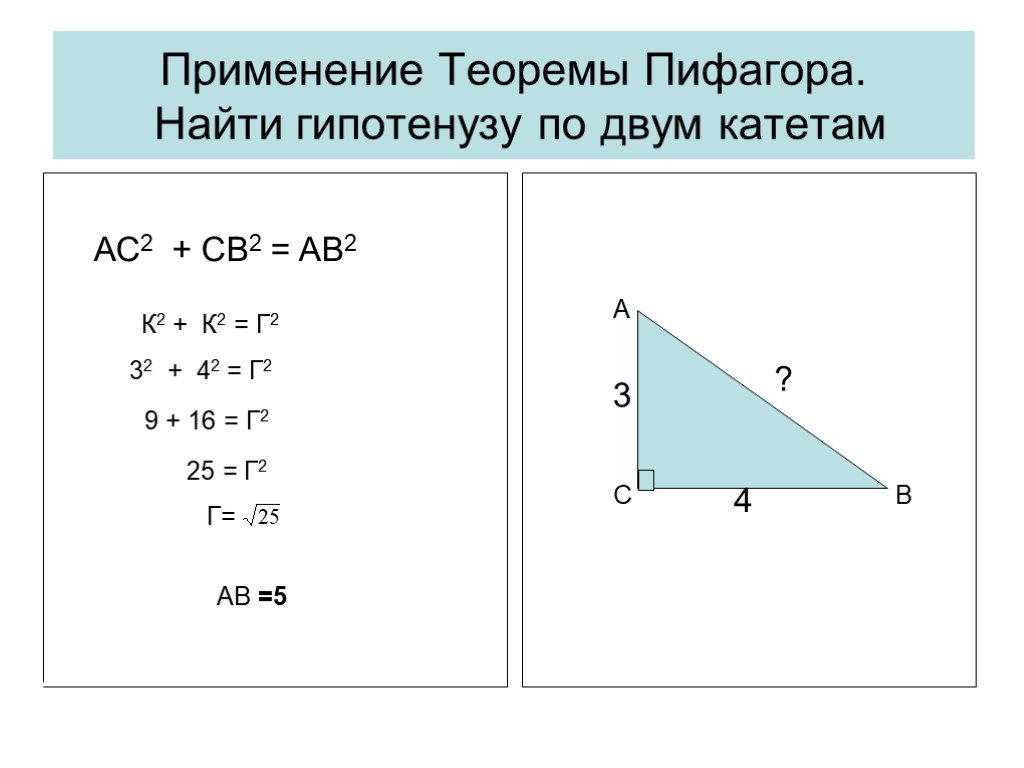
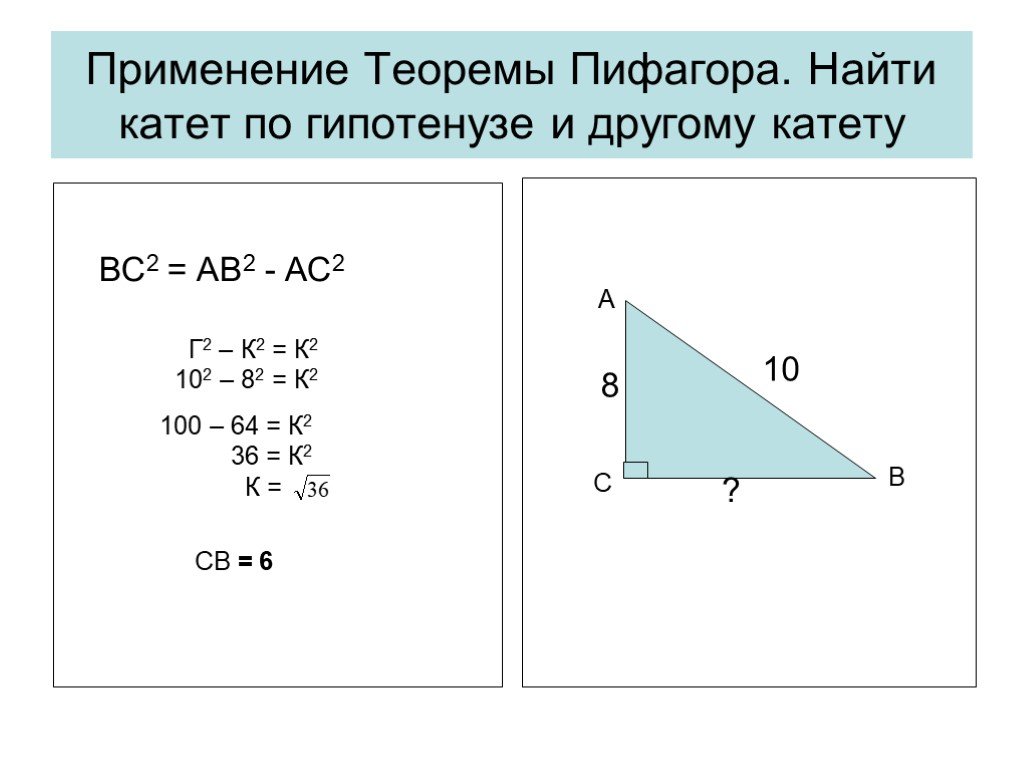
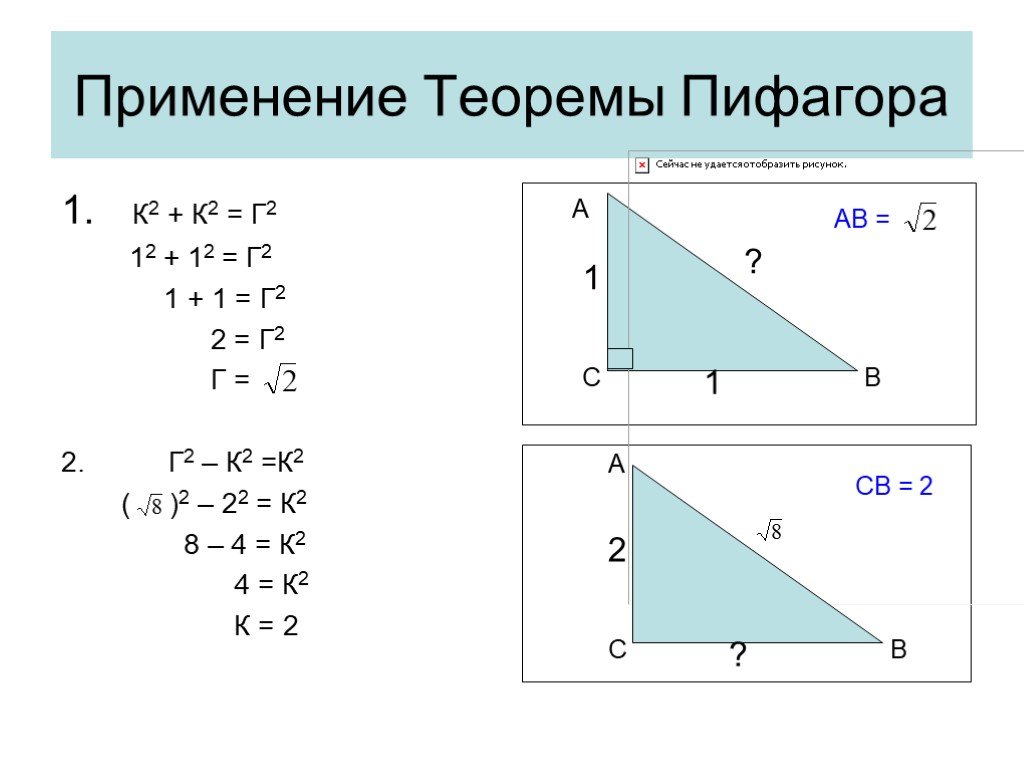
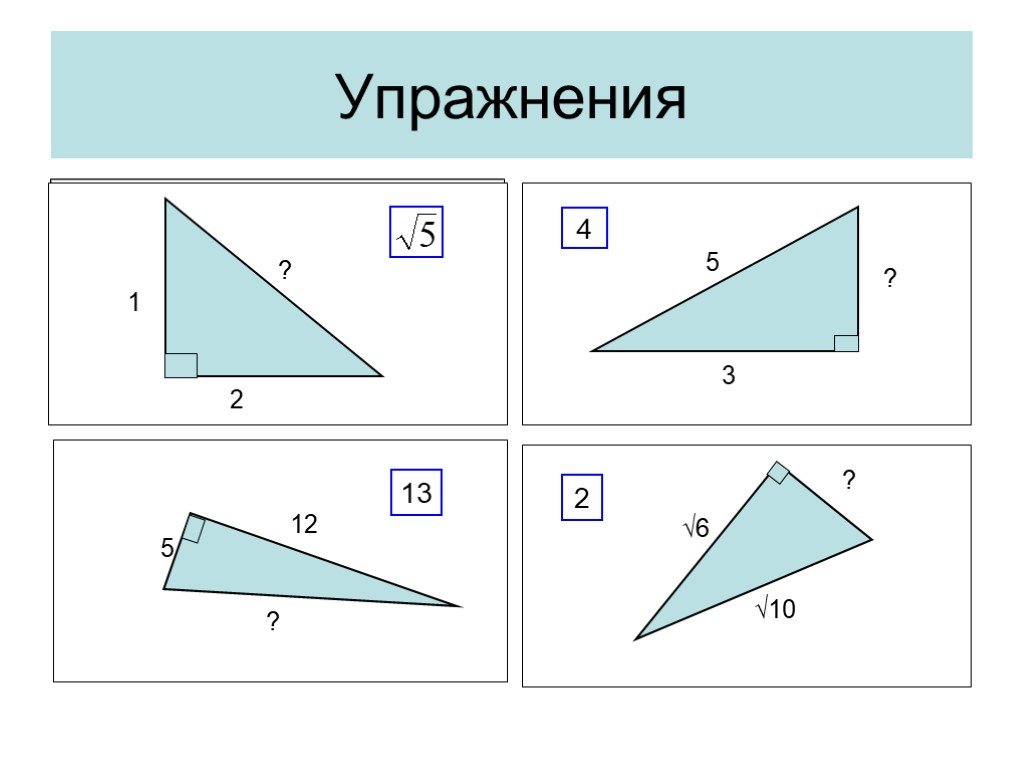
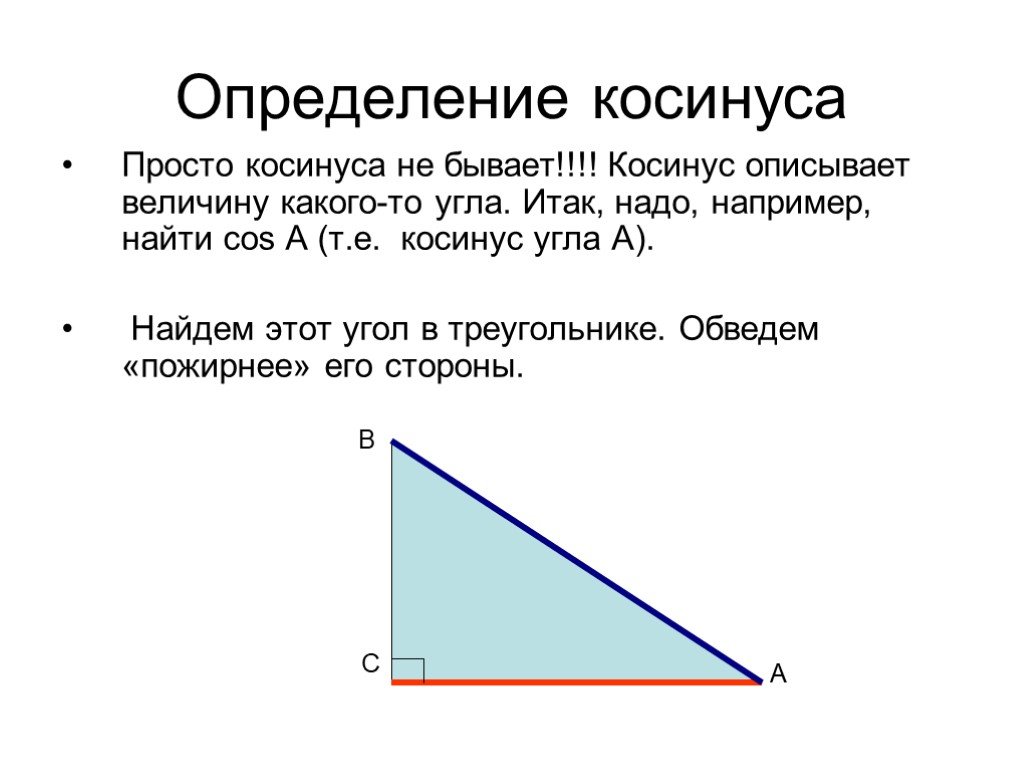
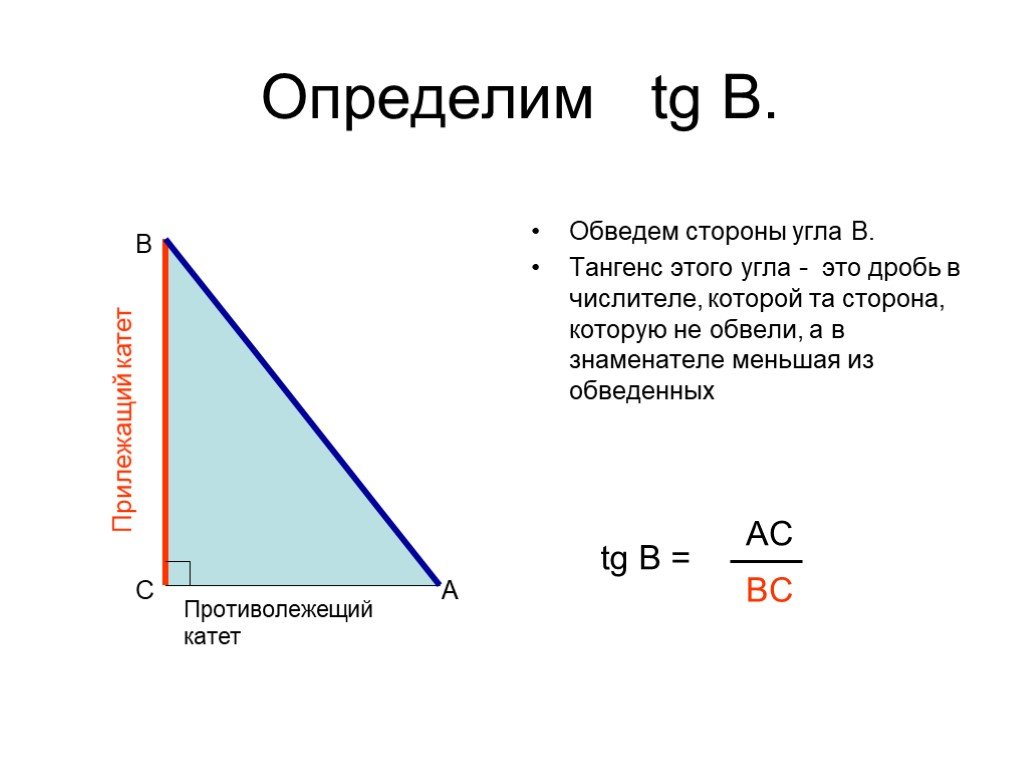
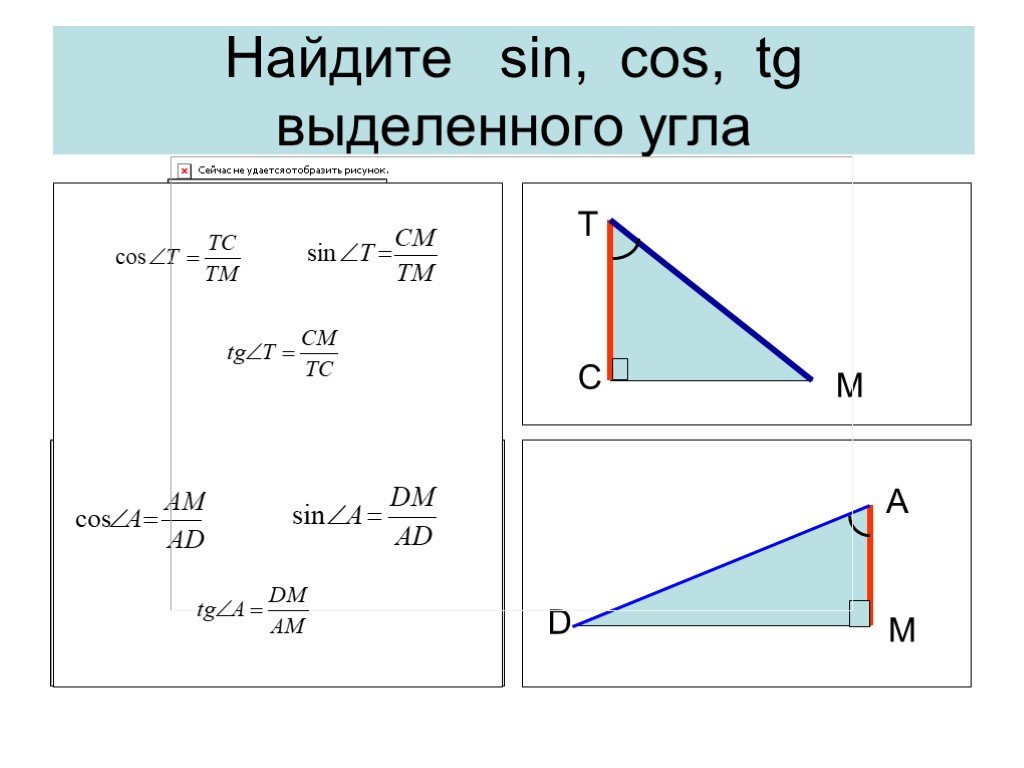
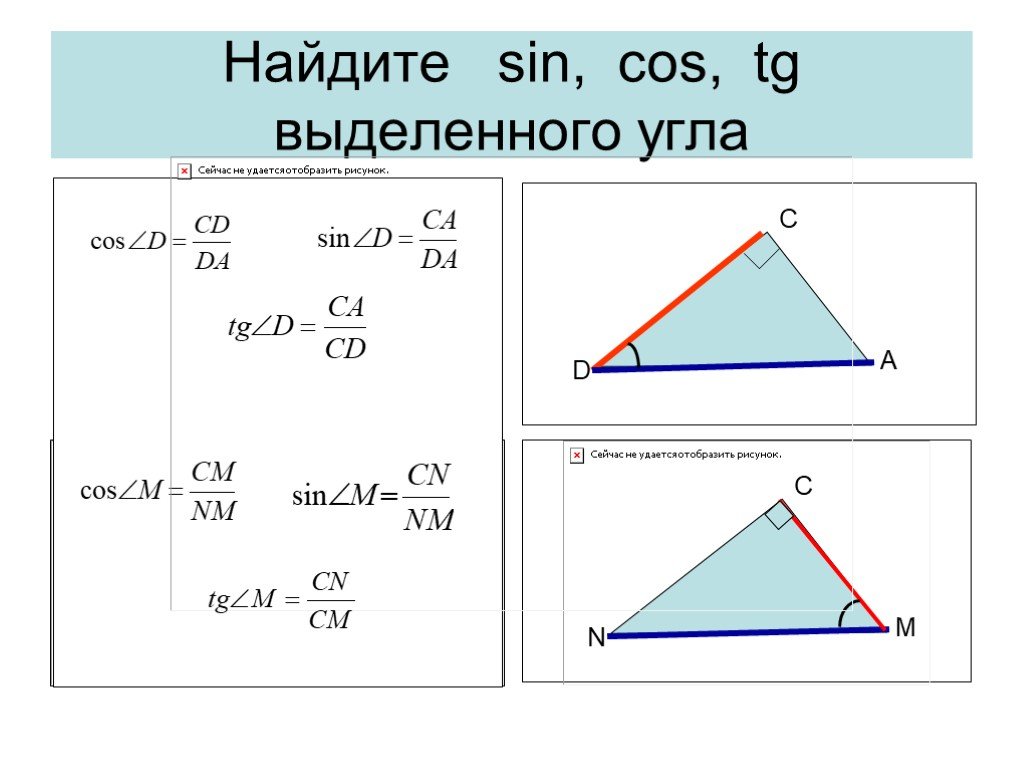
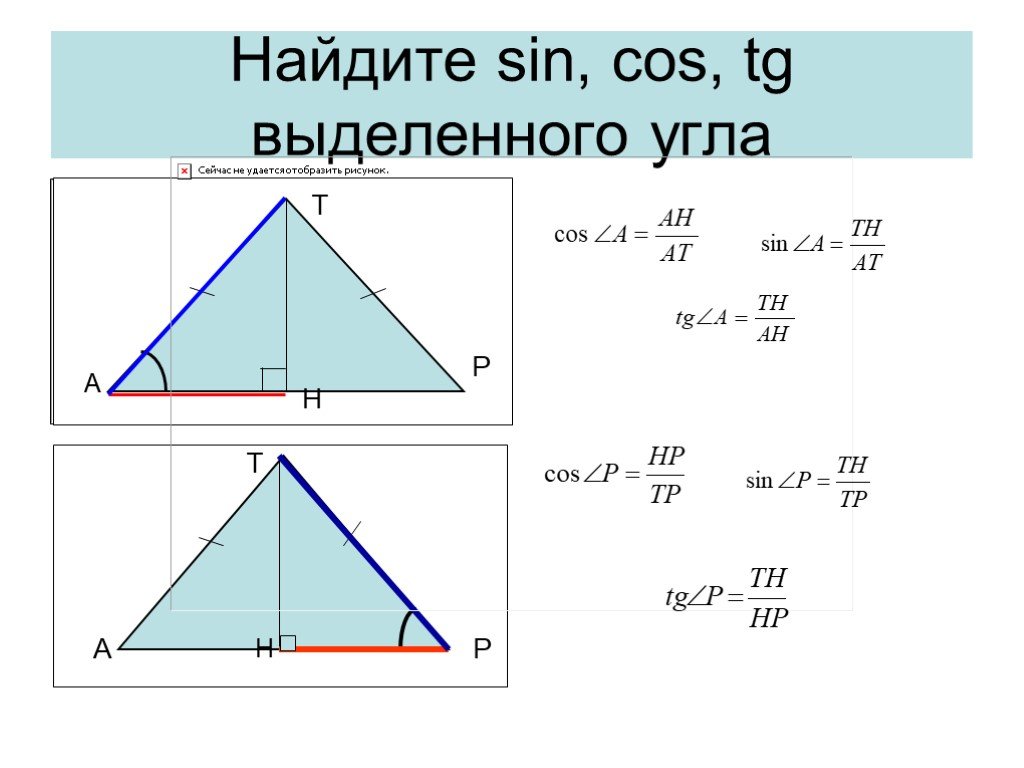
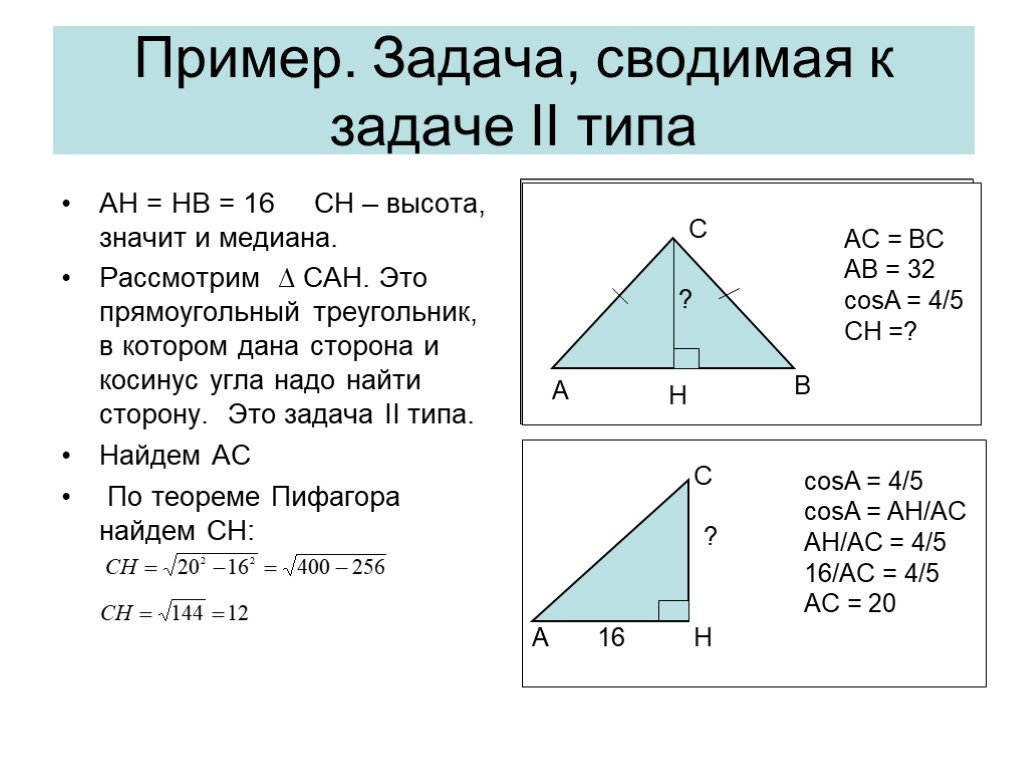
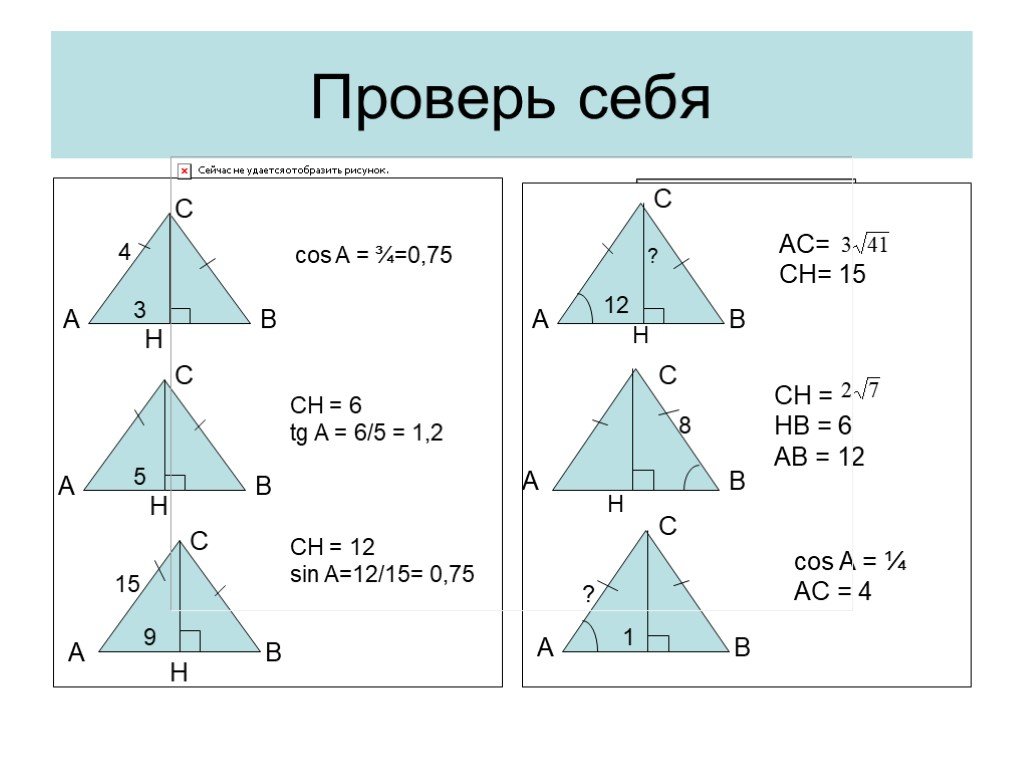
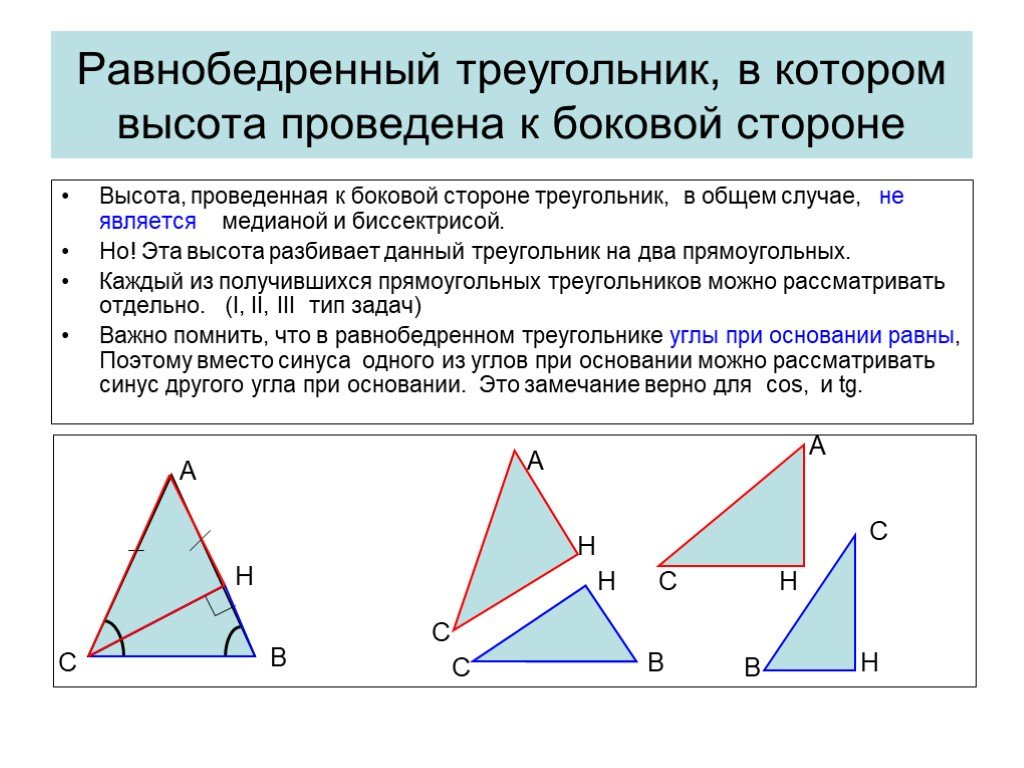
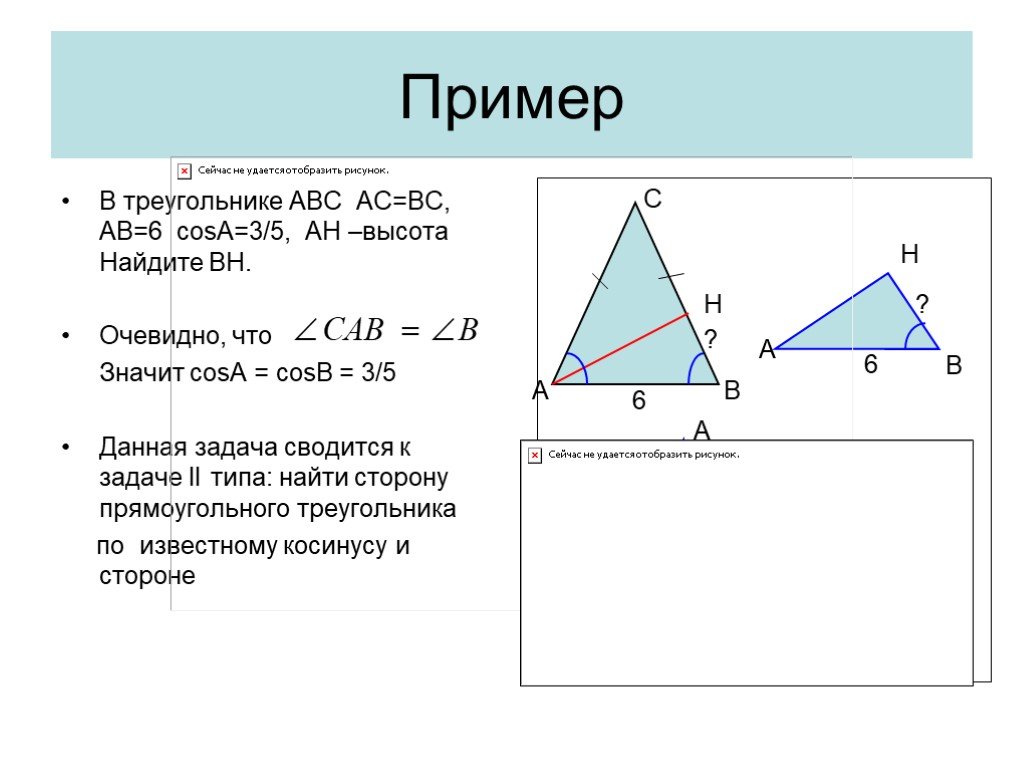
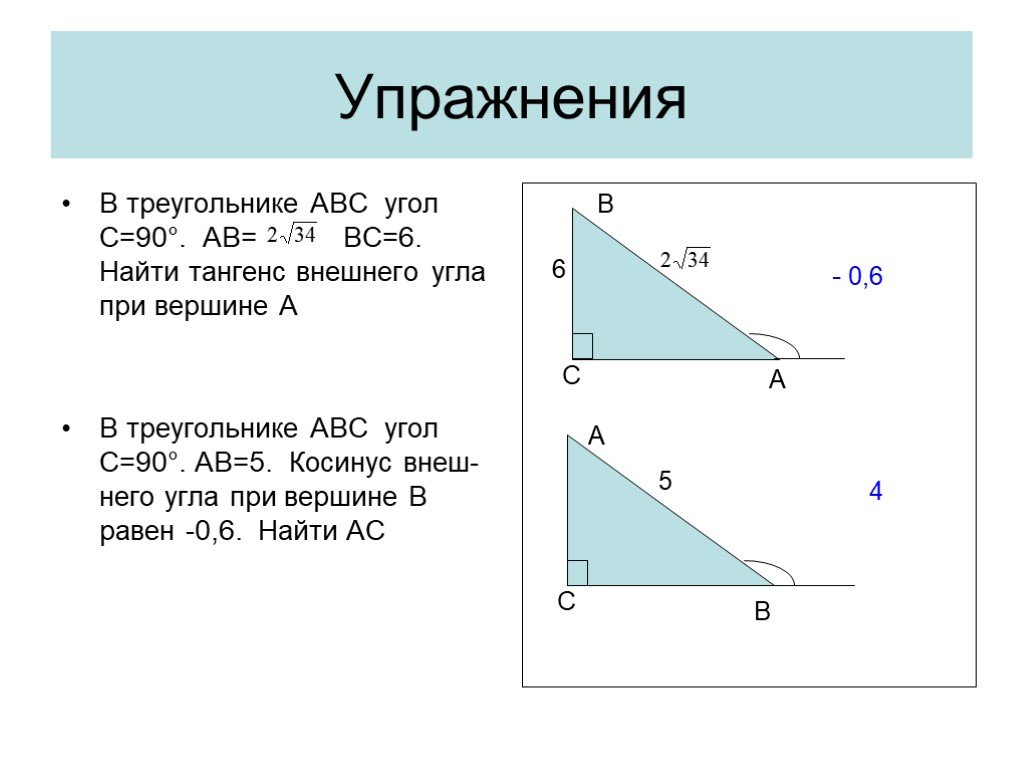
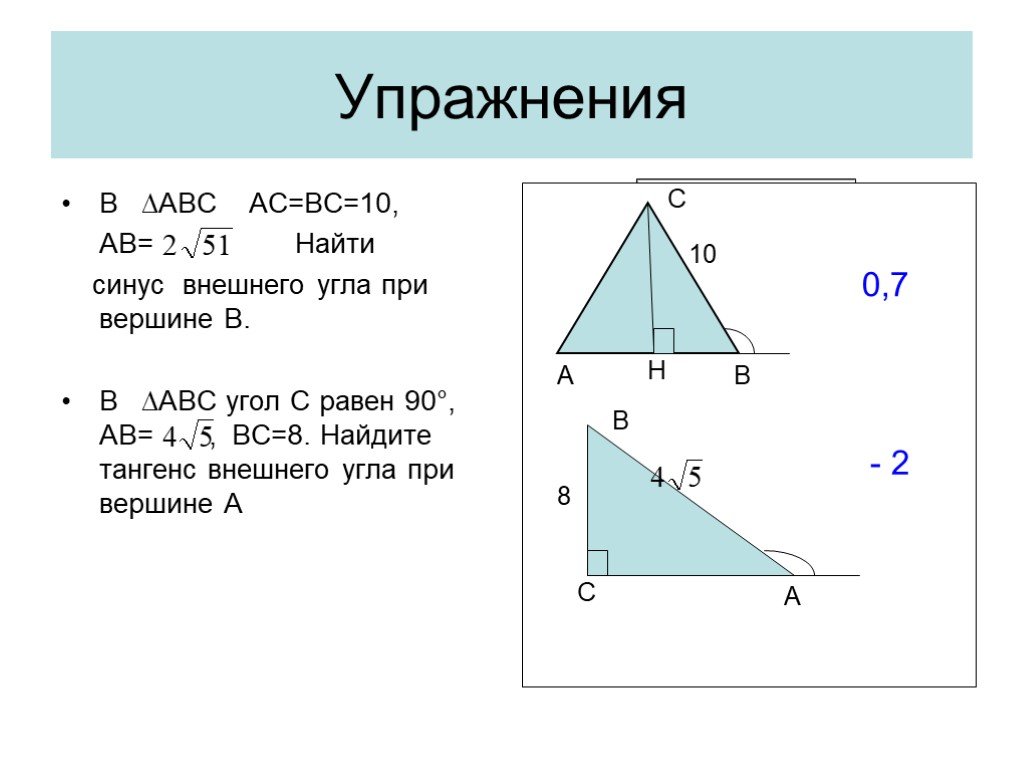
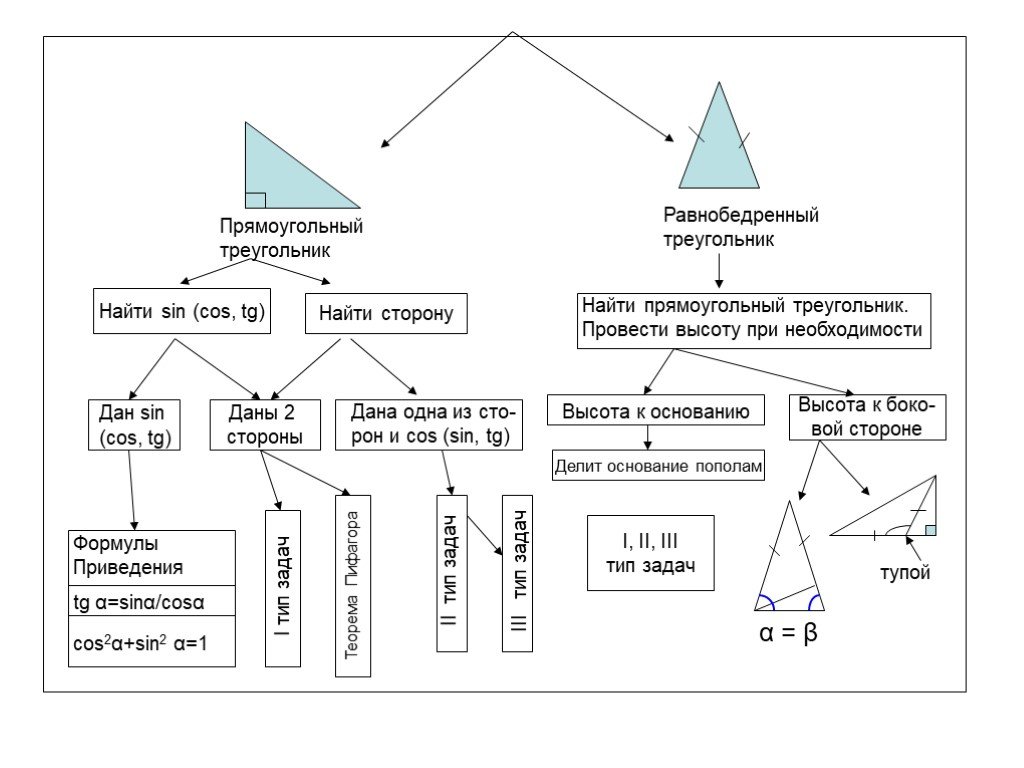
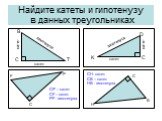
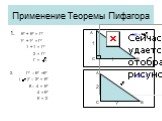
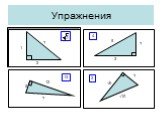
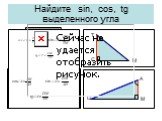
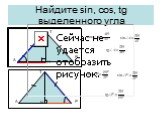
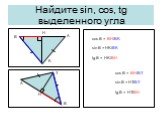
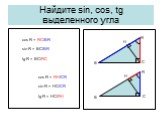
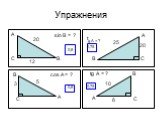
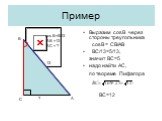
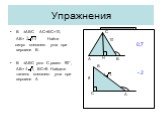
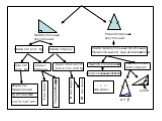
Презентация "Решение прямоугольных треугольников" по математике – проект, доклад
Презентацию на тему "Решение прямоугольных треугольников" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 66 слайд(ов).
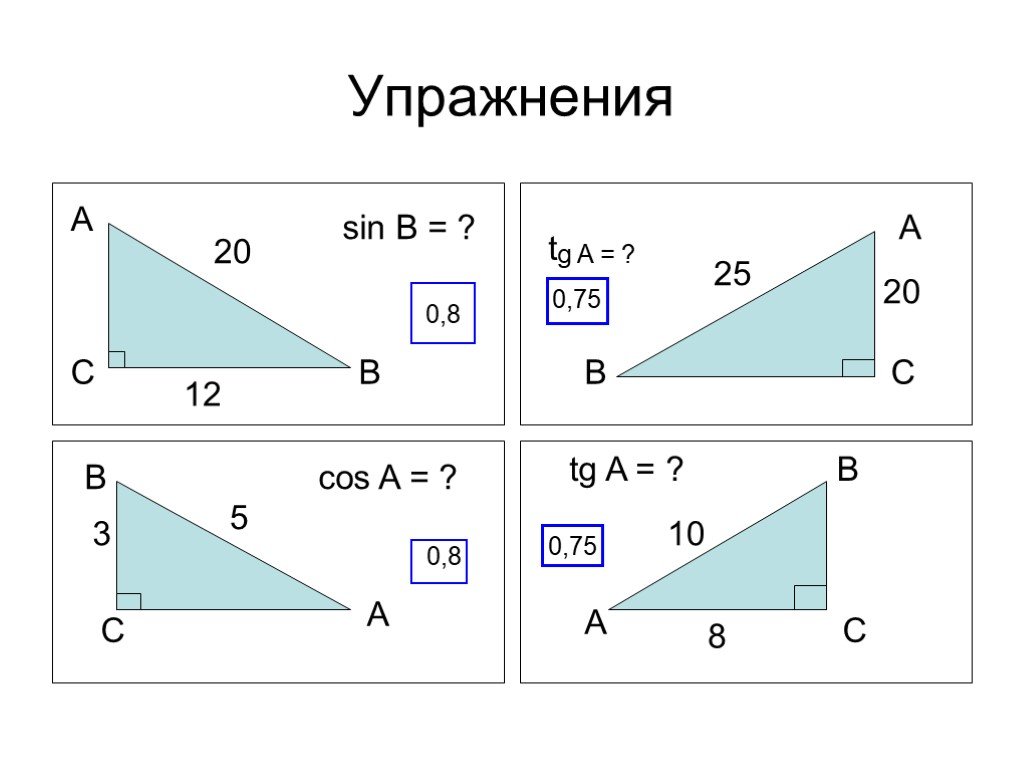
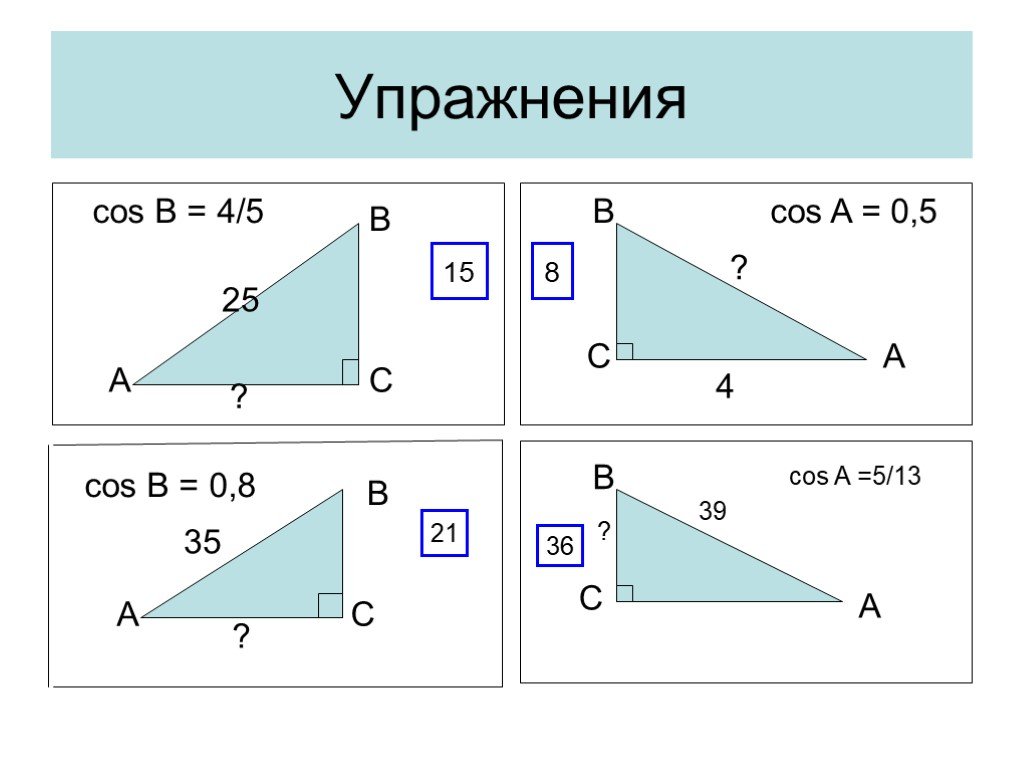
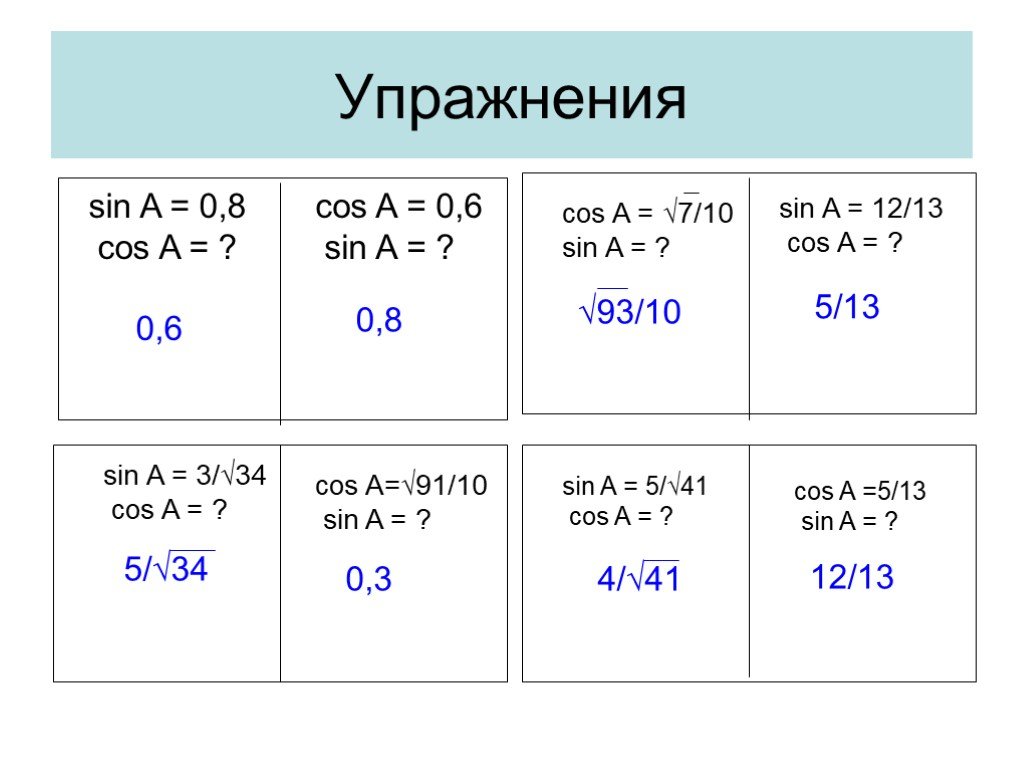
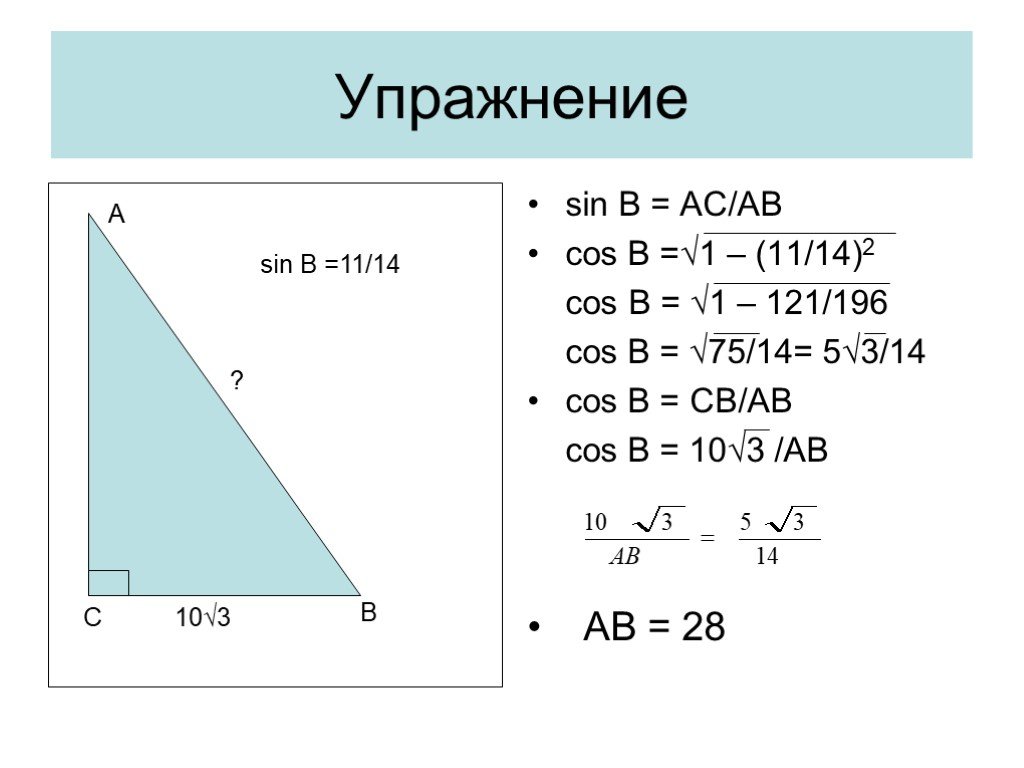
Слайды презентации
Список похожих презентаций
Решение задач на применение признаков подобия треугольников
Тема урока. Решение задач на применение признаков подобия треугольников. Цель урока: Обобщение по теме «Признаки подобия треугольников». Задачи урока:. ...Применение свойств и признаков равенства прямоугольных треугольников к решению практических задач
«Сближение теории с практикой даёт самые благотворные результаты, и не одна только практика от этого выигрывает». П.А. Чебышев. Найдите пары равных ...Решение задач на применение признаков равенства треугольников
РЕШЕНИЕ ЗАДАЧ НА ПРИМЕНЕНИЕ ПРИЗНАКОВ РАВЕНСТВА ТРЕУГОЛЬНИКОВ. ОБРАЗОВАТЕЛЬНАЯ: ЗНАТЬ ФОРМУЛИРОВКИ ПРИЗНАКОВ РАВЕНСТВА ТРЕУГОЛЬНИКОВ; ОПРЕДЕЛЕНИЕ ...Решение задач на применение первого признака равенства треугольников
Цель урока. Совершенствование навыков решения задач на применение первого признака равенства треугольников; Закрепление умения доказывать теоремы. ...Подобие треугольников решение задач
Основная цель – сформировать понятие подобных треугольников, выработать умение применять признаки подобия треугольников в процессе доказательства ...Решение задач на применение признаков подобия треугольников
Решение задач на применение признаков подобия треугольников. обобщение и систематизация теоретических знаний по теме «Признаки подобия треугольников» ...Некоторые свойства прямоугольных треугольников
ЗАДАЧИ УРОКА. РАССМОТРЕТЬ СВОЙСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ. НАУЧИТЬСЯ РЕШАТЬ ЗАДАЧИ НА ПРИМЕНЕНИЕ СВОЙСТВ ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ. СТОРОНЫ ...Некоторые свойства прямоугольных треугольников
Математический диктант. 1. Вставьте пропущенное слово:. а) Прямой угол – это угол равный … б) Сумма углов в любом треугольнике равна …. 2. Укажите ...Блиц-опрос "Решение треугольников"
Выбери вопрос. В треугольнике АВС угол А равен 40 градусов. Внешний угол при вершине В равен 68 градусов. Найдите угол С. Угол С равен 28 градусов. ...Решение задач на применение основных тригонометрических формул и преобразование выражений
Цели и задачи урока. Повторить основные тригонометрические формулы. Закрепить знания свойств синуса, косинуса, тангенса и котангенса. Научиться применять ...Решение задач на объём
B11 № 27052. Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение , которое является основанием меньшего конуса ...Решение задач 4 класса
Цели и задачи урока. развивать вычислительные навыки; совершенствовать умение решать задачи с величинами: скорость, время, расстояние; закреплять ...Решение задач В4
Прямоугольный треугольник. А В С. . . Ответ: 7. . Ответ: 2. H. Ответ: 3,75. . ...Решение диофантовых уравнений
Цели и задачи. Биография Диофанта Диофантовы уравнения с одной неизвестной Диофантовые уравнения первой степени Диофантовые уравнения высших степеней ...Решение задач
Задача 1. У Тани было 5 белых котят. 3 котика убежали. Сколько котят осталось? Решение: 5 – 3 = 2 (к.) Ответ: 2 котёнка. Задача 2. В вазе лежало 3 ...Второй и третий признаки равенства треугольников
План урока. Проверка домашнего задания. 1. Математический диктант. Объяснение нового материала. 3 Решение задач. 4. № 108. Периметр равнобедренного ...Виды треугольников по сторонам
Листок настроения. В начале урока у первого человечка нарисовать свое настроение , в конце – у второго. Сегодня, друзья, Мы отправимся в путь. Хорошее ...Второй и третий признаки подобия треугольников
докажем, что и применим 1 признак подобия треугольников.А С В В1 С1 А1.
II признак подобия треугольников. Если две стороны одного треугольника ...
Виды треугольников
ТРЕУГОЛЬНИКИ ОСТРОУГОЛЬНЫЕ ПРЯМОУГОЛЬНЫЕ ТУПОУГОЛЬНЫЕ. Треугольником называется фигура ,которая состоит из трёх точек , не лежащих на одной прямой, ...Конспекты
Некоторые свойства прямоугольных треугольников. Решение задач
Тема урока. : «Некоторые свойства прямоугольных треугольников. Решение задач». Цель:. расширить знания учащихся о прямоугольных треугольниках. ...Признаки равенства прямоугольных треугольников
Конспект урока по теме: «Признаки равенства прямоугольных треугольников», геометрия-7 класс. Тип урока: объяснение нового материала. Цели урока:. ...Признаки равенства прямоугольных треугольников
Муниципальное автономное общеобразовательное учреждение. «Средняя общеобразовательная школа № 40»,. г. Новоуральска Свердловской области. ...Некоторые свойства прямоугольных треугольников
«Некоторые свойства прямоугольных треугольников». . . Цели урока:. рассмотреть некоторые свойства прямоугольного треугольника и показать, как они ...Решение задач
МАОУ СОШ № 44. Урок . математики . во 2. классе . по . теме:. «. Решение . задач». учитель ...Решение задач
Математика. Урок-путешествие. Тема. :. Решение задач. Цель:. развивать умение решать задачи на нахождение цены, количества, стоимости; учить ...Решение дробных рациональных уравнений
8 класс. Тема « Решение дробных рациональных уравнений». Цель: закрепить изученный материал в ходе выполнения упражнений, развивать навыки решения ...Решение алгебраических уравнений
Тема: Решение алгебраических уравнений. Цели урока:. . систематизировать, обобщить, расширить знания и умения учащихся, связанные с применением ...Применение признаков равенства треугольников к решению задач
b55cb4a895045c55f93796fe95acb7c3.doc. – геометрия 7 класс. . Ладанова И.В. . . МКОУ «Верх-Жилинская ООШ». Косихинский район Алтайский край. ...Решение задач на движение
Конспект урока математики на тему:. . «Решение задач на движение» (4 класс). Автор разработки: Чепурина Т. Н., учитель начальных классов. . ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:7 января 2019
Категория:Математика
Содержит:66 слайд(ов)
Поделись с друзьями:
Скачать презентацию