Презентация "Новые признаки равенства треугольников" по математике – проект, доклад
Презентацию на тему "Новые признаки равенства треугольников" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 25 слайд(ов).
Слайды презентации
Список похожих презентаций
Второй и третий признаки равенства треугольников
План урока. Проверка домашнего задания. 1. Математический диктант. Объяснение нового материала. 3 Решение задач. 4. № 108. Периметр равнобедренного ...Признаки равенства треугольников
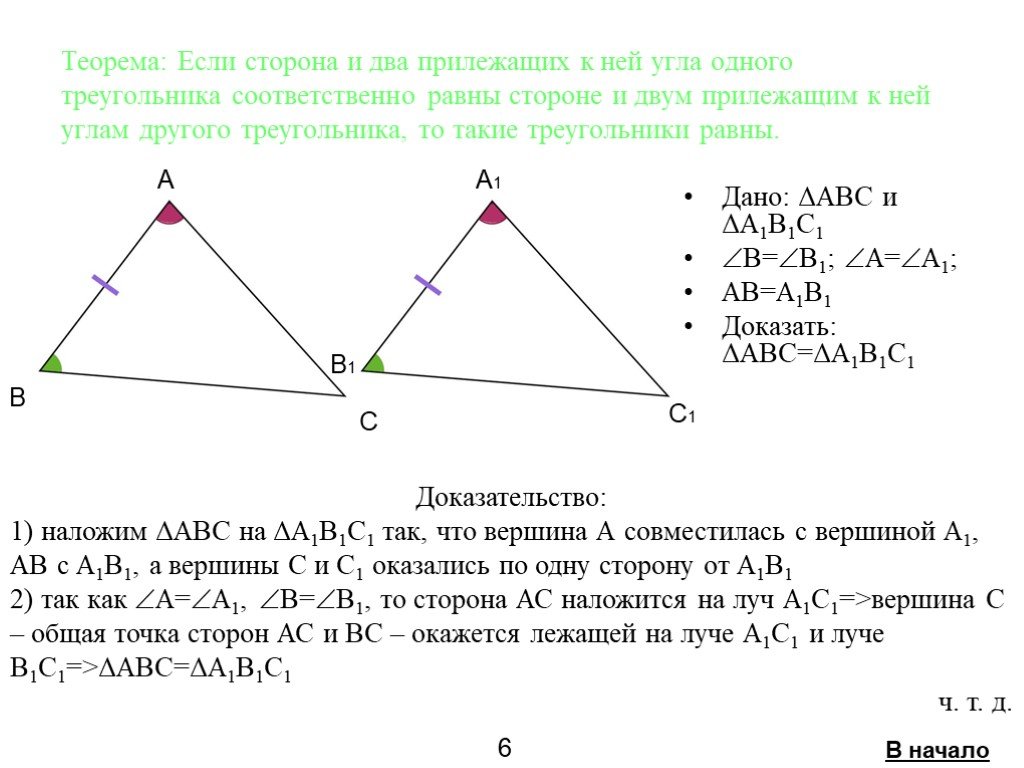
ИЛИ _______ _________ _____________. Два треугольника равны, если соответственно равны. сторона и два прилежащих к ней угла каждого треугольника. ...Признаки равенства и подобия треугольников
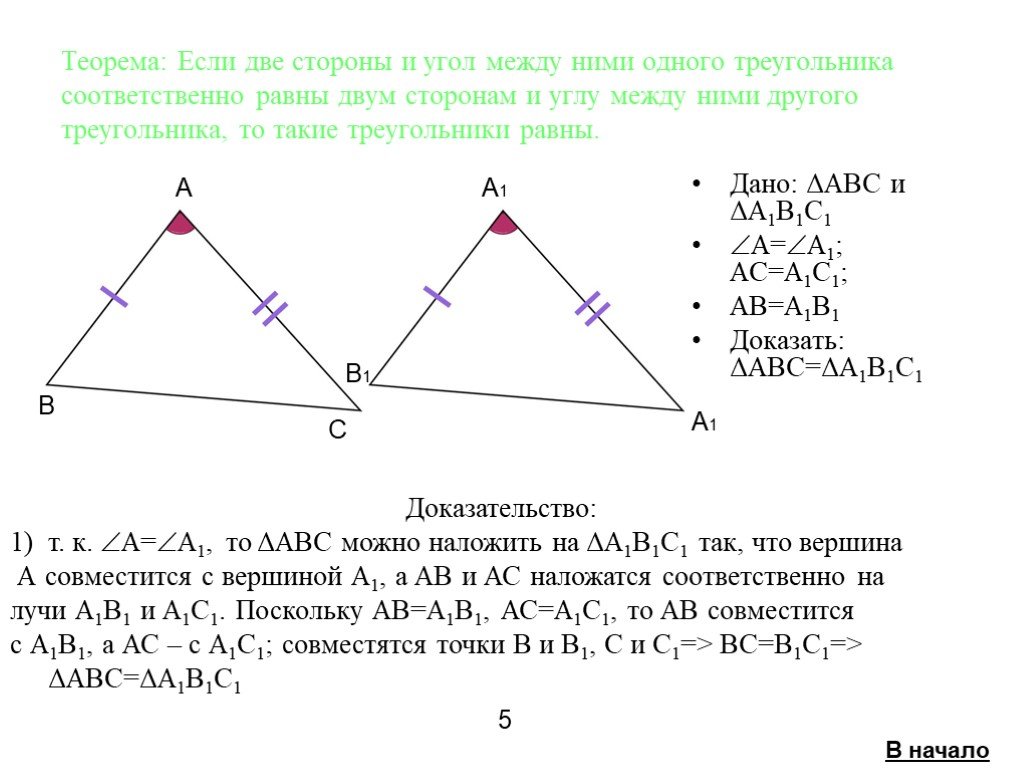
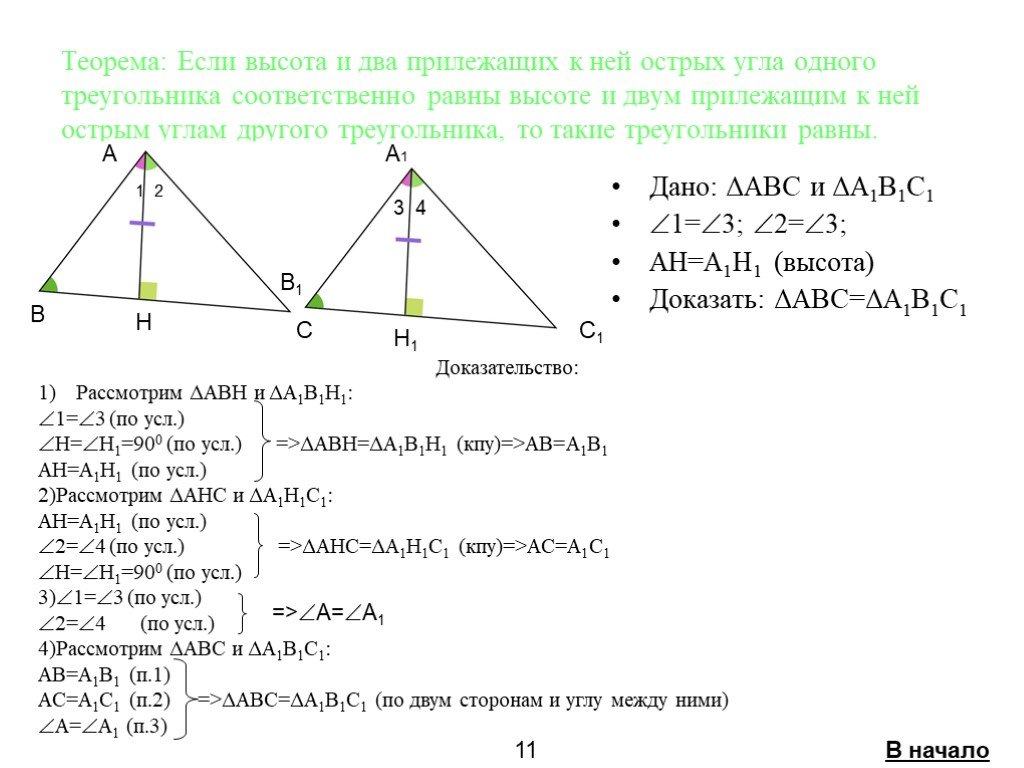
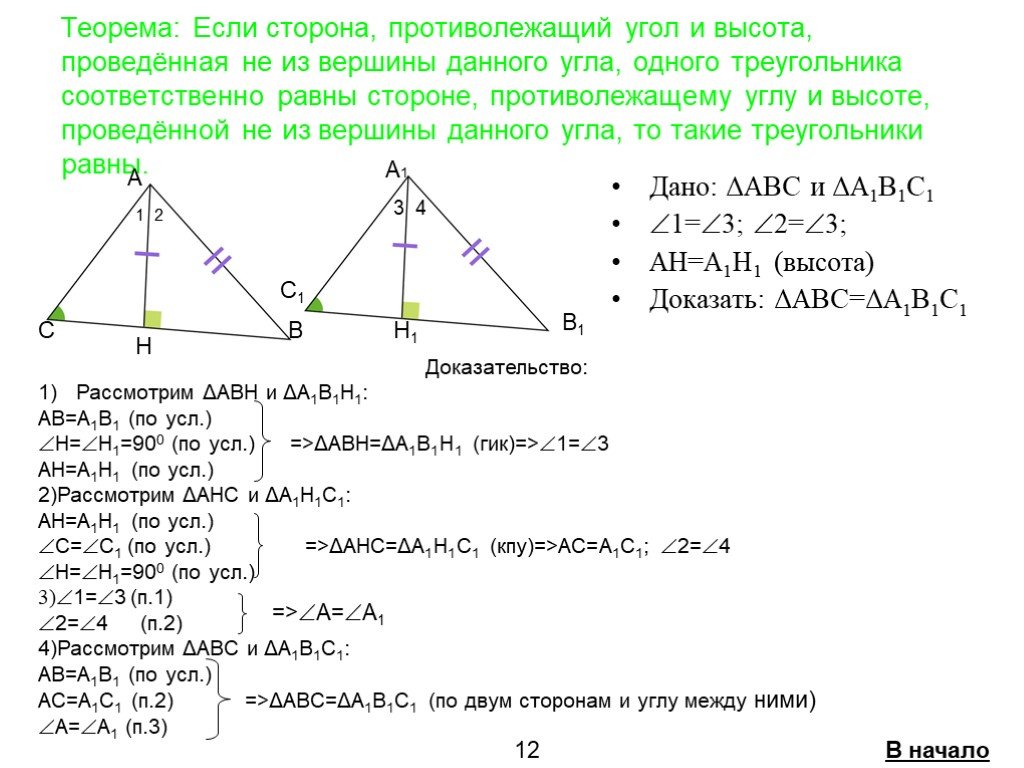
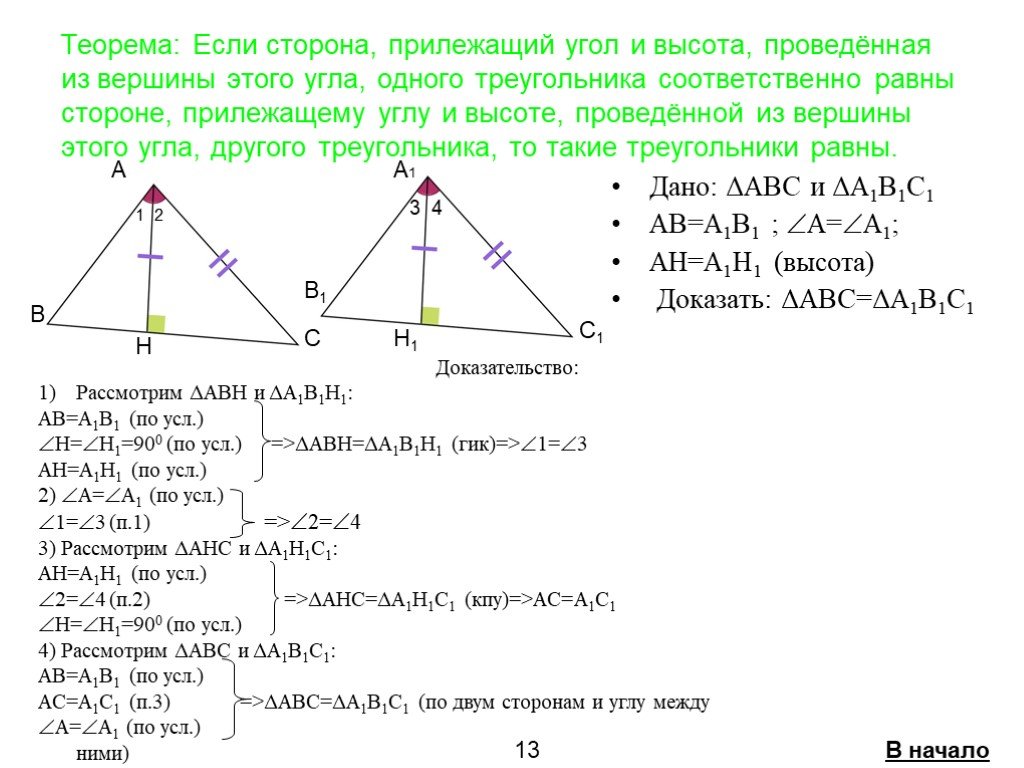
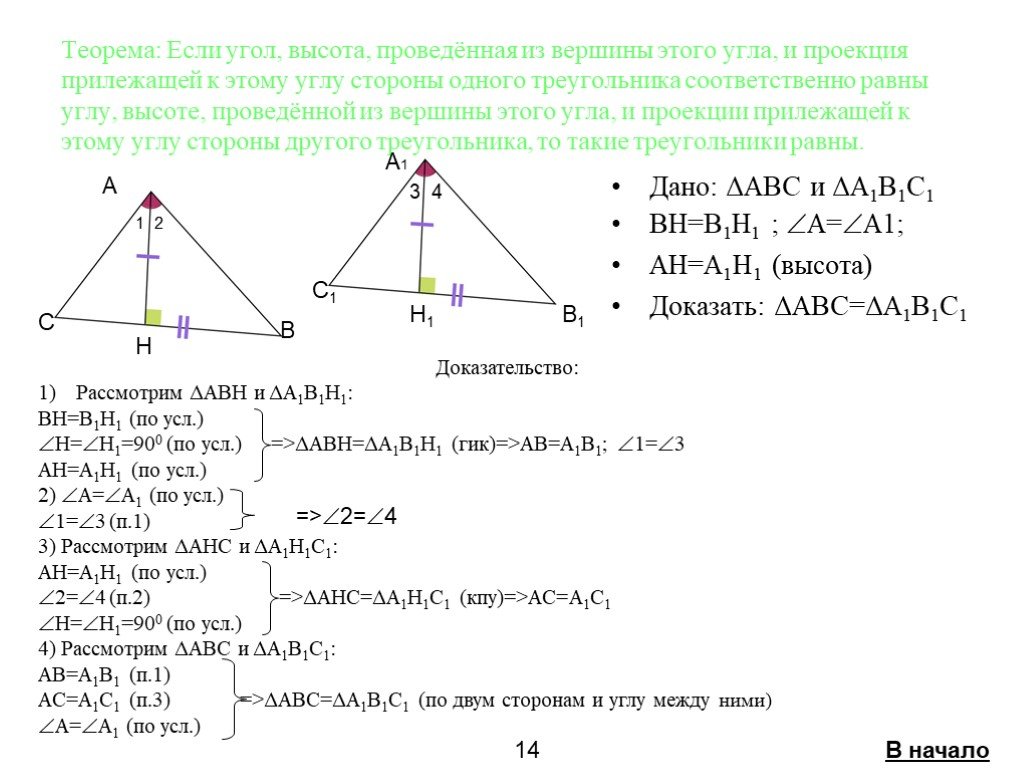
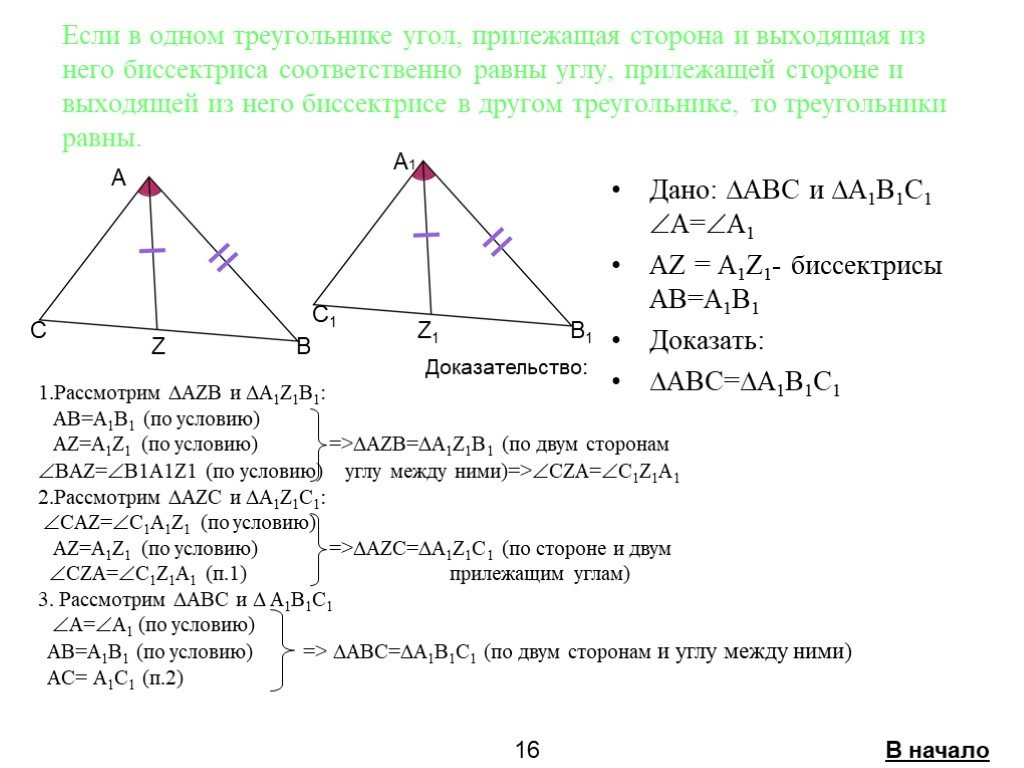
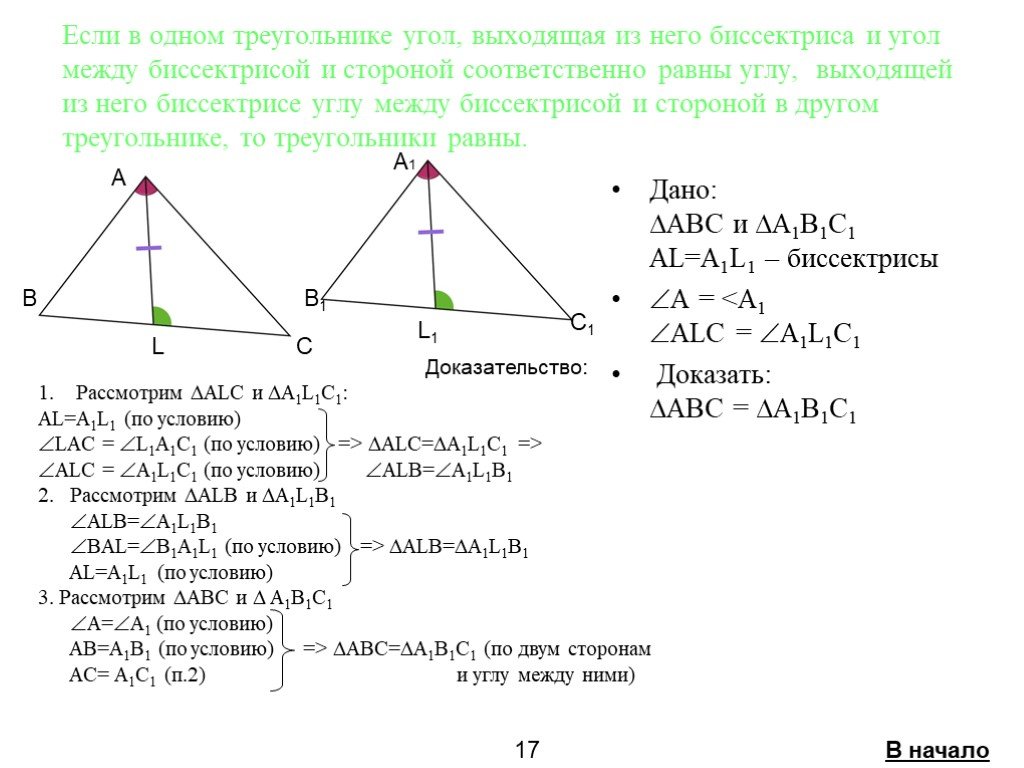
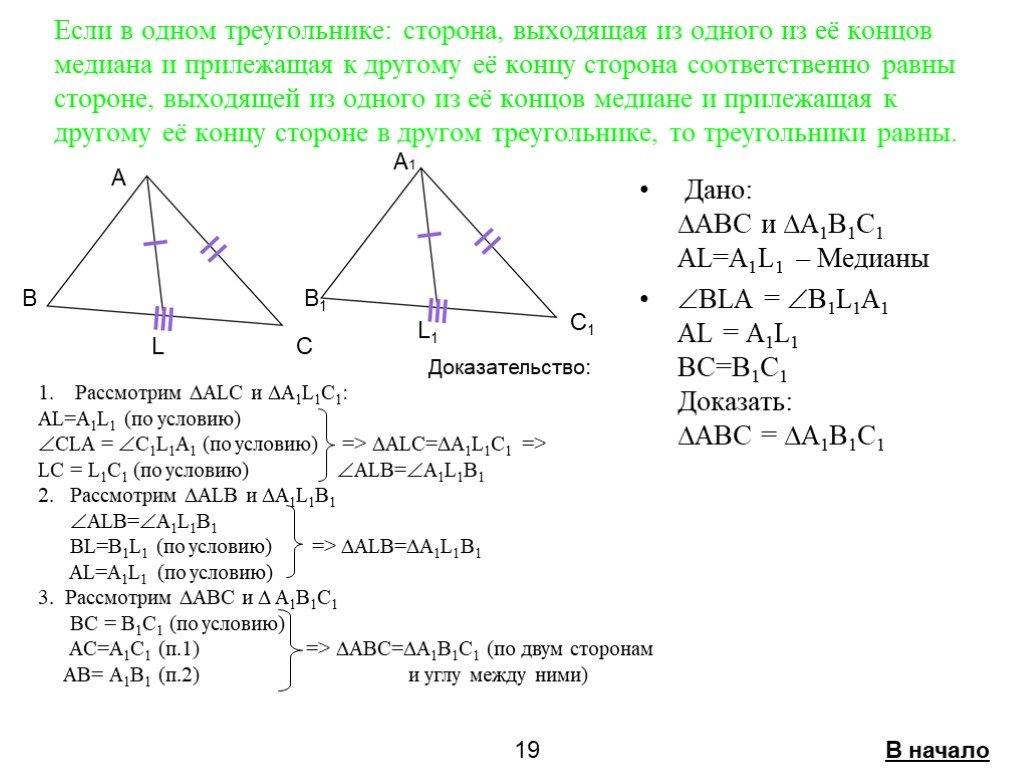
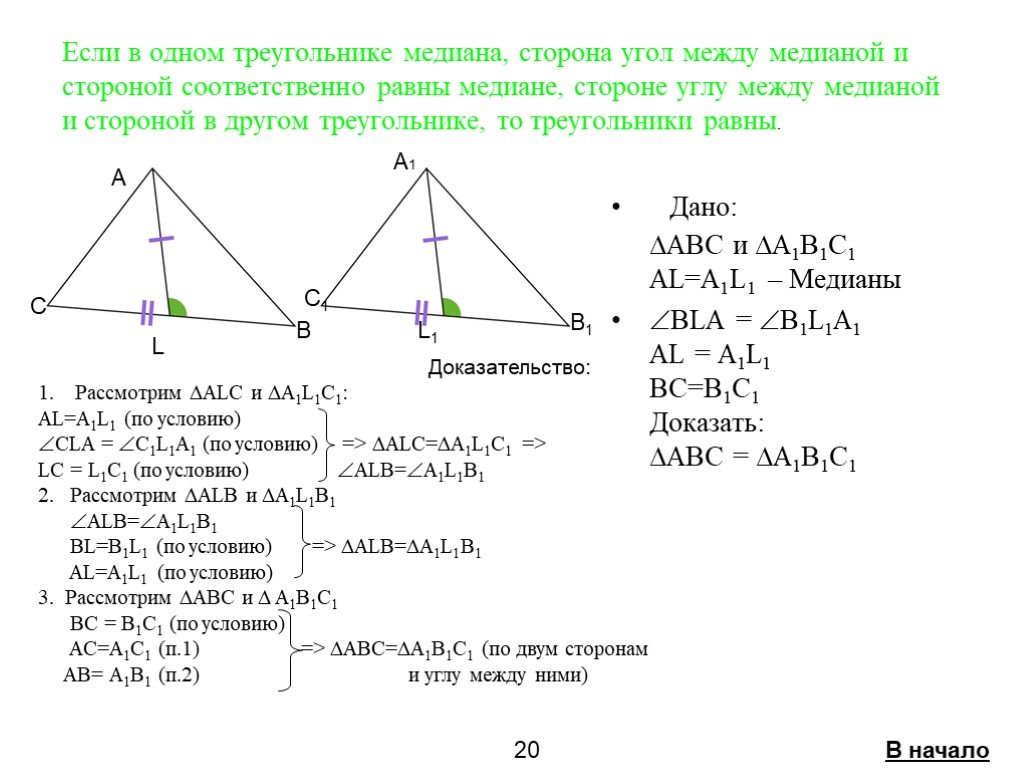
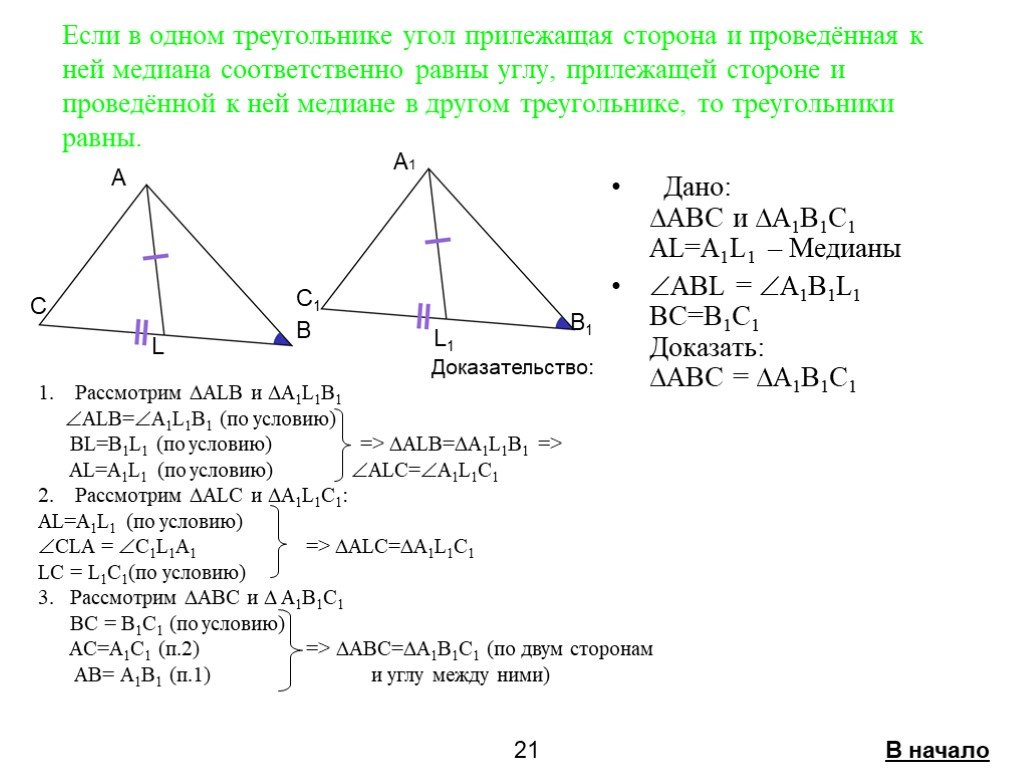
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники ...Признаки равенства треугольников
Признаки равенства треугольников. Первый признак равенства треугольников. (По двум сторонам и углу между ними ). А В С Р К М. ( по стороне и двум ...«Признаки равенства треугольников»
1.Цели и задачи занятия 2.Практическая работа 3.Таблица признаков равенства треугольников 4.Решение задач. Цели и задачи. 1. Усвоение материала через ...Признаки равенства треугольников
Игра «Молчанка» По команде учителя поднять карточку с тем цветом, напротив которого находится правильный ответ. 1)Укажите, на каком из приведённых ...Признаки равенства треугольников
Цели урока. Систематизировать и закрепить знания, умения и навыки по теме “Признаки равенства треугольников”. Равные треугольники. Треугольники называются ...Признаки равенства треугольников и свойства равнобедренного треугольника
План работы на уроке:. Признаки равенства треугольников. Свойства равнобедренного треугольника. Вопрос - ответ. 1. Какая фигура называется треугольником? ...Признаки равенства треугольников. Устные задачи
Вдохновение нужно в геометрии не меньше, чем в поэзии. А.С.Пушкин. Цель: уметь решать устные задачи на применение признаков равенства треугольников. ...Равнобедренный треугольник, признаки равенства треугольников
1. Определите, в силу какого признака равенства треугольников треугольники ABC и CDA равны, если AD = ВС, АВ = DC. 1. По двум сторонам и углу между ...Задачи на признаки подобия треугольников
- Что есть больше всего на свете? – Пространство. - Что быстрее всего? – Ум. - Что мудрее всего? – Время. - Что приятнее всего? – Достичь желаемого. ...Задачи на первый признак равенства треугольников
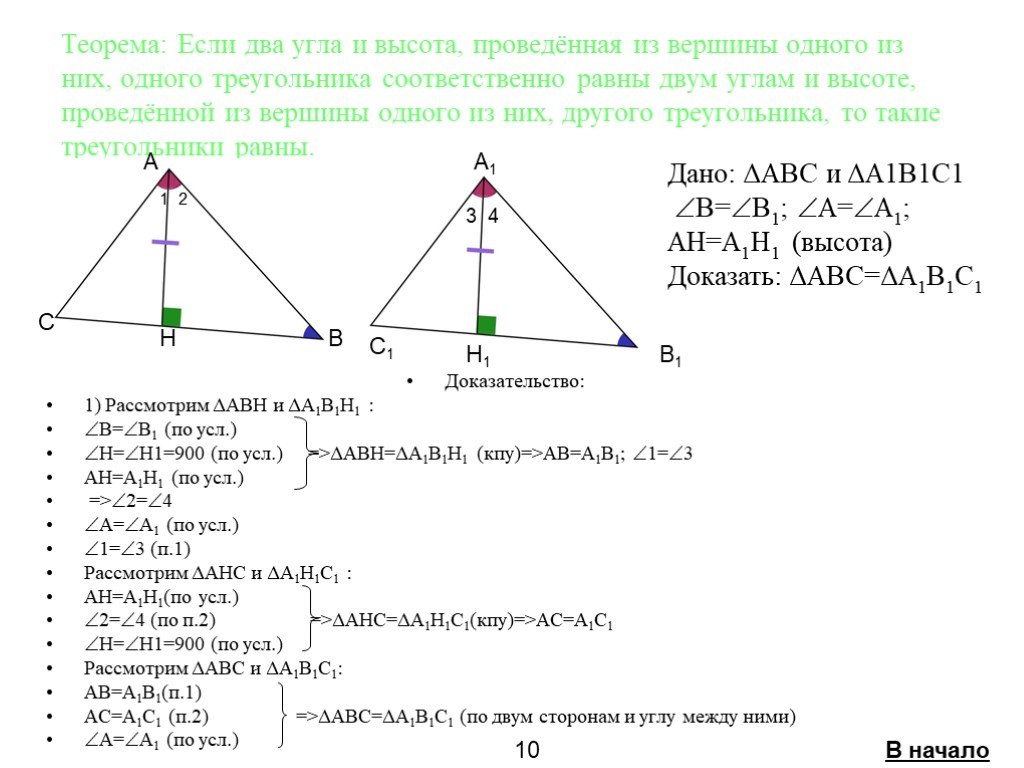
Цель урока. познакомиться с первым признаком равенства треугольников и его доказательством; научиться применять при решении задач изученные свойства ...Второй признак равенства треугольников
Решение задач по готовым чертежам. Дано: АВ = 15 см. AD = 2 дм. Найти : РАВСD. Дано: Р ACB :Р BCD :Р DCF = = 2 : 3 : 4. Найти : Р ABC. Доказать: АC ...Второй признак равенства треугольников
Решение задач по готовым чертежам с целью повторения первого признака равенства треугольников. D А В С Доказать:АС BD, BD-биссектриса ADC. 2 1. Дано: ...Второй признак равенства треугольников
Цели: изучить второй признак равенства треугольников, выработать навыки использования их при решении задач. систематизировать, расширить и углубить ...Второй признак равенства треугольников
Второй признак равенства треугольников 7 класс. Повторение:. Равенство треугольников Два треугольника называются равными, если совмещаются наложением ...Второй и третий признаки подобия треугольников
докажем, что и применим 1 признак подобия треугольников.А С В В1 С1 А1.
II признак подобия треугольников. Если две стороны одного треугольника ...
1 признак равенства треугольников
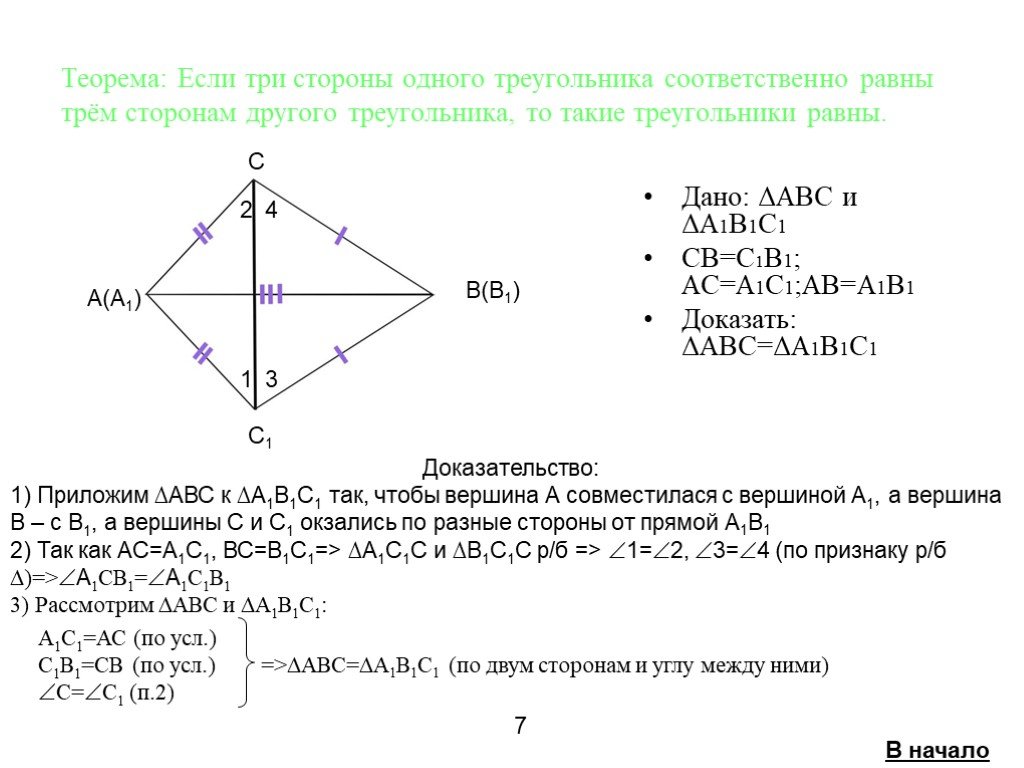
Цели урока:. ввести понятие теоремы и доказательства теоремы; доказать первый признак равенства треугольников; научиться решать задачи на первый признак ...Третий признак равенства треугольников
Цели: изучить третий признак равенства треугольников, выработать навыки использования их при решении задач. систематизировать, расширить и углубить ...Конспекты
Признаки равенства прямоугольных треугольников
Муниципальное автономное общеобразовательное учреждение. «Средняя общеобразовательная школа № 40»,. г. Новоуральска Свердловской области. ...Признаки равенства треугольников
Цель урока. : обобщить и закрепить знания учащихся по теме: «Признаки равенства треугольников». Тип урока. : урок обобщения. Оборудование:. карточки ...Признаки равенства треугольников
Конспект урока по геометрии в 7 классе по проектной технологии. Тема: « Признаки равенства треугольников.». Цель урока: Обучающая:. - закрепить ...Признаки равенства треугольников
. . . . . . . . . . Никифорова Марина Николаевна. . учитель математики. . . Государственное бюджетное образовательное ...Признаки равенства треугольников
10. . Урок математики с применением. блочно-модульного обучения. . в современной школе. Признаки равенства треугольников. 7 класс. Урок-лекция ...Равенство треугольников. Признаки равенства треугольников
урок. Учитель:. Нурмуханбетова Г.С. Предмет:. геометрия. Класс. : 7 «Г». Дата: 15.01.2015. Тема. :. Равенство треугольников. Признаки равенства ...Решение задач. Признаки равенства треугольников
Гуранская Г.В. учитель математики и информатики СШ№3 им.П.И.Морозова г.Щучинска. . Тема урока. . Решение задач. Признаки равенства треугольников. ...Треугольники. Признаки равенства треугольников
РАЗРАБОТКА УРОКА по геометрии 7 класс: « Треугольники. Признаки равенства треугольников». Выполнила учитель 2 категории Петракова Е.Н.(Саратовская ...Признаки равенства прямоугольных треугольников
Конспект урока по теме: «Признаки равенства прямоугольных треугольников», геометрия-7 класс. Тип урока: объяснение нового материала. Цели урока:. ...Треугольники. Признаки равенства треугольников
Конспект урока геометрии для 7 класса на тему. « Треугольники. . . Признаки равенства треугольников». ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:11 декабря 2018
Категория:Математика
Содержит:25 слайд(ов)
Поделись с друзьями:
Скачать презентацию