Презентация "Теория и практика решения задания 18 ЕГЭ по информатике" – проект, доклад
Презентацию на тему "Теория и практика решения задания 18 ЕГЭ по информатике" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Информатика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 79 слайд(ов).
Слайды презентации
Список похожих презентаций
ЕГЭ по информатике
Структура экзаменационной работы. Общее число заданий в экзаменационной работе – 32. Общее время выполнения работы – 240 мин. Экзаменационная работа ...Задания по информатике
Лес Поляна Чаща. Самый синий цветок. Самая глубокая нора. Самая высокая сосна. Дом Эльфа Дом Хмурика Дом Шишкоеда. Адрес Эльфа: Лес, Поляна, Самый ...ЕГЭ-2017 по информатике "Задание 11. Рекурсивные алгоритмы"
Теория Рекурсия вокруг нас Рекурсия в математике Программирование Задачи на закрепление Список использованной литературы. Содержание. Реку́рсия (RECURCIО ...Анализ ресурсов по подготовке учащихся к ЕГЭ по информатике
Технопарк в сфере высоких технологий “Жигулёвская долина" областная целевая программа на 2010-2014 годы. Приоритетными направлениями специализации ...ЕГЭ по информатике
Основы логики. Знание символики Знание таблиц истинности основных логических операций (инверсия, конъюнкция, дизъюнкция), а также импликации Знание ...Графический способ решения систем уравнений
Образовательные: Выработать умение самостоятельно применять знания в комплексе, переносить их в новые условия, в том числе работать с электронной ...Викторина по Информатике "Угадайка"
ПОПРОБУЙ ПРОЧИТАЙ! Слова зашифрованы с использованием: команд ОС расширений файлов операторов языков программирования названий клавиш служебных слов. ...Викторина по информатике
4 3 1 10 19 18 17 16 15 14 13 11 9 8 7 6 5 0 30. Что означает слово "компьютер”? Вычислитель Умножитель Мыслитель. В результате компьютерного сбоя ...Архитектурные решения построения ИСУ
ИСУ. Архитектурные решения построения ИСУ Распределенная система. В настоящее время практически все большие программные системы являются распределенными. ...Анимированные ребусы по информатике
пере да ча обра бот ка. т очк а па мят ь. комп тер ью. кла виа тура. проце с со р кур сор. ок но шаб лон. мод ем ката лог. алг о ри тм арх ива ция. ...Альманах интерактивных презентаций-тестов анаграмм по информатике и ИТ
Анаграмма: Кто есть who? Анаграмма - это слово, образованное путем перестановки букв исходного слова, например, ИГОЛКА = ЛОГИКА. В заданиях используются ...Адресация в Интернет. Подготовка к ЕГЭ
Компьютерные сети. Адресация в Интернете. каждый компьютер, подключенный к сети Интернет, должен иметь собственный адрес, который называют IP-адресом ...Задачи на кодирование текстовой информации и определение объема методика решения задач повышенного уровня сложности
Что следует знать:. чаще всего используют кодировки, в которых на символ отводится 8 бит (8-битные) или 16 бит (16-битные) необходимо запомнить, что ...Исполнители в ЕГЭ
Уметь размышлять и анализировать Уметь выполнять алгоритмы в среде формального Исполнителя алгоритмов. Необходимые знания и умения. 2004-2005 год ...Игры по информатике
Что такое информация? Назовите виды алгоритмических структур. Раскодируйте сообщение. Что такое информатика? Разветвляющися алгоритм.... (продолжите ..."Своя игра" по информатике
Вопросы Финал. Что изучает информатика? Способы представления, накопления (хранения), обработки информации с помощью технических средств. Что такое ...Игра-конкурс по информатике
Цель:. Формировать у учащихся общеучебные навыки: постановка цели, разработка алгоритма, умение обосновать решение; Развивать логические способности ...Игра по информатике
Первый этап. 1. Какая величина измеряется в МГц? 1) скорость доступа к требуемому месту на диске для чтения или записи информации; 2) скорость доступа ...Игра по информатике "Счастливый случай"
1 гейм – «Дальше, дальше…» 2 гейм – «Заморочки из бочки» 3 гейм – «Веришь – не веришь» 4 гейм – «Всё наоборот» 5 гейм – «Конкурс капитанов». План ...Конспекты
Использование элементов алгебры логики при решении заданий ЕГЭ по информатике
Муниципальное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа № 2 п. Мостовского. муниципального образования Мостовский ...Нестандартное занятие - КВН по информатике для обучающихся четвертого года обучения
МБОУ ДОД « центр творческого развития и гуманитарного образования». Конспект занятия по информатике. на тему:. Нестандартное ...Загадки по информатике
Конспект урока на тему «Загадки по информатике». Скромный серый колобок,. Длинный тонкий проводок,. Ну а на коробке -. Две или три кнопки. . ...Графический способ решения систем уравнений с 2-мя переменными средствами Microsoft Excel
Урок по теме:. «Графический способ решения систем уравнений с 2-мя переменными средствами. Microsoft. . Excel. ». Класс: 9. . . Кол-во часов: ...Лучший по профессии
Муниципальное образование Ленинградский район. Муниципальное автономное образовательное учреждение для детей. межшкольный учебный комбинат. ...Лабораторная работа №3 Симплекс – метод решения задач. ПК №3
Колледж АО «Финансовая академия». Разработка открытого урока. Тема: «Лабораторная работа №3 Симплекс – метод решения задач. ...Контрольная работа по PowerPoint
Суворова Галина Викторовна. . Суворова Галина Викторовна. . КГУ «Школа-гимназия города Курчатова», Казахстан, ВКО, город Курчатов. . ...Компьютерная графика. Виды компьютерной графики. Программы по созданию и обработке векторной и растровой графики, форматы графических файлов
Коммунальное государственное учреждение. «Рудная средняя школа». учитель информатики. Сатиева Светлана Маратовна. Тема: Компьютерная графика. ...Итоговая работа по базам данных
Тема: Итоговая работа по базам данных. Цели:. дидактические:. . . создать условия для проверки уровня знаний;. . контроль, самоконтроль ...Вводный урок по Exсel
Информатика. Класс:. 9. . Тема:. «Вводный урок. по Ex. сel. ». Тип урока: комбинированный. Методы:. словесный (рассказ, беседа, объяснение) ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:1 июня 2019
Категория:Информатика
Содержит:79 слайд(ов)
Поделись с друзьями:
Скачать презентацию












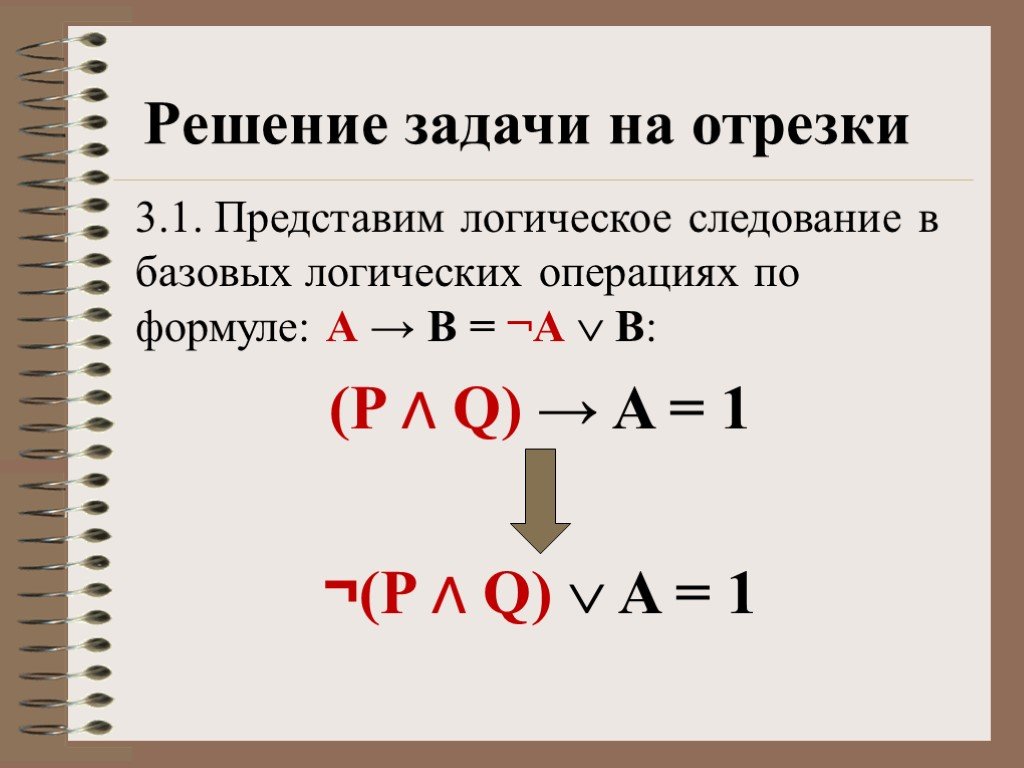







































































![Задания на отрезки. (№ 376) На числовой прямой даны два отрезка: P=[4,15] и Q=[12,20]. Укажите наименьшую возможную длину такого отрезка A, что формула ((x ∈ P) ∧ (x ∈ Q)) → (x ∈ A) тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Источник - сайт Полякова К.Ю. Задания на отрезки. (№ 376) На числовой прямой даны два отрезка: P=[4,15] и Q=[12,20]. Укажите наименьшую возможную длину такого отрезка A, что формула ((x ∈ P) ∧ (x ∈ Q)) → (x ∈ A) тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Источник - сайт Полякова К.Ю.](https://prezentacii.org/upload/cloud/19/06/46965/images/thumbs/screen6.jpg)








![Пересечение отрезков P и Q можно визуализировать: P=[4,15] и Q=[12,20]. 4 12 20. По условию нашей задачи, нам нужна минимальная длина отрезка А. Находим ее: 15 – 12 = 3. Ответ: 3. Ответ на сайте Полякова К.Ю.: 3 Пересечение отрезков P и Q можно визуализировать: P=[4,15] и Q=[12,20]. 4 12 20. По условию нашей задачи, нам нужна минимальная длина отрезка А. Находим ее: 15 – 12 = 3. Ответ: 3. Ответ на сайте Полякова К.Ю.: 3](https://prezentacii.org/upload/cloud/19/06/46965/images/thumbs/screen15.jpg)
![(№ 360) На числовой прямой даны три отрезка: P=[10,25], Q=[15,30] и R=[25,40]. Какова максимальная длина отрезка A, при котором формула ((x ∈ Q) → (x ∉ R) ) ∧ (x ∈ A) ∧ (x ∉ P) тождественно ложна, то есть принимает значение 0 при любом значении переменной х? Источник - сайт Полякова К.Ю. (№ 360) На числовой прямой даны три отрезка: P=[10,25], Q=[15,30] и R=[25,40]. Какова максимальная длина отрезка A, при котором формула ((x ∈ Q) → (x ∉ R) ) ∧ (x ∈ A) ∧ (x ∉ P) тождественно ложна, то есть принимает значение 0 при любом значении переменной х? Источник - сайт Полякова К.Ю.](https://prezentacii.org/upload/cloud/19/06/46965/images/thumbs/screen16.jpg)









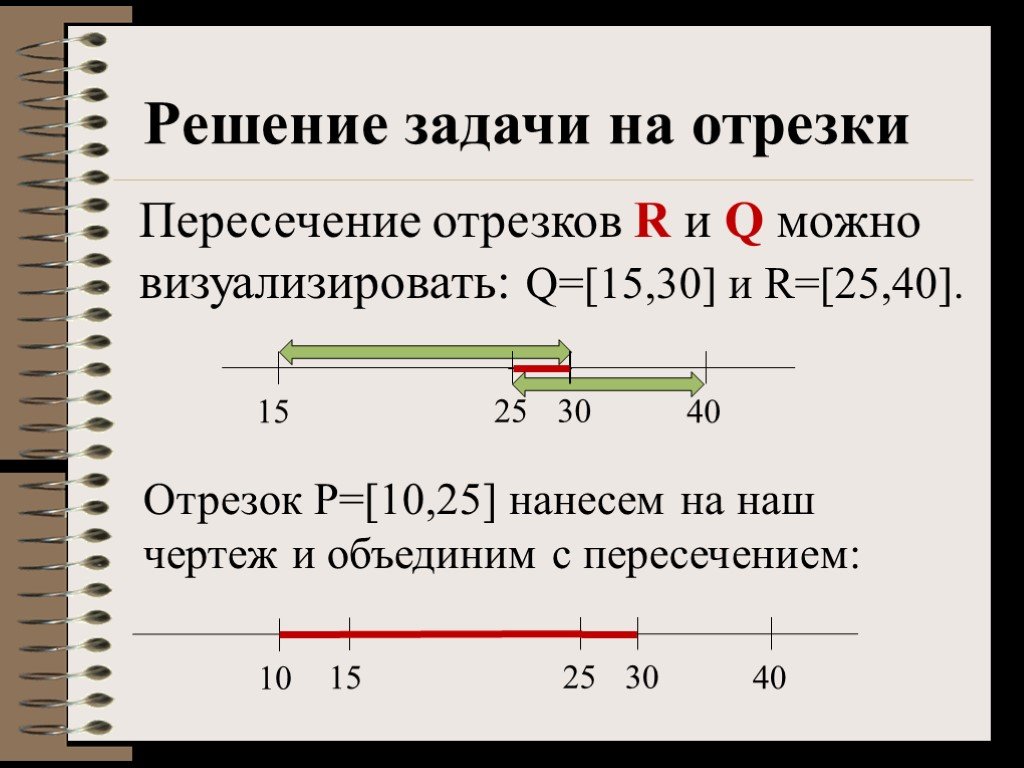
![Пересечение отрезков R и Q можно визуализировать: Q=[15,30] и R=[25,40]. Отрезок P=[10,25] нанесем на наш чертеж и объединим с пересечением: 10 Пересечение отрезков R и Q можно визуализировать: Q=[15,30] и R=[25,40]. Отрезок P=[10,25] нанесем на наш чертеж и объединим с пересечением: 10](https://prezentacii.org/upload/cloud/19/06/46965/images/thumbs/screen26.jpg)



















































































