ЕГЭ-2017 по информатике "Задание 11. Рекурсивные алгоритмы" презентация, проект, доклад

Рекурсивные алгоритмы

ЕГЭ-2017 по информатике. Задание 11

Автор: Фоминова Елена Владимировна, учитель физики и информатики МБОУ СОШ № 23 МО Усть-Лабинский район хутора Братского Краснодарского края

Теория Рекурсия вокруг нас Рекурсия в математике Программирование Задачи на закрепление Список использованной литературы

Содержание

Реку́рсия (RECURCIО - возвращение) — определение, описание, изображение какого-либо объекта или процесса внутри самого этого объекта или процесса, то есть ситуация, когда объект является частью самого себя.

Теория

Рекурсивным называется любой объект, который частично определяется через себя.

Что нужно знать: Рекурсия может быть прямой и косвенной. Рекурсия – это приём, позволяющий свести исходную задачу к одной или нескольким более простым задачам того же типа. Чтобы определить рекурсию, нужно задать: -условие остановки рекурсии -рекуррентную формулу Любую рекурсивную процедуру можно запрограммировать с помощью цикла Рекурсия позволяет заменить цикл и в некоторых сложных задачах делает решение более понятным, хотя часто менее эффективным.

Рекурсия может быть прямой и косвенной. В случае прямой рекурсии вызов функцией самой себя делается непосредственно в этой же функции procedure F(n: integer); begin writeln(n); if n > 1 then begin F(n-1); F(n-3) end end; end;

Косвенная рекурсия создаётся за счёт вызова данной функции из какой-либо другой функции, которая сама вызывалась из данной функции. function F(n: integer): integer; begin if n > 2 then F := F(n - 1) + G(n - 2) else F := 1; end; function G(n: integer): integer; begin if n > 2 then G := G(n - 1) + F(n - 2) else G := 1; end;

Уроборос – змей, кусающий свой собственный хвост. Это древний символ бесконечности Вселенной и времени, круговорота жизни, отождествляемых с рекурсией.

Рекурсия вокруг нас…

Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из затухающих отражений зеркал.

Классическим примером конечной рекурсии является русская матрешка.

Рассказ из С.Лева «Кибериады» о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей. (бесконечная рекурсия - каждая новая машина строила себе подобную).

Н.В. Гоголь в повести «Портрет» описывает сон художника Черткова (сон третьего уровня рекурсии). Проснувшись от этого сна Чертков попадает на второй уровень рекурсии – во второй сон. Проснувшись от второго сна, он попадает в первый сон, от которого тоже придется проснуться.

"Мастер и Маргарита" - один из наиболее ярких рекурсивных романов. Тема Иешуа и Пилата рекурсивно вызывается из темы Мастера и Маргариты. Кроме того, здесь так же используется прием "книга в книге". Мастер пишет роман об Иешуа и Пилате, текст которого сливается с текстом книги "Мастер и Маргарита".

Первым романом, удивившим читателей приемом рекурсии, был "Дон Кихот". Сервантес все время пытался смешивать два мира: мир читателя и мир книги. У Сервантеса главный процесс не просто книга, но книга плюс читатель. В шестой главе цирюльник, осматривая библиотеку Дон Кихота, находит книгу Сервантеса и высказывает суждения о писателе. Вымысел Сервантеса рассуждает о нем. В начале девятой главы сообщается, что роман переведен с арабского и что Сервантес купил его на рынке. Наконец, во второй части романа персонажи уже прочли первую часть.

Элементы использования рекурсии находим еще раньше у Шекспира. Гамлет ставит спектакль, где в упрощенном варианте описываются события трагедии.

В романее Л. Толстого «Война и мир» рекурсия отражает прошлое в настоящем и будущем.

У попа была собака, он её любил Она съела кусок мяса, он её убил В землю закопал, Надпись написал: «У попа была собака, он её любил Она съела кусок мяса, он её убил В землю закопал, Надпись написал:

Р. Бернс «Дом, который построил Джек» в переводе С. Маршака Вот дом, Который построил Джек. А это пшеница, Которая в темном чулане хранится В доме,  Который построил Джек А это веселая птица-синица, Которая часто ворует пшеницу,  Которая в темном чулане хранится.

А. Блока Ночь, улица, фонарь, аптека. Бессмысленный и тусклый свет. Живи еще хоть четверть века –  Все будет так. Исхода нет. Умрешь – начнешь опять сначала, И повторится все, как встарь: Ночь, ледяная рябь канала, Аптека, улица, фонарь.

Мориса Эшера «Рисующие руки»

Мориса Эшера «Галерея гравюр»

Фрактал "Треугольник Серпинского"

Эйфелева Башня в Париже

Исторический музей в Москве

Дерево состоит из веток. Ветка в свою очередь состоит из более маленьких веточек. Каждая ветка повторяет дерево. Реки образуются из впадающих в них рек. Чешуя шишек и семена некоторых цветов (например, подсолнечника) расположены пересекающимися спиралевидными веерами, определяемыми соотношением чисел Фибоначчи.

Эффект Дросте - термин для изображения специфического вида рекурсивного изображения. Изображение включает уменьшенный собственный вариант самого себя. Этот более малый вариант после этого показывает даже более малый вариант себя, и так далее. Практически это продолжается пока разрешение изображения позволяет уменьшает размер. Термин был введен в честь Дросте, голландского какао.

Герб Российской Федерации является рекурсивно-определённым графическим объектом: в правой лапе изображённого на нём двуглавого орла зажат скипетр, который венчается уменьшенной копией герба. Так как на этом гербе в правой лапе орла также находится скипетр, получается бесконечная рекурсия.

Рекурсия в математике

1) Арифметическая прогрессия: а)а1=а0; б) аn=аn-1+d. 2) Геометрическая прогрессия: а) а1=а0; б) аn=а n-1*q.

3) Факториал an=n! n!=1*2*3*4*5*б*...*n. а)а1=1; б) аn=n*аn-1. 4) Числа Фибоначчи. x1=x2=1 xn=xn-1+xn-2 при n > 2 Каждый элемент ряда Фибоначчи является суммой двух предшествующих элементов, т.е. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…

Программирование

Рекурсия — это такой способ организации вспомогательного алгоритма (подпрограммы), при котором эта подпрограмма (процедура или функция) в ходе выполнения ее операторов обращается сама к себе.

В программировании рекурсия — вызов функции из неё же самой, непосредственно или через другие функции, например, функция A вызывает функцию B, а функция B — функцию A. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.

В языке программирования Pascal рекурсивностью могут обладать как функции, так и процедуры. Примеры рекурсивной процедуры. Общая форма записи: Procedure Rec (a:integer); Begin If a>0 Then Rec(a-1); Writeln(a); End;

Важно!

Выполнение рекурсивного алгоритма можно представить следующим образом: каждый рекурсивный вызов процедуры F порождает в памяти компьютера новую копию этой процедуры и запускает ее на выполнение со своими значениями входных параметров. После того как процедура F завершила работу, выполнение программы продолжается со следующего оператора после вызова F.

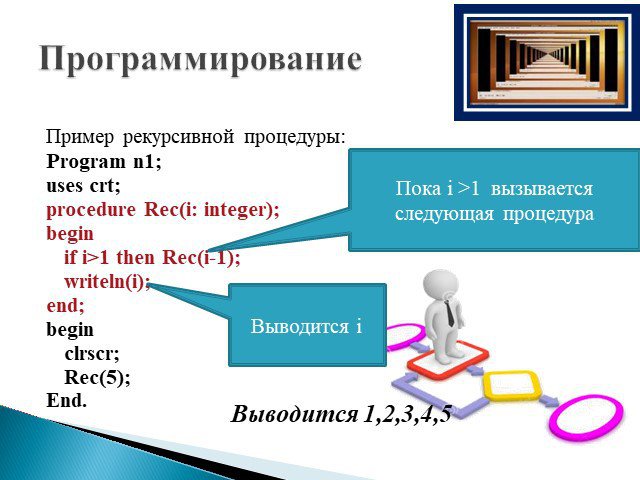
Пример рекурсивной процедуры: Program n1; uses crt; procedure Rec(i: integer); begin if i>1 then Rec(i-1); writeln(i); end; begin clrscr; Rec(5); End.

Выводится 1,2,3,4,5

Пока i >1 вызывается следующая процедура

Выводится i

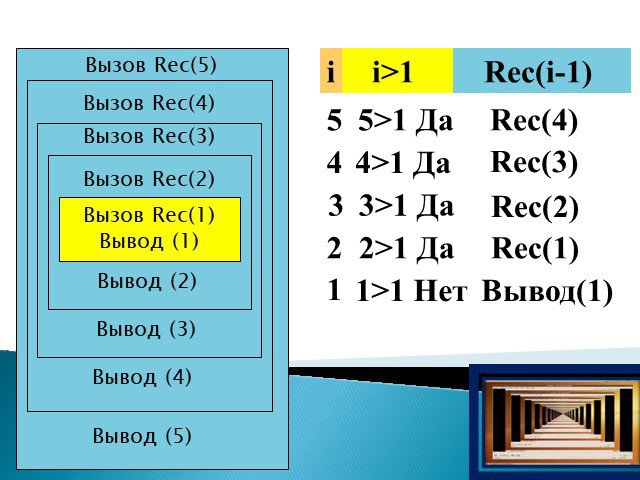
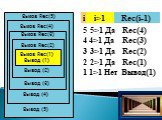
Вызов Rec(5) Вызов Rec(4) Вызов Rec(3) Вызов Rec(2) Вызов Rec(1) Вывод (1) Вывод (2) Вывод (3) Вывод (4) Вывод (5) i>1 i Rec(i-1) 5 4 3 2 1 5>1 Да 4>1 Да 3>1 Да 2>1 Да 1>1 Нет Rec(4) Rec(3) Rec(2) Rec(1) Вывод(1)

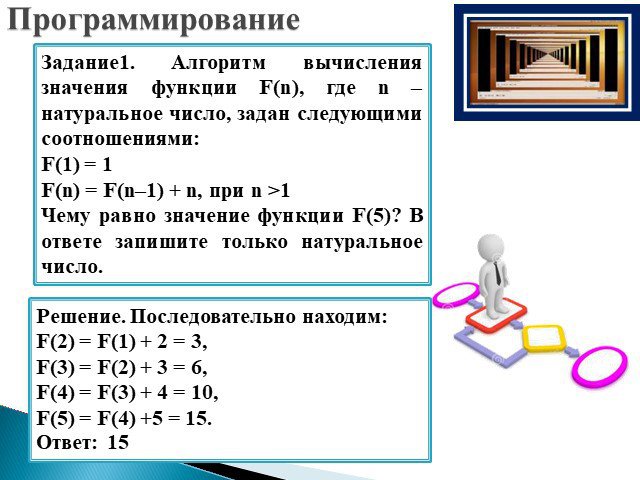
Задание1. Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями: F(1) = 1 F(n) = F(n–1) + n, при n >1 Чему равно значение функции F(5)? В ответе запишите только натуральное число.

Решение. Последовательно находим: F(2) = F(1) + 2 = 3, F(3) = F(2) + 3 = 6, F(4) = F(3) + 4 = 10, F(5) = F(4) +5 = 15. Ответ: 15

Задание 2. Дан рекурсивный алгоритм: procedure F(n: integer); begin writeln(n); if n

Складывая все эти числа, получаем 49

Задание 3. Дан рекурсивный алгоритм: procedure F(n: integer); begin writeln(n); if n

Складывая все эти числа, получаем 79

Задание 4. Дан рекурсивный алгоритм procedure F(n: integer); begin if n

Решение: Найдем значение процедуры: F(6)=F(5)+2*F(4) F(5)=F(4)+2*F(3) F(4)=F(3)+2*F(2) F(3)=F(2)+2*F(0)=F(2)+2*1=F(2)+2 F(2)=1 Следовательно: F(3)=1+2=3 F(4)=3+2*1=5 F(5)=5+2*3=11 F(6)=11+2*5=21

Задание 5. Дан рекурсивный алгоритм: procedure F(n: integer); begin writeln(n); if n F(2) F(4) F(3) F(8) F(5) F(6) 8+4+5+2+3+4+6+8+5=45

Построенное дерево позволяет ответить на более сложный вопрос: «Что напечатает программа?» Выписав значения узлов в порядке построения, получим: 2 4 8 5 3 6 4 8 5 Результат работы программы при ином расположении оператора печати n, в общем случае, отличается от данного.

Задание 5. Дан рекурсивный алгоритм: procedure F(n: integer); begin writeln(n); if n

Решение (II способ): При n4 F(8)=8; F(7)=7; F(6)=6; F(5)=5 Найдем значение процедуры: F(4)=4 +F(2*4)+F(4+1)=4+F(8)+F(5)= =4+8+5=17 F(3)=3 +F(2*3)+F(3+1)=3+F(6)+F(4)= =3+6+17=26 F(2)=2 +F(2*2)+F(2+1)=2+F(4)+F(3)= =2+17+26=45

Задание 6. Дан рекурсивный алгоритм procedure F(n: integer); begin if n

Решение: при n4 F(n)=n Найдем значение процедуры: F(2)=F(2*2)+F(2+1)+2=F(4)+F(3)+2 F(3)=F(2*3)+F(3+1)+3=F(6)+F(4)+3 F(4)=F(2*4)+F(4+1)+4=F(8)+F(5)+4 F(2)=F(8)+F(5)+4+F(6)+F(8)+F(5)+4+3+2

Ответ: 8,5,4,6,8,5,4,3,2

Задание 7. Дан рекурсивный алгоритм procedure F(n: integer); begin if n

Решение: при n4 F(n)= «не печатает!» Найдем значение процедуры: F(2)=F(2*2)+2+F(2+1)=F(4)+2+F(3) F(3)=F(2*3)+3+F(3+1)=F(6)+3+F(4) F(4)=F(2*4)+4+F(4+1)=F(8)+4+F(5) F(2)=4+2+F(3)=4+2+3+F(4)=4+2+3+4

Ответ: 4,2,3,4

Задание 8. Дан рекурсивный алгоритм procedure F(n: integer); begin if n >1 then begin F(n-2); write(n); F(n div 2); end; end; Укажите через запятую последовательность выводимых чисел, в том порядке, как их напечатает программа при выполнении вызова F(6).

Решение: при n>1 F(n)=F(n-2)+n +F(n div 2) при n Ответ: 2,4,2,6,3

Задание 9. Дан рекурсивный алгоритм procedure F(n: integer); Begin write(n); if n >1 then begin F(n-2); F(n div 2); end; end; Укажите через запятую последовательность выводимых чисел, в том порядке, как их напечатает программа при выполнении вызова F(5).

Решение: при n>1 F(n)=n+F(n-2) +F(n div 2) при n Ответ: 5,3,1,1,2,0,1

Задание 10. Даны два рекурсивных алгоритма procedure F(n: integer); forward; procedure G(n: integer); forward procedure F(n: integer); Begin write(‘*’); if n >0 then F(n-2) else G(n); end; procedure G(n: integer); Begin write(‘**’); if n >1 then F(n-3); end; Сколько символов «звездочка» будет напечатано на экране при выполнении F(20)?

Решение: при n>10 F(n)=‘*’+F(n-2) при n Ответ: 17

F(1)=3 F(4)=3+3=6 F(7)=3+6=9 F(10)=3+9=12 F(12)=1+12=13 F(14)=1+13=14 F(16)=1+14=15 F(18)=1+15=16 F(20)=1+16=17

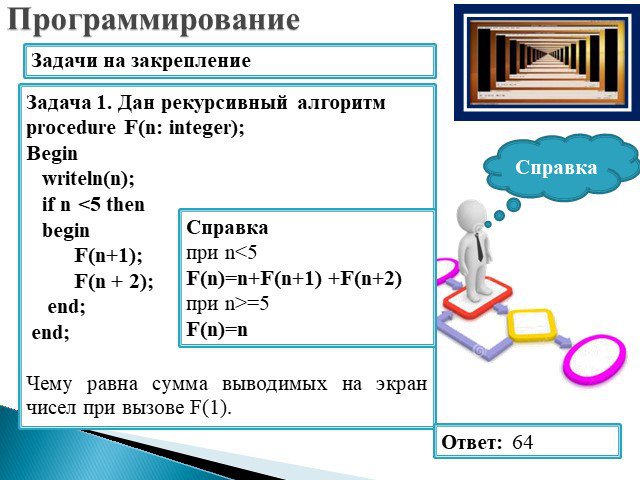
Задача 1. Дан рекурсивный алгоритм procedure F(n: integer); Begin writeln(n); if n Ответ: 64

Задачи на закрепление

Справка при n=5 F(n)=n

Справка

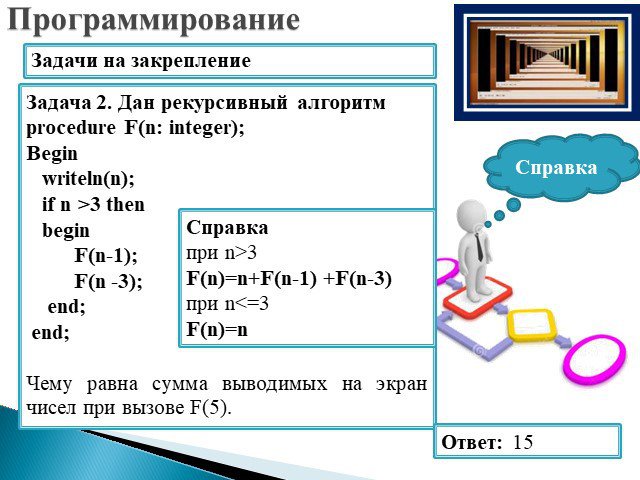
Задача 2. Дан рекурсивный алгоритм procedure F(n: integer); Begin writeln(n); if n >3 then begin F(n-1); F(n -3); end; end; Чему равна сумма выводимых на экран чисел при вызове F(5).

Ответ: 15

Справка при n>3 F(n)=n+F(n-1) +F(n-3) при n

Задача 3. Даны два рекурсивных алгоритма procedure F(n: integer); forward; procedure G(n: integer); forward procedure F(n: integer); Begin write(‘*’); if n >10 then F(n-2) else G(n); end; procedure G(n: integer); Begin write(‘**’); if n >0 then F(n-3); end; Сколько символов «звездочка» будет напечатано на экране при выполнении F(18)?

Ответ: 19

Задача 4. Даны два рекурсивных алгоритма procedure F(n: integer); forward; procedure G(n: integer); forward procedure F(n: integer); Begin write(‘*’); if n >=2 then F(n-2) else G(n); end; procedure G(n: integer); Begin write(‘**’); if n >1 then F(n-3); end; Сколько символов «звездочка» будет напечатано на экране при выполнении F(22)?

Ответ: 18

Задача 5. Даны два рекурсивных алгоритма procedure F(n: integer); forward; procedure G(n: integer); forward procedure F(n: integer); Begin write(n); if n mod 2 =0 then F(n div 2) else G((n-1) div 2); end; procedure G(n: integer); Begin write(n); if n >0 then F(n); end; Какова сумма чисел, напечатанных на экране при выполнении вызова F(17)?

Ответ: 40

Задача 6. Даны два рекурсивных алгоритма procedure F(n: integer); forward; procedure G(n: integer); forward procedure F(n: integer); Begin write(n mod 2); if n mod 2 =0 then F(n div 2) else G((n-1) div 2); end; procedure G(n: integer); Begin write(n); if n >0 then F(n); end; Какова сумма чисел, напечатанных на экране при выполнении вызова F(19)?

Ответ: 16

Задача 7. Даны два рекурсивных алгоритма procedure F(n: integer); forward; procedure G(n: integer); forward procedure F(n: integer); Begin write(n mod 2); if n mod 2 =0 then F(n div 2) else G((n-1) div 2); end; procedure G(n: integer); Begin write(n mod 2); if n >0 then F(n); end; Сколько нулей будет выведено на экране при выполнении вызова F(21)?

Ответ: 5

Задача 8. Даны два рекурсивных алгоритма procedure F(n: integer); forward; procedure G(n: integer); forward procedure F(n: integer); Begin if n mod 5 =0 then G(n -5) else F(n-3); end; procedure G(n: integer); Begin write(‘*’); if n >0 then F(n-1); end; Сколько символов «звездочка» будет напечатано на экране при выполнении вызова F(51)?

Ответ: 4

Список использованной литературы

Крылов С.С ЕГЭ 2017. Информатика Тематические тестовые задания/С.С. Крылов, Д.М. Ушаков.-М.:Издательство «Экзамен», 2017 Крылов С.С, Чуркина Т.Е. ЕГЭ. Информатика и ИКТ: типовые экзаменационные варианты: 20 вариантов. -М.:Издательство «Национальное образование», 2017 Бражникова О.В. Рекурсия. Рекурсивные алгоритмы http://easyen.ru Исламов Р.Г. «Рекурсивные алгоритмы». Разбор заданий №11 ЕГЭ по информатике и ИКТ Коротун О.В. Рекурсивные алгоритмы. Задание 11 ЕГЭ. http://proteacher.ru/2015/01/10/Rekursivnye_algoritmy_1420913156_12749.pptx Юдин А.Б. Рекрусия http://www.uchportal.ru/load/18-1-0-55354

Слайд 1, 2 http://arxweb.net/pictures/raznoe/recursia.jpeg Слайд 3-7,17,18,20-36, 44 https://upload.wikimedia.org/wikipedia/commons/b/b3/Screenshot_Recursion_via_vlc.png Слайд 3 http://lols.ru/uploads/posts/2011-07/1309983680_1309964j.jpg Слайд 7 Змей http://ezolan.ru/image/cache/data/Talisman/smola/kumirnica/95-500x500.jpg Зеркала http://cdn01.ru/files/users/images/92/44/92443e52bffa0b4f29b8075eb6a50193.jpg Матрешки https://image.jimcdn.com/app/cms/image/transf/none/path/seb6ba021dbaf218c/image/i0b5fd1e834074150/version/1418029668/image.jpg Слайд 8 Лем http://tomuz.ru/uploads/images/l/e/m/lem_stanislav_kiberiada_01_skazki_robotov.jpg Портрет https://fs00.infourok.ru/images/doc/233/91173/2/img4.jpg Мастер и Маргарита  http://biblus.ru/pics/7/f/f/1005817671.jpg Слайд 9 Гамлет http://botinok.co.il/sites/default/files/images/c44e9d5e0c2582fb3bfd9c60e1e36ea5_smoktunovskiy_gamlet.jpg Дон Кихот https://upload.wikimedia.org/wikipedia/commons/thumb/a/ac/Honoré_Daumier_017_%28Don_Quixote%29.jpg/416px-Honoré_Daumier_017_%28Don_Quixote%29.jpg Война и мир http://www.abbyreader.ru/pic/fa649070809c3dfb3fa768b4d8fd528a.jpg Слайд 10 Поп http://cdn01.ru/files/users/images/e4/31/e4311658d876f53c249807107fc54648.jpg Джек http://s-marshak.ru/books/d/d27/d27_02.jpg Слайд 11 https://lh3.googleusercontent.com/-SqgOCQ0nNsk/TKnKgCfpcKI/AAAAAAAAHe4/1E4isRsTzeEJBdFNBeDLDEp_RRH-VHnEgCHM/s800/0_2910a_67b4058a_XL.jpg

Интернет-ресурсы

Слайд 12 Руки https://1.bp.blogspot.com/-fbcn-arPJ-U/VzcSEzMsn0I/AAAAAAAALfQ/JOwbBZ2BLaMtAL1mNK-e7ZPt_OAPkAksgCLcB/s1600/drawing-hands.jpg Галерея http://escherdroste.math.leidenuniv.nl/images/scan450.jpg Слайд 13 Эйфелева башня http://ic.pics.livejournal.com/alexey_soloviev/41323646/48823/48823_original.jpg Музей http://akademichesky.mos.ru/upload/medialibrary/38e/git.jpg Фрактал http://lurkmore.so/images/a/a8/Fractal_pyramid.jpg Слайд 14 Подсолнух http://thefaceshop.info/image/data/подсолнечник.jpg Дерево http://slavaveto.ru/notes/images/the_tree.jpg Река http://static.panoramio.com/photos/large/53740152.jpg Шишки http://traffic-moscow.ru/img/elovie-shishki-v-retseptah-narodnoy-meditsini-3.jpg Слайд 15 http://monemo.ru/uploads/2963/images/ecaeb3a20d09ba73.jpg Слайд 16 http://picsview.ru/images/930461_flag-rossii-s-gerbom-png.jpg Слайд 17 http://yavix.ru/i/1/1/7/1f5e585142098e76790c71553053d.jpg Слайд 18 Факториал http://a887.phobos.apple.com/us/r30/Purple1/v4/7a/1a/7e/7a1a7e1e-85d1-dbb9-22dc-0491dbc71b71/pr_source.png?downloadKey=1428831233_243c912f63c872b85a411a2fb282a4f2 Фибоначи http://binarnyestrategii.ru/wp-content/uploads/2015/10/fibonacci-luchshaya-strategiaya.png Слайд 19 http://perego-shop.ru/gallery/images/1223129_zolotoe-sechenie-v-kosmose.jpg Слайд 21-36 Человечек http://sch2.luninec.edu.by/be/sm.aspx?guid=6463 Слайд 37-42 http://ivanov-shkola-70.myjino.ru/informatika_06_fgos/par_17/ris_62.png Слайд 43 http://s00.yaplakal.com/pics/pics_original/0/5/2/377250.jpg