Презентация "Алгебра логики Логические операции" по информатике – проект, доклад
Презентацию на тему "Алгебра логики Логические операции" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Информатика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 21 слайд(ов).
Слайды презентации
Список похожих презентаций
Алгебра логики Логическое умножение, сложение и отрицание
Алгебра высказываний. Алгебра высказываний была разработана для того, чтобы можно было определять истинность или ложность составных высказываний, ...Алгебра логики вторая часть
Мышление. Логика – наука о формах и способах мышления. Основные формы мышления – понятие, высказывание, умозаключение. Понятие – форма мышления, фиксирующая ...Алгебра логики
Еще живший в 384 - 322 г.г. до нашей эры древнегреческий ученый и философ Аристотель (Ἀριστοτέλης) пытался найти ответ на вопрос “Как мы рассуждаем”, ...Алгебра логики
Понятие- это форма человеческого мышления, где фиксируются основные, существенные признаки объекта. Любое понятие состоит из двух составляющих: объёма ...Алгебра логики первая часть
Логика - это наука о формах и способах мышления. Понятие; Высказывание; Умозаключение. Основные формы мышления:. это форма мышления, фиксирующая основные, ...Основы логики логические основы компьютера
Логика –это наука о формах и способах мышления;особая форма мышления. Понятие - это форма мышления, фиксирующая основные, существенные признаки объекта. ...Алгебра логики
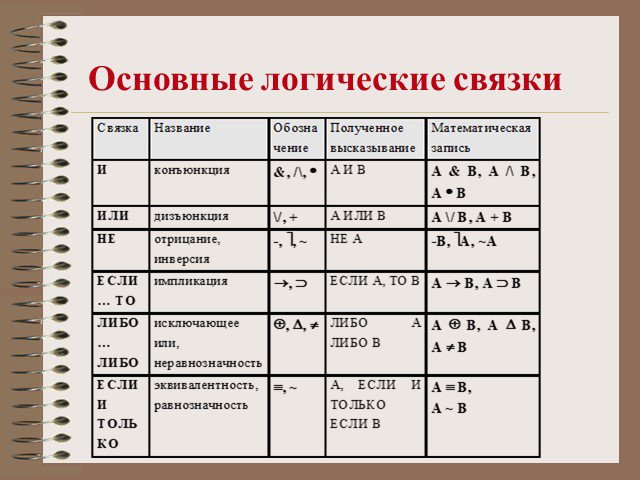
Содержание. Алгебра логики Логическое высказывание Простое и сложное высказывания Основные логические связки Основные логические операции Триггер ...Алгебра логики
Функции алгебры логики (булевы функции). . Основные законы алгебры логики. 1) Законы нулевого множества. 2) Законы универсального множества. 3) Законы ...Основы логики и логические основы компьютера
Выполните умозаключение. Логические элементы являются основой построения компьютеров. Элементной базой компьютеров являются вентили. Вентили – это ...Логические величины, операции, выражения
Основные понятия. Слово логика означает совокупность правил, которым подчиняется процесс мышления. Сам термин "логика" происходит от древнегреческого ...Логика и логические операции
История логики. Логика – наука о формах правильного мышления (рассуждения). Термин происходит от греческого слова «логос», что значит рассуждение. ...Логические величины, операции, выражения
Логические величины. Логические величины: понятия, выражаемые словами: ИСТИНА, ЛОЖЬ (true, false). Следовательно, истинность высказываний выражается ...Истинность высказываний. Логические операции
Прочитай высказывания. Выбери истинные.Зимой воробьи впадают в спячку. Великий русский ученый Ломоносов родился в 1711 году. Пройденное расстояние ...
Простые стандартные типы данных. Операции с числовыми переменными. Логические операции
Величины целого типа. Пример описания. const a=3; var a:integer; i:byte;. Величины вещественного типа. const max=3.45;c=2.1E2; Var summa:real;. Символьные ...Основы логики и логические основы построения компьютера
Процессор компьютера выполняет арифметические и логические операции над двоичными кодами. И поэтому чтобы иметь представление об устройстве компьютера, ...Логические операции. Таблицы истинности
Цели: Образовательная: Закрепить понятия: логическая переменная, логические операции, сформировать умения применения логических операций, умение составлять ...Логические операции
Логическая переменная. Логическая переменная - это простое высказывание, содержащее только одну мысль. Ее символическое обозначение — латинская буква ...Логические операции и таблицы истинности
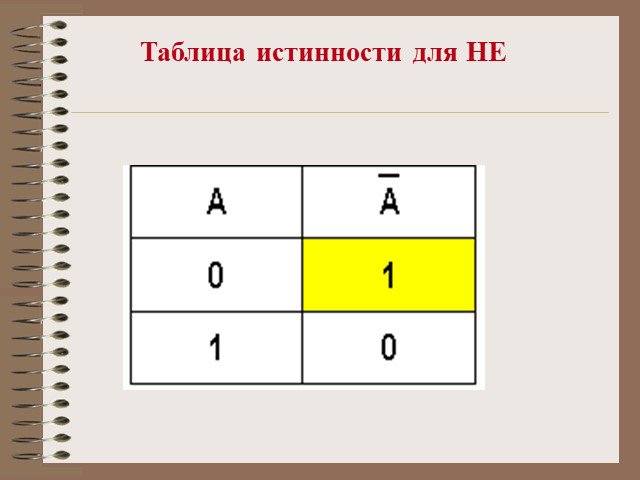
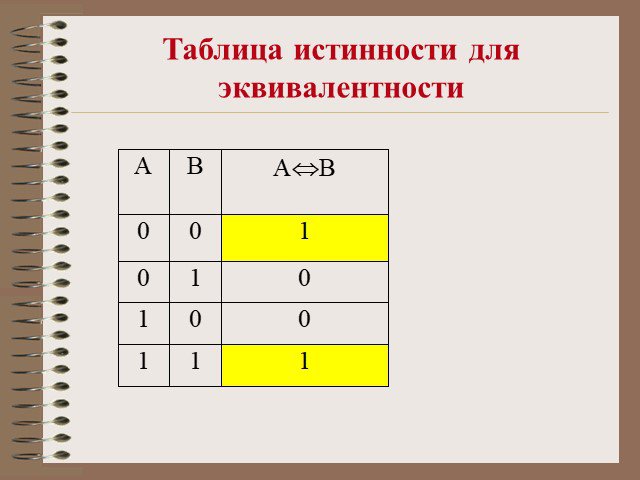
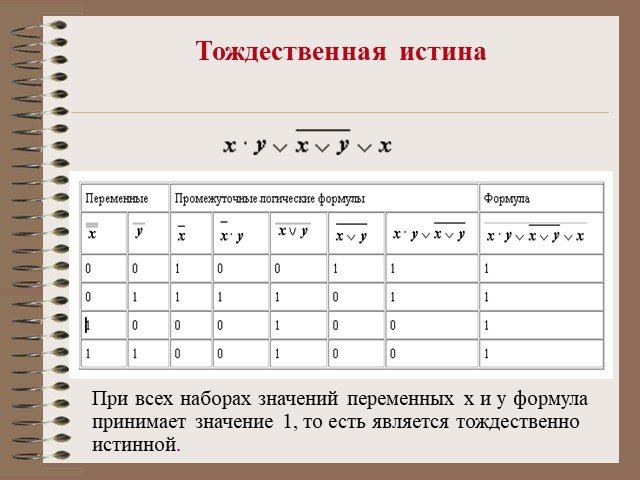
Таблица истинности — это таблица, устанавливающая соответствие между возможными наборами значений логических переменных и значениями функций. При ...Логические операции и таблицы истинности
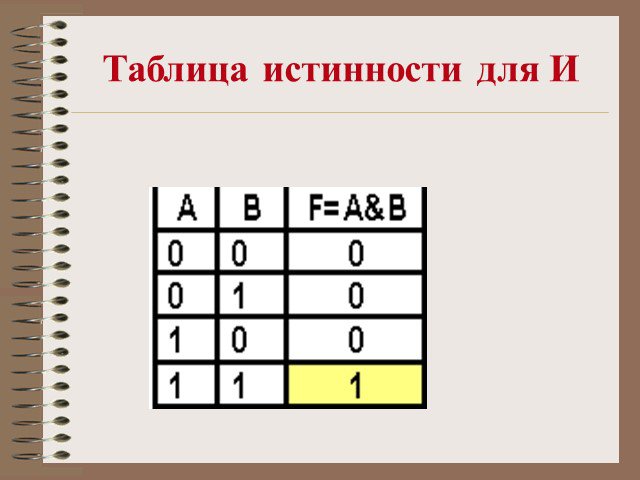
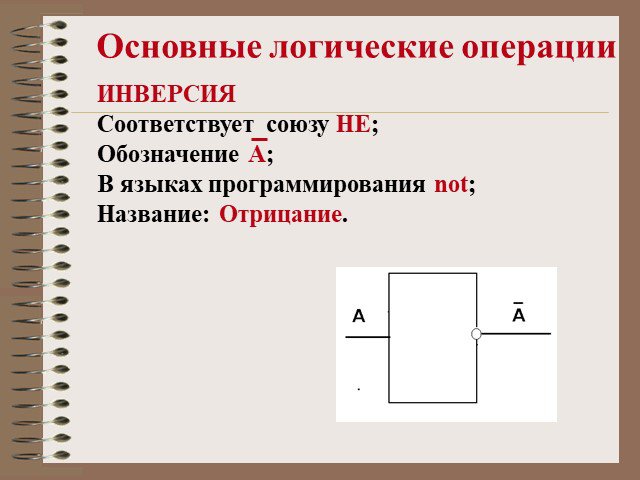
КОНЪЮНКЦИЯ. F = A & B. Логическое умножение КОНЪЮНКЦИЯ - это новое сложное выражение будет истинным только тогда, когда истинны оба исходных простых ...Логические операции
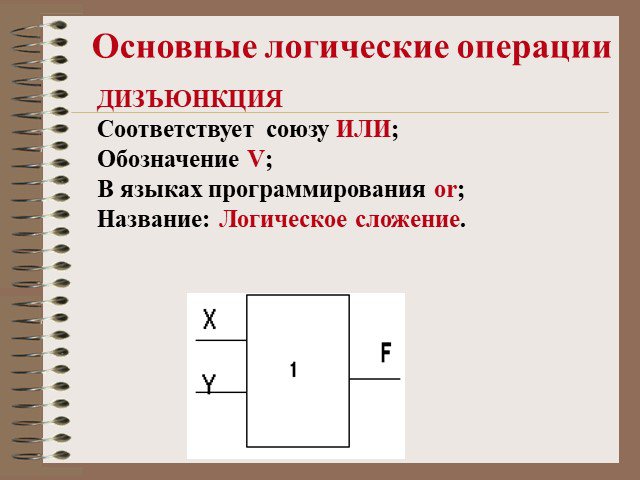
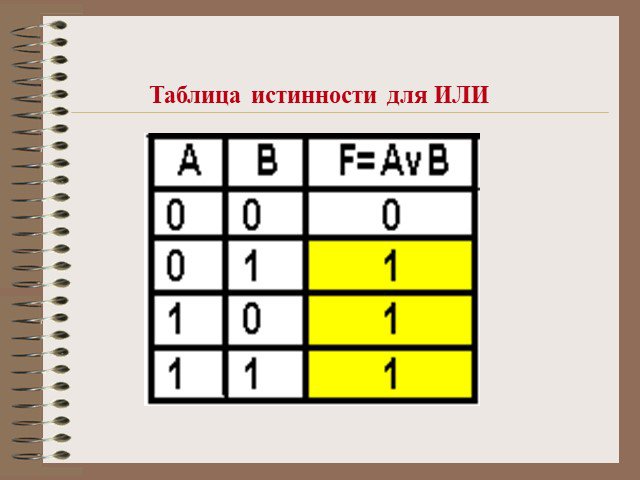
Конъюнкция. Таблица истинности. Диаграмма Эйлера-Венна. А В. Пересечение множеств. C=A&B. Дизъюнкция. Объединение множеств. C=A۷B. Инверсия Ā. Импликация. ...Конспекты
Логические операции
Муниципальное образовательное учреждение средняя общеобразовательная школа № 63 г. Ульяновск. Урок информатики в 9 классе. «Логические ...Высказывание. Логические операции
МОУ «Северная средняя общеобразовательная школа № 2. . Белгородского района Белгородской области». Конспект урока:. . . «Высказывание. ...Представление чисел в компьютере. Арифметические действия над целыми числами. Арифметические операции над числами с плавающей точкой
Тема. Представление чисел в компьютере. Арифметические действия над целыми числами. Арифметические операции над числами с плавающей точкой. Цель ...Построение таблиц истинности. Логические схемы
Конспект урока с применением ДОТ по информатике и ИКТ. . в 10 классе на тему «Построение таблиц истинности. Логические схемы». Автор:. Дугина ...Основы логики
Конспект урока с элементами ФГОС на тему «Основы логики». (9 класс). Цели:. . . Образовательная:. определяет понятия: понятие, высказывание, ...Основы логики
. Муниципальное общеобразовательное учреждение –. . средняя общеобразовательная школа №4 г. Асино Томской области. Конспект ...Логические элементы ПК. Построение функциональных схем
Автор Зорина Ольга Александровна. . Место работы МБОУ СОШ №7 г.Новый Уренгой. Должность учитель информатики. . Урок информатики в 9 классе. ...Логические основы построения компьютера
Учитель информатики Быргазова Юлия Александровна, МБОУ Гимназия № 9 г.Усолье-Сибирское электронный адрес:. shruar. _78@m. ail. .ru. Законы логики. ...Логические основы построения компьютера
ПЛАН-КОНСПЕКТ УРОКА:. «Логические операции». 1. ФИО. . . Соколова Людмила Ивановна. . 2. . Место работы. . ГБОУ СОШ №276, ...Логические выражения и таблицы истинности
Муниципальное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа №70 г. Липецка. Конспект урока по информатике ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Информатика
Автор презентации:Неизвестен
Содержит:21 слайд(ов)
Поделись с друзьями:
Скачать презентацию