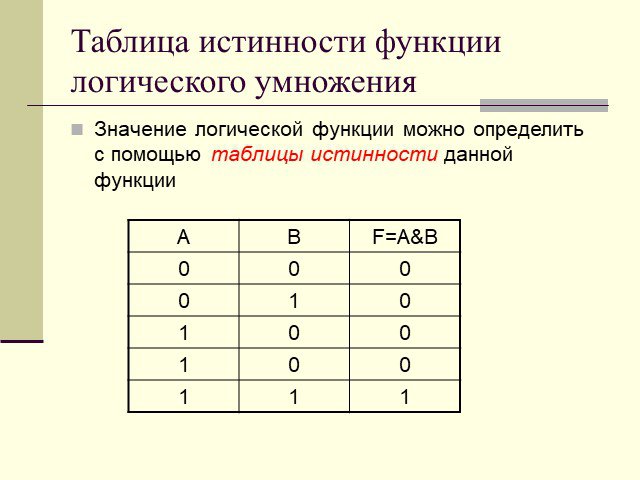
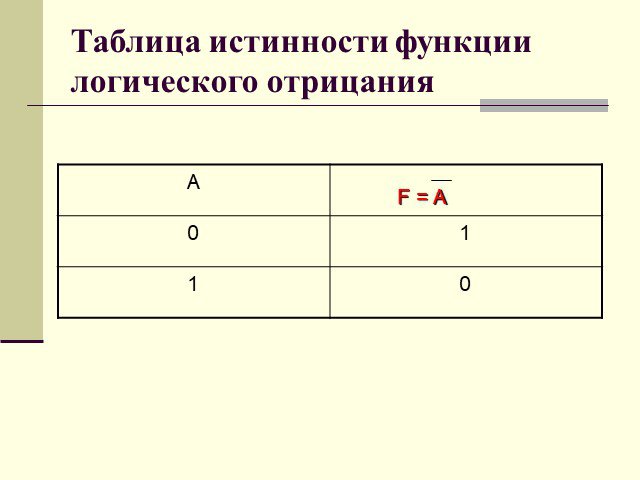
Презентация "Алгебра логики Логическое умножение, сложение и отрицание" по информатике – проект, доклад
Презентацию на тему "Алгебра логики Логическое умножение, сложение и отрицание" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Информатика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 14 слайд(ов).
Слайды презентации
Список похожих презентаций
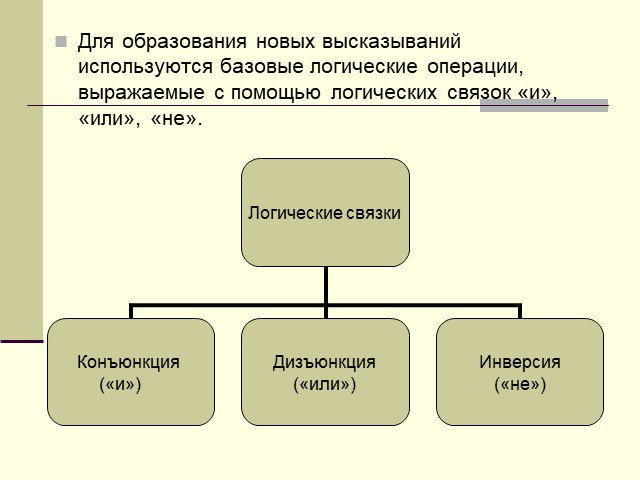
Алгебра логики Логические операции
Логика. Логика – это наука о формах и законах человеческой мысли, о законах доказательных рассуждений, изучающая методы доказательств и опровержений, ...Алгебра логики вторая часть
Мышление. Логика – наука о формах и способах мышления. Основные формы мышления – понятие, высказывание, умозаключение. Понятие – форма мышления, фиксирующая ...Алгебра логики
Еще живший в 384 - 322 г.г. до нашей эры древнегреческий ученый и философ Аристотель (Ἀριστοτέλης) пытался найти ответ на вопрос “Как мы рассуждаем”, ...Алгебра логики
Понятие- это форма человеческого мышления, где фиксируются основные, существенные признаки объекта. Любое понятие состоит из двух составляющих: объёма ...Алгебра логики первая часть
Логика - это наука о формах и способах мышления. Понятие; Высказывание; Умозаключение. Основные формы мышления:. это форма мышления, фиксирующая основные, ...Логическое сложение
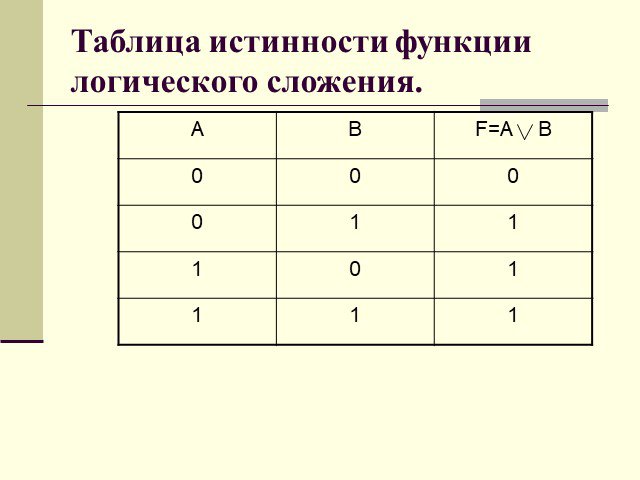
ОПРЕДЕЛЕНИЕ:. Объединение двух (или нескольких высказываний) с помощью союза «или» называется операцией логического сложения или дизъюнкцией. Обозначение ...Алгебра логики
Содержание. Алгебра логики Логическое высказывание Простое и сложное высказывания Основные логические связки Основные логические операции Триггер ...Алгебра логики
Функции алгебры логики (булевы функции). . Основные законы алгебры логики. 1) Законы нулевого множества. 2) Законы универсального множества. 3) Законы ...Основы логики и логические основы компьютера
Выполните умозаключение. Логические элементы являются основой построения компьютеров. Элементной базой компьютеров являются вентили. Вентили – это ...Основы логики - построение таблиц истинности
При изучении работы различных устройств компьютера приходится рассматривать такие его логические элементы, в которых реализуются сложные логические ...Основы логики
Презентация к уроку информатики в 4 классе по программе А.В.Горячева (IV четверть 8 урок). Повторение. Алгоритмы и исполнители. Какие действия могут ...Основы логики
ФОРМЫ МЫШЛЕНИЯ. Логика – это наука о формах и способах мышления. Это учение о способах рассуждения и доказательств. Мышление. Понятие – выделение ...Основы логики
ЛОГИКА -- ЭТО УЧЕНИЕ О СПОСОБАХ РАССУЖДЕНИЙ И ДОКАЗАТЕЛЬСТВ, НАУКА О ЗАКОНАХ И ФОРМАХ МЫШЛЕНИЯ. «LOGOS» -- СЛОВО, МЫСЛЬ, ПОНЯТИЕ, РАССУЖДЕНИЕ, ЗАКОН. ...Основы логики
Логика – это наука о формах и способах мышления. Основы формальной логики заложил Аристотель, который впервые отделил логические формы мышления (речи) ...Основы логики
ЛОГИКА - НАУКА О ЗАКОНАХ И ФОРМАХ ПРАВИЛЬНОГО МЫШЛЕНИЯ. ЭВМ необходима при решении логических задач. Наверное, многие из вас перевозили волка, козла ...Основы логики
Логика – это наука о формах и способах мышления. ОСНОВНЫЕ ПОНЯТИЯ: Д. Буль (1815-1864). Основные формы мышления. Понятие Умозаключение Высказывание. ...Основы математической логики
Слово логика означает совокупность правил, которым подчиняется процесс мышления. Сам термин "логика" происходит от древнегреческого logos, означающего ...Основы логики и логические основы построения компьютера
Процессор компьютера выполняет арифметические и логические операции над двоичными кодами. И поэтому чтобы иметь представление об устройстве компьютера, ...Логическое программирование
Содержание. Определение и алгоритм решения головоломок Поиск в пространстве решений (в глубину/ширину) Примеры решения логических задач Общие выводы. ...Законы алгебры логики
Логическая формула-это выражение, содержащее логические константы, логические переменные, знаки логических операций. Логическая функция – зависимость ...Конспекты
Основы логики
. Муниципальное общеобразовательное учреждение –. . средняя общеобразовательная школа №4 г. Асино Томской области. Конспект ...Основы логики
Конспект урока с элементами ФГОС на тему «Основы логики». (9 класс). Цели:. . . Образовательная:. определяет понятия: понятие, высказывание, ...Использование элементов алгебры логики при решении заданий ЕГЭ по информатике
Муниципальное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа № 2 п. Мостовского. муниципального образования Мостовский ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Информатика
Автор презентации:Диденко В.В.
Содержит:14 слайд(ов)
Поделись с друзьями:
Скачать презентацию