Слайд 1Логическое программирование
Презентация 10 Решение логических задач
Слайд 2Содержание
Определение и алгоритм решения головоломок Поиск в пространстве решений (в глубину/ширину) Примеры решения логических задач Общие выводы

Слайд 3Логические задачи (головоломки)
Логическая головоломка состоит из нескольких фактов относительно небольшого числа объектов, которые имеют различные атрибуты. Минимальное число фактов относительно объектов и атрибутов связано с желанием выдать единственный вариант назначения атрибутов объектам. Зачастую в задаче устанавливается взаимно-однозначное соответствие между двумя множествами. Если этих ограничений нет, то задача сильно усложняется (при неоднозначности могут появиться альтернативные решения, потребоваться вмешательство пользователя в решение и т.п.). Общий алгоритм решения головоломок: Перечисляются действующие лица, их допустимые атрибуты Задаются известные факты об атрибутах лиц и их взаимосвязях Задается вопрос, соответствующий исходному заданию, происходит вызов предиката поиска решений Решение выдается в виде конкретизированных переменных (если таковые были заданы), либо выводится на экран командами типа write

Слайд 4Пример головоломки
Условие: Беседуют трое друзей: Белов, Рыжов, Чернов. Брюнет сказал Белову: «Посмотри, один из нас блондин, другой – рыжий, третий – брюнет, но ни у кого цвет волос не соответствует его фамилии». Вопрос: какой цвет волос у каждого собеседника?
Слайд 5Решение головоломки
surname('Белов'). surname('Чернов'). surname('Рыжов'). color('рыжий'). color('светлый'). color('черный'). hair(X, Y) :- surname(X), color(Y), X='Белов', not(Y='черный'), not(Y='светлый'). hair(X, Y) :- surname(X), color(Y), X='Чернов', not(Y='черный'), not(hair('Белов', Y)). hair(X, Y) :- surname(X), color(Y), X='Рыжов', not(hair('Белов', Y)), not(hair('Чернов', Y)).
Слайд 6Поиск решения головоломки
% Конкретизируем переменные X и Y допустимыми значениями % эти значения и будут искомыми решениями задачи ?- hair(X, Y). X = 'Белов' Y = рыжий ; X = 'Чернов' Y = светлый ; X = 'Рыжов' Y = черный ; No
Слайд 7Более сложный пример: поиск соответствий
В автомобильных гонках три первых места заняли Алеша, Петя и Коля. Какое место занял каждый из них, если Петя занял не второе и не третье место, а Коля - не третье? Сперва запишем факты (очевидные данные): /* База данных имен */ имя(алеша). имя(петя). имя(коля). /* База данных призовых мест */ место(первое). место(второе). место(третье).

Слайд 8Запишем правила и предикат поиска решения /* Устанавливаем взаимно-однозначное соответствие между базами данных, X - элемент из базы данных имен, Y - элемент из базы данных занятых мест */ /* Петя занял не второе и не третье место */ соответствие(X, Y) :- имя(X), X=петя, место(Y), not(Y=второе), not(Y=третье). /* Коля занял не третье место */ соответствие(X, Y) :- имя(X), X=коля, место(Y), not(Y=третье). соответствие(X, Y) :- имя(X), X=алеша, место(Y). /* У всех ребят разные места */ решение(X1,Y1,X2,Y2,X3,Y3) :- X1=петя, соответствие(X1,Y1), X2=коля, соответствие(X2,Y2), X3=алеша, соответствие(X3,Y3), Y1\=Y2, Y2\=Y3, Y1\=Y3.
Слайд 9Запускаем решатель…
?- решение(X1,Y1,X2,Y2,X3,Y3). X1 = петя Y1 = первое X2 = коля Y2 = второе X3 = алеша Y3 = третье
Слайд 10Логические задачи
Пространство состояний - это граф, вершины которого соответствуют ситуациям, встречающимся в задаче ("проблемные ситуации"), а решение задачи сводится к поиску пути в этом графе. Примеры задач, где используется поиск в пространстве состояний: Ханойские башни Задача о волке, козе и капусте Игра в 15 Задача коммивояжера Другие логические задачи (эвристика, олимпиадные задачи, проблемы ИИ,…) Рассмотрим на примерах, как формулируются задачи в терминах пространства состояний, а также обсудим общие методы решения сооотв. задач. Процесс решения задачи включает в себя поиск в графе, при этом, как правило, возникает проблема, как обрабатывать альтернативные пути поиска. Мы рассмотрим две основные стратегии перебора альтернатив: поиск в глубину и поиск в ширину.

Слайд 11Пример: задача с кубиками
Задача состоит в выработке плана переупорядочивания кубиков, поставленных друг на друга, как показано на рисунке. На каждом шагу разрешается переставлять только один кубик. Кубик можно взять только тогда, когда его верхняя поверхность свободна. Кубик можно поставить либо на стол, либо на другой кубик. Для того, чтобы построить требуемый план, мы должны отыскать последовательность ходов, реализующую заданную трансформацию. Эту задачу можно представлять себе как задачу выбора среди множества возможных альтернатив. В исходной ситуации альтернатива всего одна: поставить кубик С на стол. После того как кубик С поставлен на стол, мы имеем три альтернативы: поставить А на стол или поставить А на С, или поставить С на А.

Слайд 12Граф состояний
Как показывает рассмотренный пример, с задачами такого рода связано два типа понятий: Проблемные ситуации. Разрешенные ходы или действия, преобразующие одни проблемные ситуации в другие. Проблемные ситуации вместе с возможными ходами образуют направленный граф, называемый пространством состояний. Вершины графа соответствуют проблемным ситуациям, дуги - разрешенным переходам из одних состояний в другие. Задача отыскания плана решения задачи эквивалентна задаче построения пути между заданной начальной ситуацией ("стартовой" вершиной) и некоторой указанной заранее конечной ситуацией, называемой также целевой вершиной.
Примечание: Каждому разрешенному ходу или действию можно приписать его стоимость. Например, в нашей задаче стоимости, приписанные перемещениям кубиков, будут указывать нам на то, что некоторые кубики перемещать труднее, чем другие. В тех случаях, когда каждый ход имеет стоимость, мы заинтересованы в отыскании решения минимальной стоимости. Стоимость решения - это сумма стоимостей дуг, из которых состоит "решающий путь" - путь из стартовой вершины в целевую. Либо может потребоваться найти кратчайший путь по кол-ву состояний…
![Решение задачи о кубиках. % удаление элемента Х из списка, результат - в L del(X, [X | L], L). del(X, [Y | L], [Y | L1]):- del(X, L, L1). % переход между состояниями: s(X, Y) % где X - предыдущий, Y - последующий допустимый шаг/состояние % перенести верхний кубик Top1 на столбик Stack2 s( Stacks, [S Решение задачи о кубиках. % удаление элемента Х из списка, результат - в L del(X, [X | L], L). del(X, [Y | L], [Y | L1]):- del(X, L, L1). % переход между состояниями: s(X, Y) % где X - предыдущий, Y - последующий допустимый шаг/состояние % перенести верхний кубик Top1 на столбик Stack2 s( Stacks, [S](https://prezentacii.org/upload/cloud/18/11/93468/images/thumbs/screen13.jpg)
Слайд 13Решение задачи о кубиках
% удаление элемента Х из списка, результат - в L del(X, [X | L], L). del(X, [Y | L], [Y | L1]):- del(X, L, L1). % переход между состояниями: s(X, Y) % где X - предыдущий, Y - последующий допустимый шаг/состояние % перенести верхний кубик Top1 на столбик Stack2 s( Stacks, [Stackl, [Top1 | Stack2] | OtherStacks] ) :- del([Top1 | Stackl], Stacks, Stacksl), % Найти первый столбик del(Stack2, Stacksl, OtherStacks). % Найти второй столбик goal(Situation):- member([a,b,c], Situation). % Целевое состояние Алгоритмы поиска реализуются в программе в виде отношения: solve(Start, Solution) где Start — начальный узел в пространстве состояний, a Solution — путь от узла Start до любого целевого узла. % Вызов поиска: ?- solve([[c,a,b], [], []], Solution). % Определение см. далее
![Стратегия поиска в глубину. Для того, чтобы найти решающий путь Sol из заданной вершины N в некоторую целевую вершину, необходимо: если N - это целевая вершина, то положить Sol = [N], или если для исходной вершины N существует вершина-преемник N1, такая, что можно провести путь Sol1 из N1 в целевую Стратегия поиска в глубину. Для того, чтобы найти решающий путь Sol из заданной вершины N в некоторую целевую вершину, необходимо: если N - это целевая вершина, то положить Sol = [N], или если для исходной вершины N существует вершина-преемник N1, такая, что можно провести путь Sol1 из N1 в целевую](https://prezentacii.org/upload/cloud/18/11/93468/images/thumbs/screen14.jpg)
Слайд 14Стратегия поиска в глубину
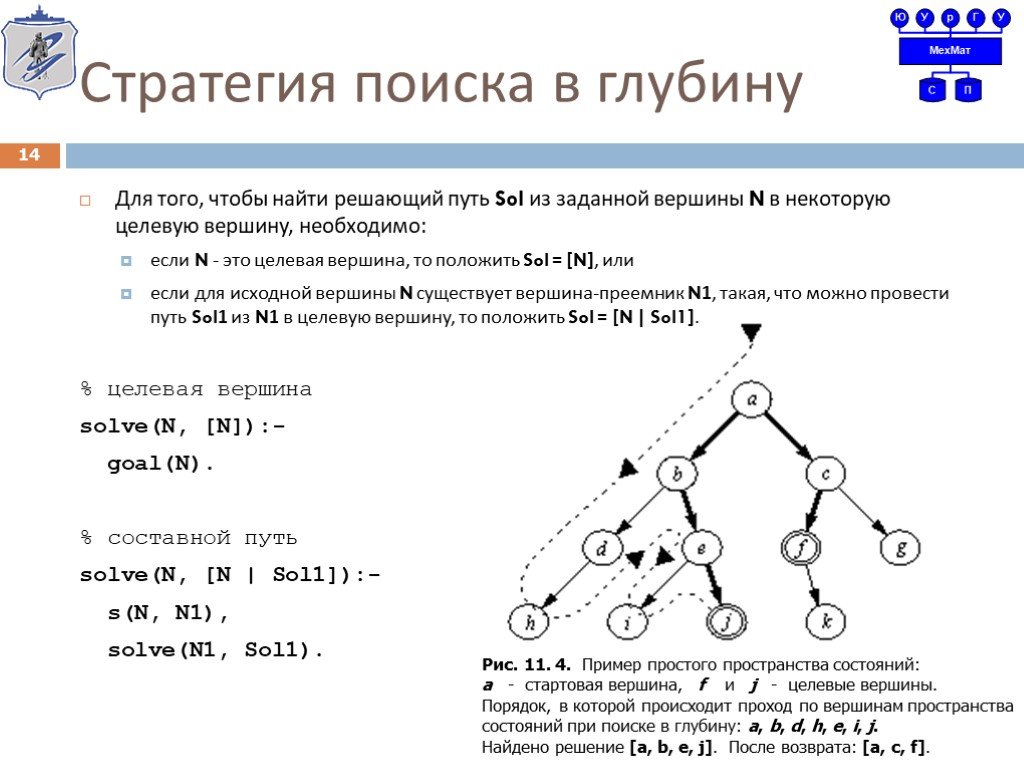
Для того, чтобы найти решающий путь Sol из заданной вершины N в некоторую целевую вершину, необходимо: если N - это целевая вершина, то положить Sol = [N], или если для исходной вершины N существует вершина-преемник N1, такая, что можно провести путь Sol1 из N1 в целевую вершину, то положить Sol = [N | Sol1]. % целевая вершина solve(N, [N]):- goal(N). % составной путь solve(N, [N | Sol1]):- s(N, N1), solve(N1, Sol1).
Рис. 11. 4. Пример простого пространства состояний: а - стартовая вершина, f и j - целевые вершины. Порядок, в которой происходит проход по вершинам пространства состояний при поиске в глубину: а, b, d, h, e, i, j. Найдено решение [a, b, e, j]. После возврата: [а, с, f].

Слайд 15Оптимизация поиска: избавляемся от циклов
Мы говорим "в глубину", имея в виду тот порядок, в котором рассматриваются альтернативы в пространстве состояний. Всегда, когда алгоритму поиска в глубину надлежит выбрать из нескольких вершин ту, в которую следует перейти для продолжения поиска, он предпочитает самую "глубокую" из них. Самая глубокая вершина - это вершина, расположенная дальше других от стартовой вершины Поиск в глубину наиболее адекватен рекурсивному стилю программирования, принятому в Прологе. Причина этого состоит в том, что, обрабатывая цели, пролог-система сама просматривает альтернативы именно в глубину. Очевидное усовершенствование – добавление механизма обнаружения циклов: Ни одну из вершин, уже содержащихся в пути, построенном из стартовой вершины в текущую вершину, не следует вторично рассматривать в качестве возможной альтернативы продолжения поиска. Правило можно сформулировать в виде: depthfirst( Path, Node, Solution)
Начинаясь в а, поиск заканчивается бесконечным циклом между d и h: a, b, d, h, d, h, d ...
![Реализация поиска в глубину без зацикливаний. % solve( Node, Solution): % Решение Solution представляет собой ациклический путь (узлы в % котором указаны в обратном порядке) между узлом Node и целью solve( Node, Solution):- depthfirst( [], Node, Solution). % depthfirst( Path, Node, Solution): % реше Реализация поиска в глубину без зацикливаний. % solve( Node, Solution): % Решение Solution представляет собой ациклический путь (узлы в % котором указаны в обратном порядке) между узлом Node и целью solve( Node, Solution):- depthfirst( [], Node, Solution). % depthfirst( Path, Node, Solution): % реше](https://prezentacii.org/upload/cloud/18/11/93468/images/thumbs/screen16.jpg)
Слайд 16Реализация поиска в глубину без зацикливаний
% solve( Node, Solution): % Решение Solution представляет собой ациклический путь (узлы в % котором указаны в обратном порядке) между узлом Node и целью solve( Node, Solution):- depthfirst( [], Node, Solution). % depthfirst( Path, Node, Solution): % решение Solution формируется в результате продления пути % [Node | Path] до целевого узла depthfirst( Path, Node, [Node | Path] ) :- goal( Node). depthfirst( Path, Node, Sol) :- s( Node, Node1), not member( Node1, Path), % Предотвращение цикла depthfirst( [Node | Path], Node1, Sol).

Слайд 17Поиск в ширину
В противоположность поиску в глубину стратегия поиска в ширину предусматривает переход в первую очередь к вершинам, ближайший к стартовой вершине. В результате процесс поиска имеет тенденцию развиваться более в ширину, чем в глубину (см. рис). Поиск в ширину программируется не так легко, как поиск в глубину. Причина состоят в том, что нам приходится сохранять все множество альтернативных вершин-кандидатов, а не только одну вершину, как при поиске в глубину. Более того, если мы желаем получить при помощи процесса поиска решающий путь, то одного множества вершин недостаточно. Поэтому мы будем хранить не множество вершин-кандидатов, а множество путей-кандидатов. Таким образом, цель breadthfirst( Paths, Solution) истинна только тогда, когда существует путь из множества кандидатов Пути, который может быть продолжен вплоть до целевой вершины. Этот продолженный путь и есть Solution.
![Граф поиска в ширину. Простое пространство состояний: а - стартовая вершина, f и j - целевые вершины. Применение стратегии поиска в ширину дает следующий порядок прохода по вершинам: а, b, c, d, e, f. Более короткое решение: [a, c, f] найдено раньше, чем более длинное: [а, b, e, j] Граф поиска в ширину. Простое пространство состояний: а - стартовая вершина, f и j - целевые вершины. Применение стратегии поиска в ширину дает следующий порядок прохода по вершинам: а, b, c, d, e, f. Более короткое решение: [a, c, f] найдено раньше, чем более длинное: [а, b, e, j]](https://prezentacii.org/upload/cloud/18/11/93468/images/thumbs/screen18.jpg)
Слайд 18Граф поиска в ширину
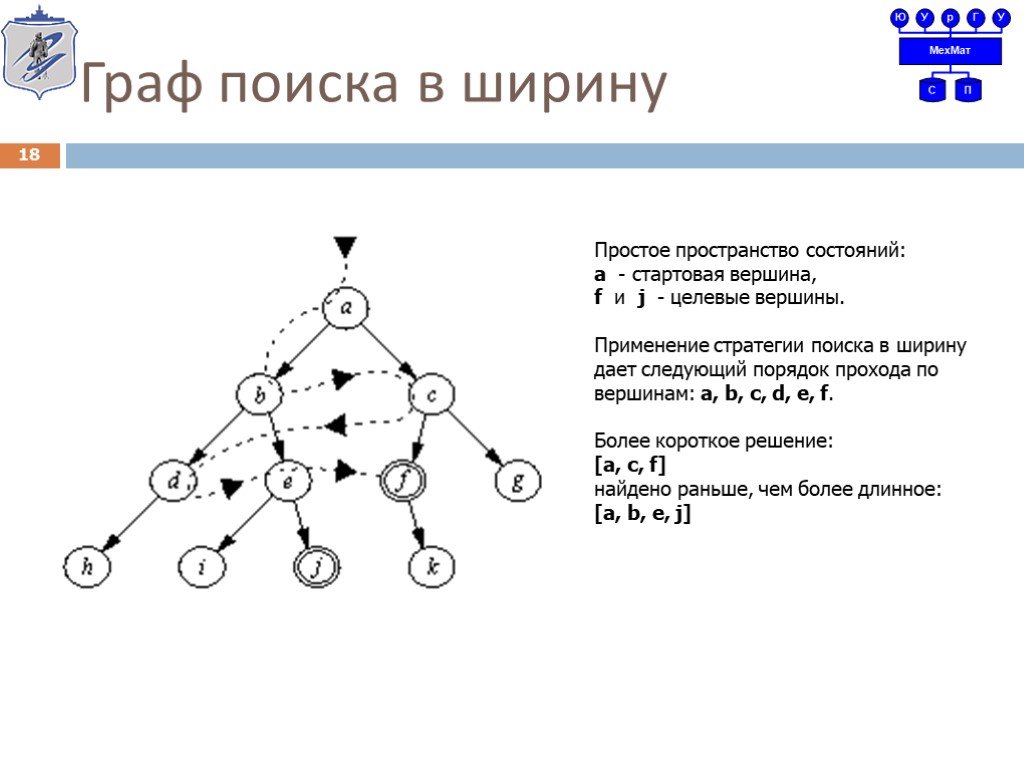
Простое пространство состояний: а - стартовая вершина, f и j - целевые вершины. Применение стратегии поиска в ширину дает следующий порядок прохода по вершинам: а, b, c, d, e, f. Более короткое решение: [a, c, f] найдено раньше, чем более длинное: [а, b, e, j]

Слайд 19Реализация поиска в ширину
Чтобы выполнить поиск в ширину при заданном множестве путей нужно: если голова первого пути - это целевая вершина, то взять этот путь в качестве решения иначе удалить первый путь из множества кандидатов и породить множество всех возможных продолжений этого пути на один шаг; множество продолжений добавить в конец множества кандидатов, а затем выполнить поиск в ширину с полученным новым множеством. % solve( Start, Solution): % Решение Solution – путь из вершины Start к цели solve( Start, Solution) :- breadthfirst( [ [Start] | Z] - Z, Solution). breadthfirst( [ [Node | Path] | _] - _, [Node | Path] ) :- goal( Node). breadthfirst( [Path | Paths] - Z, Solution) :- extend( Path, NewPaths), conc( NewPaths, Z1, Z), % Добавить NewPaths в конец Paths \== Z1, % Множество возможных путей – не пустое breadthfirst( Paths - Z1, Solution).

Слайд 20Задача о ханойской башне
Автор: математик Люка,1883 год. "Где-то в непроходимых джунглях, недалеко от города Ханоя, есть монастырь бога Брамы. В начале времен, когда Брама создавал Мир, он воздвиг в этом монастыре три высоких алмазных стержня и на один из них возложил 64 диска, сделанных из чистого золота. Он приказал монахам перенести эту башню на другой стержень (в соответствии с правилами, разумеется). С этого времени монахи работают день и ночь. Когда они закончат свой труд, наступит конец света." В нашем примере будем использовать всего 4 диска и 3 стержня. Правила перемещения дисков: разрешается снимать со стержня только верхний диск, запрещается класть больший диск на меньший, при каждом ходе передвигается только один диск. В решении будем использовать рекурсивный поиск всевозможных вариантов.

Слайд 21Решение задачи о Ханойских башнях
% move(число_дисков, откуда, куда, через) move(1,X,Y,_) :- write('Перемещаем диск с '), write(X), write(' стержня на '), write(Y), nl. move(N,X,Y,Z) :- N>1, M is N-1, move(M,X,Z,Y), move(1,X,Y,_), move(M,Z,Y,X). % Предикат для запуска поиска решений задачи размерности X hanoi(X):- move(X, 'лев.', 'прав.', 'центр.').

Слайд 22Находим решение ханойской задачи…
?- hanoi(4). Перемещаем диск с лев. стержня на центр. Перемещаем диск с лев. стержня на прав. Перемещаем диск с центр. стержня на прав. Перемещаем диск с лев. стержня на центр. Перемещаем диск с прав. стержня на лев. Перемещаем диск с прав. стержня на центр. Перемещаем диск с лев. стержня на центр. Перемещаем диск с лев. стержня на прав. Перемещаем диск с центр. стержня на прав. Перемещаем диск с центр. стержня на лев. Перемещаем диск с прав. стержня на лев. Перемещаем диск с центр. стержня на прав. Перемещаем диск с лев. стержня на центр. Перемещаем диск с лев. стержня на прав. Перемещаем диск с центр. стержня на прав. Yes

Слайд 23Более сложная задача: Фермер (вол-коза-капуста)
Условия: Действующие лица: фермер ( Farmer ), волк ( Wolf ), козел ( Goat ) капуста ( Cabbidge ) находятся на одном (правом) берегу У берега находится лодка, в которую могут поместиться только двое. Нельзя оставлять на одном берегу козу и капусту, козу и волка. Задание: Надо перебраться на другой (левый) берег на лодке.
Слайд 24Решение задачи: описание условий
% противоположные берега opposite('ПРАВ.', 'ЛЕВ.'). opposite('ЛЕВ.', 'ПРАВ.'). % возможные перемещения move(state(X,X,G,C), state(Y,Y,G,C)):- opposite(X,Y). /* фермер с волком */ move(state(X,W,X,C), state(Y,W,Y,C)):- opposite(X,Y). /* фермер с козой */ move(state(X,W,G,X), state(Y,W,G,Y)):- opposite(X,Y). /* фермер с капустой */ move(state(X,W,G,C), state(Y,W,G,C)):- opposite(X,Y). /* фермер один */ % недопустимые состояния unsafe( state(F,X,X,_) ):- opposite(F,X). % волк съест козу unsafe( state(F,_,X,X) ):- opposite(F,X). % коза съест капусту
Слайд 25Поиск путей решения
path(S,G,L,L1):- move(S,S1), not( unsafe(S1) ), not( member(S1,L) ), path( S1,G,[S1|L],L1),!. path(G,G,T,T):- !. % найдено финальное состояние % Для вызова решения можно использовать: go:- go(state('ПРАВ.','ПРАВ.','ПРАВ.','ПРАВ.'), state('ЛЕВ.','ЛЕВ.','ЛЕВ.','ЛЕВ.')). go(S,G):- path(S,G,[S],L), nl,write('Порядок перемещений (решение):'), nl, write_path(L), fail. go(_,_).
![Для организации удобной формы вывода…. member(X,[X|_]). member(X,[_|L]):- member(X,L). write_move( state(X,W,G,C), state(Y,W,G,C) ) :-!, write('Фермер переплывает реку с '), write(X), write(' реки на '), write(Y), nl. write_move( state(X,X,G,C), state(Y,Y,G,C) ) :-!, write('Фермер перевозит волка с Для организации удобной формы вывода…. member(X,[X|_]). member(X,[_|L]):- member(X,L). write_move( state(X,W,G,C), state(Y,W,G,C) ) :-!, write('Фермер переплывает реку с '), write(X), write(' реки на '), write(Y), nl. write_move( state(X,X,G,C), state(Y,Y,G,C) ) :-!, write('Фермер перевозит волка с](https://prezentacii.org/upload/cloud/18/11/93468/images/thumbs/screen26.jpg)
Слайд 26Для организации удобной формы вывода…
member(X,[X|_]). member(X,[_|L]):- member(X,L). write_move( state(X,W,G,C), state(Y,W,G,C) ) :-!, write('Фермер переплывает реку с '), write(X), write(' реки на '), write(Y), nl. write_move( state(X,X,G,C), state(Y,Y,G,C) ) :-!, write('Фермер перевозит волка с '), write(X), write(' берега реки на '), write(Y), nl. write_move( state(X,W,X,C), state(Y,W,Y,C) ) :-!, write('Фермер перевозит козу с ' ), write(X), write(' берега реки на '), write(Y), nl. write_move( state(X,W,G,X), state(Y,W,G,Y) ) :-!, write('Фермер перевозит капусту с '), write(X), write(' берега реки на '), write(Y), nl. write_path( [H1,H2|T] ) :- !, write_move(H1,H2),write_path([H2|T]). write_path( _ ).

Слайд 27Получаем готовое решение
?- go. Порядок перемещений (решение): Фермер перевозит козу с ЛЕВ. берега реки на ПРАВ. Фермер переплывает реку с ПРАВ. реки на ЛЕВ. Фермер перевозит капусту с ЛЕВ. берега реки на ПРАВ. Фермер перевозит козу с ПРАВ. берега реки на ЛЕВ. Фермер перевозит волка с ЛЕВ. берега реки на ПРАВ. Фермер переплывает реку с ПРАВ. реки на ЛЕВ. Фермер перевозит козу с ЛЕВ. берега реки на ПРАВ. Yes

Слайд 28Еще одна головоломка…
Побег от Зурга Персонажи фильма «История игрушек»: Базз, Вуди, Рекс и Хэмм - убегают от Зурга. Им осталось только перейти через последний мост, и они будут свободны. Однако, мост очень ветхий и сможет одновременно выдержать только двоих из них. Также, что бы перейти мост и не попасть в ловушки и ямы в нём, нужен фонарик. Проблема в том, что у наших четырёх друзей всего один фонарик и заряда батареи в нём осталось всего лишь на 60 (шестьдесят) минут. Игрушки могут перейти мост в одну сторону за различное время: Игрушка Время Базз 5 минут Вуди 10 минут Рекс 20 минут Хэмм 25 минут Так как одновременно на мосту могут находиться только две игрушки, они не могут перейти мост сразу все вместе. Так как им нужен фонарик для перехода через мост, кому-то из двоих, перешедших через мост, нужно будет вернуться к оставшимся игрушкам, что бы отдать им фонарик. Вопрос: в каком порядке эти четыре игрушки должны пересечь мост за время не более 60 минут, что бы спастись от Зурга?
![Решение задачи «Побег от Зурга». % факты: время прохождения моста каждым героем time(buzz, 5). time(woody,10). time(rex, 20). time(hamm, 25). % список действующих персонажей toys([buzz,hamm,rex,woody]). cost([],0) :- !.% цена перехода моста равно 0, если все перешли cost([X|L],C) :- % иначе равна вр Решение задачи «Побег от Зурга». % факты: время прохождения моста каждым героем time(buzz, 5). time(woody,10). time(rex, 20). time(hamm, 25). % список действующих персонажей toys([buzz,hamm,rex,woody]). cost([],0) :- !.% цена перехода моста равно 0, если все перешли cost([X|L],C) :- % иначе равна вр](https://prezentacii.org/upload/cloud/18/11/93468/images/thumbs/screen29.jpg)
Слайд 29Решение задачи «Побег от Зурга»
% факты: время прохождения моста каждым героем time(buzz, 5). time(woody,10). time(rex, 20). time(hamm, 25). % список действующих персонажей toys([buzz,hamm,rex,woody]). cost([],0) :- !.% цена перехода моста равно 0, если все перешли cost([X|L],C) :- % иначе равна времени самого медлительного time(X,S), cost(L,D), C is max(S,D). % вспомогательный предикат: вычисляется каждая допустимая группа % игрушек, двигающаяся направо (выдает списки длины 2) split(L,[X,Y],M) :- member(X,L), % если X есть в L member(Y,L), % и Y есть в L compare(

Слайд 30Продолжение решения: определяем допустимые переходы
/* Идея – в представлении промежуточных состояний переходов через мост фактами вида st(P,L), где L - список игрушек, находящихся в данный момент на левой стороне моста, а P - признак, показывающий положение фонарика (левая или правая сторона) */ move(st(l,L1),st(r,L2),r(M),D) :- split(L1,M,L2), cost(M,D). move(st(r,L1),st(l,L2),l(X),D) :- toys(T), subtract(T,L1,R), member(X,R), merge_set([X],L1,L2), time(X,D). % trans/4 в основном генерирует все возможные переходы через мост вместе с требуемым временем trans(st(r,[]),st(r,[]),[],0). trans(S,U,L,D) :- move(S,T,M,X), trans(T,U,N,Y), append([M],N,L), D is X + Y.
Слайд 31Поиск решений
% cross/2 формулирует поисковую задачу, % задавая начальную и конечную конфигурации пространства поиска. cross(M,D) :- toys(T), trans(st(l,T),st(r,[]),M,D0), D0=

Слайд 32Задача о ферзях
Задача о расстановке на шахматной доске ферзей таким образом, чтобы ни один из ферзей не находился под боем другого. Для того, чтобы задача была решена, требуется расставить ферзей таким образом, чтобы все ферзи занимали разные горизонтали, разные вертикали и разные диагонали. Результат можно представить в виде списка, где каждый элемент списка - это координаты одного из ферзей. Заранее можно ограничить перебор, расставив ферзей по разным горизонталям. Решить поставленную задачу можно следующим образом: 1. если список ферзей пуст, то это одно из решений задачи; 2. если список ферзей не пуст, то он будет являться решением в случае, если ферзи в хвосте списка не будут бить друг друга, то есть хвост списка сам будет решением, и ферзь, находящийся в голове списка, не будет бить ни одного ферзя из хвоста списка.
![Решение задачи о ферзях. solution ([ ]). solution ([queen (X,Y)|Rest]):- solution (Rest), belongs (Y, [1,2,3,4,5,6,7,8]), notbeat (queen (X,Y),Rest). notbeat (_,[ ]):- !. notbeat (queen (X,Y), [queen (X1,Y1)|Rest]):- YY1, TmpY1=Y1-Y, TmpX1=X1-X, TmpY1TmpX1, TmpX=X-X1, TmpY1TmpX, notbeat (queen (X,Y) Решение задачи о ферзях. solution ([ ]). solution ([queen (X,Y)|Rest]):- solution (Rest), belongs (Y, [1,2,3,4,5,6,7,8]), notbeat (queen (X,Y),Rest). notbeat (_,[ ]):- !. notbeat (queen (X,Y), [queen (X1,Y1)|Rest]):- YY1, TmpY1=Y1-Y, TmpX1=X1-X, TmpY1TmpX1, TmpX=X-X1, TmpY1TmpX, notbeat (queen (X,Y)](https://prezentacii.org/upload/cloud/18/11/93468/images/thumbs/screen33.jpg)
Слайд 33Решение задачи о ферзях
solution ([ ]). solution ([queen (X,Y)|Rest]):- solution (Rest), belongs (Y, [1,2,3,4,5,6,7,8]), notbeat (queen (X,Y),Rest). notbeat (_,[ ]):- !. notbeat (queen (X,Y), [queen (X1,Y1)|Rest]):- YY1, TmpY1=Y1-Y, TmpX1=X1-X, TmpY1TmpX1, TmpX=X-X1, TmpY1TmpX, notbeat (queen (X,Y),Rest). belongs (X, [X|L]). belongs (X, [Y|L]):- belongs (X,L). templ ([queen (1,Y1),queen (2,Y2),queen (3,Y3),queen (4,Y4),queen (5,Y5),queen (6,Y6),queen (7,Y7),queen (8,Y8)]). start:- templ (S), write(S), solution(S), write(S), nl, fail.
![Полученные решения. [queen (1,4), queen (2,2), queen (3,7), queen (4,3), queen (5,6), queen (6,8), queen (7,5), queen (8,1)] [queen (1,5), queen (2,2), queen (3,4), queen (4,7), queen (5,3), queen (6,8), queen (7,6), queen (8,1)] [queen (1,3), queen (2,5), queen (3,2), queen (4,8), queen (5,6), quee Полученные решения. [queen (1,4), queen (2,2), queen (3,7), queen (4,3), queen (5,6), queen (6,8), queen (7,5), queen (8,1)] [queen (1,5), queen (2,2), queen (3,4), queen (4,7), queen (5,3), queen (6,8), queen (7,6), queen (8,1)] [queen (1,3), queen (2,5), queen (3,2), queen (4,8), queen (5,6), quee](https://prezentacii.org/upload/cloud/18/11/93468/images/thumbs/screen34.jpg)
Слайд 34Полученные решения
[queen (1,4), queen (2,2), queen (3,7), queen (4,3), queen (5,6), queen (6,8), queen (7,5), queen (8,1)] [queen (1,5), queen (2,2), queen (3,4), queen (4,7), queen (5,3), queen (6,8), queen (7,6), queen (8,1)] [queen (1,3), queen (2,5), queen (3,2), queen (4,8), queen (5,6), queen (6,4), queen (7,7), queen (8,1)] [queen (1,3), queen (2,6), queen (3,4), queen (4,2), queen (5,8), queen (6,5), queen (7,7), queen (8,1)] [queen (1,5), queen (2,7), queen (3,1), queen (4,3), queen (5,8), queen (6,6), queen (7,4), queen (8,2)] [queen (1,4), queen (2,6), queen (3,8), queen (4,3), queen (5,1), queen (6,7), queen (7,5), queen (8,2)] [queen (1,3), queen (2,6), queen (3,8), queen (4,1), queen (5,4), queen (6,7), queen (7,5), queen (8,2)] [queen (1,5), queen (2,3), queen (3,8), queen (4,4), queen (5,7), queen (6,1), queen (7,6), queen (8,2)] [queen (1,5), queen (2,7), queen (3,4), queen (4,1), queen (5,3), queen (6,8), queen (7,6), queen (8,2)] …

Слайд 35Выводы
Пространство состояний - это направленный граф, вершины которого соответствуют проблемным ситуациям, а дуги - возможным ходам. Конкретная задача определяется стартовой вершиной и целевым условием. Решению задачи соответствует путь в графе. Таким образом, решение задачи сводится к поиску пути в графе. Оптимизационные задачи моделируются приписыванием каждой дуге пространства состояний некоторой стоимости. Имеются две основных стратегии поиска в пространстве состояний - поиск в глубину и поиск в ширину. Поиск в глубину программируется наиболее легко, однако подвержен зацикливаниям. Существуют два простых метода предотвращения зацикливания: ограничить глубину поиска и не допускать дублирования вершин. Реализация поиска в ширину более сложна, поскольку требуется сохранять множество кандидатов. Это множество может быть с легкостью представлено списком списков, но более экономное представление - в виде дерева. Поиск в ширину всегда первым обнаруживает самое короткое решение, что не верно в отношении стратегии поиска в глубину.














































![Решение задачи о кубиках. % удаление элемента Х из списка, результат - в L del(X, [X | L], L). del(X, [Y | L], [Y | L1]):- del(X, L, L1). % переход между состояниями: s(X, Y) % где X - предыдущий, Y - последующий допустимый шаг/состояние % перенести верхний кубик Top1 на столбик Stack2 s( Stacks, [S Решение задачи о кубиках. % удаление элемента Х из списка, результат - в L del(X, [X | L], L). del(X, [Y | L], [Y | L1]):- del(X, L, L1). % переход между состояниями: s(X, Y) % где X - предыдущий, Y - последующий допустимый шаг/состояние % перенести верхний кубик Top1 на столбик Stack2 s( Stacks, [S](https://prezentacii.org/upload/cloud/18/11/93468/images/thumbs/screen13.jpg)
![Стратегия поиска в глубину. Для того, чтобы найти решающий путь Sol из заданной вершины N в некоторую целевую вершину, необходимо: если N - это целевая вершина, то положить Sol = [N], или если для исходной вершины N существует вершина-преемник N1, такая, что можно провести путь Sol1 из N1 в целевую Стратегия поиска в глубину. Для того, чтобы найти решающий путь Sol из заданной вершины N в некоторую целевую вершину, необходимо: если N - это целевая вершина, то положить Sol = [N], или если для исходной вершины N существует вершина-преемник N1, такая, что можно провести путь Sol1 из N1 в целевую](https://prezentacii.org/upload/cloud/18/11/93468/images/thumbs/screen14.jpg)

![Реализация поиска в глубину без зацикливаний. % solve( Node, Solution): % Решение Solution представляет собой ациклический путь (узлы в % котором указаны в обратном порядке) между узлом Node и целью solve( Node, Solution):- depthfirst( [], Node, Solution). % depthfirst( Path, Node, Solution): % реше Реализация поиска в глубину без зацикливаний. % solve( Node, Solution): % Решение Solution представляет собой ациклический путь (узлы в % котором указаны в обратном порядке) между узлом Node и целью solve( Node, Solution):- depthfirst( [], Node, Solution). % depthfirst( Path, Node, Solution): % реше](https://prezentacii.org/upload/cloud/18/11/93468/images/thumbs/screen16.jpg)

![Граф поиска в ширину. Простое пространство состояний: а - стартовая вершина, f и j - целевые вершины. Применение стратегии поиска в ширину дает следующий порядок прохода по вершинам: а, b, c, d, e, f. Более короткое решение: [a, c, f] найдено раньше, чем более длинное: [а, b, e, j] Граф поиска в ширину. Простое пространство состояний: а - стартовая вершина, f и j - целевые вершины. Применение стратегии поиска в ширину дает следующий порядок прохода по вершинам: а, b, c, d, e, f. Более короткое решение: [a, c, f] найдено раньше, чем более длинное: [а, b, e, j]](https://prezentacii.org/upload/cloud/18/11/93468/images/thumbs/screen18.jpg)






![Поиск путей решения. path(S,G,L,L1):- move(S,S1), not( unsafe(S1) ), not( member(S1,L) ), path( S1,G,[S1|L],L1),!. path(G,G,T,T):- !. % найдено финальное состояние % Для вызова решения можно использовать: go:- go(state('ПРАВ.','ПРАВ.','ПРАВ.','ПРАВ.'), state('ЛЕВ.','ЛЕВ.','ЛЕВ.','ЛЕВ.')). go(S,G):- Поиск путей решения. path(S,G,L,L1):- move(S,S1), not( unsafe(S1) ), not( member(S1,L) ), path( S1,G,[S1|L],L1),!. path(G,G,T,T):- !. % найдено финальное состояние % Для вызова решения можно использовать: go:- go(state('ПРАВ.','ПРАВ.','ПРАВ.','ПРАВ.'), state('ЛЕВ.','ЛЕВ.','ЛЕВ.','ЛЕВ.')). go(S,G):-](https://prezentacii.org/upload/cloud/18/11/93468/images/thumbs/screen25.jpg)
![Для организации удобной формы вывода…. member(X,[X|_]). member(X,[_|L]):- member(X,L). write_move( state(X,W,G,C), state(Y,W,G,C) ) :-!, write('Фермер переплывает реку с '), write(X), write(' реки на '), write(Y), nl. write_move( state(X,X,G,C), state(Y,Y,G,C) ) :-!, write('Фермер перевозит волка с Для организации удобной формы вывода…. member(X,[X|_]). member(X,[_|L]):- member(X,L). write_move( state(X,W,G,C), state(Y,W,G,C) ) :-!, write('Фермер переплывает реку с '), write(X), write(' реки на '), write(Y), nl. write_move( state(X,X,G,C), state(Y,Y,G,C) ) :-!, write('Фермер перевозит волка с](https://prezentacii.org/upload/cloud/18/11/93468/images/thumbs/screen26.jpg)


![Решение задачи «Побег от Зурга». % факты: время прохождения моста каждым героем time(buzz, 5). time(woody,10). time(rex, 20). time(hamm, 25). % список действующих персонажей toys([buzz,hamm,rex,woody]). cost([],0) :- !.% цена перехода моста равно 0, если все перешли cost([X|L],C) :- % иначе равна вр Решение задачи «Побег от Зурга». % факты: время прохождения моста каждым героем time(buzz, 5). time(woody,10). time(rex, 20). time(hamm, 25). % список действующих персонажей toys([buzz,hamm,rex,woody]). cost([],0) :- !.% цена перехода моста равно 0, если все перешли cost([X|L],C) :- % иначе равна вр](https://prezentacii.org/upload/cloud/18/11/93468/images/thumbs/screen29.jpg)

![Поиск решений. % cross/2 формулирует поисковую задачу, % задавая начальную и конечную конфигурации пространства поиска. cross(M,D) :- toys(T), trans(st(l,T),st(r,[]),M,D0), D0= Поиск решений. % cross/2 формулирует поисковую задачу, % задавая начальную и конечную конфигурации пространства поиска. cross(M,D) :- toys(T), trans(st(l,T),st(r,[]),M,D0), D0=](https://prezentacii.org/upload/cloud/18/11/93468/images/thumbs/screen31.jpg)

![Решение задачи о ферзях. solution ([ ]). solution ([queen (X,Y)|Rest]):- solution (Rest), belongs (Y, [1,2,3,4,5,6,7,8]), notbeat (queen (X,Y),Rest). notbeat (_,[ ]):- !. notbeat (queen (X,Y), [queen (X1,Y1)|Rest]):- YY1, TmpY1=Y1-Y, TmpX1=X1-X, TmpY1TmpX1, TmpX=X-X1, TmpY1TmpX, notbeat (queen (X,Y) Решение задачи о ферзях. solution ([ ]). solution ([queen (X,Y)|Rest]):- solution (Rest), belongs (Y, [1,2,3,4,5,6,7,8]), notbeat (queen (X,Y),Rest). notbeat (_,[ ]):- !. notbeat (queen (X,Y), [queen (X1,Y1)|Rest]):- YY1, TmpY1=Y1-Y, TmpX1=X1-X, TmpY1TmpX1, TmpX=X-X1, TmpY1TmpX, notbeat (queen (X,Y)](https://prezentacii.org/upload/cloud/18/11/93468/images/thumbs/screen33.jpg)
![Полученные решения. [queen (1,4), queen (2,2), queen (3,7), queen (4,3), queen (5,6), queen (6,8), queen (7,5), queen (8,1)] [queen (1,5), queen (2,2), queen (3,4), queen (4,7), queen (5,3), queen (6,8), queen (7,6), queen (8,1)] [queen (1,3), queen (2,5), queen (3,2), queen (4,8), queen (5,6), quee Полученные решения. [queen (1,4), queen (2,2), queen (3,7), queen (4,3), queen (5,6), queen (6,8), queen (7,5), queen (8,1)] [queen (1,5), queen (2,2), queen (3,4), queen (4,7), queen (5,3), queen (6,8), queen (7,6), queen (8,1)] [queen (1,3), queen (2,5), queen (3,2), queen (4,8), queen (5,6), quee](https://prezentacii.org/upload/cloud/18/11/93468/images/thumbs/screen34.jpg)































