Презентация "Системы представления знаний" по информатике – проект, доклад

Системы представления знаний

Лекция 6 Курс «Интеллектуальные информационные системы»

Системы представления знаний (СПЗ)

для ИС используют следующие основные виды моделей: Декларативные модели представления знаний (фреймовые модели, семантические сети) Процедурные модели представления знаний (исчисления предикатов, системы продукций)

Семантические сети

- это граф, дуги которого есть отношения между вершинами (значениями). Вершины (узлы) делятся на события, атрибуты, комплексы признаков и процедуры. Семантическую сеть можно рассматривать как композицию троек вида ArB, где A и B – два понятия, r – связь между ними

События:

Суждения, факты, результаты наблюдений, рекомендации. Могут представляться словосочетаниями и числами. Группируются тематически или функционально в разделы. События делятся на характеризуемые и характеризующие (события- признаки) Дождливая погода. Идет дождь

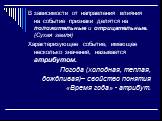
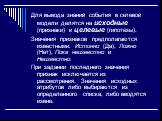
В зависимости от направления влияния на событие признаки делятся на положительные и отрицательные. (Сухая земля) Характеризующее событие, имеющее несколько значений, называется атрибутом. Погода (холодная, теплая, дождливая)– свойство понятия «Время года» - атрибут.

Процедуры

- специфические компоненты сети, выполняющие преобразования информации. Позволяют вычислять значения одних атрибутов на основании других, оперируя как с числами, так и с символами

Для вывода знаний события в сетевой модели делятся на исходные (признаки) и целевые (гипотезы). Значения признаков предполагаются известными: Истинно (Да), Ложно (Нет), Пока неизвестно и Неизвестно. При задании последнего значения признак исключается из рассмотрения. Значения исходных атрибутов либо выбираются из определенного списка, либо вводятся извне.

Объектами вывода в рассматриваемой модели являются гипотезы. К ним относятся рекомендации, диагнозы, прогнозы и другие решения, определяемые спецификой предметной области. Условием вывода должно быть существование хотя бы одной гипотезы. В данном случае решением является оценка ее истинности

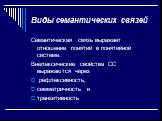
Виды семантических связей

Семантическая связь выражает отношение понятий в понятийной системе. Внелексические свойства СС выражаются через рефлексивность, симметричность и транзитивность

Rf – рефлексивность; Nrf – нерефлексивность; Arf – антирефлексивность (ни одной рефлексии); Sm – симметричность; Ns – несимметричность; Ans – антисимметричность (ни одной симметрии); As – асимметричность (контекстное свойство – обращение связи дает иную связь из списка); Tr – транзитивность; Ntr - нетранзитивность

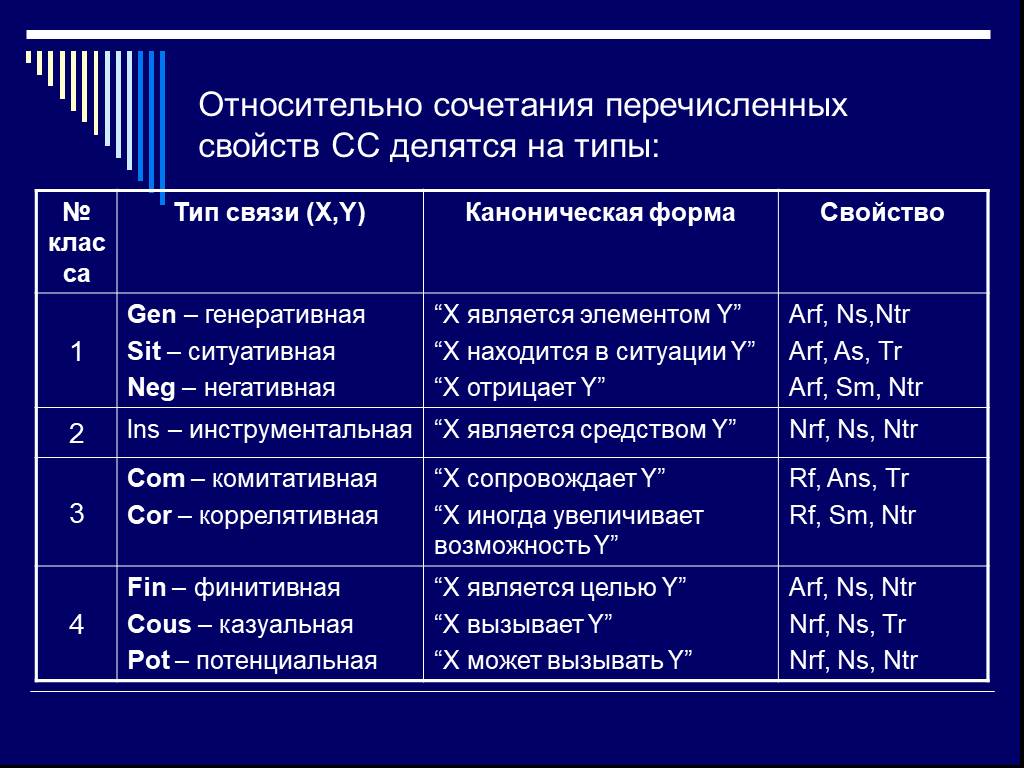
Относительно сочетания перечисленных свойств СС делятся на типы:

1. Рефлексивность определяется по критерию подстановки (ArB→BrB), выбирается один из ответов: Вполне возможно (тавтология) → Rf Не исключено → Nrf Невозможно → Arf Пример. Вегетативные расстройства сопровождаются вегетативными расстройствами. Ответ 1 для Com

2. Симметричность определяется по критерию перестановки (ArB→BrA) и выясняется справедливость полученного предложения. При утвердительном ответе высказыванию присваивается свойство Sm, в противном случае – свойство Ns. Пример. Головная боль всегда сопровождается вегетативными расстройствами, и вегетативные расстройства всегда сопровождаются головной болью. Ответ «Нет» для Com (свойство Ns)

3. Свойство Ns уточняется на более сильные свойства: Ans и As. Первое имеет место для любых примеров анализируемой связи. Например, для связи Com имеет место свойство Ans. 4. Для выявления свойства As используется критерий обращения: если высказывания A предикатор В и В предикатор А принадлежат различным типам высказываний в таблице, то имеет место свойство As.

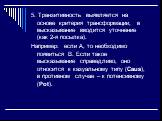
5. Транзитивность выявляется на основе критерия трансформации, в высказывание вводится уточнение (как 2-я посылка). Например: если А, то необходимо появиться В. Если такое высказывание справедливо, оно относится к казуальному типу (Caus), в противном случае – к потенсивному (Pot).

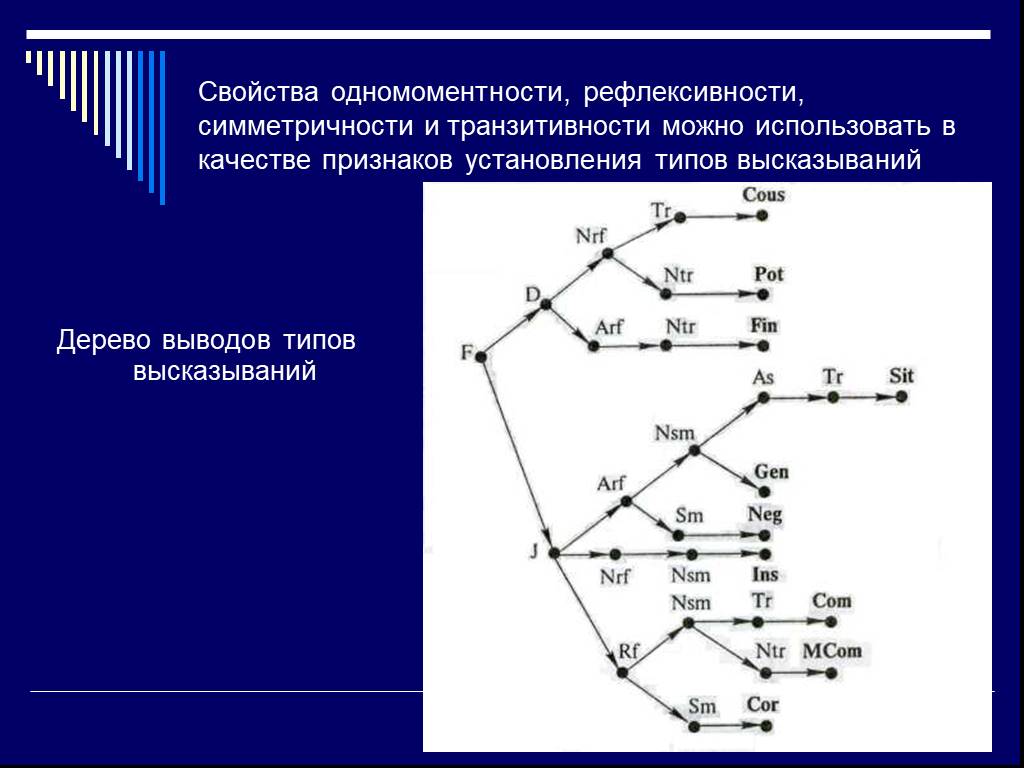
Группы 1-3 в таблице отражают одномоментные зависимости, группа 4 – разномоментную зависимость между объектами высказывания (следствие реализуется позже посылки). Типы связей групп 1-3 различаются свойством рефлексии. Внутри этих групп типы связей различаются по свойствам симметрии. Т.к. в группе 4 все связи обладают несимметричностью, то для их различения используют свойства рефлексивности и транзитивности.

Свойства одномоментности, рефлексивности, симметричности и транзитивности можно использовать в качестве признаков установления типов высказываний

Дерево выводов типов высказываний

Между двумя событиями реализованы следующие связи:

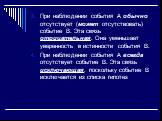
При наблюдении события А может наблюдаться (обычно наблюдается) событие В. Эта связь положительная. Она порождает событие В в качестве гипотезы или увеличивает уверенность в его истинности. При наблюдении события А всегда наблюдается событие В. Эта положительная связь более сильная.

При наблюдении события А обычно отсутствует (может отсутствовать) событие В. Эта связь отрицательная. Она уменьшает уверенность в истинности события В. При наблюдении события А всегда отсутствует событие В. Эта связь исключающая, поскольку событие В исключается из списка гипотез

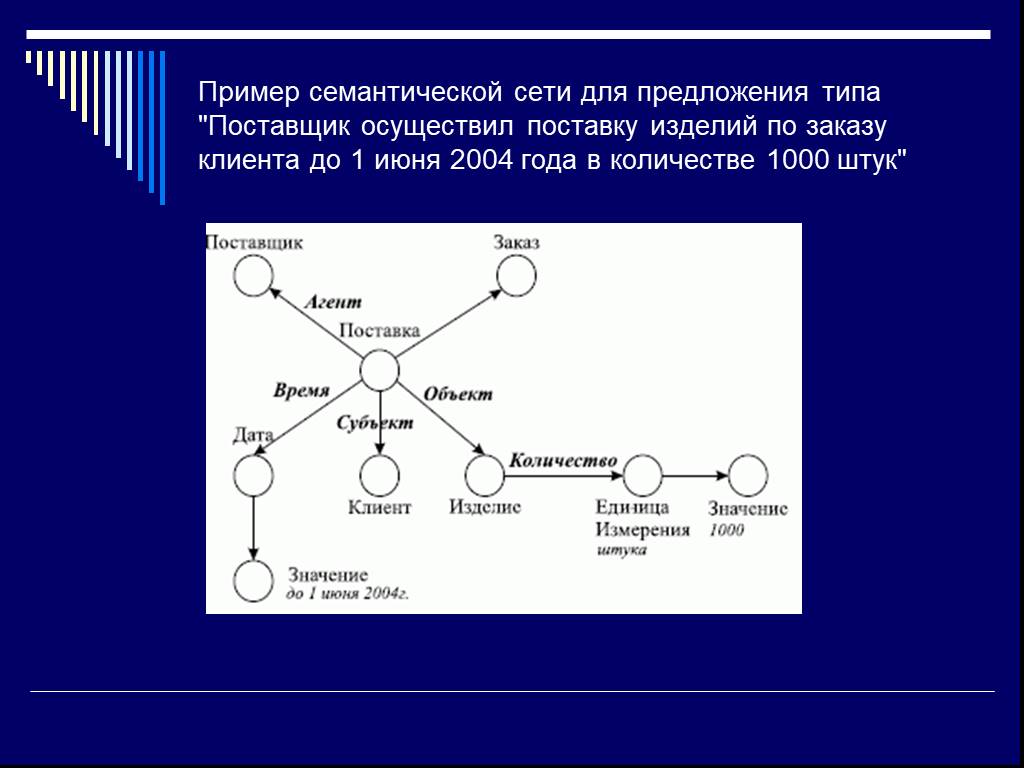
Пример семантической сети для предложения типа "Поставщик осуществил поставку изделий по заказу клиента до 1 июня 2004 года в количестве 1000 штук"

Число отношений, используемых в конкретных семантических сетях, может быть разное.

Неполный список возможных отношений, используемых в семантических сетях для разбора предложений: Агент - это то, что (тот, кто) вызывает действие. Агент часто является подлежащим в предложении, например, "Робби ударил мяч". Объект - это то, на что (на кого) направлено действие. В предложении объект часто выполняет роль прямого дополнения, например, "Робби взял желтую пирамиду ". Инструмент - то средство, которое используется агентом для выполнения действия, например, "Робби открыл дверь с помощью ключа ". Соагент служит как подчиненный партнер главному агенту, например, "Робби собрал кубики с помощью Суззи". Пункт отправления и пункт назначения - это отправная и конечная позиции при перемещении агента или объекта: "Робби перешел из комнаты в библиотеку ". Траектория - перемещение от пункта отправления к пункту назначения: "Они прошли через дверь по ступенькам на лестницу ". Средство доставки - то в чем или на чем происходит перемещение: "Он всегда едет домой на метро ". Местоположение - то место, где произошло (происходит, будет происходить) действие, например, "Он работал за столом ". Потребитель - то лицо, для которого выполняется действие: "Робби собрал кубики для Суззи". Сырье - это, как правило, материал, из которого что-то сделано или состоит. Обычно сырье вводится предлогом из, например, "Робби собрал Суззи из интегральных схем ". Время - указывает на момент совершения действия: "Он закончил свою работу поздно вечером ".

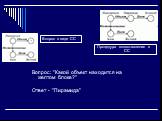
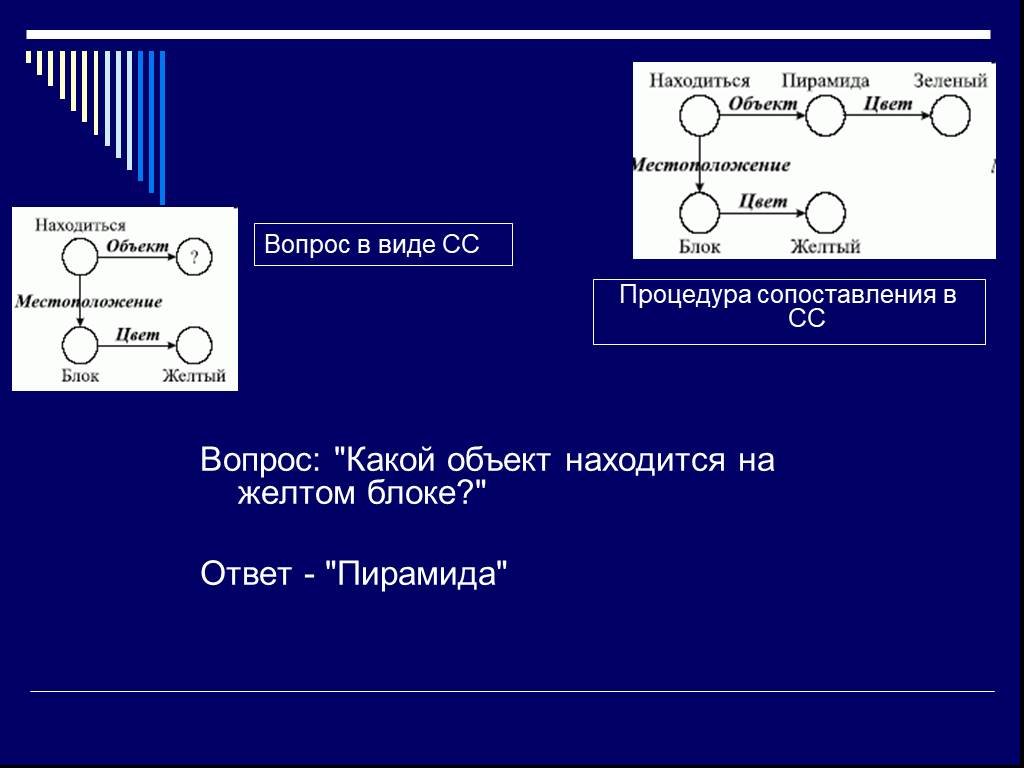
Вопрос: "Какой объект находится на желтом блоке?" Ответ - "Пирамида"

Процедура сопоставления в СС

Вопрос в виде CC

Фреймовые модели

предложены в 1975 году Марвином Минским. Фрейм (рамка в переводе с англ.) - это единица представления знаний, запомненная в прошлом, детали которой могут быть изменены согласно текущей ситуации. Фрейм представляет собой структуру данных, с помощью которых можно, например, описать обстановку в комнате или место встречи для проведения совещания. М.Минский предлагал эту модель для описания пространственных сцен. Однако с помощью фреймов можно описать ситуацию, сценарий, роль, структуру и т.д.

Фрейм

отражает основные свойства объекта или явления. Структура фрейма записывается в виде списка свойств, называемых во фрейме слотами. :{(Ai, vi)},{ri} Ai – имя признака, vi – его значения ,ri – связь с другими слотами. Рассмотрим запись фрейма на языке FRL (Frame Representation Language) - языке, похожем на LISP, но только внешне из-за наличия скобок. Например, фрейм СТОЛ может быть записан в виде 3 слотов: слот НАЗНАЧЕНИЕ (purpose), слот ТИП (type) и слот ЦВЕТ (color) следующим образом: (frame СТОЛ (purpose (value(размещение предметов для деятельности рук))) (type (value(письменный))) (color (value (коричневый))))

Во фрейме СТОЛ представлены только ДЕКЛАРАТИВНЫЕ средства для описания объекта, и такой фрейм носит название фрейм-образец. Однако существуют также фреймы-экземпляры, которые создаются для отображения фактических ситуаций на основе поступающих данных и ПРОЦЕДУРАЛЬНЫХ средств (демонов), например, следующих: IF-DEFAULT - по умолчанию IF-NEEDED - если необходимо IF-ADDED - если добавлено IF-REMOVED - если удалено

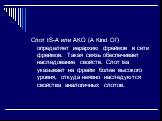
Слот IS-A или AKO (A Kind Of) определяет иерархию фреймов в сети фреймов. Такая связь обеспечивает наследование свойств. Слот isa указывает на фрейм более высокого уровня, откуда неявно наследуются свойства аналогичных слотов.

Рассмотрим фрагмент описания из "мира блоков" в виде фреймов.

(frame (name (Cube)) (isa (Block World)) (length (NULL)) (width (IF-DEFAULT (use length))) (height (IF-DEFAULT (use length)))) (frame (name (B1)) (isa (Cube)) (color (red)) (length (80))) (frame (name (B2)) (isa (Cube)) (color (green)) (length (65)) (who_put (value (NULL)) (IF_NEEDED (askuser))))

Слот isa указывает на то, что объекты B1 и B2 являются подтипом объекта Cube и наследуют его свойства, а именно, length = width = height. Демон IF_NEEDED запускается автоматически, если понадобится узнать, кто поставил B2 на стол. Полученный ответ (Робби) будет подставлен в значение слота who_put. Аналогично работают демоны IF-ADDED и IF-REMOVED.

Допустим, однорукому роботу Робби дается приказ "Возьми желтый предмет, который поддерживает пирамиду". На языке представления знаний (ЯПЗ) вопрос записывается так: (object ? X (color (yellow)) (hold ? Y (type (pyramid))))

Программа сопоставления с образцом находит в базе знаний описание объектов: (frame (name (B3)) (type (block)) (color (yellow)) (size (20 20 20)) (coordinate (20 50 0)) (hold (P2))) и (frame (name (P2)) (type (pyramid)) ...) Ответ получен X = B3, Y = P2 и Робби выдается команда take(object=B3)

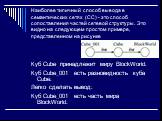
Наиболее типичный способ вывода в семантических сетях (СС) - это способ сопоставления частей сетевой структуры. Это видно на следующем простом примере, представленном на рисунке

Куб Cube принадлежит миру BlockWorld. Куб Cube_001 есть разновидность куба Cube. Легко сделать вывод: Куб Cube_001 есть часть мира BlockWorld.

Каждый фрейм можно рассматривать как семантическую сеть, состоящую из выделенных вершин и связей

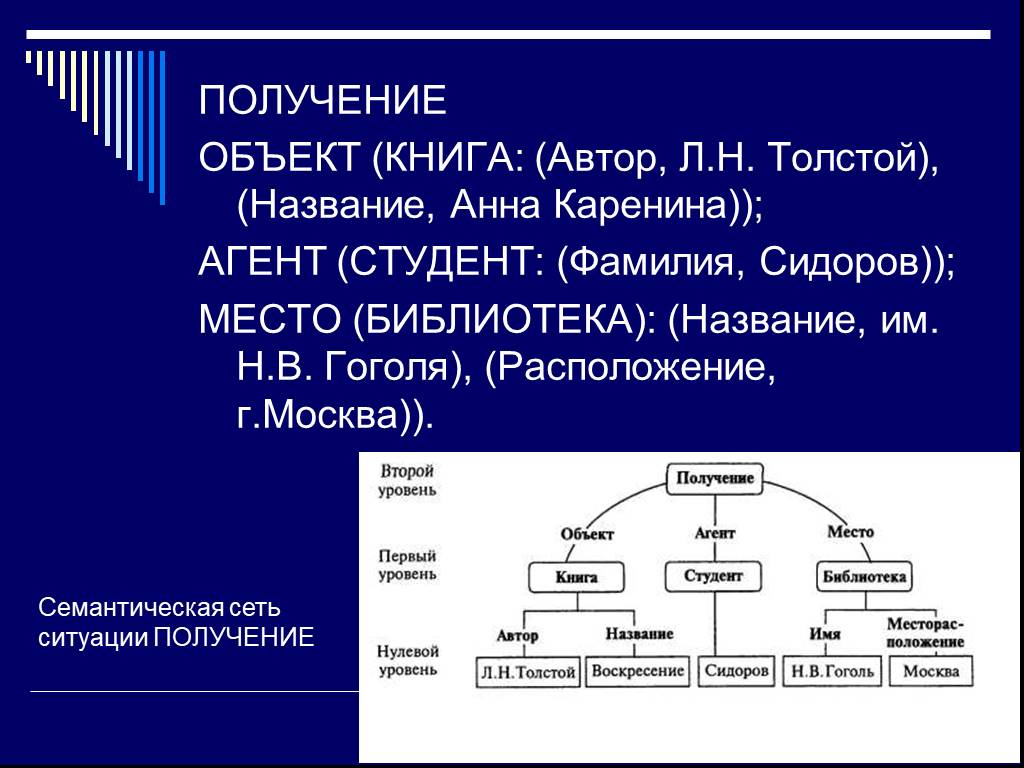
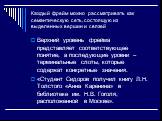
Верхний уровень фрейма представляет соответствующее понятие, а последующие уровни – терминальные слоты, которые содержат конкретные значения. «Студент Сидоров получил книгу Л.Н. Толстого «Анна Каренина» в библиотеке им. Н.В. Гоголя, расположенной в Москве».

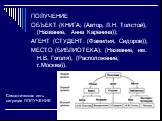
ПОЛУЧЕНИЕ ОБЪЕКТ (КНИГА: (Автор, Л.Н. Толстой), (Название, Анна Каренина)); АГЕНТ (СТУДЕНТ: (Фамилия, Сидоров)); МЕСТО (БИБЛИОТЕКА): (Название, им. Н.В. Гоголя), (Расположение, г.Москва)).

Семантическая сеть ситуации ПОЛУЧЕНИЕ

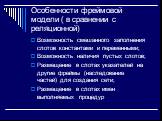
Особенности фреймовой модели ( в сравнении с реляционной)

Возможность смешанного заполнения слотов константами и переменными; Возможность наличия пустых слотов; Размещение в слотах указателей на другие фреймы (наследование частей) для создания сети; Размещение в слотах имен выполняемых процедур

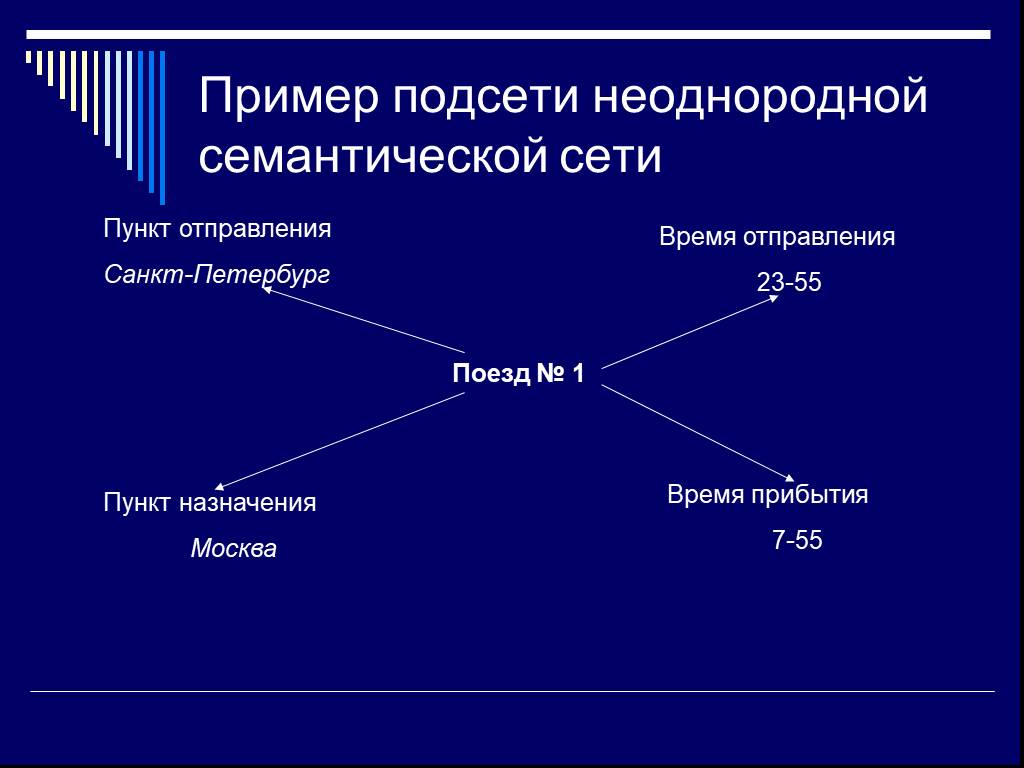
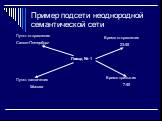
Пример подсети неоднородной семантической сети

Поезд № 1

Пункт отправления Санкт-Петербург

Время отправления 23-55

Пункт назначения Москва

Время прибытия 7-55

Фрейм-прототип - фрейм, у которого значения всех или части слотов являются переменными ПО. Фрейм-экземпляр (или фрейм-пример) – фрейм, у которого значения всех слотов являются константами

При представлении таблицы в виде фрейма поля записи называются его слотами. Таблица содержит имена и значения слотов, а ее название трактуется как имя фрейма

Процедурные модели представления данных

К типовым процедурным моделям представления знаний относятся логические модели, реализуемые на языках алгебры логики (исчисления высказываний и предикатов), продукционные модели.

Исчисления предикатов

Под исчислением предикатов понимается формальный язык для представления отношений в некоторой предметной области. Предикатом называют предложение, принимающее только два значения: "истина" или "ложь". Для обозначения предикатов применяются логические связки между высказываниями: ¬ - не, V- или,  - и,  - если, а также квантор существования  и квантор всеобщности  .

 x(...) - существует такой x, что ...  x(...) - для любого x Таким образом, логика предикатов оперирует логическими связками между высказываниями, например, она решает вопросы: можно ли на основе высказывания A получить высказывание B и т.д.

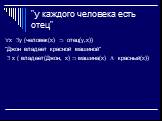
"у каждого человека есть отец"

x y (человек(x)  отец(y,x)) "Джон владеет красной машиной"  x ( владеет(Джон, x)  машина(x)  красный(x))

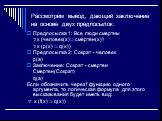
Рассмотрим вывод, дающий заключение на основе двух предпосылок:

Предпосылка 1: Все люди смертны x (человек(x) смертен(x)) x (p(x)  q(x)) Предпосылка 2: Сократ - человек p(a) Заключение: Сократ - смертен Смертен(Сократ) q(a) Если обозначить через f функцию одного аргумента, то логическая формула для этого высказывания будет иметь вид:  x (f(x)  q(x))

Алфавит логики предикатов

состоит из элементов (символов): x, y, z, u, v, w - переменные; a, b, c, d, e - константы; f, g, h - функциональные символы; p, q, r, s, t - предикатные символы; ¬, , V, ,, - логические символы. y  x (человек(x)  отец(y,x)) "у всех людей общий отец".

Даны следующие факты:

"Иван является отцом Михаила" - отец(a,b) "Петр является отцом Василия" - отец(c,d) "Иван и Петр являются братьями" – w (брат(a,c)  отец(w,a)  отец(w,c))

Даны следующие определения:

"Брат отца является дядей" - y (дядя(x,u)  отец(y,u)  брат(y,x)) "Сын дяди является двоюродным братом" -  x (дв.брат(z,u)  дядя(x,u)  отец(x,z)) Требуется доказать, что "Михаил и Василий являются двоюродными братьями": x  y (дв.брат(b,d)  отец(y,b)  брат (y,x)  отец(x,d)) Делаем подстановки y = Иван, b = Михаил и x = Петр, d = Василий, видим, что предикаты 1, 2, 3 дают правильное предложение 6.

Рассмотренный нами язык называется исчислением предикатов первого порядка и позволяет связывать знаком квантора переменные, соответствующие объектам из предметной области, но не предикаты или функции. Исчисление предикатов второго порядка позволяет связывать знаком квантора не только переменные, соответствующие объектам из предметной области, но и предикаты или функции. Примером исчисления предикатов второго порядка может служить выражение "Единственное качество Джона - это честность", которое записывается так: P (P(Джон)  качество(P)  P = честность)

Системы продукций

Под продукцией будем понимать выражение: Если то , где: Xi,Yi - логические выражения, Di - фактор достоверности (0,1) или фактор уверенности (0,100).

это набор правил, используемый как база знаний, поэтому его еще называют базой правил. продукции соответствуют навыкам решения задач человеком в долгосрочной памяти человека. Подобно навыкам в долгосрочной памяти эти продукции не изменяются при работе системы. Они вызываются по "образцу" для решения данной специфической проблемы. Рабочая память продукционной системы соответствует краткосрочной памяти, или текущей области внимания человека. Содержание рабочей области после решения задачи не сохраняется.

Работа продукционной системы

инициируется начальным описанием (состоянием) задачи. Из продукционного множества правил выбираются правила, пригодные для применения на очередном шаге. Эти правила создают так называемое конфликтное множество. Для выбора правил из конфликтного множества существуют стратегии разрешения конфликтов, которые могут быть и достаточно простыми, например, выбор первого правила, а могут быть и сложными эвристическими правилами. Продукционная модель в чистом виде не имеет механизма выхода из тупиковых состояний в процессе поиска. Она продолжает работать, пока не будут исчерпаны все допустимые продукции. Практические реализации продукционных систем содержат механизмы возврата в предыдущее состояние для управления алгоритмом поиска.

Пример использования продукционных систем

для решения шахматной задачи хода конем в упрощенном варианте на доске размером 3 x 3. Требуется найти такую последовательность ходов конем, при которой он ставится на каждую клетку только один раз. Записанные на рисунке предикаты move(x,y) составляют базу знаний (базу фактов) для задачи хода конем. Продукционные правила - это факты перемещений move, первый параметр которых определяет условие, а второй параметр определяет действие (сделать ход в поле, в которое конь может перейти).

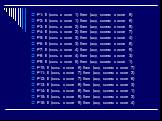
P1: If (конь в поле 1) then (ход конем в поле 8) P2: If (конь в поле 1) then (ход конем в поле 6) P3: If (конь в поле 2) then (ход конем в поле 9) P4: If (конь в поле 2) then (ход конем в поле 7) P5: If (конь в поле 3) then (ход конем в поле 4) P6: If (конь в поле 3) then (ход конем в поле 8) P7: If (конь в поле 4) then (ход конем в поле 9) P8: If (конь в поле 4) then (ход конем в поле 3) P9: If (конь в поле 6) then (ход конем в поле 1) P10: If (конь в поле 6) then (ход конем в поле 7) P11: If (конь в поле 7) then (ход конем в поле 2) P12: If (конь в поле 7) then (ход конем в поле 6) P13: If (конь в поле 8) then (ход конем в поле 3) P14: If (конь в поле 8) then (ход конем в поле 1) P15: If (конь в поле 9) then (ход конем в поле 2) P16: If (конь в поле 9) then (ход конем в поле 4)

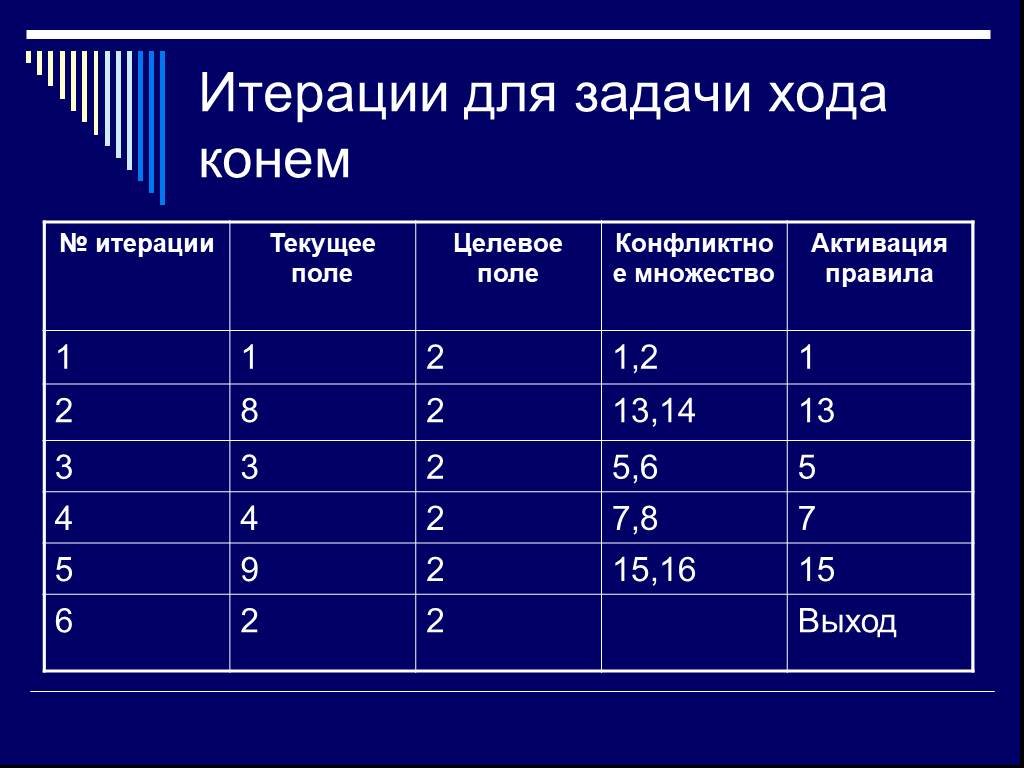
Итерации для задачи хода конем

Продукционные системы могут порождать бесконечные циклы при поиске решения. В продукционной системе эти циклы особенно трудно определить, потому что правила могут активизироваться в любом порядке. Например, если в 4-й итерации выбирается правило 8, мы попадаем в поле 3 и зацикливаемся. Самая простая стратегия разрешения конфликтов сводится к тому, чтобы выбирать первое соответствующее перемещение, которое ведет в еще не посещаемое состояние. Следует также отметить, что конфликтное множество это простейшая база целей.

Основные преимущества продукционных систем:

простота и гибкость выделения знаний; отделение знаний от программы поиска; модульность продукционных правил (правила не могут "вызывать" другие правила); возможность эвристического управления поиском; возможность трассировки "цепочки рассуждений"; независимость от выбора языка программирования; продукционные правила являются правдоподобной моделью решения задачи человеком.

Нечеткая логика

При формализации знаний достаточно часто встречаются качественные знания, например, высокая температура при гриппе, слабое свечение нити накаливания, молодой дипломат и т.д. Для формального представления таких качественных знаний американский математик, профессор информатики в Университете в Беркли (Калифорния) Лофти А.Заде (Иран) предложил в 1965 году формальный аппарат нечеткой (fuzzy) логики

Нечеткое подмножество N множества M определяется как множество упорядоченных пар N = {μN(x)/x}, где μN(x) - характеристическая функция принадлежности (или просто функция принадлежности), принимающая значения в интервале [0, 1] и указывающая степень (или уровень) принадлежности элемента x подмножеству N. Таким образом, нечеткое множество N можно записать как

где Xi - i-е значение базовой шкалы, а знак "+" не является обозначением операции сложения, а имеет смысл объединения.

Определим лингвистическую переменную (ЛП) как переменную, значение которой определяется набором словесных характеристик некоторого свойства. Например, ЛП "возраст" может иметь значения ЛП = МлВ, ДВ, ОВ, ЮВ, МВ, ЗВ, ПВ, СВ , обозначающие возраст младенческий, детский, отроческий, юношеский, молодой, зрелый, преклонный и старый, соответственно. Множество M - это шкала прожитых человеком лет [0..120]. Функция принадлежности определяет, насколько мы уверены, что данное количество прожитых лет можно отнести к данному значению ЛП. Допустим, что неким экспертом к молодому возрасту отнесены люди в возрасте 20 лет со степенью уверенности 0,8, в возрасте 25 лет со степенью уверенности 0,95, в возрасте 30 лет со степенью уверенности 0,95 и в возрасте 35 лет со степенью уверенности 0,7. Итак: μ(X1)=0,8; μ(X2)=0,95; μ(X3)=0,95; μ(X4)=0,7;

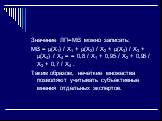
Значение ЛП=МВ можно записать: МВ = μ(X1) / X1 + μ(X2) / X2 + μ(X3) / X3 + μ(X4) / X4 = = 0,8 / X1 + 0,95 / X2 + 0,95 / X3 + 0,7 / X4 . Таким образом, нечеткие множества позволяют учитывать субъективные мнения отдельных экспертов.

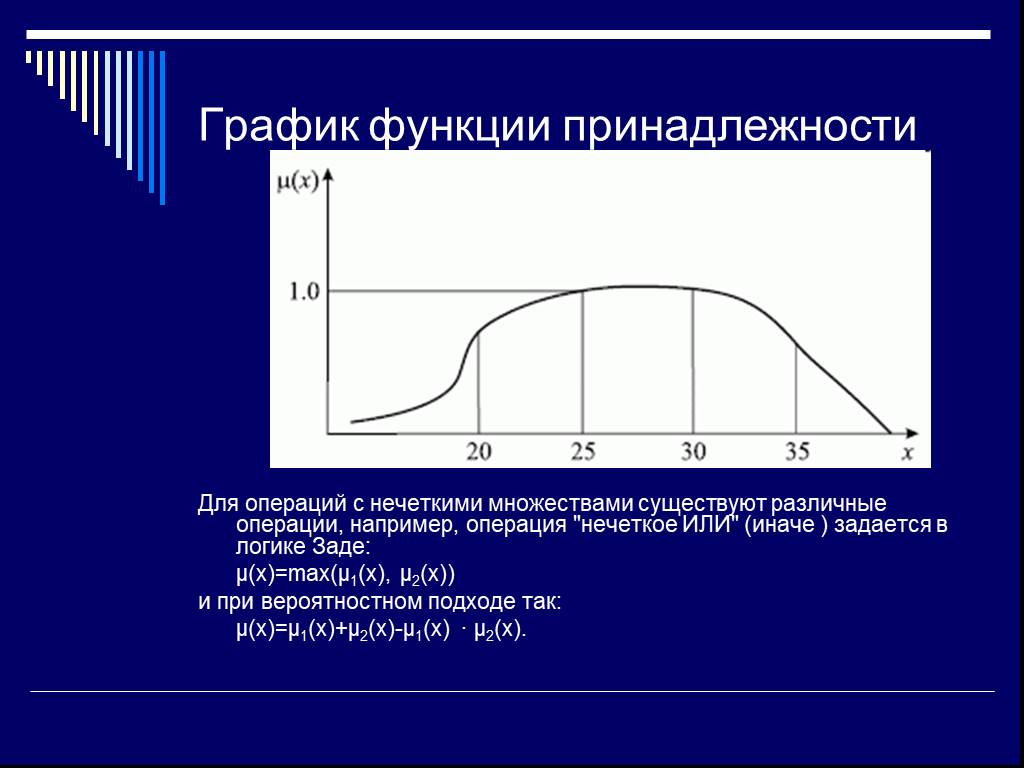
График функции принадлежности

Для операций с нечеткими множествами существуют различные операции, например, операция "нечеткое ИЛИ" (иначе ) задается в логике Заде: μ(x)=max(μ1(x), μ2(x)) и при вероятностном подходе так: μ(x)=μ1(x)+μ2(x)-μ1(x) · μ2(x).

Нечеткие множества

(другое название - мягкие вычисления) очень часто применяются в экспертных системах. Нечеткая логика применяется как удобный инструмент для управления технологическими и индустриальными процессами, для интеллектуального домашнего хозяйства и электроники развлечения, в системах обнаружения ошибок и других экспертных системах. Разработаны специальные средства нечеткого вывода, например, инструментальное средство Fuzzy CLIPS. Нечеткая логика была изобретена в Соединенных Штатах, и сейчас быстрый рост этой технологии начался в Японии, Европе и теперь снова достиг США. Развитием этого направления является реализации в системах представления знаний НЕ-факторов: неполнота, неточность, недоопределенность, неоднозначность, некорректность и др