Презентация "Гармонические колебания и маятники" по физике – проект, доклад
Презентацию на тему "Гармонические колебания и маятники" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 61 слайд(ов).
Слайды презентации
Список похожих презентаций
Гармонические колебания точки
Цели урока:. Систематизировать знания о свойствах тригонометрических функций. Продолжить формирование умений преобразования графиков тригонометрических ...Гармонические колебания
Давайте вспомним. Колебания – … процесс, который частично или полностью повторяется через некоторый промежуток времени. Например, …. Амплитуда- … ...Электромагнитные гармонические колебания
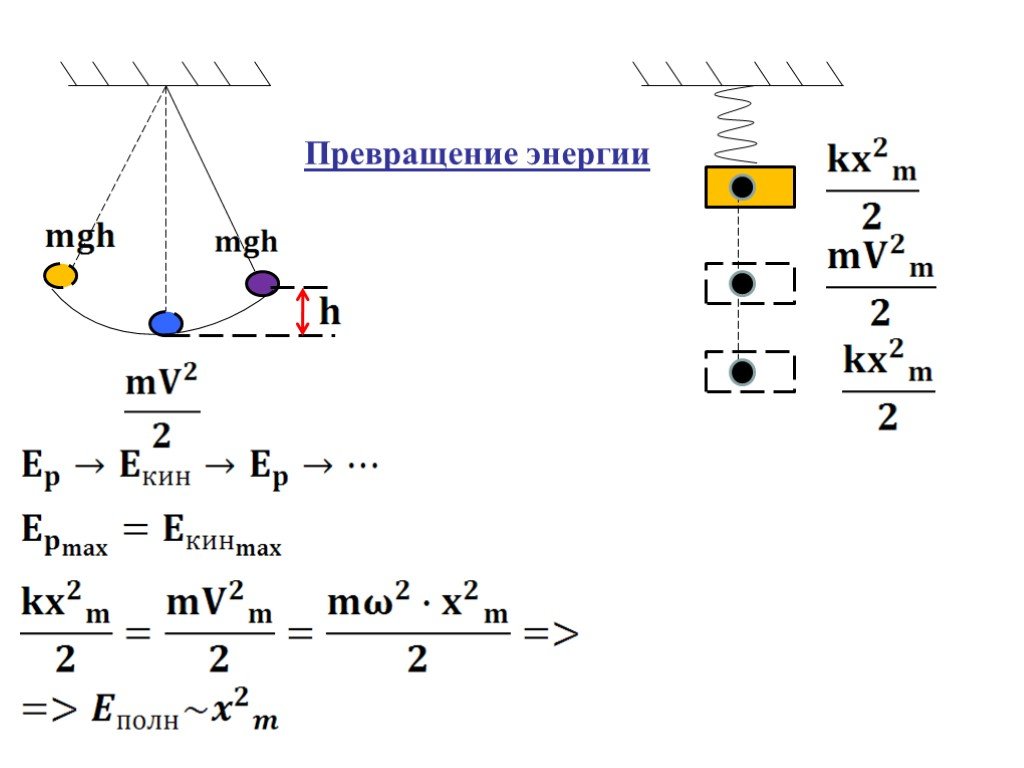
Цель учебная: Сформировать у студентов понятие «гармоническое колебание» и научить определять параметры колебаний математическими способами. Задачи ...Превращение энергии при колебательном движении. Затухающие колебания
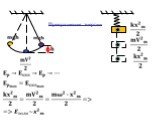
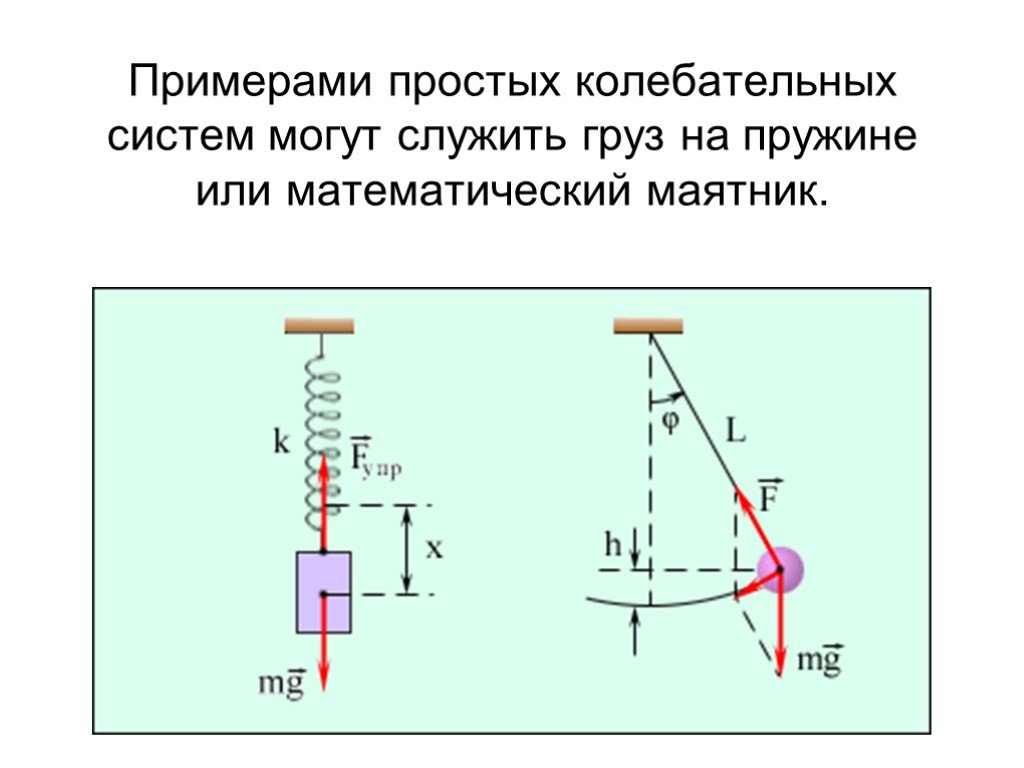
Для любого промежуточного положения на пути ВО сумма потенциальной и кинетической энергии есть постоянная величина, равная первоначальному запасу ...Механические колебания и звуковые волны
Механические колебания – это системы, которые могут совершать колебательные движения. Примеры механического колебания:. Механические колебания. Гармонические ...Механические колебания и волны. Акустика
Периодические механические процессы в живом организме. Колебания – это процессы повторяющиеся во времени. При этом система многократно отклоняется ...Механические колебания и волны
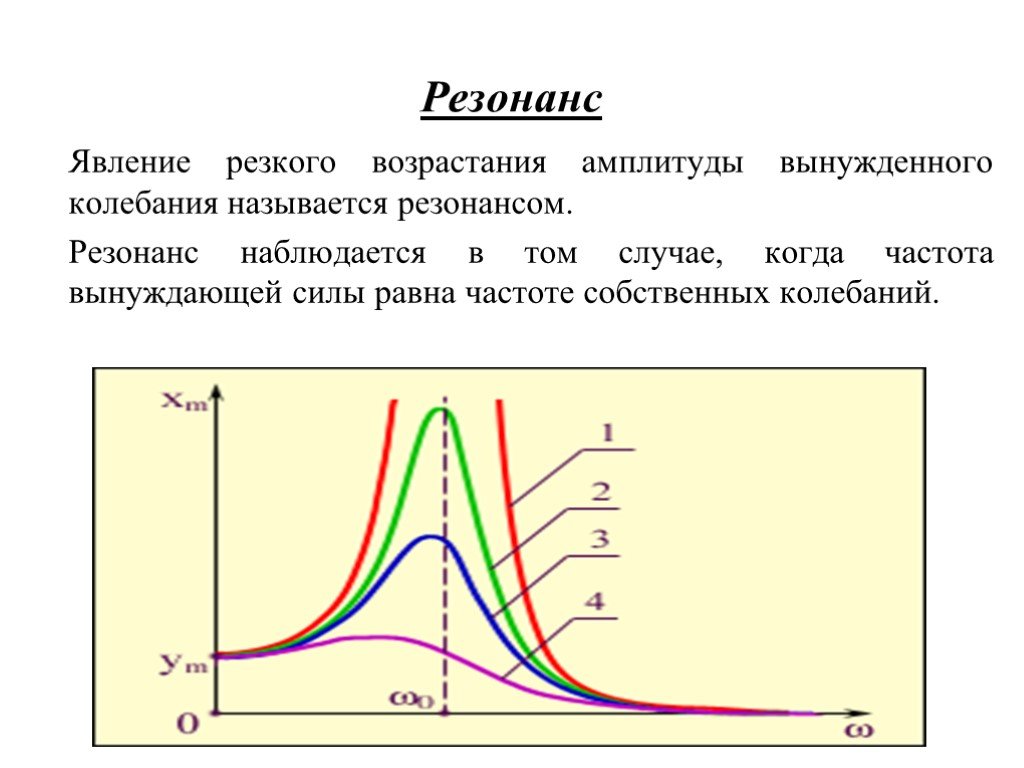
Механические колебания и волны. Механические колебания. Виды колебаний Затухающие колебания – это колебания, амплитуда которых, под действием сил ...Вынужденные колебания резонанс
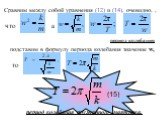
Значение. Явление резкого возрастания амплитуды вынужденных колебаний тока в колебательном контуре, которое происходит при совпадении частоты вынужденных ...Электромагнитные колебания и волны
Из истории. Существование электромагнитных волн было предсказано М. Фарадеем в 1832. Дж. Максвелл в 1865г. теоретически показал, что электромагнитные ...Электромагнитные колебания
О, сколько нам открытий чудных Готовят просвещения дух И опыт, сын ошибок трудных, И гений, парадоксов друг, И случай, бог изобретатель. А. С. Пушкин. ...Звуковые колебания
АКУСТИКА- РАЗДЕЛ ФИЗИКИ, В КОТОРОМ ИЗУЧАЮТСЯ ЗВУКОВЫЕ ЯВЛЕНИЯ. Источники звука. Звук создается коротким или долгим колебанием каких-то предметов. ...Звуковые колебания
Колизей (80-90 гг. н.э.). Мавзолей, получивший название Гол Гумбаз. Построен в 1659 году. Собор Св. Петра. Реверберация — это отражение звука от различных ...Затухающие колебания
. Рис. 26.1. Выясним физический смысл и Обозначим через -время, в течение которого амплитуда А уменьшается в e раз. A0 /AΊ = e = e1, откуда ...Вынужденные электромагнитные колебания
Вынужденными электромагнитными колебаниями называют периодические изменения силы тока и напряжения в электрической цепи, происходящие под действием ...Свободные электромагнитные колебания
Электромагнитные колебания — это колебания электрических и магнитных полей, которые сопровождаются периодическим изменением заряда, тока и напряжения. ...Физика механические колебания
Когда приютит задремавшее стадо Семейство берез на холме за рекой, Пастух, наблюдая игру листопада, Лениво сидит и болтает ногой. Николай Рубцов. ...Звуковые колебания
Определение. Упругие волны, продольно распространяющиеся в среде и создающие в ней механические колебания. Звуки музыкальных инструментов. Звуки гитары ...Электромагнитные колебания
Определение. Электромагнитные колебания – это периодические или почти периодические изменения заряда, силы тока и напряжения. Колебания происходят ...Звуковые колебания
План урока. Повторение опорных знаний Объяснение нового материала Закрепление изученного материала Домашнее задание. Повторение кроссворд. Возмущения, ...Электромагнитные колебания решение задач
Решение задач на тему «ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ». Заряд q изменяется с течением времени t в соответствии с уравнением q=2*10-6соs104 πt. Записать ...Конспекты
Электромагнитные колебания
11 класс. Урок. . Тема :. «Электромагнитные колебания». Цель:. Продолжить формирование умений решения задач. по электромагнитным колебаниям. ...Свободные и вынужденные колебания
ПЛАН-КОНСПЕКТ УРОКА __________________________________________. Свободные и вынужденные колебания. . ФИО (полностью). . Шалотенко Лариса ...Свободные механические колебания
Мальцева Людмила Анатольевна,. учитель физики,. первая квалификационная категория. муниципальное бюджетное общеобразовательное учреждение. ...Обобщение и систематизация знаний по теме «Механические колебания и волны
. МБОУ «Клюквинская средняя общеобразовательная школа». Открытый урок по физике в 9 классе на тему«Обобщение и систематизация ...Периодические движения: равномерное вращение по окружности и колебания
Урок – Повторение по теме: "Периодические движения: равномерное вращение по окружности и колебания". Воронкова Екатерина Валерьевна. учитель физики, ...Механические колебания и волны. Звук
9 класс. Повторительно-обобщающий урок. . «Механические колебания и волны. Звук». Цели урока:. Повторить, обобщить и оценить знания учащихся ...Механические колебания и волны. Звук
Урок – соревнование в 9 классе по теме :. «Механические колебания и волны. Звук.». Тип урока:. повторительно – обобщающий . Форма урока:. ...Механические колебания и волны. Звук
Муниципальное общеобразовательное учреждение. . «Средняя общеобразовательная школа с. Агафоновка. . Питерского района Саратовской области». ...Механические колебания и волны. Звук
ОГОУ СПО. . "Белгородский механико-технологический колледж". Методическая разработка. урока по физике. . ...Механические колебания и волны
Механические колебания и волны. Урок обобщения в 9 классе. Цели урока:. . . обобщить, закрепить знания учащихся по данной теме, совершенствовать ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 декабря 2018
Категория:Физика
Содержит:61 слайд(ов)
Поделись с друзьями:
Скачать презентацию









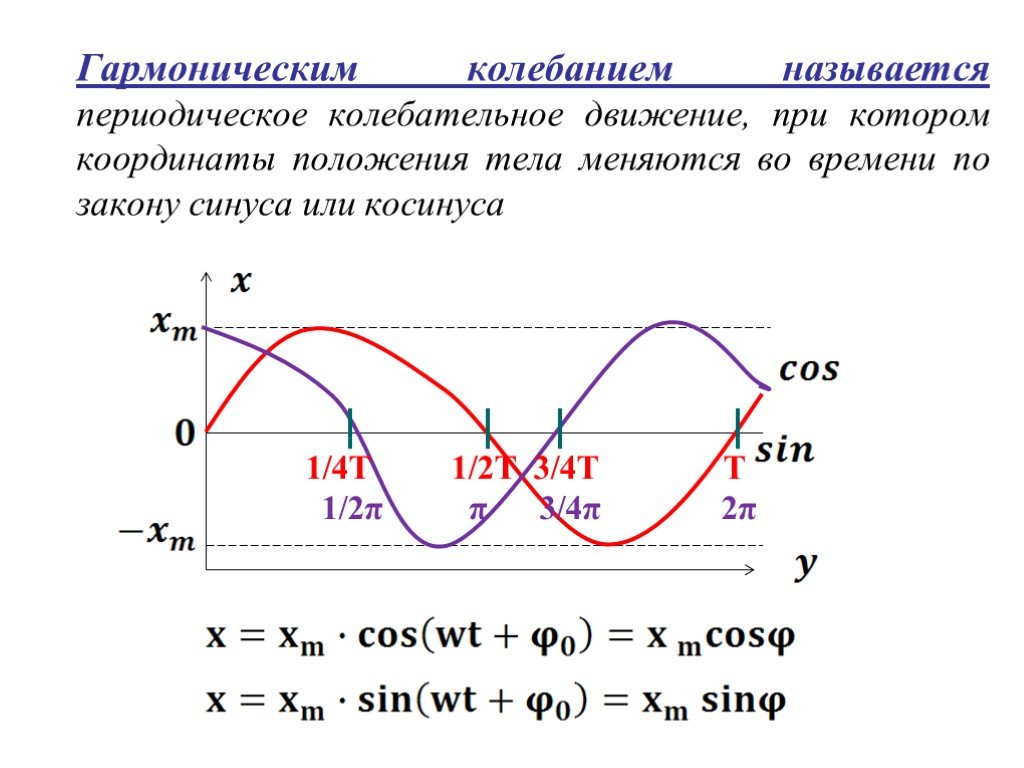

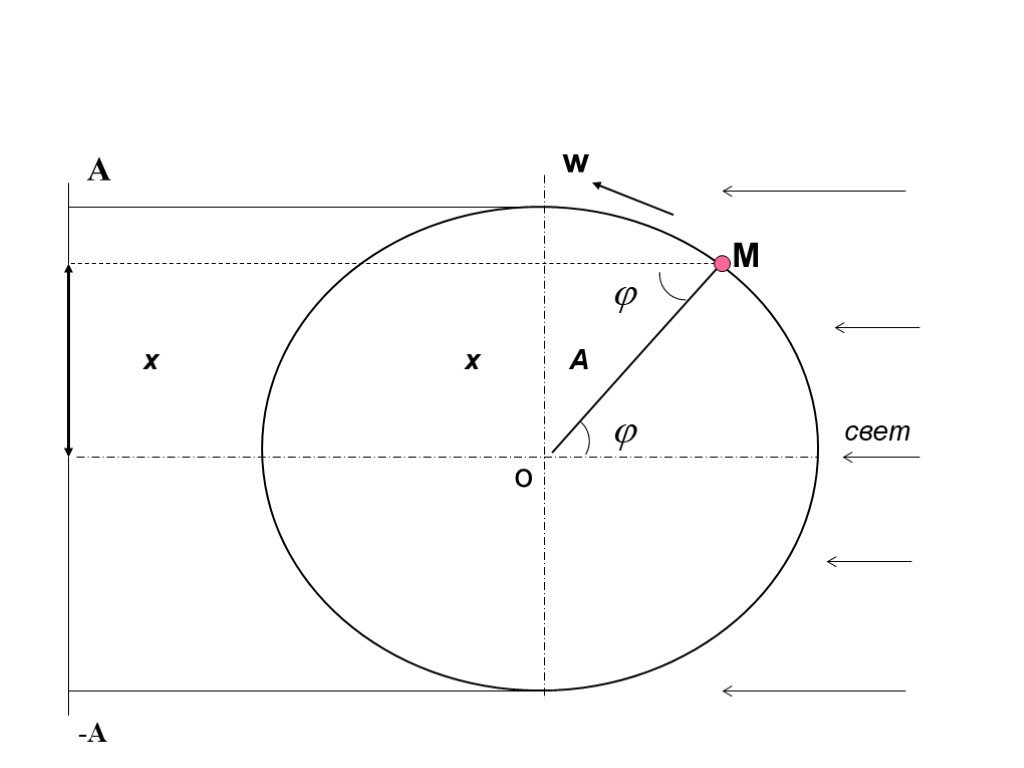

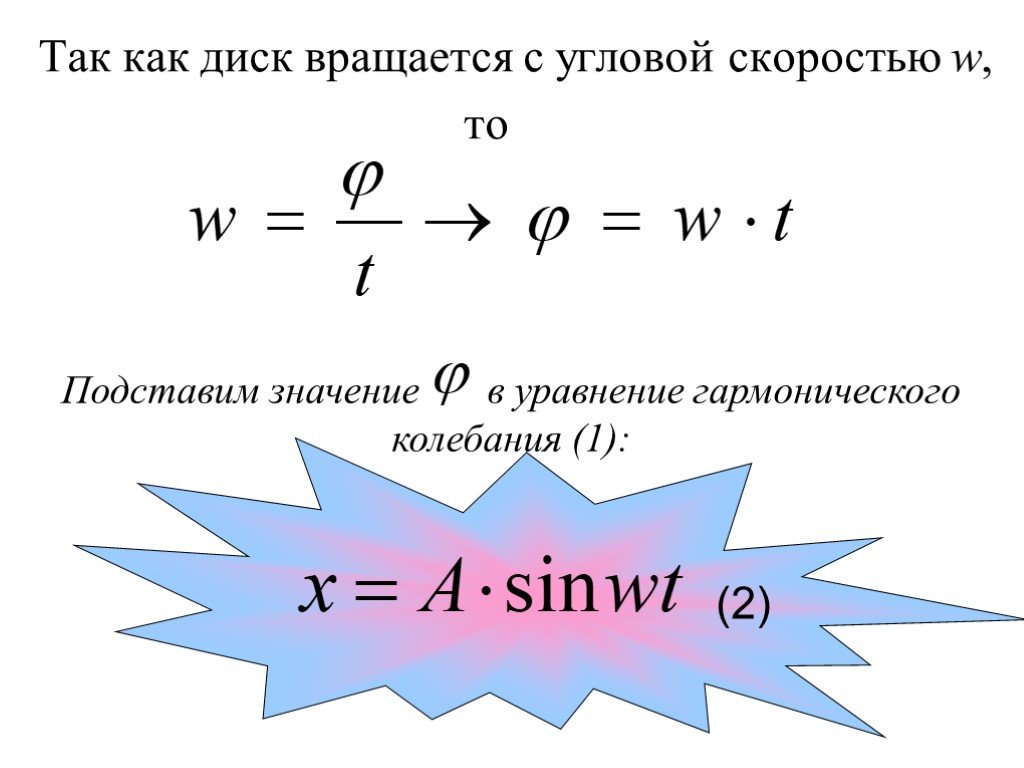
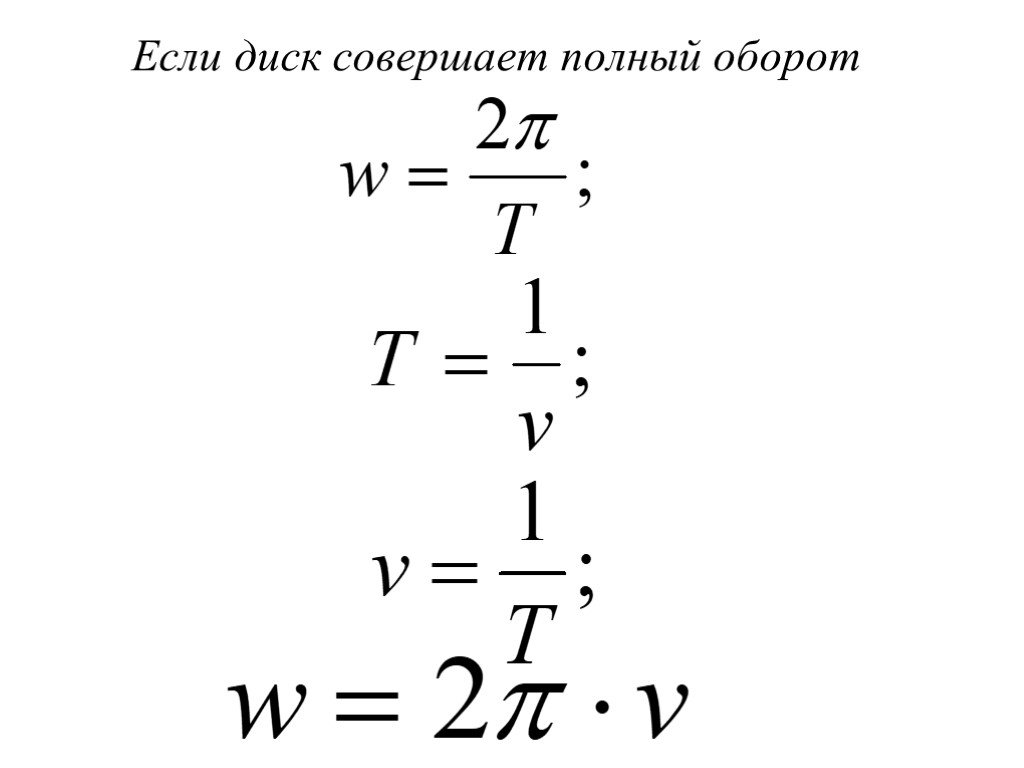


















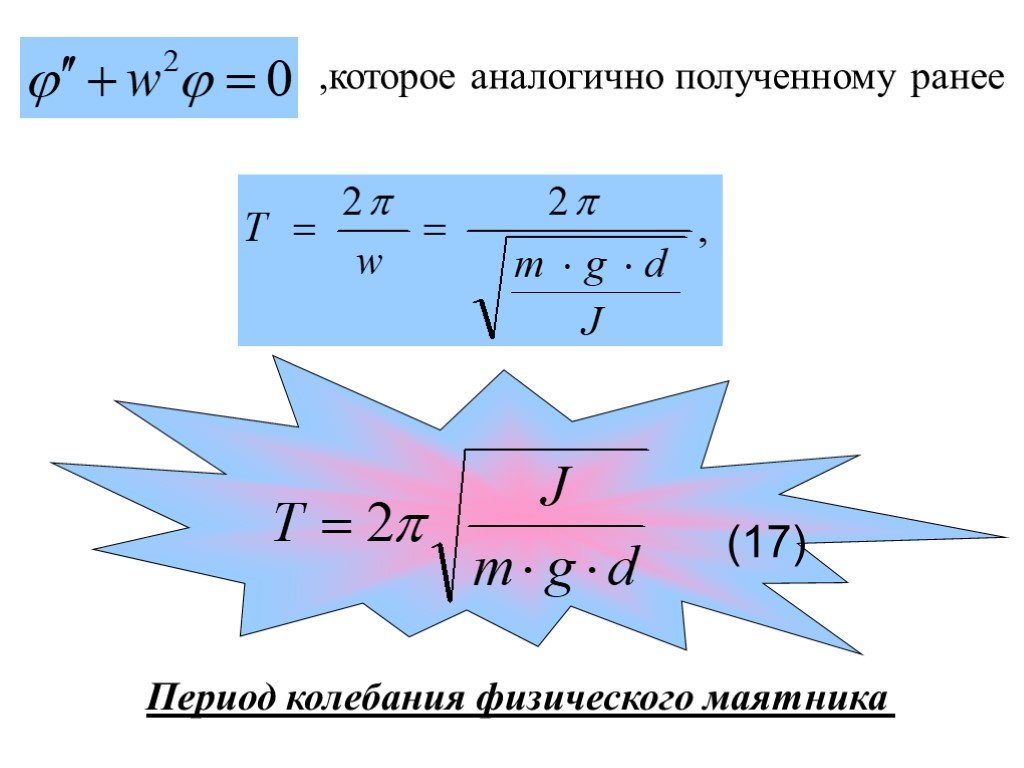
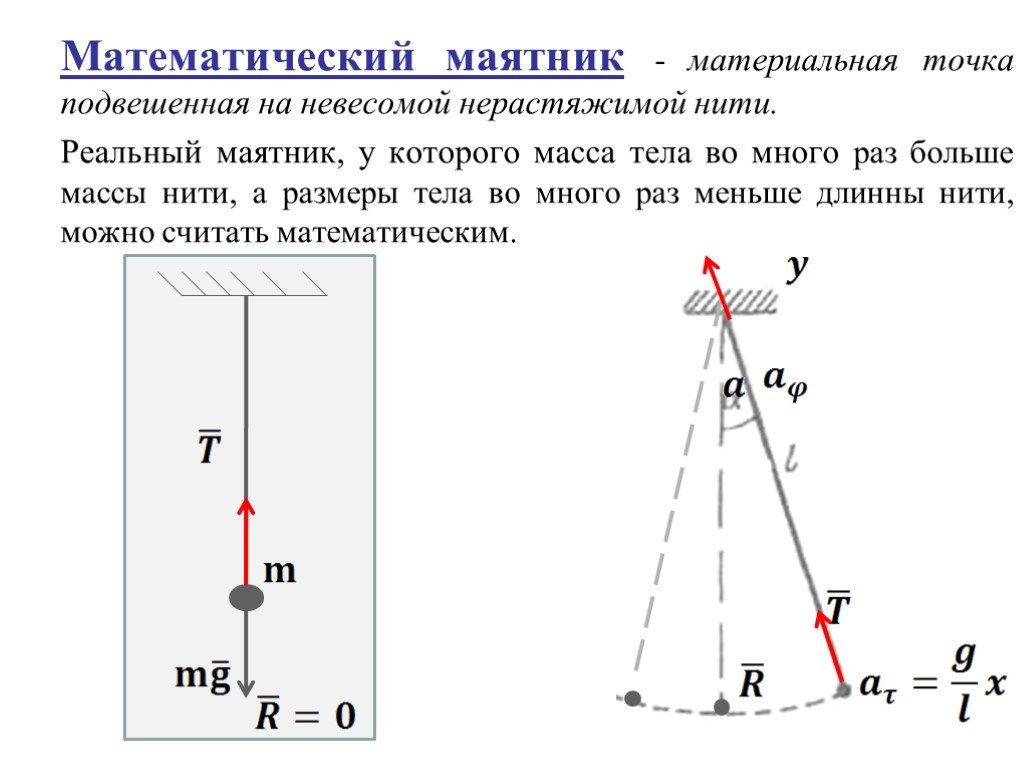
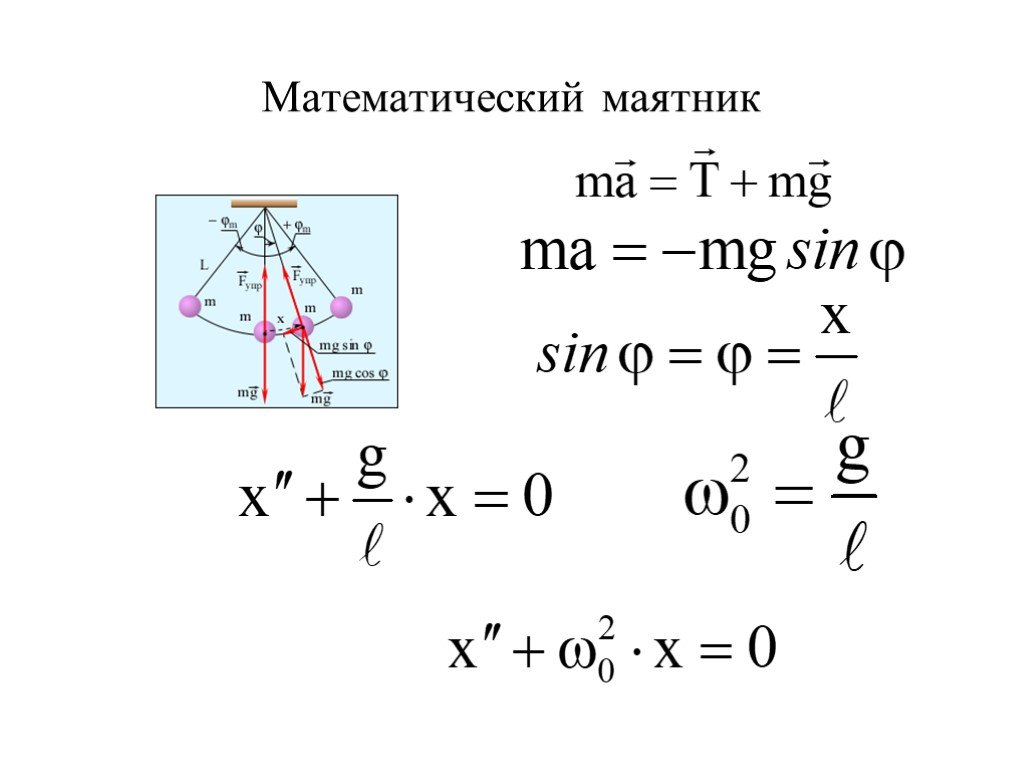

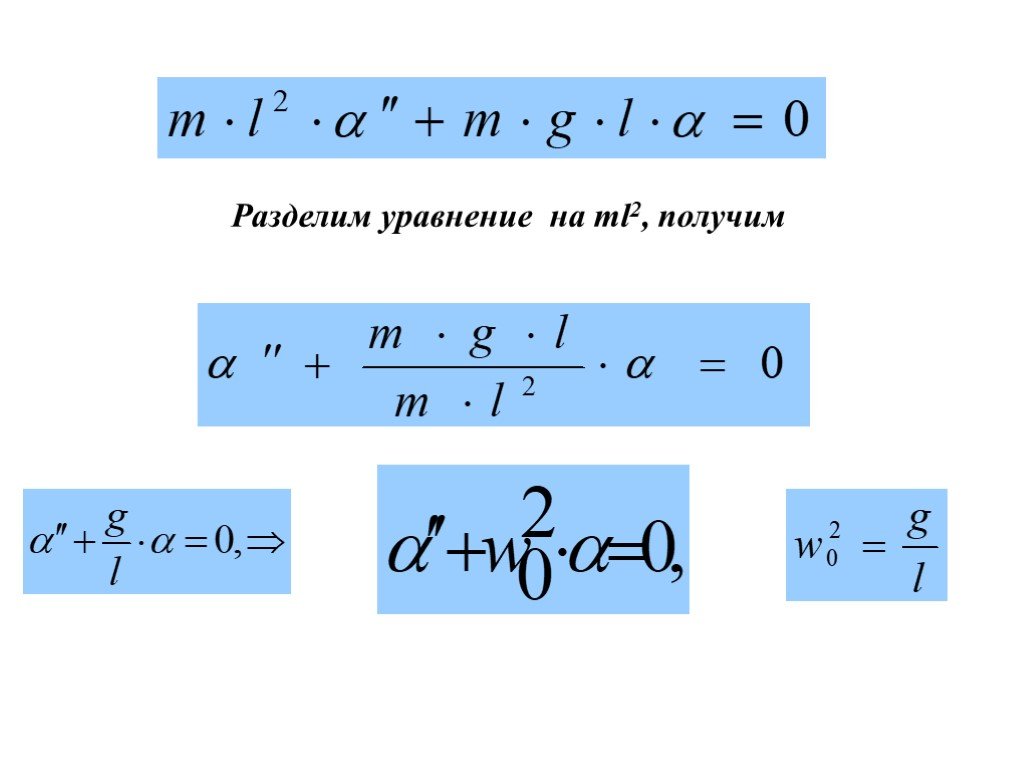


























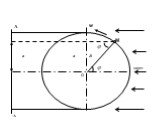

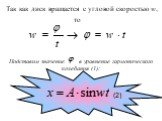

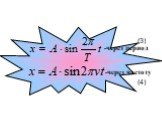

![w – циклическая частота - число полных колебаний за 2π сек,[рад/с] 5. wt- фаза колебания - характеризует состояние колебательной системы в любой заданный момент времени. 6. v- частота- число колебаний в единицу времени. w – циклическая частота - число полных колебаний за 2π сек,[рад/с] 5. wt- фаза колебания - характеризует состояние колебательной системы в любой заданный момент времени. 6. v- частота- число колебаний в единицу времени.](https://prezentacii.org/upload/cloud/18/12/82282/images/thumbs/screen18.jpg)
![Если к началу наблюдения фаза имела некоторое начальное значение , то уравнение запишется: гармоническое колебание с начальной фазой. (5). 7. φ- угловая физическая величина, показывающая положение и направление движения колебательной системы в данный момент времени,[рад] 8. φ0- начальная фаза,[рад] Если к началу наблюдения фаза имела некоторое начальное значение , то уравнение запишется: гармоническое колебание с начальной фазой. (5). 7. φ- угловая физическая величина, показывающая положение и направление движения колебательной системы в данный момент времени,[рад] 8. φ0- начальная фаза,[рад]](https://prezentacii.org/upload/cloud/18/12/82282/images/thumbs/screen19.jpg)