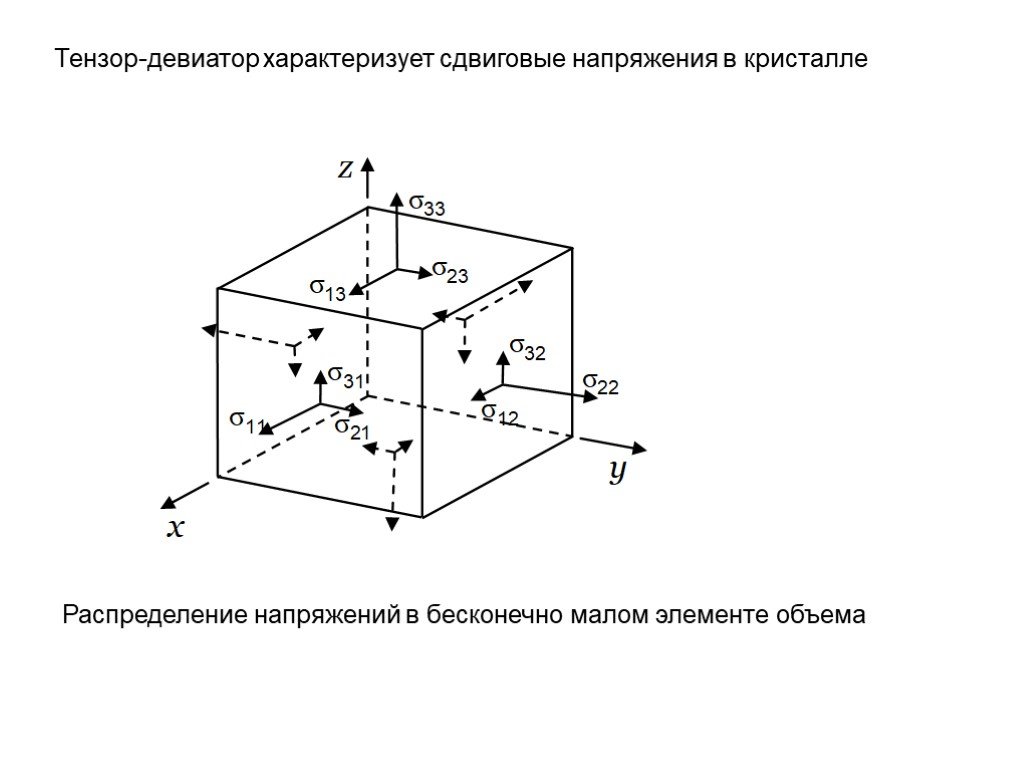
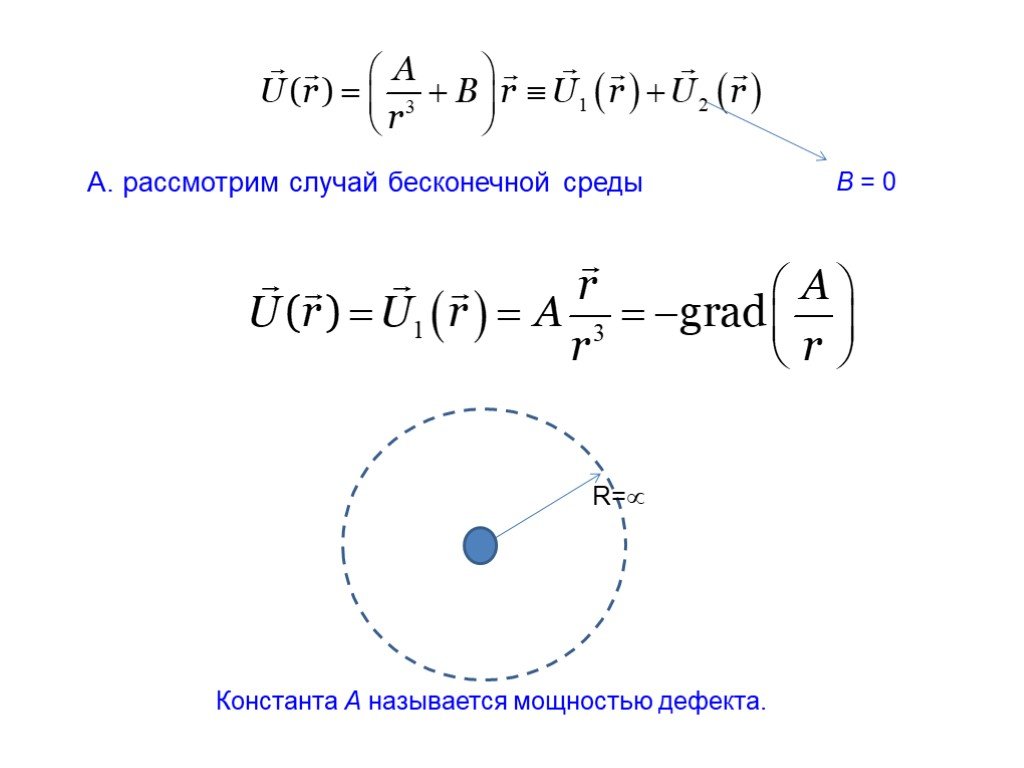
Презентация "Описание дефектов кристаллической структуры в рамках теории упругости" по физике – проект, доклад
Презентацию на тему "Описание дефектов кристаллической структуры в рамках теории упругости" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 23 слайд(ов).
Слайды презентации
Список похожих презентаций
Силы упругости
Цель: Связь между деформацией и силой упругости. Задачи: Объяснить возникновение силы упругости. Рассказать о видах деформации. Сформулировать закон ...Элементы специальной теории относительности
Согласно классическим представлениям о пространстве и времени, считавшимся на протяжении веков незыблемыми, движение не оказывает никакого влияния ...Сила упругости
Сила упругости возникает при деформации тел. Деформация – изменение формы или объема тела. Упругая деформация (исчезает после удаления нагрузки). ...Сила упругости и ее использование
. . . . . . . . . Деформация- это физическое явление, при котором изменяется форма или размеры тела. ВИДЫ ДЕФОРМАЦИЙ ИЗГИБ СДВИГ РАСТЯЖЕНИЕ КРУЧЕНИЕ ...Свойства дефектов и их ансамблей в конденсированных средах
Содержание. Раздел 1 Виды отдельных элементарных дефектов и их свойства. Дефекты в простых веществах 1.1.Классификация дефектов простых веществ 1.1.1.Междоузлие ...Сила упругости
повторение основных понятий, графиков и формул, связанных с силой упругости, а также разбор задач различного уровня сложности в соответствии с кодификатором ...Основные положения молекулярно-кинетической теории
Тема урока. Микропараметры вещества. 1. Молекулярная физика. 1.1. Основы МКТ План урока. 2. Размеры молекул. 3. Число молекул. 4. Масса молекулы. ...Работа силы упругости
Работа силы. Работа А, совершаемая силой F на на конечном участке траектории L точки ее приложения, равна алгебраической сумме работ на всех малых ...Описание механического движения тела
...Книга природы ...написана на языке математики... без неё напрасное блуждание в тёмном лабиринте. Галилео Галилей. Математические линии. y x. . ...Основные положения молекулярно-кинетической теории
МКТ молекулярно-кинетическая теория. объясняет физические явления и свойства тел с точки зрения их внутреннего микроскопического строения. На уроках ...Описание механического движения
ВИДЕОРОЛИКИ. Только просмотр Система отсчета (1) Перемещение (2). МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ. – изменение положения тела в пространстве с течением времени ...Новые преобразования для теории относительности
Цель преобразований:. Введение единых эталонов времени и протяженности для инерциальных систем отсчета (ИСО) S и S', двигающихся друг относительно ...Мини-проект по физике в рамках элективного курса«Как делаются открытия в физике?» Авторы:
Задачи по литературным произведениям. «О, сколько нам открытий чудных готовит просвещенья дух и опыт, сын ошибок трудных, и гений, парадоксов друг ...Элементы теории относительности
Цели урока. Ознакомить учащихся с теорией относительности и её основоположником А. Энштейном. Развивать научное мировоззрение о пространстве и времени. ...Основные положения молекулярно-кинетической теории
Цели урока:. Образовательные: сформулировать основные положения МКТ; раскрыть научное и мировоззренческое значение броуновского движения; установить ...Деятельностный подход в обучении физики в рамках реализации ФГОС общего образования
ГЕРБЕРТ СПЕНСЕР. Великая цель образования – это не знания, а действия. Международные сравнительные исследования. Математическая грамотность. Средний ...Основные положения молекулярно-кинетической теории (МКТ). Абсолютная температура.
Молекулярная физика. Раздел, в котором изучают свойства макроскопических тел в различных агрегатных состояниях на основе МКТ. Демокрит (около 460 ...Развитие теории атомизма
«Выслушай то, что скажу, и ты сам, несомненно, признаешь, Что существуют тела, которых мы видеть не можем……..». КАР ЛУКРЕЦИЙ. ДЕМОКРИТ. Путем размышлений ...Основы молекулярно-кинетической теории
Молекулярно-Кинетическая Теория Представляет собой: Учение, объясняющее тепловые явления в зависимости от внутреннего строения вещества. Молекулярно-кинетической ...Сила тяжести. Вес тела. Сила упругости
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ. 1.Что называется силой тяготения? Где она проявляется ? 2. Сформулировать ЗВТ 3. Каковы пределы применимости ЗВТ? 4. Как называется ...Конспекты
Экспериментальные доказательства молекулярно – кинетической теории
Урок физики в 10 классе. «Экспериментальные доказательства молекулярно – кинетической теории». Подготовила:. Врясова ...Принцип относительности в механике. Постулаты теории относительности
Цуканова Наталья Рефатовна. Преподаватель физики, вторая категория. КГУ «Машиностроительный колледж города Петропавловска». Казахстан ,СКО,г.Петропавловск. ...Сила упругости
Сценарий урока. 7 класс - по учебнику Л.Э.Генденштейн. Тема:. Сила упругости. . Цели урока:. Экспериментально установить причину возникновения ...Основы молекулярно – кинетической теории
Цикл уроков физики в 10 классе. Тема: Основы молекулярно – кинетической теории (5 часов). В процессе работы над модулем вы должны изучить. :. ...Основные положения молекулярно-кинетической теории и ее опытное подтверждение.Масса и размеры молекул
Бегимбаева Жумагуль Купжасаровна. Учитель физики сш №5. Актюбинская область. . Города Шалкар. Тема урока:. "Основные положения ...Основные положения молекулярно-кинетической теории
Обобщающий урок по теме «Основные положения молекулярно-кинетической теории». Цель урока. : обобщение знаний по основным положениям МКТ. Задачи ...Основные положения молекулярно – кинетической теории
Тема: Основные положения молекулярно – кинетической теории. Цель урока. : 1.Учащиеся смогут описывать тепловые явления с помощью статического метода, ...Задачи и вопросы по теории относительности
Задачи и вопросы по теории относительности. В небольшой, но содержательной теме по элементам специальной теории относительности у учителя нет возможностей ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:8 июня 2019
Категория:Физика
Содержит:23 слайд(ов)
Поделись с друзьями:
Скачать презентацию