Презентация "Новые преобразования для теории относительности" по физике – проект, доклад
Презентацию на тему "Новые преобразования для теории относительности" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 18 слайд(ов).
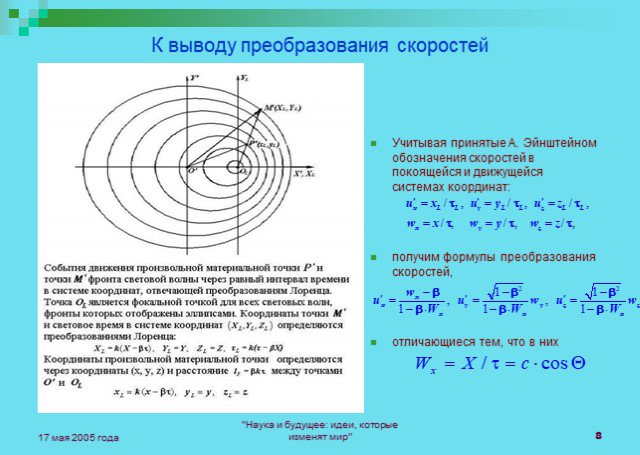
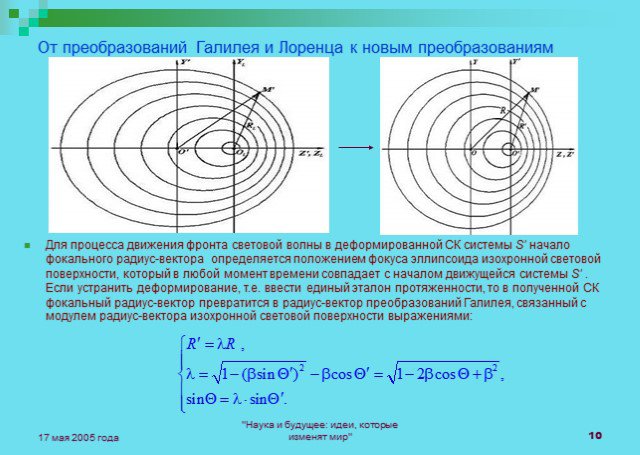
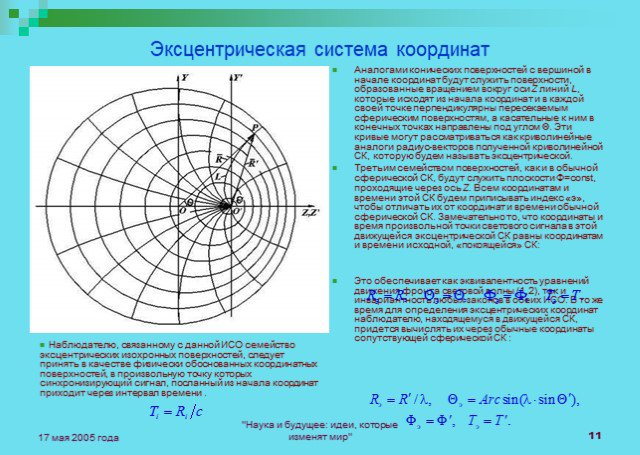
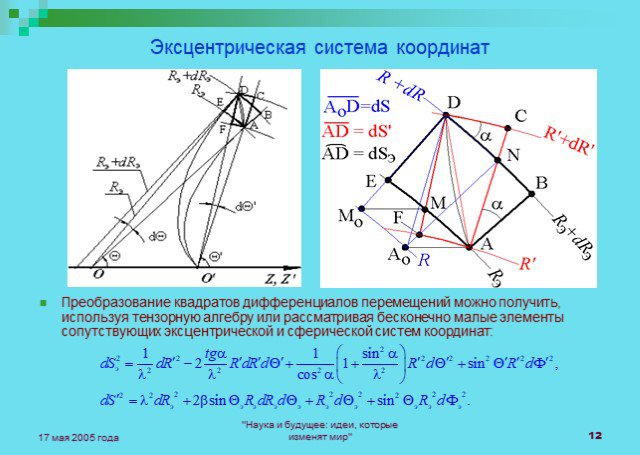
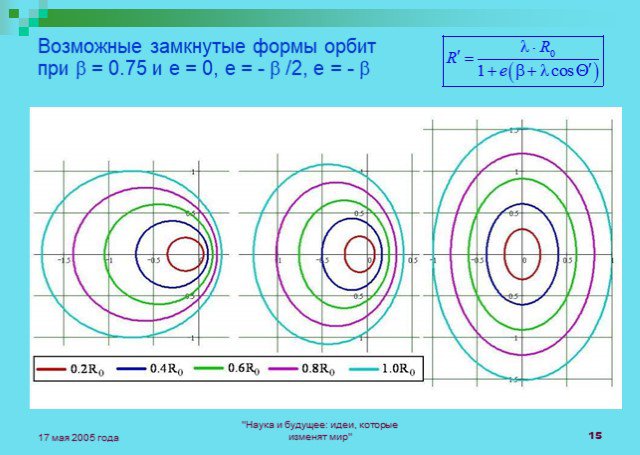
Слайды презентации
Список похожих презентаций
Принципы общей теории относительности
Общая теория относительности (ОТО) — физическая теория пространства-времени и тяготения, основана на экспериментальном принципе эквивалентности гравитационной ...Элементы теории относительности
Содержание. Законы электродинамики и принцип относительности. Постулаты теории относительности и основные следствия, вытекающие из постулатов теории ...Элементы теории относительности
Цели урока. Ознакомить учащихся с теорией относительности и её основоположником А. Энштейном. Развивать научное мировоззрение о пространстве и времени. ...Элементы теории относительности
Принцип относительности в механике и электродинамике. Распространяется ли принцип относительности, справедливый для механических явлений, и на электромагнитные ...Принцип относительности в механике. Постулаты теории относительности
Г. Галилей ввел в классическую механику принцип относительности, смысл которого следующий: законы механики имеют один и тот же вид во всех инерциальных ...Элементы специальной теории относительности
Согласно классическим представлениям о пространстве и времени, считавшимся на протяжении веков незыблемыми, движение не оказывает никакого влияния ...Основы теории относительности
Содержание. Несостоятельность теории Галилея Теории учёных Постулаты теории относительности А.Эйнштейна Релятивистский закон сложения скоростей Относительность ...Постулаты специальной теории относительности
Принцип относительности Галилея. Закон сложения скоростей. При изложении механики предполагалось, что механические явления происходят одинаково в ...Расчёт количества теплоты, необходимого для нагревания тела и выделяемого им при его охлаждении
Цель урока:. определить формулу расчёта количества теплоты, необходимого для изменения температуры тела; проанализировать формулу; отработка практических ...Закон Ома для участка цепи
Вперед за знаниями! Психологический настрой Я нахожусь сейчас на уроке физики. А обо всём остальном я не буду думать сейчас, я подумаю об этом потом. ...Развитие теории атомизма
«Выслушай то, что скажу, и ты сам, несомненно, признаешь, Что существуют тела, которых мы видеть не можем……..». КАР ЛУКРЕЦИЙ. ДЕМОКРИТ. Путем размышлений ...Трудности теории Бора. Квантово-волновой дуализм
Трудности теории Бора. В теории Бора сохранились представления об орбитальном движении электронов в кулоновском поле ядра. Классическая ядерная модель ...Закон Ома для участка цепи
Основные величины, характеризующие электрическую цепь. Характеризует электрическое поле. U вольт [В]. Характеризует сам проводник. Характеризует электрический ...Теория относительности и Альберт Эйнштейн
Альберт Эйнштейн (1879–1955). Кратко об Эйнштейне. Альберт Эйнштейн родился в 1879 году. В 1900 году окончил Цюрихский политехнический институт. В ...Теория относительности Эйнштейна
Краткая аннотация и инструкция по работе с программой. В данной работе рассказывается о теории относительности Эйнштейна, описываются постулаты и ...Общая теория относительности
Тема 9. ОСНОВНЫЕ ПОЛОЖЕНИЯ ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ (ОТО). 9.1. Обобщение закона тяготения Ньютона 9.2. Принцип эквивалентности сил инерции и ...Общая теория относительности Эйнштейна
Физика до теории относительности. Аристотель: движение – переход вещества в форму. Поведение тел определяется соотношением их составе «земли» и «огня». ...Нанотехнологии для всех
Содержание. 1. Введение 2. Развитие нанотехнологий 3. Применение нанотехнологий. 3.1. Медицина 3.2. Промышленность и космонавтика 3.3. Политика. 3.4. ...Нанотехнологии для улучшения комфорта человека
Содержание. Возникновение нанотехнологий. Нанотехнологии Наноматериалы в строительстве Наноматериалы в катализе Наноматериалы в промышленности Наноматериалы ...Модель флюгерного оконного генератора для вырабатывания электрического тока
ВВЕДЕНИЕ. Актуальность исследования. Физические явления, лежащие в основе работы флюгерного оконного генератора. 1. Явление электромагнитной индукции. ...Конспекты
Задачи и вопросы по теории относительности
Задачи и вопросы по теории относительности. В небольшой, но содержательной теме по элементам специальной теории относительности у учителя нет возможностей ...Принцип относительности в механике. Постулаты теории относительности
Цуканова Наталья Рефатовна. Преподаватель физики, вторая категория. КГУ «Машиностроительный колледж города Петропавловска». Казахстан ,СКО,г.Петропавловск. ...Экспериментальные доказательства молекулярно – кинетической теории
Урок физики в 10 классе. «Экспериментальные доказательства молекулярно – кинетической теории». Подготовила:. Врясова ...Физика в примерах и задачах для 9 класса
Рассмотрено на. . заседании методического. объединения учителей физики,. химии и биологии. МАОУ «Гимназия №1». Октябрьского района г. Саратова. ...Третий закон Ньютона. Принцип относительности
План №______. Класс 9. Тема:. Третий закон Ньютона. Принцип относительности. Тип урока:. комбинированный. Цели:. изучить третий закон Ньютона; ...Решение задач на закон Ома для участка цепи
ОТКРЫТЫЙ УРОК по физике. «Решение задач на закон Ома для участка цепи». Учитель: _______ Васильева Зоя Константиновна. Урок по теме. : Решение ...РАЗРАБОТКА УРОКА ПО ФИЗИКЕ С ПРИМЕНЕНИЕМ ТОГИС для 11 класса
1001 идея интересного занятия с детьми. . РАЗРАБОТКА УРОКА ПО ФИЗИКЕ С ПРИМЕНЕНИЕМ ТОГИС. Салионова Галина Георгиевна, преподаватель физики ГБОУ ...Принцип относительности Галилея. Законы Ньютона
Урок физики. Тема:. Принцип относительности Галилея. Законы Ньютона. Цели:. 1. Сформулировать принцип относительности Галилея. Дать знания ...Применение производной для решения задач ЕНТ по физике и математике
Тема урока: «. Применение производной для решения задач ЕНТ по физике и математике». Тип. : интегрированный урок физики и математики. Цели. :. ...Закон Ома для участка цепи
Предмет. физика. . Класс. 10. (Слайд1). Тема урока. : Закон Ома для участка цепи. Цель урока:. . Раскрыть взаимосвязь силы тока, напряжения ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Физика
Автор презентации:В.М. Беляев
Содержит:18 слайд(ов)
Поделись с друзьями:
Скачать презентацию