Конспект урока «Арифметический способ отбора корней» по математике для 11 класса
План - конспект
Тема урока: Арифметический способ отбора корней.
Продолжительность урока: 45 минут.
Место проведения: МКОУ Маломинусинская СОШ №7, 11 класс.
Количество учащихся в классе: 6.
Предмет: математика.
Учитель: Толстихина Ольга Викторовна, 12 разряд.
Цель урока: создать условия для формирования у учащихся умения использовать при решении арифметический способ отбора корней.
Задачи урока:
а) учебно-образовательные:
-
изучить способ арифметического отбора корней, непосредственно подставляя в уравнение и имеющиеся ограничения;
-
закрепить умение учащихся решать тригонометрические уравнения;
-
совершенствовать навыки решения простейших тригонометрических уравнений, вычислительные навыки;
б) учебно-развивающие:
-
развивать внимание, память, мышление, математическую речь;
-
развивать волю и настойчивость, умение преодолевать трудности для решения поставленных задач;
-
развивать умения действовать самостоятельно;
в) учебно-воспитательные:
-
воспитывать добросовестное отношение к учебному процессу;
-
воспитывать положительное отношение к знаниям;
-
воспитывать дисциплинированность;
Методические приемы: частично-поисковый, объяснительно-иллюстративный, практический.
Тип урока: комбинированный – урок изучения нового материала и урок совершенствования знаний, умений, навыков.
Формы работы на уроке: фронтальная, парная, индивидуальная.
Оборудование урока:
-
Техническое обеспечение: демонстрационный экран, мультимедийный проектор.
-
Программное обеспечение: Microsoft Power Point.
-
Плакат.
Литература:
1) А.Г. Корянов, А.А. Прокофьев Материалы курса «Готовим к ЕГЭ хорошистов и отличников»: лекции 1 -4. – М.: Педагогический университет «Первое сентября», 2012. – 104с.
2) Ященко И.В., Шестаков С.А., Трепалин А.С., Захаров П.И. ЕГЭ. Математика. Тематическая рабочая тетрадь. – М.: МЦНМО, Издательство «Экзамен», 2012. – 279, (Серия «ЕГЭ. Тематическая рабочая тетрадь»)
3) Математика. Повышенный уровень ЕГЭ – 2011 (С1, С3). 10-11 классы. Тематические тесты. Уравнения, неравенства, системы/под редакцией Ф.Ф.Лысенко, С.Ю.Кулабухова. – Ростов – на – Дону: Легион – М, 2011. – 128 с. – (Готовимся к ЕГЭ)
План урока:
-
Повторение(10 мин.).
-
Изучение нового материала(8 мин.).
-
Закрепление материала(15 мин).
-
Индивидуальная работа(10 мин.).
-
Подведение итогов урока(2 мин.).
Ход урока:
-
Повторение.
Учитель. Здравствуйте! Садитесь. В прошлом учебном году мы с вами научились решать тригонометрические уравнения. Давайте вспомним, как решаются простейшие тригонометрические уравнения( sin x = a, cos x = a, tg x = a, ctg x = a).
Ученик. sin x = a x = 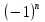 arcsin a + πn, n
arcsin a + πn, n  Z
Z
Учитель. Как ещё можно записать решение этого уравнения?
Ученик. 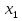 = arcsin a + 2πn, n
= arcsin a + 2πn, n  Z;
Z; 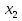 = π - arcsin a + 2πn, n
= π - arcsin a + 2πn, n  Z
Z
Учитель. А как записать частные решения уравнений sin x = -1, sin x = 0,
sin x = 1?
Ученик. sin x = -1, х = - 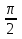 + 2πn, n
+ 2πn, n  Z; sin x = 0, х = πn, n
Z; sin x = 0, х = πn, n  Z; sin x = 1,
Z; sin x = 1,
х = 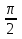 + 2πn, n
+ 2πn, n  Z.
Z.
Учитель. Давайте вспомним решение уравнения cos x = a.
Ученик. соs x = a, x = 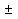 arccos a + 2πn, n
arccos a + 2πn, n  Z;
Z; 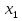 = arccos a + 2πn, n
= arccos a + 2πn, n  Z;
Z; 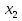 = - arccos a + 2πn, n
= - arccos a + 2πn, n  Z; cos x = -1, х =
Z; cos x = -1, х = 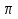 + 2πn, n
+ 2πn, n  Z; cos x = 0, х =
Z; cos x = 0, х = 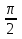 + 2πn, n
+ 2πn, n  Z; cos x = 1, x = 2πn, n
Z; cos x = 1, x = 2πn, n  Z.
Z.
Учитель. Теперь решение уравнений tg x = a и ctg x = a
Ученик. tg x = a, x = arctg a + πn, n  Z;
Z; 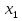 = arctg a + 2πn, n
= arctg a + 2πn, n  Z,
Z, 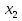 =
= 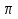 + arctg a + 2πn, n
+ arctg a + 2πn, n  Z; сtg x = a, x = arсctg a + πn, n
Z; сtg x = a, x = arсctg a + πn, n  Z;
Z; 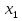 = arcсtg a + 2πn, n
= arcсtg a + 2πn, n  Z,
Z, 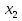 =
= 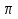 + arсctg a + 2πn, n
+ arсctg a + 2πn, n  Z.
Z.
Учитель. А также повторим формулы приведения (плакат)
2. Изучение нового материала
Учитель. Молодцы! Все ответили правильно. Сегодня мы рассмотрим арифметический способ отбора корней, а именно непосредственную подстановку в уравнение и имеющиеся ограничения. Открываем тетради, записываем дату. Тема урока – Арифметический способ отбора корней (слайд 1).
Рассмотрим примеры (слайд 2). Разберём и запишем в тетради решение данных уравнений. Если по ходу разбора решения будут возникать вопросы, то их можно задавать сразу.
Пример №1 Решить уравнение 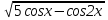 + 2sinx = 0
+ 2sinx = 0
Запишем уравнение в таком виде 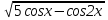 = - 2sinx. Это уравнение равносильно системе
= - 2sinx. Это уравнение равносильно системе 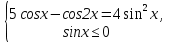 . Решим уравнение:
. Решим уравнение:
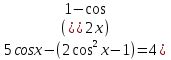
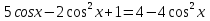
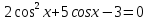
cos x = t
2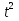 + 5t – 3 = 0
+ 5t – 3 = 0
D = 25- 4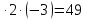
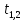 =
= 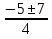 =
= 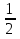 ;-3
;-3
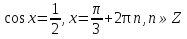 ;
; 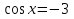 (нет корней)
(нет корней)
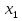 = arccos
= arccos 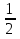 + 2πn, n
+ 2πn, n  Z;
Z; 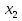 = - arccos
= - arccos 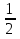 + 2πn, n
+ 2πn, n  Z
Z
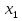 =
= 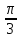 + 2πn, n
+ 2πn, n  Z;
Z; 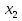 = -
= - 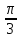 + 2πn, n
+ 2πn, n  Z
Z
sin(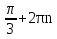 ) = sin
) = sin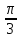 =
= 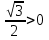 sin(
sin(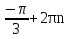 ) = - sin
) = - sin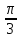 = -
= - 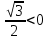
Условие, что 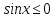 выполняется только для
выполняется только для 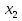 .
.
Ответ: х = - 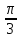 + 2πn, n
+ 2πn, n  Z
Z
Пример №2
Решить уравнение 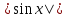 +
+ 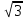 ·cos х = 0
·cos х = 0
Рассмотрим два варианта:
sin x ≥ 0 sin x
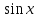 +
+ 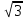 ·cos х = 0
·cos х = 0 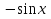 +
+ 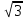 ·cos х = 0
·cos х = 0
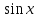 = -
= - 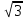 ·cos х
·cos х 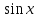 =
= 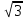 ·cos х
·cos х
tg x = - 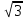 tg x =
tg x = 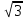
x = - 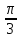 + πk, k
+ πk, k  Z x =
Z x = 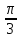 + πk, k
+ πk, k  Z
Z
Отберём х, для которых Отберём х для которых
sin x ≥ 0 sin x
sin(- 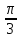 + 2
+ 2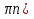 = -
= - 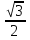 , k = 2n, n
, k = 2n, n Z sin(
Z sin( 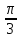 + 2
+ 2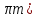 =
= 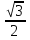 , k = 2m, m
, k = 2m, m Z
Z
sin( 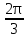 + 2
+ 2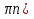 =
= 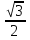 , k = 2n+1, n
, k = 2n+1, n Z sin(
Z sin( 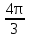 + 2
+ 2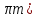 = -
= - 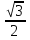 , k = 2m+1, m
, k = 2m+1, m Z
Z
х = 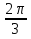 + 2πn, n
+ 2πn, n  Z х =
Z х = 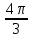 + 2πm, m
+ 2πm, m  Z
Z
Ответ: 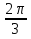 + 2πn,
+ 2πn, 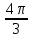 + 2πn, n
+ 2πn, n  Z
Z
Примет №3
Найти корни уравнения sin 3x = 1, удовлетворяющие неравенству cos x 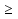 0.
0.
Решим уравнение: sin 3x = 1, х = 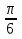 +
+ 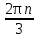 , n
, n  Z
Z
Наименьший положительный период для функций sin 3x и cos x является 2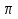 , для проверки неравенства cos(
, для проверки неравенства cos(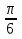 +
+ 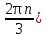 ≥ 0 достаточно рассмотреть значения 0,1,2.
≥ 0 достаточно рассмотреть значения 0,1,2.
cos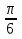 ≥0 и cos
≥0 и cos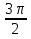 ≥ 0, получаем х =
≥ 0, получаем х = 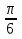 + 2
+ 2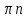 , х =
, х = 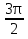 + 2πn, n
+ 2πn, n  Z
Z
Ответ: 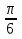 + 2
+ 2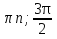 + 2πn, n
+ 2πn, n  Z
Z
3. Закрепление материала
Учитель. Хорошо. Давайте продолжим, и вы попытаетесь выполнить подобные задания в парах. Учитель разбивает класс на и каждой паре дается задание.
1 пара.
Задание. Решить уравнение 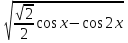 + sin x = 0
+ sin x = 0
Предполагаемый ответ ученика из пары.
системе 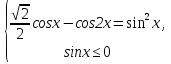 . Решим уравнение:
. Решим уравнение:
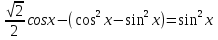
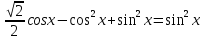
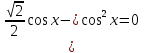
cos x(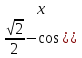 = 0
= 0
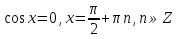 ;
; 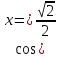
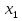 = arccos
= arccos 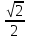 + 2πn, n
+ 2πn, n  Z;
Z; 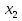 = - arccos
= - arccos 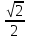 + 2πn, n
+ 2πn, n  Z
Z
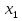 =
= 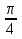 + 2πn, n
+ 2πn, n  Z;
Z; 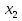 = -
= - 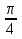 + 2πn, n
+ 2πn, n  Z
Z
sin(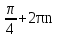 ) = sin
) = sin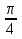 =
= 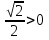 sin(
sin(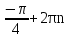 ) = - sin
) = - sin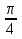 = -
= - 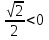
sin(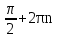 ) = sin
) = sin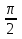 =
= 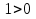
Ответ: - 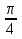 + 2πn, n
+ 2πn, n  Z
Z
Проверим ответ
2 пара.
Задание. Решить уравнение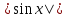 + cos х = 0
+ cos х = 0
Предполагаемый ответ ученика из пары.
Рассмотрим два варианта:
sin x ≥ 0 sin x
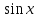 + cos х = 0
+ cos х = 0 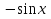 + cos х = 0
+ cos х = 0
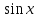 = - cos х
= - cos х 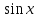 = cos х
= cos х
tg x = - 1 tg x = 1
x = - 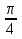 + πk, k
+ πk, k  Z x =
Z x = 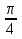 + πk, k
+ πk, k  Z
Z
Отберём х, для которых Отберём х для которых
sin x ≥ 0 sin x
sin(- 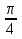 + 2
+ 2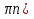 = -
= - 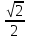 , k = 2n, n
, k = 2n, n Z sin(
Z sin( 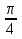 + 2
+ 2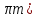 =
= 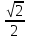 , k = 2m, m
, k = 2m, m Z
Z
sin( 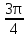 + 2
+ 2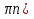 =
= 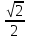 , k = 2n+1, n
, k = 2n+1, n Z sin(
Z sin( 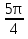 + 2
+ 2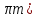 = -
= - 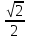 , k = 2m+1, m
, k = 2m+1, m Z
Z
х = 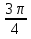 + 2πn, n
+ 2πn, n  Z х =
Z х = 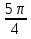 + 2πm, m
+ 2πm, m  Z
Z
Ответ: 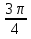 + 2πn;
+ 2πn; 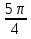 + 2πn, n
+ 2πn, n  Z
Z
Проверим правильный ответ:
3 пара.
Задание. Найдите корни уравнения (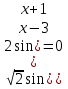 , удовлетворяющие неравенству tg x
, удовлетворяющие неравенству tg x 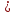 0
0
Предполагаемый ответ ученика из пары.
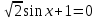
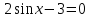
sin x = - 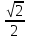 sin x =
sin x = 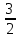 (корней нет)
(корней нет)
x= 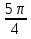 + 2πn, n
+ 2πn, n  Z
Z
x= 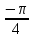 + 2πn, n
+ 2πn, n  Z
Z
tg (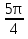 + 2πn) = 1
+ 2πn) = 1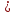 0
0
tg (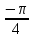 + 2πn) = - 1
+ 2πn) = - 1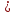 0
0
Ответ: 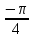 + 2πn, n
+ 2πn, n  Z
Z
Проверим правильный ответ:
4.Индивидуальная работа.
Самостоятельно начать выполнять в тетради задание по карточке.
1) Решите уравнение: 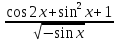 = 0;
= 0;
2) Решите уравнение: 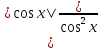 +
+ 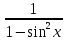 = 2
= 2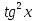 ;
;
3) Найдите все корни уравнения 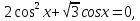
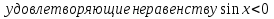
5.Подведение итогов урока.
Учитель. Молодцы! Вы сегодня хорошо потрудились, восстановили в памяти формулы для решения тригонометрических уравнений, познакомились с арифметическим способом отбора корней, применяли его на практике. Что нового и полезного для подготовки к ЕГЭ было сегодня на уроке? На следующих уроках мы продолжим знакомство с этим методом решения тригонометрических уравнений. Домашнее задание: закончить решение заданий по карточке и попытаться найти подобные задания.
Сегодняшний урок мне очень понравился, вы хорошо поработали. Спасибо за урок. Урок закончен. До свидания.
Здесь представлен конспект к уроку на тему «Арифметический способ отбора корней», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (11 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

