Конспект урока «Решение треугольников» по математике

Урок по теме: ”Решение треугольников.”

Урок изучения нового материала.

Цели урока:

1. Повторить определение синуса, косинуса, тангенса, котангенса, теоремы синусов и теоремы косинусов.

2. Научить учащихся решать задачи на использование теоремы синусов и теоремы косинусов.

3. Развивать логическое мышление.

4. Воспитывать внимание.

Ход урока:

1.                  Вступительное слово;

Мы начинаем наш урок по теме: “Решение треугольников”. Необычное для нас сочетание слов. Мы привыкли решать задачи, уравнения, неравенства.

2.                  Повторение.

Для того, чтобы понять новое, надо вспомнить то, что мы уже знаем.

Вспомним соотношения между сторонами и углами прямоугольного треугольника. (ученик комментирует формулы, выведенные на экран)

  Слайд 2

В прямоугольном треугольнике сторона, лежащая против прямого угла, называется гипотенузой, а две другие стороны – катетами.

Известна теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов, т.е.   (см. рисунок). Очень важно уметь находить соотношения между сторонами прямоугольного треугольника.

Синус острого угла равен отношению противолежащего катета к гипотенузе,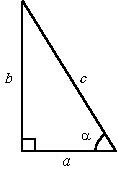

Косинус острого угла равен отношению прилежащего катета к гипотенузе,

Тангенс острого угла равен отношению противолежащего катета к прилежащему катету. 

Котангенс острого угла равен отношению прилежащего катета к противолежащему катету. 

Например, , , ,  согласно имеющемуся рисунку.

3.                  Решите устно:

  Слайд 3

Упражнение

Дано: a,  
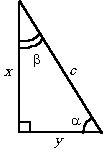
   Найти: x, y.

Ответ: а) x = a tg α, ; б) , x = c sin α, y = c cos α;  

Слайд 3

Теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов.

А

Т

В

С

А

АВ² = ВС² + АС² - 2 ВС АС cos А

Что значит «решить треугольник»?

Перечислим три основные задачи на решение треугольников

а) по двум сторонам и углу между ними

б) по стороне и прилежащим к ней углам

в) по трем сторонам

Слайд 4

Задача: Дан треугольник АВС. Запишите формулу для вычисления:

в

В

д

с

г

А

а

С

б) АВ, если C =Ƴ, b

Ответы:

в) ВС =

д) АС =

г) cos C =

а) B = 180⁰ – (α + γ)

б) АВ =

Слайд 5

Разобрать решение задачи №47 из рабочей тетради (раздать листочки ученикам).

Дать ученикам 2-3 мин на самостоятельное решение, а затем заслушать варианты решений.

Самостоятельно № 26 (1)

Домашнее задание № 26 (2; 4)