Конспект урока «Уравнения – математические модели реальных ситуаций» по математике для 8 класса

План – конспект факультативного занятия по математике

по теме «Уравнения – математические модели реальных ситуаций» (8 класс)

Учитель математики: Жданова М.В.,

МАОУ «Кондратовская СОШ»

Цель: совершенствование навыков составления и выбора математических

моделей при решении текстовых задач.

Задачи:

Обучающие:

1. Актуализировать знания обучающихся: что такое уравнение, корень уравнения, где встречается это понятие, каковы этапы решения текстовых задач с помощью составления математических моделей реальных ситуаций.

2. Организовать работу в парах по алгоритму.

3. Презентовать результаты своей работы.

Развивающие:

1. Развивать математическое мышление и общий кругозор, умение

сравнивать и анализировать, умение обобщать, конкретизировать,

правильно излагать мысли.

2.Развивать самостоятельную деятельность обучающихся.

Воспитывающие:

1.Воспитывать интерес к математике.

2.Воспитывать чувство дружбы, товарищества, умение работать в группе и в паре.

Ход занятия

1. Организационный момент.

2. Актуализация знаний.

Учитель:

Здравствуйте, ребята! Перед вами красивое дерево, часть дерева скрыта от нашего взгляда. Какую часть дерева мы не видим? (Корни)

Где мы встречаемся с понятием «корень»? У чего есть корень? (Корень зуба, корень слова, мои корни - родословная, корни растений,…)

А слово «корень» часто употребляется в русских пословицах, поговорках и в крылатых выражениях.

Знаете ли вы такие пословицы?

Продолжите крылатое выражение «Зри… в корень!»

В чем заключается смысл этого выражения? (Вникай в самую суть дела)

А в математике где мы встречаемся с корнями? (Корни уравнений, квадратные корни, арифметические квадратные корни)

Что такое уравнение? (Равенство, содержащее переменную)

Что называют корнем уравнения? (Значение переменной, которое обращает уравнение в верное числовое равенство)

Уравнения – это математические модели реальных ситуаций.

Я предлагаю вам две реальные ситуации. Попробуйте выбрать ту математическую модель, которая описывает данную реальную ситуацию?

№1. Бамбук – самое быстрорастущее растение. Его средняя скорость роста составляет 2,5 см в час. Найдите зависимость роста h (см) от времени t (ч) роста. Укажите номер математической модели.

1) 2,5h = t ; 2) t : h = 2,5; 3) h = 2,5 t. (Ответ 3).

Сколько переменных в уравнении? (Две)

Какая эта зависимость? (Функциональная, прямая пропорциональность)

№2. В классе девочек вдвое больше, чем мальчиков. Если из этого класса уйдут три девочки и придут три мальчика, то девочек будет на 4 больше, чем мальчиков. Сколько мальчиков в классе?

Пусть в классе х мальчиков…

1) (х+3) – (2х-3) = 4; 2) (2х-3) – (х+3) = 4; 3) (2х-3) = 4 - (х+3). (Ответ 2)

3. Постановка темы и цели урока.

Попробуйте определить тему нашего занятия?

Уравнения – математические модели реальных ситуаций.

Как вы думаете, а какие цели нашего занятия?

Совершенствование навыков составления и выбора математических моделей при решении текстовых задач.

А сейчас я предлагаю вам определить последовательность этапов решения текстовых задач. На ваших столах есть карточки, где вам нужно маркером поставить номер этапа. (Этап №1. Составление математической модели. Этап №2. Работа с математической моделью. Этап №3. Ответ на вопрос задачи)

Какой из данных этапов самый главный? (Первый)

Почему? (Это доказывают критерии оценки текстовых задач во второй части экзаменационной работы на ЕГЭ и на ОГЭ; ….)

4.Работа в парах.

Что необходимо иметь для работы в паре? Давайте проверим, все ли у нас есть: алгоритм работы (приложение), карточки с заданиями, черновики, дополнительные материалы, маркеры для оформления результата вашей работы (приложение), ручки. Во время работы, договоритесь между собой, как вы будете презентовать свой результат. Время работы в паре 7 минут. Презентация работы 1,5 минуты. Хранитель времени – песочные часы.

5. Презентация парной работы.

Пары презентуют свою работу.

Учитель:

Ребята, вы молодцы! Вы справились с выбором математической модели в задании №1 и верно соотнесли с реальной ситуацией. А задание №2 действительно было сложным т. к. это задание из второй части экзаменационной работы за 9 класс, с такими уравнениями у вас еще нет навыков работы, я желаю вам их так же хорошо научиться решать.

Как вы считаете, достигли ли мы поставленной цели?

Да, действительно, поставленную цель мы достигли. Не даром говориться: «Корень учения горек да плод сладок!»

6. Рефлексия.

Художники рисуют красками, нарисуем свое понимание темы нашего занятия цветом яблок.

Если вы поняли материал, то выбирайте яблоко красное.

А если у вас остались вопросы, то ваши яблоки желтые.

Выбираем яблоко, соответствующего цвета и идем к дереву знаний.

Ребята, посмотрите, какое дерево у нас получилось! Каков корень таков и плод!

А я дарю вам яблоки зеленые, плоды – символ знания и желаю вам во всем доходить до самой сути! Спасибо за работу!

Приложение.

1. Алгоритм работы в паре

1) Решить задачи на черновике и совместно обсудить

(при выполнении задания №2 можно воспользоваться дополнительными материалами, которые находятся на рабочем столе нетбука, в папке «Занятие»)

2) Оформить результат работы

3) Презентовать работу у доски за 1,5 минуты

(что получилось, какие проблемы возникли при выполнении заданий и почему; приготовить 1 вопрос к тем, кто презентует свою работу)

2. Результат работы

Пара №1

№

ФИО
1
2

Задание №1

Установите соответствие между реальной ситуацией и ее математической моделью.

Результат работы занесите в бланк ответа.

Реальная ситуация

Математическая модель
Пусть х – число девочек, у – число мальчиков.
А: Девочек в два раза больше, чем мальчиков.	1.
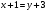
Б: Если в класс придут еще одна девочка и три мальчика, то девочек и мальчиков станет поровну.	2.
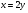
В: Если из класса уйдут три девочки, то мальчиков станет в три раза больше.	3.

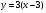
БЛАНК ОТВЕТА К ЗАДАНИЮ №1

А

Б	В

Задание №2

Реальная ситуация

Математическая модель
Скорость первого велосипедиста на 5 км/ч больше, чем скорость второго, поэтому он преодолевает маршрут длиной 10 км на 6 мин быстрее, чем второй велосипедист. За какое время первый велосипедист проходит этот маршрут? Составьте математическую модель данной реальной ситуации.

Пара №2

№

ФИО
1
2

Задание №1

Установите соответствие между реальной ситуацией и ее математической моделью. Результат работы занесите в бланк ответа.

Реальная ситуация

Математическая модель
Пусть х – количество книг на первой полке, у – количество книг на второй полке.
А: На первой полке в два раза больше книг, чем на второй полке.	1.
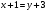
Б: Если на первую полку добавить одну книгу, а на вторую – три книги, то книг на полках станет поровну.	2.
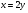
В: Если с первой полки снять три книги, то на второй полке книг станет в три раза больше.	3.

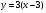
БЛАНК ОТВЕТА К ЗАДАНИЮ №1

А

Б	В

Задание №2

Реальная ситуация

Математическая модель
Водитель автомобиля вынужден был по дороге сделать остановку, затратив на это 12 мин. Чтобы прибыть в конечный пункт вовремя, он увеличил скорость на 10 км/ч и ликвидировал опоздание на перегоне в 60 км. С какой скоростью двигался автомобиль на этом перегоне? Составьте математическую модель данной реальной ситуации.

Пара №3

№

ФИО
1
2

Задание №1

Установите соответствие между реальной ситуацией и ее математической моделью.

Результат работы занесите в бланк ответа.

Реальная ситуация

Математическая модель
Пусть х –количество роз в одном букете, у –количество роз в другом букете.
А: В одном букете в два раза больше роз, чем в другом.	1.
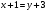
Б: Если в первый букет добавить одну розу, а во второй букет – три розы, то роз в букетах станет поровну.	2.
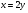
В: Если из одного букета убрать три розы, то в другом букете роз станет в три раза больше.	3.

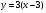
БЛАНК ОТВЕТА К ЗАДАНИЮ №1

А

Б	В

Задание №2

Реальная ситуация

Математическая модель
Скорость лодки на 5 км/ч меньше, чем скорость катера, поэтому он проходит маршрут 10 км на 6 мин медленнее, чем катер. За какое время катер проходит этот маршрут? Составьте математическую модель данной реальной ситуации.

Пара №4

№

ФИО
1
2

Задание №1

Установите соответствие между реальной ситуацией и ее математической моделью.

Результат работы занесите в бланк ответа.

Реальная ситуация

Математическая модель
Пусть х – количество яблок в ящике, у – количество яблок в корзине.
А: В ящике в два раза больше яблок, чем в корзине.	1.
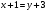
Б: Если в ящик добавить одно яблоко, а в корзину добавить три яблока, то яблок в ящике и в корзине станет поровну.	2.
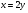
В: Если из ящика убрать три яблока, то в корзине яблок станет в три раза больше.	3.

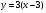
БЛАНК ОТВЕТА К ЗАДАНИЮ №1

А

Б	В

Задание №2

Реальная ситуация

Математическая модель
Водитель автомобиля вынужден был по дороге сделать остановку, затратив на это 12 мин. Чтобы прибыть в конечный пункт вовремя, он увеличил скорость на 10 км/ч и ликвидировал опоздание на перегоне в 60 км. С какой скоростью двигался автомобиль на этом перегоне? Составьте математическую модель данной реальной ситуации.