Презентация "Свойства параллельных прямых" по математике – проект, доклад
Презентацию на тему "Свойства параллельных прямых" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 17 слайд(ов).
Слайды презентации
Список похожих презентаций
Свойства параллельных прямых
Цели урока:. Рассмотреть свойства параллельных прямых. Показать учащимся применение свойств параллельных прямых. Закрепить знания, умения и навыки ...Признаки параллельности прямых. Свойства параллельных прямых
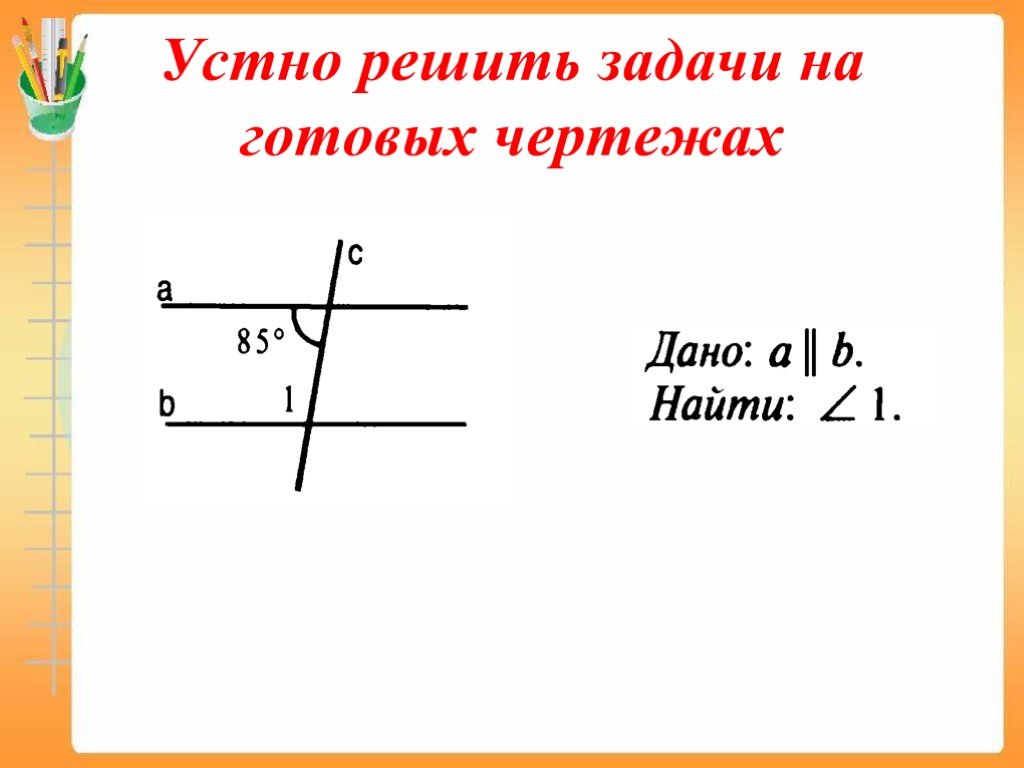
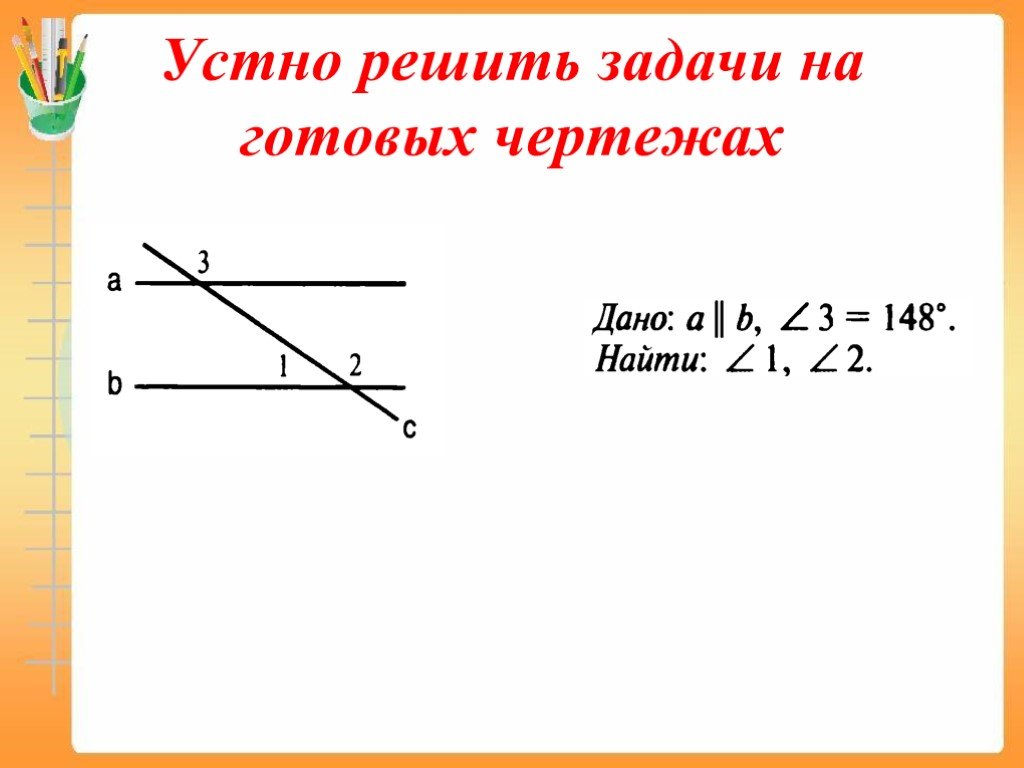
. УСТАНОВИТЕ СООТВЕТСТВИЕ:. 2 и 3 накрест лежащие 7 и 4 5 и 7 соответственные 5 и 4 3 и 4 односторонние 4 и 8 1 и 4 вертикальные 1 и 3 7 и 3 смежные ...Признаки и свойства параллельных прямых
Игра «Я знаю все!». - Параллельными называются прямые……... - Два отрезка называются параллельными, если…. - Если прямая пересекает одну из параллельных ...Аксиома параллельных прямых
Аксиомами называются те основные положения геометрии, которые принимаются в качестве исходных положений, на основе которых доказываются далее теоремы ...Построение перпендикулярных и параллельных прямых
Цели урока:. - способствовать выработке навыков и умений в построении параллельных и перпендикулярных прямых; - развивать навыки и умения при решении ...Аксиома параллельных прямых
Теорема Теорема Теорема Теорема. Об аксиомах геометрии. А на чём основаны доказательства самых первых теорем геометрии? На аксиомах. Утверждениях ...Определение параллельных прямых
. . . Составьте конспект п. 24. Вопрос Какие прямые называются параллельными? Изобразите и обозначьте параллельные прямые Какие отрезки называются ...Аксиома параллельных прямых
Аксио́ма – исходное утверждение, принимаемое истинным без доказательств, и которое в последующем служит «фундаментом» для построения какой-либо теории, ...Вводное повторение курса геометрии о параллельных прямых
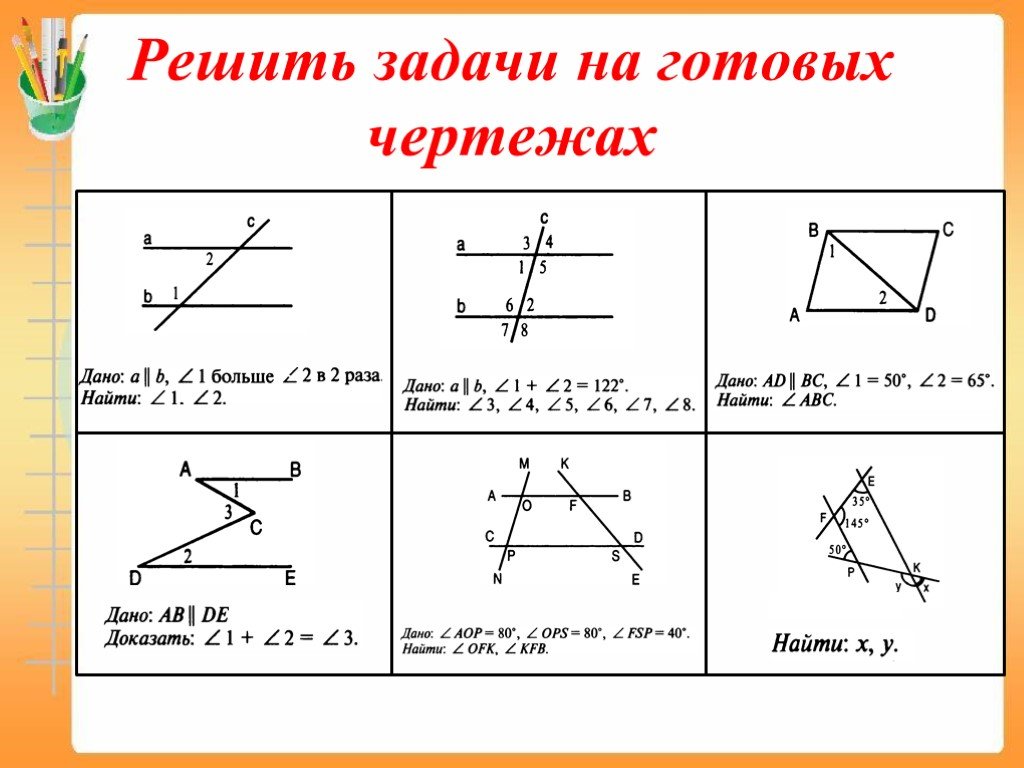
Назвать все углы, образовавшиеся при пересечении двух прямых третьей. 1 3 4 5 6 7 8 а в. Задача №1 2 А В Е К. Дано:. Задача № 2 С. Отрезки АВ и СЕ ...Геометрия «Аксиома параллельных прямых»
«Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение». (В. Произволов). ...Определение параллельных прямых
ЦЕЛИ УРОКА:. Ввести понятие параллельных прямых; Секущей прямой; Накрест лежащих углов; Односторонних углов; Соответственных углов; Научится определять ...Свойства медиан в прямоугольном треугольнике
Из ΔАВС (С=900) АВ2=ВС2+АС2 АВ2=5 Из Δ ДВА(А=900) Х2=АВ2+АD2 X2=6. ИзΔАВС(С=900) АС2=АВ2-ВС2 АС2=12 Из ΔАDC (C=900) X2=AC2+CD2 X2=13. Из ΔАВС ...Свойства и графики элементарных функций
1. Определение функции. 2. Линейная функция: возрастающая; убывающая; частные случаи. 3. Квадратичная функция. 4. Степенная функция: с четным натуральным ...Взаимное расположение двух прямых
Пересекающиеся прямые. Графический признак: (a ∩ b = K) (ai ∩ bi = Ki), (aj ∩ bj = Kj), Ki Kj xi,j, т.е. если две прямые a и b пересекаются в ...Свойства степени с натуральным показателем
Задачи урока: - повторить и закрепить изученный материал о степени с натуральным показателем через игровые формы работы; - активизировать мыслительную ...Свойства сложения и умножения
Свойства сложения. Переместительный закон сложения. 2 + 3 = 5 3 + 2 = 5 2+3 = 3+2 a+b = b+a. Переместительный закон сложения:. a+b = b+a При перестановке ...Свойства равнобедренного треугольника
Теоретический опрос. Объясните, какой отрезок называется перпендикуляром, проведённым из данной точки к данной прямой. Сформулируйте и докажите теорему ...Логарифмы. Свойства логарифмов
Изобретатель первых логарифмических таблиц, впервые ввёл сам термин «логарифм» шотландский математик Джон Непер. «Я старался, насколько мог и умел, ...Логарифмы. Свойства логарифма
ЛОГАРИФМЫ. Во многих задачах требуется уметь решать уравнения вида a =b. Для этого надо найти показатель степени по данным значениям степени и её ...Взаимное расположение прямых, заданных уравнениями вида у=кх+в
Цели:. Выяснить зависимость расположения графиков прямых от значений k и b. Формирование умений и навыков по внешнему виду определять взаимное расположение ...Конспекты
Свойства параллельных прямых
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа с. Урицкое Лысогорского района Саратовской области». ...Признаки и свойства параллельных прямых
Муниципальное образовательное учреждение. «Средняя общеобразовательная школа №7». города Твери. Конспект урока по геометрии в 7 классе«Признаки ...Аксиома параллельных прямых
Кондручина Надежда Сергеевна,. . учитель математики МКОУ «Панкрушихинская сош»,. . Панкрушихинский район Алтайского края. Предмет:. Геометрия. ...Аксиома параллельных прямых
Открытый урок геометрии в 7 классе. Тема урока: «Аксиома параллельных прямых». Дата проведения урока: 16 января 2014 года. Учитель: Олейникова ...Признаки параллельных прямых
Муниципальное общеобразовательное учреждение. . Спас-Заулковская школа-интернат среднего (полного) общего образования –. . Центр образования ...Свойства степени с натуральным показателем
Автор –. Громенюк Анна Вячеславовна. Предмет. – алгебра 7 класс (урок алгебры). Учебно-методическое обеспечение:. учебник алгебры, 7 класс [1]. ...Свойства степеней в преобразовании выражений
Муниципальное общеобразовательное учреждение Борисоглебская средняя общеобразовательная школа № 4. « Свойства степеней в. преобразовании ...Свойства сложения
Открытый урок «Свойства сложения» 2 класс. . Этапы урока. . . Деятельность учителя. . Деятельность учеников. . . 1-й этап: Организационный ...Свойства сложения
Математика. . . Тема урока: «Свойства сложения». . Цели урока: закрепление переместительного и сочетательного свойств сложения;преобразование ...Трапеция. Свойства трапеции
МБОУ гимназия № 12. . Ахонен Екатерина Петровна. . Геометрия. . 8 класс. . . Профильный уровень, используемые учебники: Геометрия: ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:12 октября 2018
Категория:Математика
Содержит:17 слайд(ов)
Поделись с друзьями:
Скачать презентацию