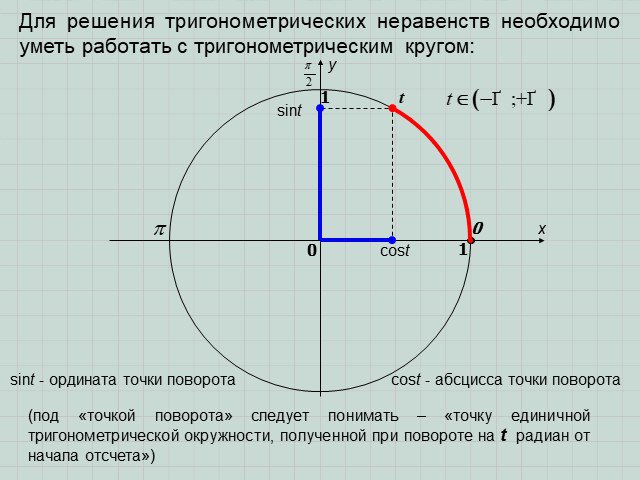
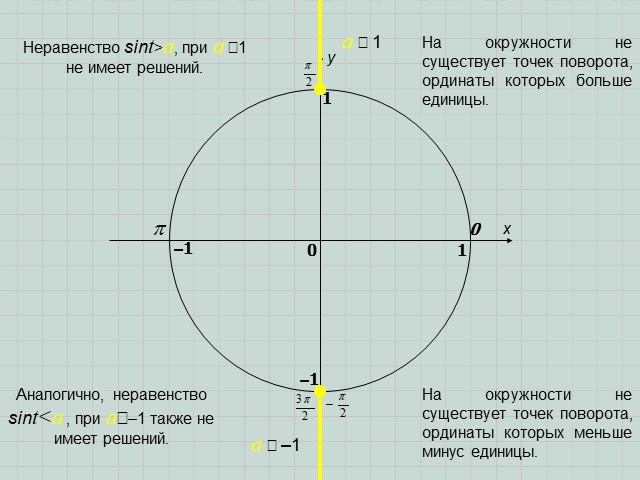
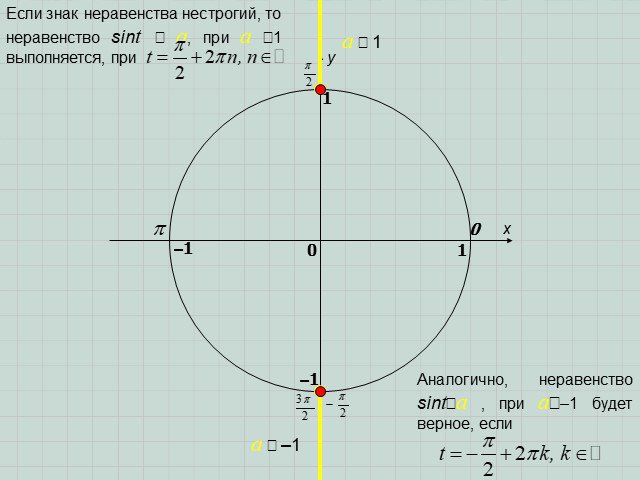
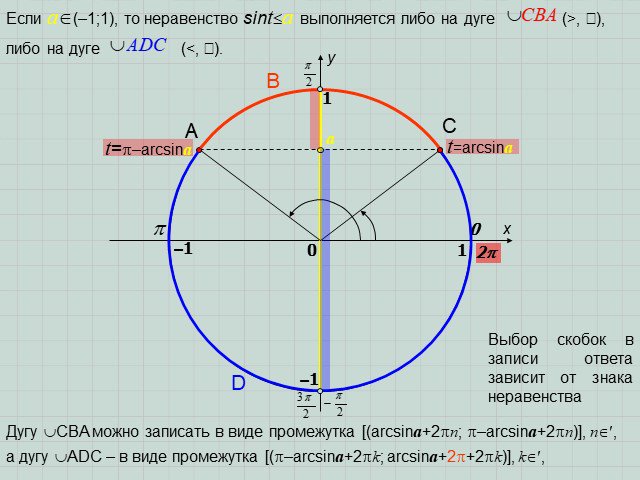
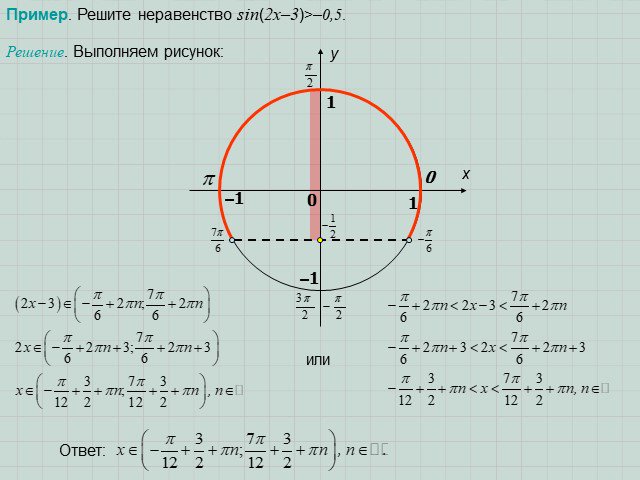
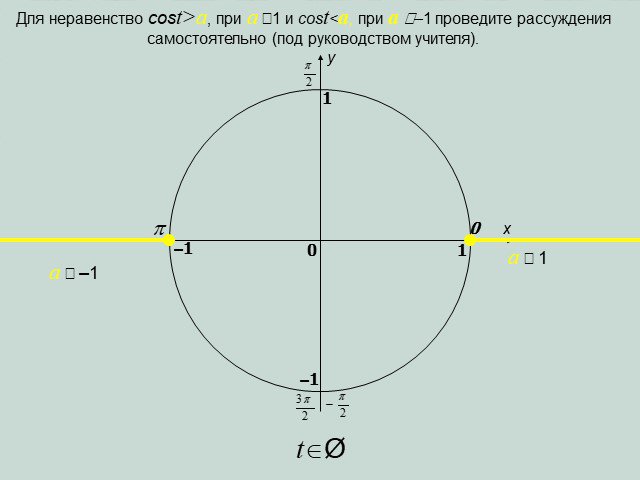
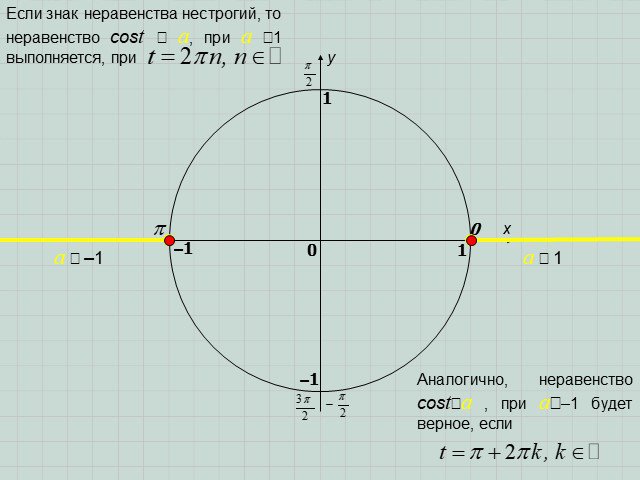
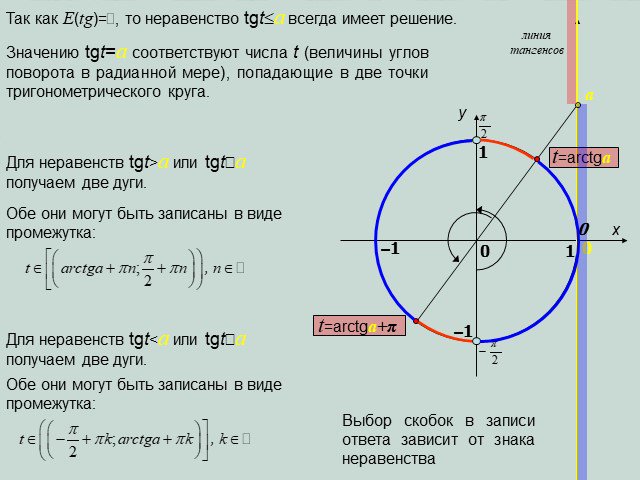
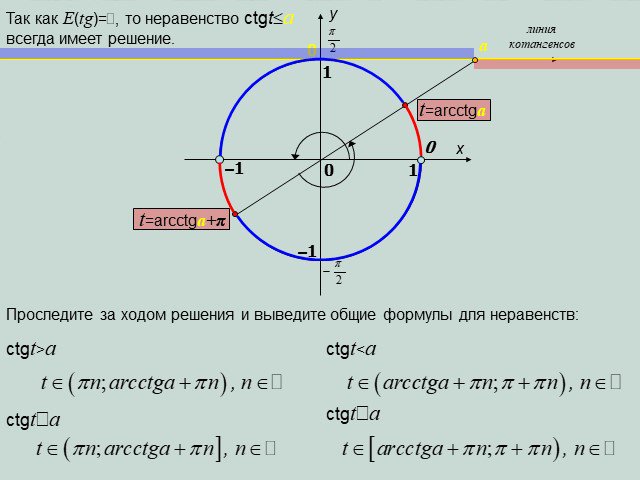
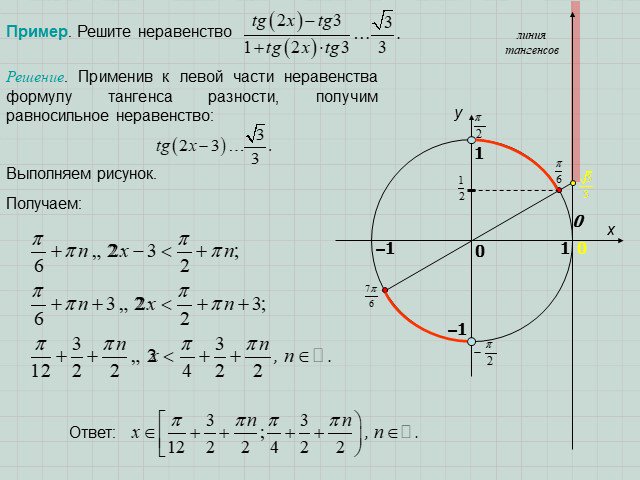
Презентация "Решение простейших тригонометрических неравенств" по математике – проект, доклад

Воробьев Леонид Альбертович, г.Минск

Алгебра и начала анализа, 10 класс.

Решение простейших тригонометрических неравенств.

Под простейшими тригонометрическими неравенствами понимают неравенства вида:

,где t – выражение с переменной, a.

Под знаком “” следует понимать любой из четырёх знаков неравенств: <, >, , .

Для решения тригонометрических неравенств необходимо уметь работать с тригонометрическим кругом:

sint cost t x y 0 1

sint - ордината точки поворота

cost - абсцисса точки поворота

(под «точкой поворота» следует понимать – «точку единичной тригонометрической окружности, полученной при повороте на t радиан от начала отсчета»)

–1 a  1 a  –1

Аналогично, неравенство sint

Неравенство sint>a, при a 1 не имеет решений.

На окружности не существует точек поворота, ординаты которых больше единицы.

На окружности не существует точек поворота, ординаты которых меньше минус единицы.

Если знак неравенства нестрогий, то неравенство sint  a, при a 1 выполняется, при

Аналогично, неравенство sinta , при a–1 будет верное, если

t=arcsina t=–arcsina a 2

Если a(–1;1), то неравенство sinta выполняется либо на дуге (>, ),

A D B C либо на дуге (<, ).

Выбор скобок в записи ответа зависит от знака неравенства

Дугу CBA можно записать в виде промежутка [(arcsina+2n; –arcsina+2n)], n,

а дугу ADC – в виде промежутка [(–arcsina+2k; arcsina+2+2k)], k,

Пример. Решите неравенство sin(2x–3)>–0,5.

Решение. Выполняем рисунок:

или Ответ:

Для неравенство cost>a, при a 1 и cost

tØ

Если знак неравенства нестрогий, то неравенство cost  a, при a 1 выполняется, при

Аналогично, неравенство costa , при a–1 будет верное, если

Если a(–1;1), то неравенство costa выполняется либо на дуге (>, ),

В первом случае Во втором, t=arccosa t=–arccosa

Пример. Решите неравенство .

линия тангенсов

Так как E(tg)=, то неравенство tgta всегда имеет решение.

Значению tgt=a соответствуют числа t (величины углов поворота в радианной мере), попадающие в две точки тригонометрического круга.

Для неравенств tgt>a или tgta получаем две дуги.

Обе они могут быть записаны в виде промежутка:

Для неравенств tgt

линия котангенсов

Проследите за ходом решения и выведите общие формулы для неравенств:

Так как E(tg)=, то неравенство сtgta всегда имеет решение.

ctgt>a ctgta ctgt

Пример. Решите неравенство

Решение. Применив к левой части неравенства формулу тангенса разности, получим равносильное неравенство: Выполняем рисунок.

Получаем: