Презентация "Неравенства" по математике – проект, доклад
Презентацию на тему "Неравенства" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 30 слайд(ов).
Слайды презентации
Список похожих презентаций
Неравенства с одной переменной и их свойства
1.Числовые промежутки. х>6, х. 5) -3. Множество действительных чисел изображается всей координатной прямой. Его обозначают так: (-∞;∞). Например: ...Неравенства с двумя переменными
познакомиться с определением неравенства с двумя переменными и понятием решения неравенства с двумя переменными; познакомиться со способом решения ...Неравенства с одной переменной
Решите устно 1. Сколько целых чисел входит в промежуток (-2; 4] ? Б. 7 В. 5 Г. 4 2. Корнями уравнения х²-4х-21=0 являются числа: А. -7и3 Б. 7и3 Г. ...Неравенства и их системы
1). Определение 2). Виды 3). Свойства числовых неравенств 4). Основные свойства неравенств 4). Типы 5). Способы решения. Запись вида а>в или а. Неравенства ...Неравенства с двумя переменными
№ 484а. № 484г. № 486 а. № 486 б. № 486 в. № 486 г. № 487 б. № 487 г. № 488 а. № 492 а. ...Неравенства и их решения
Неравенство Решить неравенство. Совокупность неравенств. Неравенства Алгебраические Трансцендентные рациональные иррациональные. Пример: Решить неравенство ...Неравенства в математике
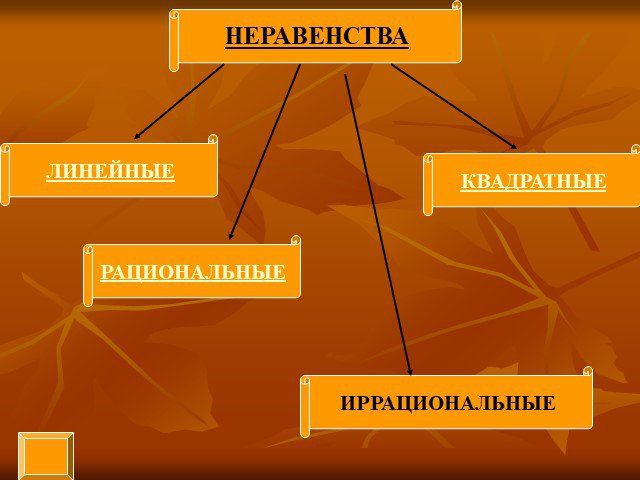
Разработано учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми Мишариной Альбиной Геннадьевной. СОДЕРЖАНИЕ. Линейные неравенства ...Неравенства
Решить неравенства:. 3х+6>0 8-x>0 4( x+5) 0 0·x >0 0·x< 0. Сравните с нулем:. Х- неотрицательное число Х- положительное число Х- отрицательное число. ...График квадратичной функции. Неравенства с одной переменной
Квадратичная функция и ее график. Квадратичной функцией называется функция, которую можно задать формулой вида y = ax² + bx + c, где х – независимая ...График квадратичной функции Неравенства с одной переменной
Квадратичная функция и ее график. Квадратичной функцией называется функция, которую можно задать формулой вида y = ax² + bx + c, где х – независимая ...Конспекты
Равенства. Неравенства
Урок математики в 1 классе. Тема: Равенства. Неравенства. Цель:. знакомство с терминами « равенство», « неравенство». Задачи:. . . формировать ...Неравенства с одной переменной
. . Школьный фестиваль педагогического творчества. «Открытый урок – маленький шедевр». МБОУ СОШ п. Рощинский. Неравенства с одной ...Неравенства с модулем
Алгебра. 9 класс. Тема: Неравенства с модулем. . Цель. :. формировать умения решать неравенства с модулем вида │f. (x. ) │a и │ f. (x. ) │> ...Неравенства и уравнения, содержащие степень
Неравенства и уравнения, содержащие степень. Цель:. провести систематизацию и обобщение знаний по вопросам решения уравнений и неравенств; рассмотреть ...Неравенства
УРОК ПО ТЕМЕ:. НЕРАВЕНСТВА. (ОБОБЩАЮЩИЙ УРОК). УЧИТЕЛЬ. МОУ СОШ№7. . Бородина Ольга Борисовна. г. ...Неравенства
Негосударственное образовательное учреждение. «Средняя общеобразовательная школа с углубленным изучением. отдельных предметов имени В.Д.Чурсина ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 января 2015
Категория:Математика
Содержит:30 слайд(ов)
Поделись с друзьями:
Скачать презентацию












































![Пример: х²+5х-6≤0 y= х²+5х-6 (квадратичная функция, график парабола, а=1, ветви направлены вверх) х²+5х-6=0; корни этого уравнения: 1 и -6. у + + -6 1 x Ответ: [-6;1]. - Пример: х²+5х-6≤0 y= х²+5х-6 (квадратичная функция, график парабола, а=1, ветви направлены вверх) х²+5х-6=0; корни этого уравнения: 1 и -6. у + + -6 1 x Ответ: [-6;1]. -](https://prezentacii.org/upload/cloud/15/01/19211/images/thumbs/screen18.jpg)
![Решите графически неравенства: 1).х²-3х0; 3).х²+2х≥0; 4). -2х²+х+1≤0; (0;3) (-∞;0)U(4;+∞) (-∞;-2]U[0;+∞) (-∞;-0,5]U[1;+∞) Решите графически неравенства: 1).х²-3х0; 3).х²+2х≥0; 4). -2х²+х+1≤0; (0;3) (-∞;0)U(4;+∞) (-∞;-2]U[0;+∞) (-∞;-0,5]U[1;+∞)](https://prezentacii.org/upload/cloud/15/01/19211/images/thumbs/screen19.jpg)































