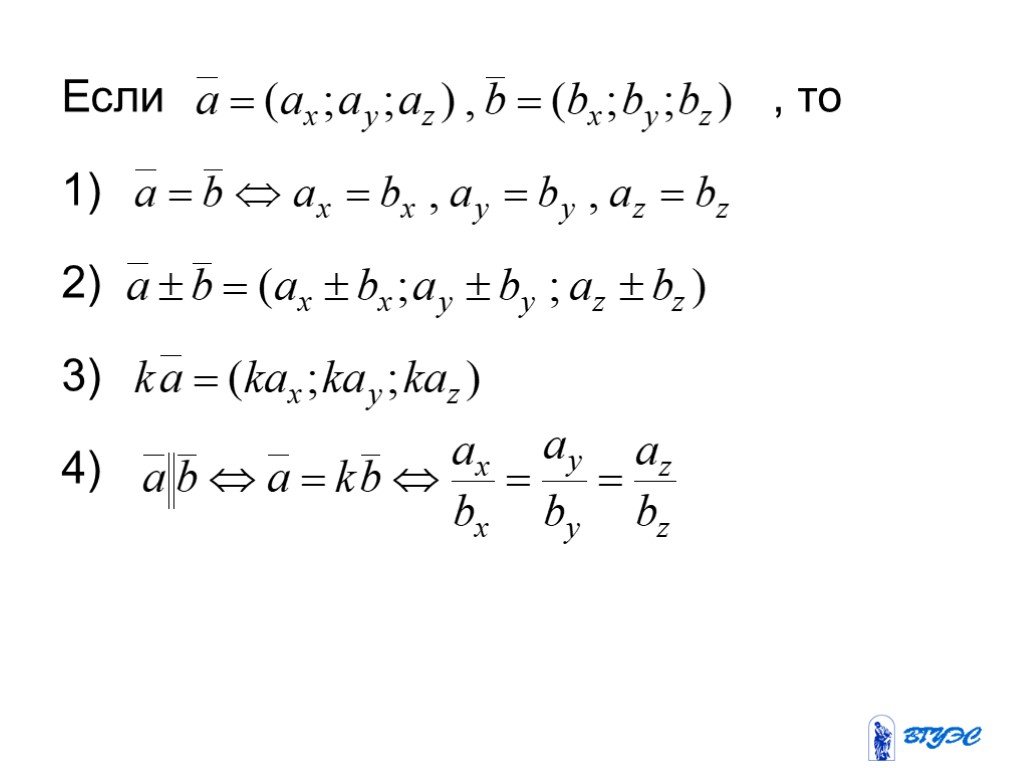Презентация "Математика" – проект, доклад

ВГУЭС

Кафедра математики и моделирования

МАТЕМАТИКА для специальности 030301.65 «Психология»

Преподаватель Пивоварова Ирина Викторовна

Содержание курса

Определители Матрицы Системы линейных алгебраических уравнений Векторная алгебра Прямая на плоскости Теория вероятностей. Случайные события Случайные величины

Тема 1. Определители

Определение. Определителем 2-го порядка называется выражение Числа – элементы определителя, элементы называют элементами главной диагонали определителя.

Определение. Определителем 3-го порядка называется выражение

Определение. Минором элемента определителя 3-го порядка называется определитель 2-го порядка, получающийся из данного определителя вычеркиванием строки и столбца, на пересечении которых стоит данный элемент. Обозначение:

Определение. Алгебраическим дополнением элемента определителя 3-го порядка называется его минор, взятый со знаком плюс, если сумма индексов i + j четная, и со знаком минус, если сумма индексов i + j нечетная. Обозначение:

Теорема разложения. Определитель 3-го порядка равен сумме произведений элементов какого-либо ряда определителя на их алгебраические дополнения (под рядом понимается строка или столбец).

Имеют место шесть разложений:

Свойства определителей Определитель не меняет своего значения при замене всех его строк соответствующими столбцами. При перестановке двух параллельных рядов определитель меняет значение на противоположное. Определитель с двумя одинаковыми рядами равен нулю.

Свойства определителей (продолжение) Если все элементы какого-либо ряда равны нулю, то определитель равен нулю. Общий множитель элементов какого-либо ряда определителя можно выносить за знак определителя.

Свойства определителей (продолжение) Величина определителя не изменится, если к элементам какого-либо ряда определителя прибавить элементы параллельного ряда, умноженные на одно и то же число.

Ключевые понятия

Определитель, порядок определителя, минор, алгебраическое дополнение, главная диагональ определителя.

Вопросы для самопроверки по теме «Определители»

Определение определителя 2-го, 3-го порядка. Минор, алгебраическое дополнение элемента. Теорема разложения. Свойства определителей.

Тема 2. Матрицы

Определение. Матрицей размеров mn называется совокупность m·n чисел, расположенных в виде таблицы из m строк и n столбцов. Краткое обозначение:

Определение. Матрица размера mm называется квадратной. Определение. Две матрицы считаются равными, если равны их размеры и равны элементы, стоящие на одинаковых местах.

Определение. Суммой матриц называется матрица , каждый элемент которой равен сумме соответствующих элементов матриц A и B, то есть

Определение. Произведением матрицы на число  называется матрица , каждый элемент которой равен

Определение. Произведением матрицы на матрицу называется матрица , каждый элемент которой равен сумме произведений элементов i-ой строки матрицы A и соответствующих элементов j-го столбца матрицы B:

Так как в произведении матриц строки и столбцы не равноправны, то . Определение. Матрица, все элементы которой равны нулю, называется нулевой.

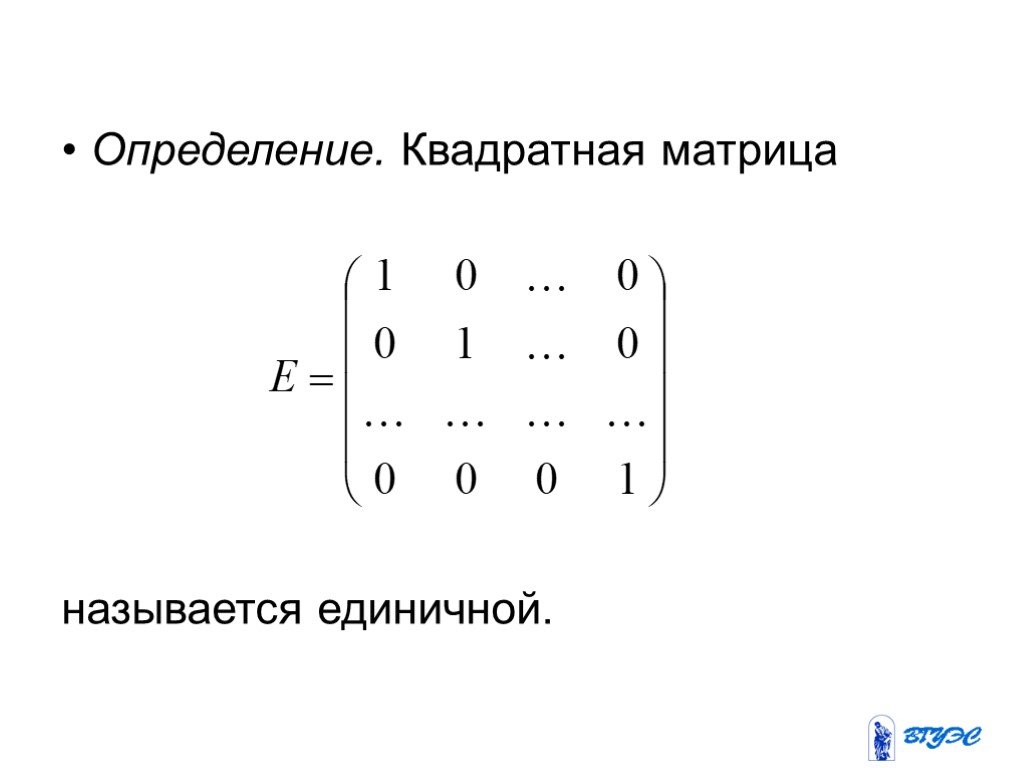
Определение. Квадратная матрица называется единичной.

Если A и E – квадратные матрицы одного размера, то Определение. Определитель, составленный из элементов квадратной матрицы A, называется определителем этой матрицы. Обозначение: A, detA

Определитель произведения квадратных матриц равен произведению определителей этих матриц: A·В= A·В Определение. Квадратная матрица называется невырожденной (неособенной), если её определитель отличен от нуля, и вырожденной (особенной) в противном случае.

Определение. Пусть A – квадратная матрица. Матрица называется обратной к матрице A, если выполняется равенство . Матрицы A и являются взаимно обратными, то есть

Теорема. Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица А была невырожденной. Формула для вычисления обратной матрицы:

Свойства операций над матрицами: А+В = В+А А+(В+С) = (А+В)+С (α+β)А = αА+βА, где α и β – числа α(А+В) = αА+ αВ; (αβ)А = α(βА) А(ВС) = (АВ)С; А(В+С) = АВ+АС А+0 = А АЕ = ЕА = А

Матрицы: квадратная, единичная, нулевая, невырожденная; обратная матрица, определитель матрицы.

Вопросы для самопроверки по теме «Матрицы»

Определения: матрицы, квадратной, единичной, нулевой, невырожденной матриц. Действия над матрицами: сложение, умножение на число, произведение матриц. Свойства операций над матрицами. Определение обратной матрицы, теорема о существовании, нахождение обратной матрицы.

Тема 3. Системы линейных алгебраических уравнений

Пусть дана система m линейных уравнений с n неизвестными: – неизвестные, – коэффициенты при неизвестных, – свободные члены системы.

Определение. Если все свободные члены системы равны нулю, система называется однородной. В противном случае система называется неоднородной. Определение. Совокупность значений неизвестных , при подстановке которых уравнения системы обращаются в равенства, называется решением системы.

Определение. Система называется совместной, если она имеет хотя бы одно решение, в противном случае система называется несовместной. Определение. Система, имеющая единственное решение, называется определенной. Система, имеющая более одного решения, называется неопределенной.

Определение. Матрицей системы называется матрица, составленная из коэффициентов при неизвестных.

Определение. Расширенной матрицей системы называется матрица системы с добавленным к ней столбцом свободных членов.

Теорема (Формулы Крамера). Если определитель матрицы системы n линейных уравнений с n неизвестными отличен от нуля, то система имеет единственное решение, которое находится по формулам где  – определитель матрицы системы, – определитель, полученный из определителя  заменой j-го столбца на столбец свободных членов.

Матричный метод решения систем n линейных уравнений с n неизвестными Обозначим: Если , то

Метод Гаусса решения систем m линейных уравнений с n неизвестными Определение. Две системы называются эквивалентными, если все решения одной системы являются решениями другой, и наоборот.

Элементарные преобразования расширенной матрицы системы, приводящие к эквивалентной системе: 1) перестановка двух строк; 2) умножение элементов какой-либо строки на любое число, отличное от нуля; 3) прибавление к элементам какой-либо строки соответствующих элементов другой строки, умноженных на любое действительное число; 4) исключение из матрицы строки, полностью состоящей из нулей.

Метод Гаусса – метод последовательного исключения неизвестных: с помощью элементарных преобразований система приводится к такому виду, чтобы каждое следующее уравнение системы содержало неизвестных меньше, чем предыдущее.

Теорема Кронекера-Капелли. Для того чтобы система m линейных уравнений с n неизвестными была совместной, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы.

Однородная система линейных уравнений всегда совместна, т. к. имеет по крайней мере одно решение (данное решение называется тривиальным).

Теорема. Для того чтобы однородная система линейных уравнений имела нетривиальное решение, необходимо и достаточно, чтобы ранг матрицы этой системы был меньше числа неизвестных.

Система линейных уравнений, однородная система, неоднородная система; совместная, несовместная, определенная, неопределенная системы; эквивалентные системы, матрица системы, расширенная матрица системы.

Вопросы для самопроверки по теме «Системы линейных уравнений»

Определения: системы линейных уравнений, однородной и неоднородной систем, решения системы, совместной и несовместной систем, определенной и неопределенной систем. Формулы Крамера. Матричный метод решения систем. Метод Гаусса. Теорема Кронекера-Капелли. Решение однородных систем.

Тема 4. Векторная алгебра

Определение. Вектором называется направленный отрезок. Обозначение: (А – начало вектора, В – конец вектора).

Определение. Нулевым вектором называется вектор, начало и конец которого совпадают. Обозначение:

Определение. Расстояние между началом и концом вектора называется его длиной, или модулем. Обозначение:

Определение. Векторы называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Обозначение: векторы сонаправлены векторы противоположно направлены

Определение. Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Определение. Два вектора называются равными, если они сонаправлены и имеют равные длины. Обозначение:

Определение. Два вектора называются противоположными, если они противоположно направлены и имеют равные длины. Обозначение:

Любой вектор в пространстве можно представить в виде где – единичные векторы, направленные соответственно вдоль осей Ox, Oy, Oz (орты осей); – координаты вектора: или

Модуль вектора вычисляется по формуле Если даны точки и , то

Определение. Линейными операциями называют операции сложения и вычитания векторов и умножения вектора на число.

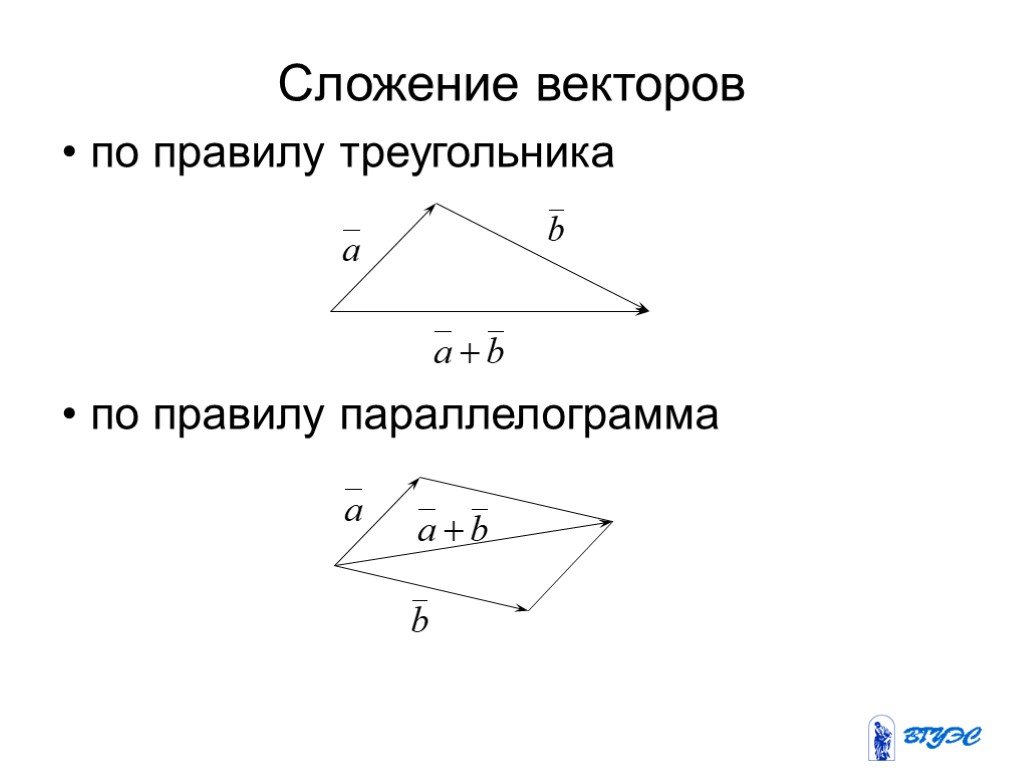
Сложение векторов по правилу треугольника по правилу параллелограмма

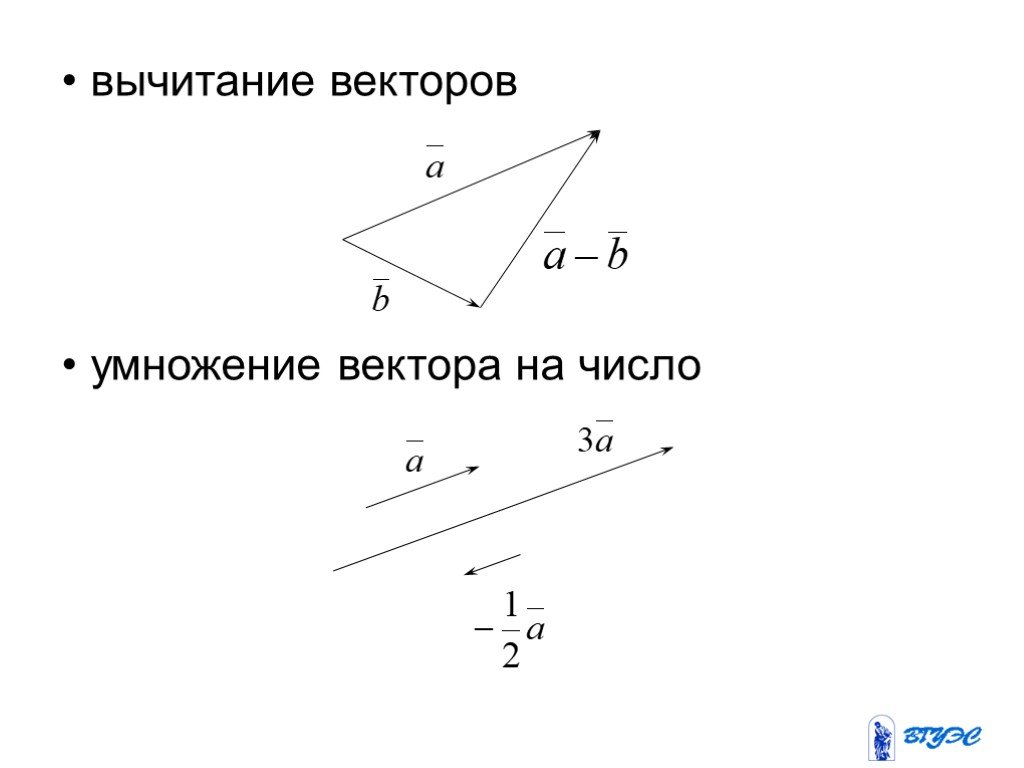
вычитание векторов умножение вектора на число

Если , то 1) 2) 3) 4)

Свойства линейных операций: 1) 2) 3) 4) 5) 6) 7)

Скалярное произведение векторов Определение. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:

Выражение скалярного произведения через координаты перемножаемых векторов:

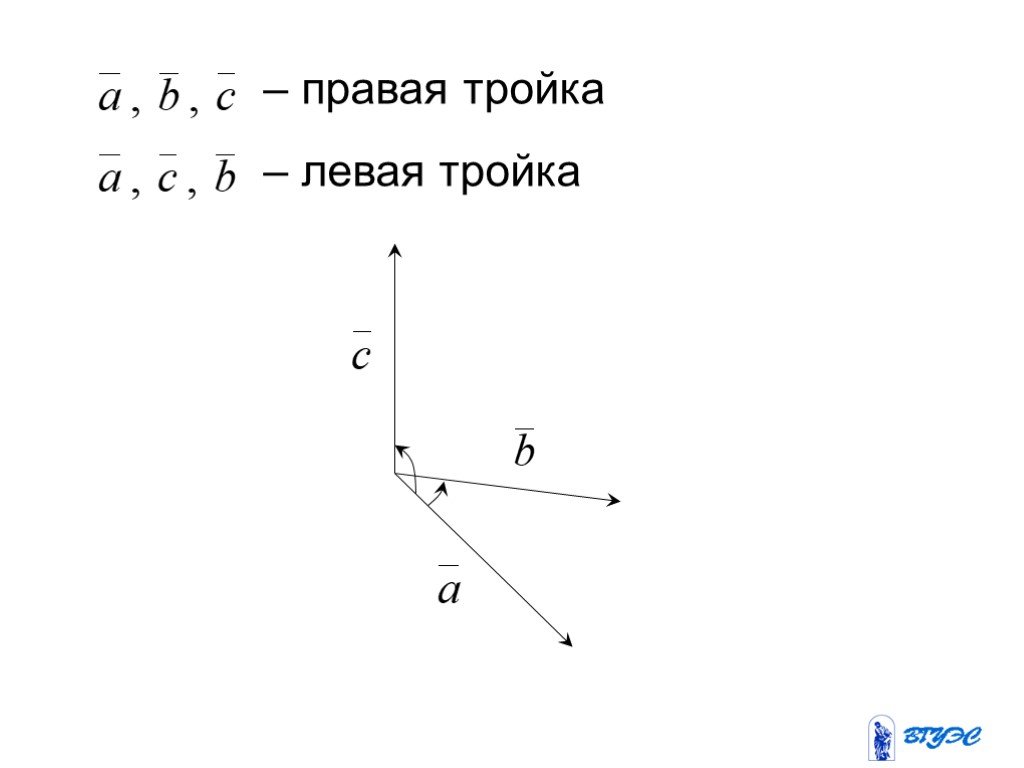
Свойства скалярного произведения: 1) 2) 3) 4) , или , или 5)

Векторное произведение векторов Определение. Упорядоченная тройка некомпланарных векторов называется правой, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки. В противном случае тройка называется левой (начала векторов тройки предполагаются совмещенными).

– правая тройка – левая тройка

Определение. Векторным произведением вектора на вектор называется вектор , удовлетворяющий условиям: 1) 2) 3) векторы образуют правую тройку. Обозначение:

Теорема (геометрический смысл векторного произведения). Модуль векторного произведения двух векторов равен площади параллелограмма, построенного на этих векторах. Следствие.

Выражение векторного произведения через координаты перемножаемых векторов:

Свойства векторного произведения: 1) 2) 3) 4) , или , или 5)

Смешанное произведение векторов Определение. Смешанным, или векторно-скалярным произведением трех векторов называется произведение вида Обозначение:

Выражение смешанного произведения через координаты перемножаемых векторов:

Теорема (условие компланарности трех векторов). Для того чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.

Теорема (геометрический смысл смешанного произведения). Смешанное произведение трех векторов с точностью до знака равно объему параллелепипеда, построенного на этих векторах как на ребрах. Следствие:

Вектор, модуль вектора, коллинеарные векторы, компланарные векторы, координаты вектора; скалярное, векторное, смешанное произведения векторов.

Вопросы для самопроверки по теме «Векторная алгебра»

Дайте определения вектора, нулевого вектора, длины вектора, коллинеарных векторов, компланарных векторов, равных векторов, противоположных векторов. Как определяются сумма векторов, разность векторов, произведение вектора на число? Скалярное, векторное, смешанное произведения векторов: определение, выражение через координаты перемножаемых векторов, свойства. Сформулируйте условия коллинеарности, перпендикулярности, компланарности векторов.

Тема 5. Прямая на плоскости

Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору: – вектор, перпендикулярный прямой (нормальный вектор прямой), – заданная точка на прямой.

Общее уравнение прямой: – вектор, перпендикулярный прямой (нормальный вектор прямой).

Уравнение прямой, проходящей через данную точку параллельно данному вектору (каноническое уравнение прямой): – вектор, параллельный прямой (направляющий вектор прямой), – заданная точка на прямой.

Уравнение прямой, проходящей через две данные точки: – заданные точки на прямой.

Уравнение прямой, проходящей через данную точку в заданном направлении: – угловой коэффициент прямой ( – угол между прямой и осью Ox), – заданная точка на прямой.

Уравнение прямой с угловым коэффициентом: – угловой коэффициент прямой ( – угол между прямой и осью Ox), b – отрезок, отсекаемый прямой на оси Oy.

Угол между двумя прямыми: – угловые коэффициенты прямых.

Условие параллельности двух прямых: Условие перпендикулярности двух прямых: где – угловые коэффициенты прямых.

Расстояние от точки до прямой :

Прямая, параллельные прямые, перпендикулярные прямые, нормальный вектор прямой, направляющий вектор прямой, угловой коэффициент прямой.

Вопросы для самопроверки по теме «Прямая на плоскости»

Различные виды уравнений прямой на плоскости. Какой вектор называется нормальным, направляющим вектором прямой? Как определяется угловой коэффициент прямой? В каком случае k = 0? k не существует? Условия параллельности и перпендикулярности прямых.

Тема 6. Теория вероятностей. Случайные события

Элементы комбинаторики

Определение. Пусть даны n различных элементов. Перестановками из n элементов называются множества, составленные из этих n элементов, отличающиеся друг от друга порядком элементов. Число перестановок:

Определение. Пусть даны n различных элементов. Размещениями из n элементов по k элементов называются множества, составленные из k элементов, выбранных из n данных элементов, отличающиеся друг от друга либо составом элементов, либо их порядком. Число размещений из n элементов по k элементов:

Определение. Пусть даны n различных элементов. Сочетаниями из n элементов по k элементов называются множества, составленные из k элементов, выбранных из n данных элементов, отличающиеся друг от друга лишь составом элементов. Число сочетаний из n элементов по k элементов:

Правило произведения. Если первое действие можно выполнить n количеством способов, а второе действие – k количеством способов, то оба действия можно выполнить n·k количеством способов.

Случайные события

Определение. Достоверным называется событие, которое обязательно произойдет при осуществлении определенной совокупности условий. Определение. Невозможным называется событие, которое заведомо не произойдет при осуществлении определенной совокупности условий.

Определение. Случайным называется событие, которое при осуществлении определенной совокупности условий может либо произойти, либо не произойти. Определение. Каждое осуществление указанной совокупности условий называют испытанием.

Определение. События называются единственно возможными, если появление в результате испытания одного и только одного из них является достоверным событием (говорят, что такие события образуют полную группу).

Определение. События называются равновозможными, если есть основания считать, что ни одно из этих событий не является более возможным, чем другие.

Определение. Каждое событие, которое может наступить в испытании, называется элементарным исходом. Определение. Элементарные исходы, при которых интересующее нас событие наступает, называются благоприятствующими этому событию.

Классическое определение вероятности. Вероятностью события А называется отношение числа благоприятствующих этому событию исходов к общему числу всех единственно возможных и равновозможных элементарных исходов испытания:

Свойства вероятности: 1) Вероятность достоверного события равна 1 (m = n). 2) Вероятность невозможного события равна 0 (m = 0). 3) Вероятность случайного события  вероятность любого события

Определение. Относительной частотой события называется отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний:

Определение. В качестве статистического определения вероятности события принимают относительную частоту события (или число, близкое к ней).

Геометрическое определение вероятности. Пусть на плоскости имеется область G и область g в ней, площади которых равны соответственно. Вероятность того, что точка, брошенная наудачу в область G, попадет в область g, равна

Предполагается, что точка может попасть в любую часть области G, а вероятность попадания в область g пропорциональна лишь ее площади и не зависит ни от расположения, ни от ее формы.

Определение. Суммой двух событий А и В называется событие С, которое состоит в том, что произойдет по крайней мере одно из событий А или В. Обозначение: С = А + В Определение. Суммой нескольких событий называется событие, которое состоит в появлении хотя бы одного из этих событий.

Определение. События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании. В противном случае события называются совместными.

Теорема сложения вероятностей несовместных событий. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

Теорема. Сумма вероятностей событий, образующих полную группу, равна единице:

Определение. Два единственно возможных события, образующих полную группу, называются противоположными. Обозначение: Теорема. Сумма вероятностей противоположных событий равна единице:

Определение. Произведением двух событий А и В называется событие С, которое состоит в совместном появлении событий А и В. Обозначение: С = А · В Определение. Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Определение. Два события называются независимыми, если вероятность одного из них не зависит от появления или непоявления другого. В противном случае события называются зависимыми.

Теорема умножения вероятностей независимых событий. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

Определение. Несколько событий называются независимыми в совокупности, если каждое из них и любая комбинация остальных событий есть события независимые.

Следствие. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

Определение. Условной вероятностью называется вероятность события В, вычисленная в предположении, что событие А уже наступило. Обозначение:

Теорема умножения вероятностей зависимых событий. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

Следствие. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:

Формула полной вероятности. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий , образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

Формулы Байеса. Пусть событие А может наступить лишь при условии появления одного из несовместных событий , образующих полную группу. Допустим, произведено испытание, в результате которого появилось событие А. Тогда вероятности гипотез вычисляются по формулам:

Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0

Перестановки, размещения, сочетания, испытание; невозможное, достоверное, случайное события; вероятность, условная вероятность, сумма и произведение событий, совместные и несовместные события, зависимые и независимые события.

Вопросы для самопроверки по теме «Случайные события»

Определение перестановок, размещений, сочетаний. Достоверное, невозможное, случайное события. Классическое, геометрическое, статистическое определения вероятности. Сумма и произведение событий. Теоремы сложения и умножения вероятностей. Формула полной вероятности. Формулы Байеса. Формула Бернулли.

Тема 7. Случайные величины

Определение. Случайной величиной называется величина, которая в результате испытания примет одно и только одно числовое значение, заранее неизвестное. Обозначение: X , Y

Определение. Дискретной называют случайную величину, которая принимает отдельные изолированные значения. Число значений может быть конечным или бесконечным.

Определение. Непрерывной называют случайную величину, которая может принять любое значение из некоторого интервала. Число значений непрерывной случайной величины бесконечно.

Дискретные случайные величины

Определение. Законом распределения дискретной случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями.

Закон распределения дискретной случайной величины можно задать табличным, графическим и аналитическим способами.

Определение. Рядом распределения дискретной случайной величины называется таблица, в верхней строке которой перечислены принимаемые значения, а в нижней – соответствующие вероятности.

Графический способ. Определение. Многоугольником распределения называется ломаная, с вершинами в точках

Аналитический способ. Определение. Функцией распределения вероятностей случайной величины X называют функцию , определяющую для каждого значения x вероятность того, что случайная величина X примет значение, меньшее x, т.е.

Свойства функции распределения дискретной случайной величины: 1) 2) – неубывающая функция 3) 4) Если a – наименьшее значение случайной величины, b – наибольшее значение, то

Числовые характеристики дискретных случайных величин

Определение. Математическим ожиданием дискретной случайной величины X называется сумма произведений всех возможных значений случайной величины на соответствующие вероятности появления этих значений. Обозначение: M(X)

Определение. Две случайные величины называются независимыми, если закон распределения вероятностей одной из них не зависит от того, какие возможные значения приняла другая случайная величина.

Свойства математического ожидания ДСВ: 1) Математическое ожидание постоянной величины равно самой постоянной: 2) Постоянный множитель можно вынести за знак математического ожидания:

Свойства математического ожидания ДСВ (продолжение): 3) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых: 4) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

Определение. Дисперсией дискретной случайной величины X называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Обозначение: D(X)

Свойства дисперсии ДСВ: 1) Дисперсия постоянной величины равна нулю: 2) Постоянный множитель можно вынести за знак дисперсии, предварительно возведя его в квадрат:

Свойства дисперсии ДСВ (продолжение): 3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий слагаемых: Следствие:

Теорема. Дисперсия дискретной случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:

Определение. Средним квадратическим отклонением дискретной случайной величины X называется квадратный корень из ее дисперсии. Обозначение:

Дискретная случайная величина, непрерывная случайная величина, ряд распределения, многоугольник распределения, функция распределения вероятностей, математическое ожидание, дисперсия, среднее квадратическое отклонение.

Вопросы для самопроверки по теме «Случайные величины»

Определения случайной величины, дискретной и непрерывной случайной величины. Способы задания дискретных случайных величин. Ряд распределения, многоугольник распределения. Функция распределения, ее свойства. Числовые характеристики: математическое ожидание, дисперсия, среднее квадратическое отклонение.

Рекомендуемая литература

1. Дубинина Л.Я., Никулина Л.С., Пивоварова И.В. Курс лекций по высшей математике. Часть 1. – Владивосток: Изд-во ВГУЭС, 2008. – 132 с. 2. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Высшая школа, 2004. – 576 с. 3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2004. – 400 с. 4. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2004. – 368 с. 5. Сборник задач по высшей математике / Сост. И.В. Пивоварова, Л.Я. Дубинина, Л.С. Никулина. – Владивосток: ВГУЭС, 2008. – 87 с.

Использование материалов презентации Использование данной презентации может осуществляться только при условии соблюдения требований законов РФ об авторском праве и интеллектуальной собственности, а также с учетом требований настоящего Заявления. Презентация является собственностью авторов. Разрешается распечатывать копию любой части презентации для личного некоммерческого использования, однако не допускается распечатывать какую-либо часть презентации с любой иной целью или по каким-либо причинам вносить изменения в любую часть презентации. Использование любой части презентации в другом произведении, как в печатной, электронной, так и иной форме, а также использование любой части презентации в другой презентации посредством ссылки или иным образом допускается только после получения письменного согласия авторов.