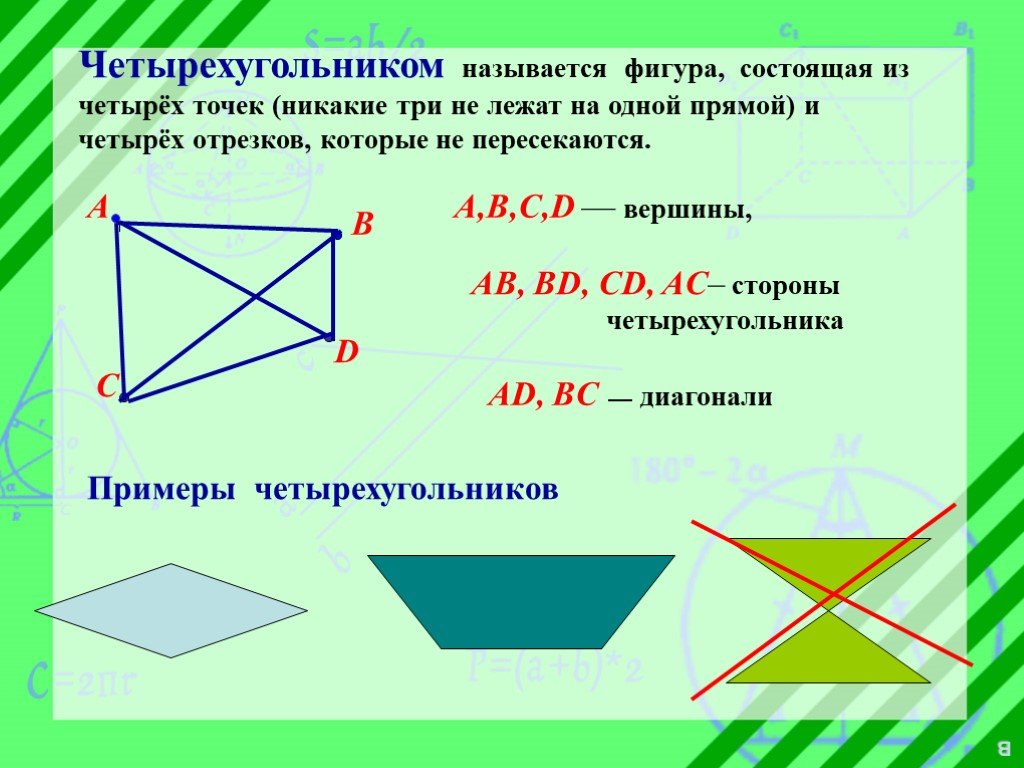
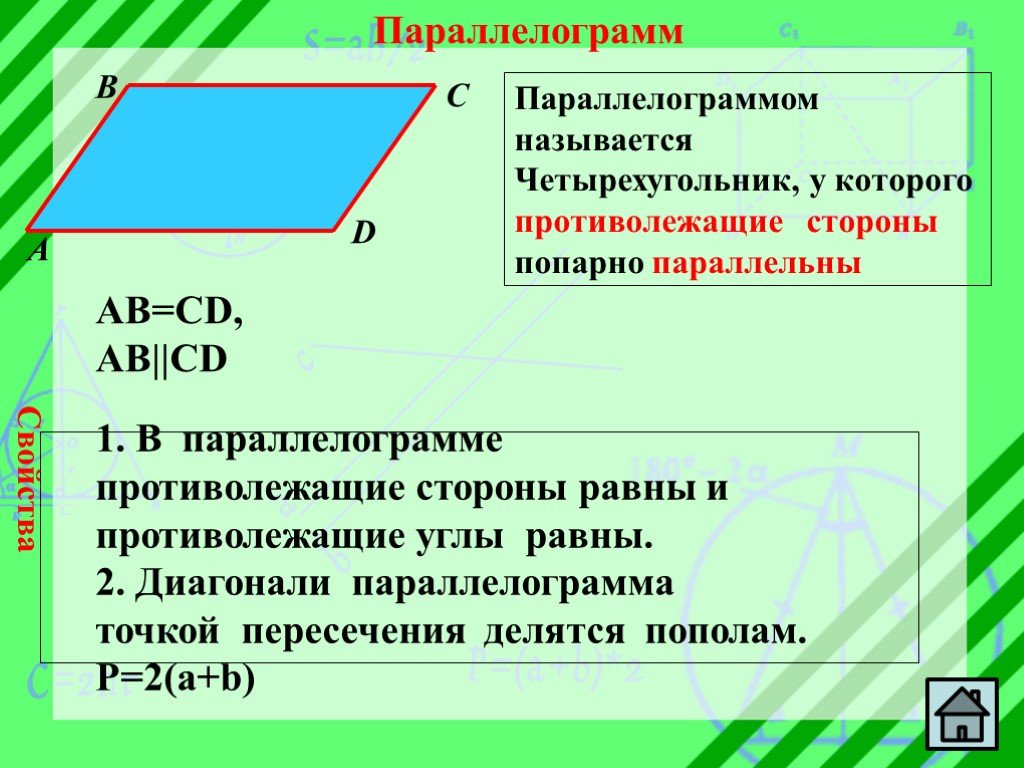
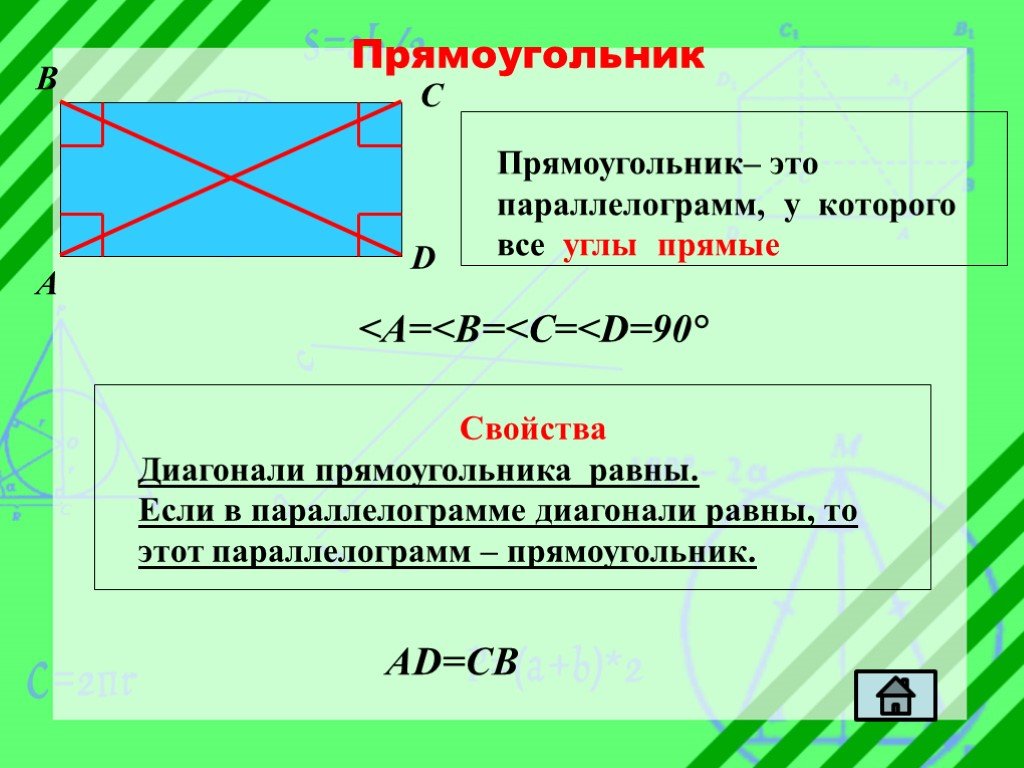
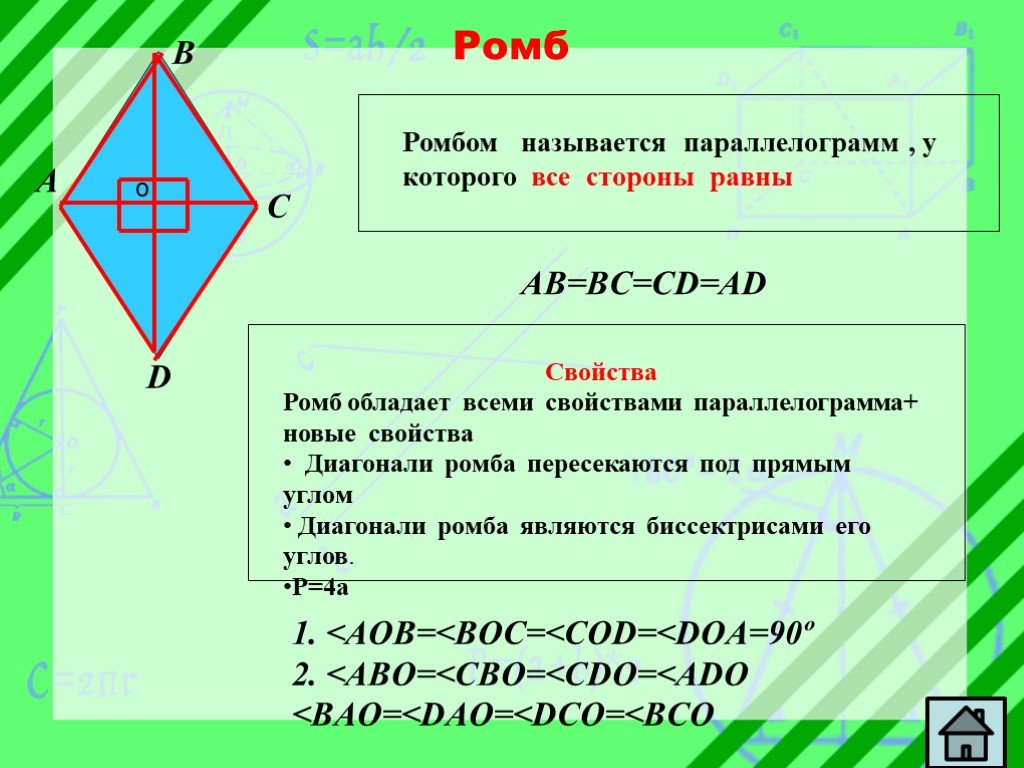
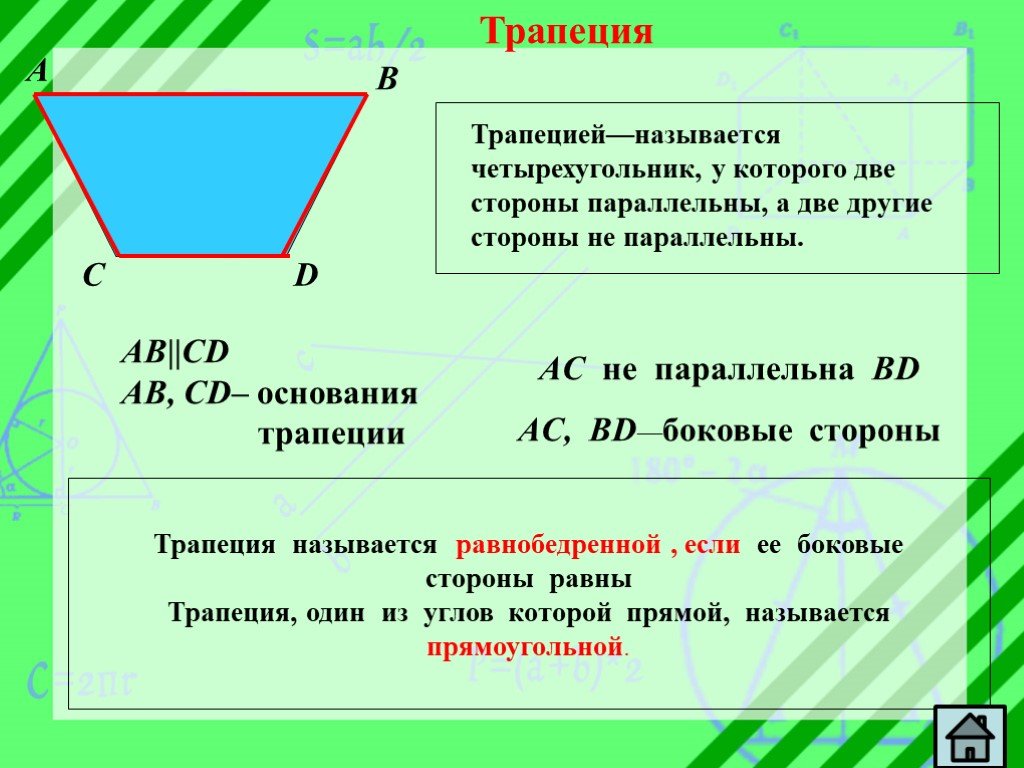
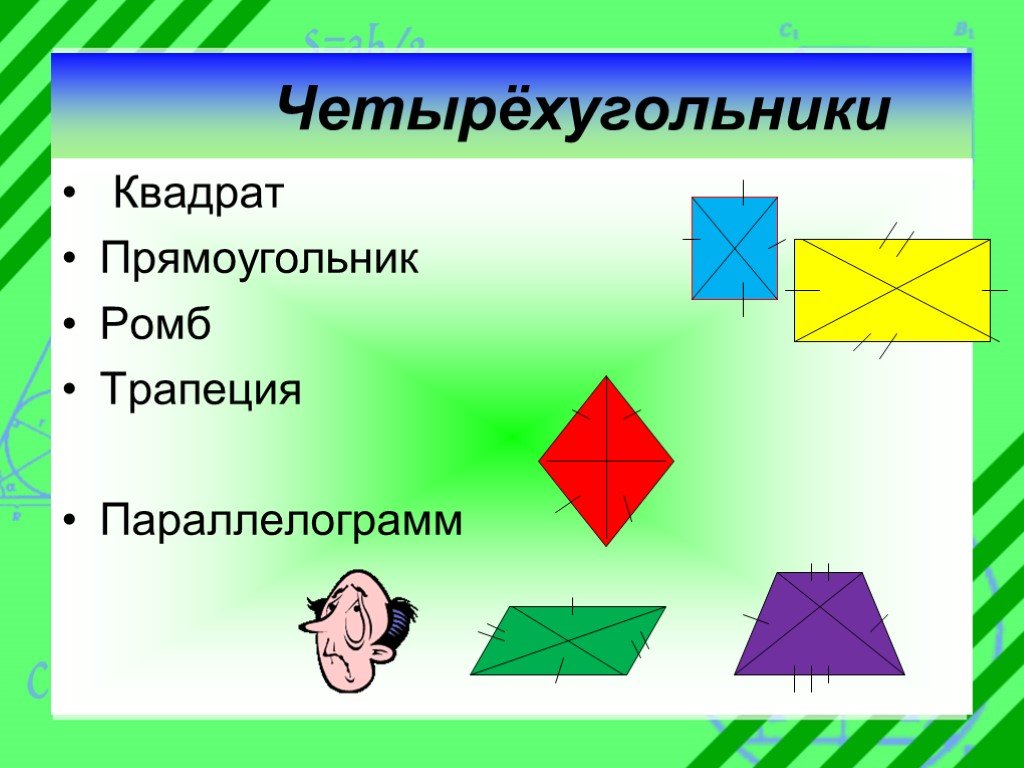
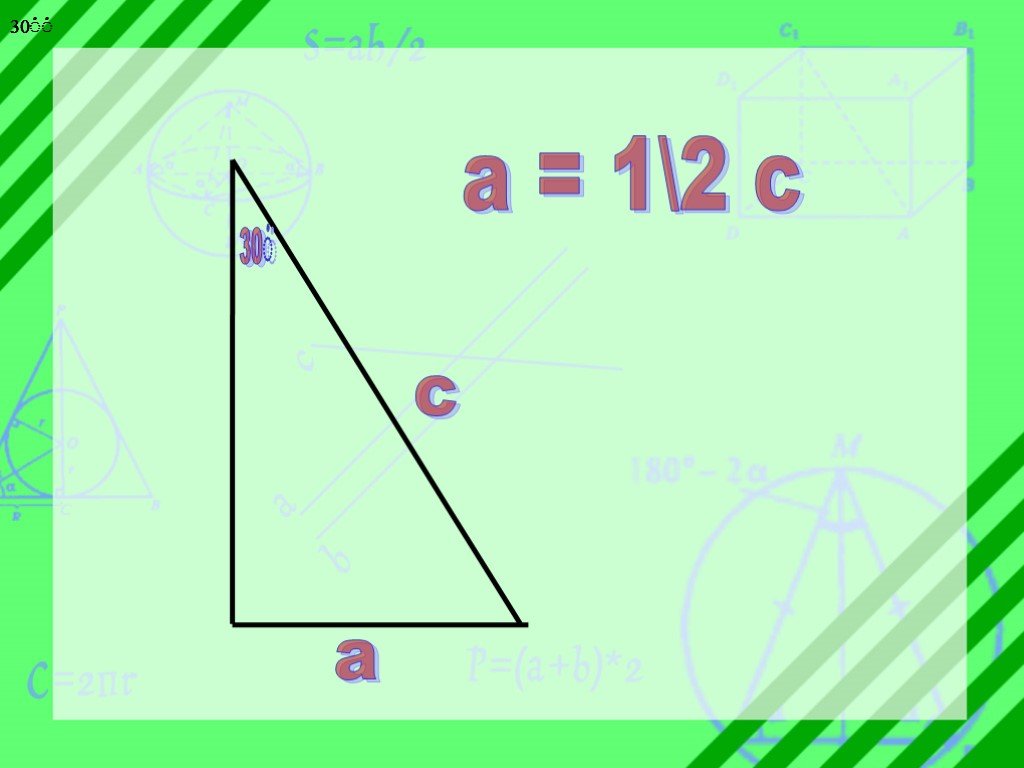
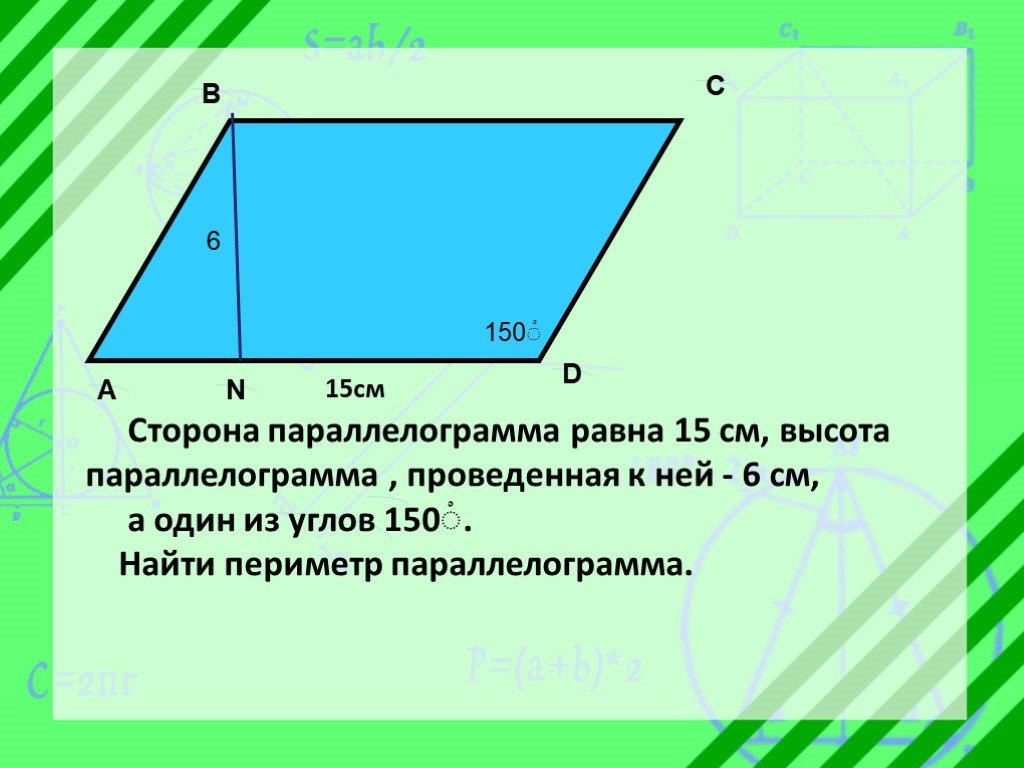
Презентация "Из жизни четырёхугольников" по математике – проект, доклад
Презентацию на тему "Из жизни четырёхугольников" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 22 слайд(ов).
Слайды презентации
Список похожих презентаций
Квадрат в жизни
(Автор неизвестен). Пришёл из школы старший брат, Из спичек выложил квадрат. Дала мне мама шоколад, Я дольку отломил - квадрат. И стол -квадрат, и ...Без математики, друзья, в жизни нам никак нельзя
Актуальность. Математика находится в тесной связи со всеми естественными, гуманитарными, точными науками и др., математические знания применяются ...Закрепление и обобщение изученного материала. Здоровый образ жизни
Тема:. Закрепление и обобщение изученного материала. Здоровый образ жизни. I Этап. Устный счёт. 68 – 39 12 х 6 90 : 3 54 – 38. 26 + 15 23 х 3 32 – ...Золотое сечение в математике и в жизни
« В геометрии существует два сокровища – теорема Пифагора и деление отрезка в крайнем и среднем отношении. Первое можно сравнить с ценность золота, ...Геометрия в нашей жизни
«Визитная карточка» проекта. Класс – 7 Цели проекта: 1. Мотивировать изучение геометрии, как науки, создающие математические модели окружающей действительности. ...Геометрия в жизни Многогранники
Александрийский маяк. В 285 году до н.э.на острове Фарос архитектор Сострат Книдский приступил к строительству маяка. Маяк строился пять лет и получился ...Геометрия в жизни
содержание. ВСТУПЛЕНИЕ ИСТОРИЧЕСКИЕ СВЕДЕНИЯ УГАДАЙ-КА ЦИЛИНДР КОНУС ПРЯМЫЕ и ПЛОСКОСТИ ШАР ПИРАМИДА ИТОГ О СЕБЕ. «Не будь в природе твердых тел, ...Золотое сечение и применение золотого сечения в жизни
Цель работы:. 1.Изучить тему «золотая пропорция». 2.Рассмотреть связанные с нею отношения. 3.Познакомиться с «золотой пропорцией» в природе. Методы ...Великий мыслитель (страницы жизни Н.И. Лобочевского)
Николай Иванович Лобачевский. Николай Иванович Лобачевский родился 1 декабря (20 ноября) 1792 года в Нижнем Новгороде в бедной семье мелкого чиновника. ...Использование геометрических фигур в реальной жизни
. Произведение инженерного искусства. Египетские пирамиды. . Одно из самых высоких зданий в Европе. Мост. Разводной мост. Одно из самое больших колес ...Во всем ли в жизни должна быть
Спасем осла ! Классическую постановку вопроса о право-левой симметрии приписывают средневековому философу Буридану. Он сформулировал следующую проблему. ...Использование параллелограмма в жизни
Параллелограмм в жизни –. – это рамы велосипедов, мотоциклов, где для жесткости проведена диагональ. В физике параллелограмм применяют при изучении ...Из истории математики… Геометрия
Возникновение науки. Первые геометрические представления у людей возникли очень ,очень давно. Для первобытных людей важную роль играла форма окружающих ...Из чего строится геометрия?
Если вообразить геометрию в виде огромного дома, то ученых, чьими трудами возведен этот дом, сравнить с каменщиками. Каждое утверждение опирается ...Из истории числительных
Когда возникла потребность точного подсчета, люди стали считать и десятками. Десять стало главным словом. Числа от 11 до 19 так и образовались: один ...Из истории позиционных систем счисления
Позиционные системы счисления. В позиционных системах счисления количественное значение цифры зависит от её позиции в числе. Наиболее распространенными ...Из истории обыкновенных дробей
Дробь – это число, состоящее из частей единицы. Что такое дробь ? Необходимость в дробных числах возникла в результате практической деятельности человека. ...Из истории обыкновенных дробей
Есть такая дробь у нас, Про неё пойдет весь сказ, Она из чисел состоит, А между ними, как мосточек, Дробная черта лежит, Над чертою числитель, Знайте, ...Из истории мер длины
С глубокой древности наши предки измеряли расстояние собой, своим телом. Это и удобно, и руки с ногами всегда при тебе, их нельзя "забыть дома". Система ...Из истории логарифмов
С точки зрения вычислительной практики, изобретение логарифмов по возможности можно смело поставить рядом с другим, более древним великим изобретением ...Конспекты
Математика в нашей жизни
Открытый урок для родителей. «Математика в нашей жизни». Цели:. образовательные:. формирование устойчивого интереса к математике;. . ...Математическая статистика в жизни класса
. Тема урока: «Математическая статистика в жизни класса». Цели. :. Образовательные:. . Обобщение и систематизация знаний по обработке информации, ...Комбинаторика в нашей жизни
Разработка урока по математике в 6 классе. Учи. тель: Седлина Лариса Михайловна. Место работы: ГБОУ СОШ с. Новодевичье м/р Шигонский Самарской ...История возникновения чисел. Магическое значение чисел в нашей жизни
. Научно-практическая конференция школьников. . «Шаг в науку». секция «Математика». . История возникновения чисел. ...Графы в нашей жизни
Тема: Графы в нашей жизни. Класс. : 10. Цели урока:. . Образовательные. : усвоение новых знаний, закрепление практических умений;. . ...Из истории математики
Урок математики в 5 классе. «Из истории математики». . . При проведении урока необходимо иметь карту, на которой обозначены Греция, Египет Россия, ...Из истории геометрии
Урок геометрии в 7 классе «Из истории геометрии». Вовденко Ольга Леонидовна. ,. учитель математики. . МБОУ СОШ № 61 им. М.И. Неделина. . г. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:12 февраля 2019
Категория:Математика
Содержит:22 слайд(ов)
Поделись с друзьями:
Скачать презентацию