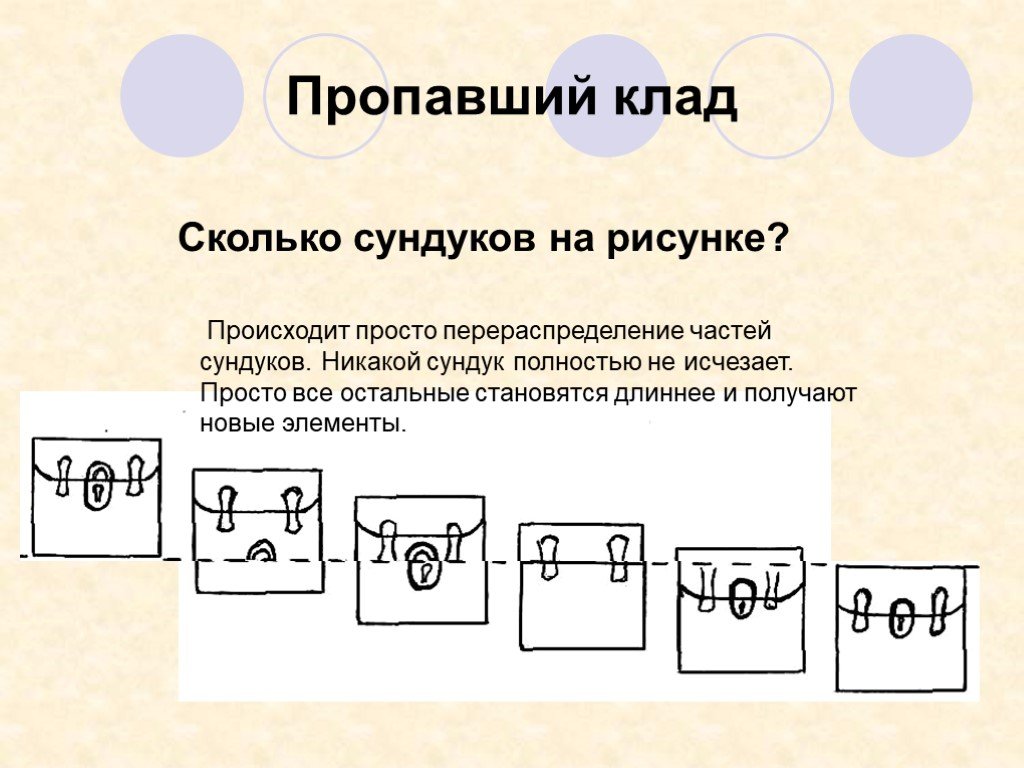
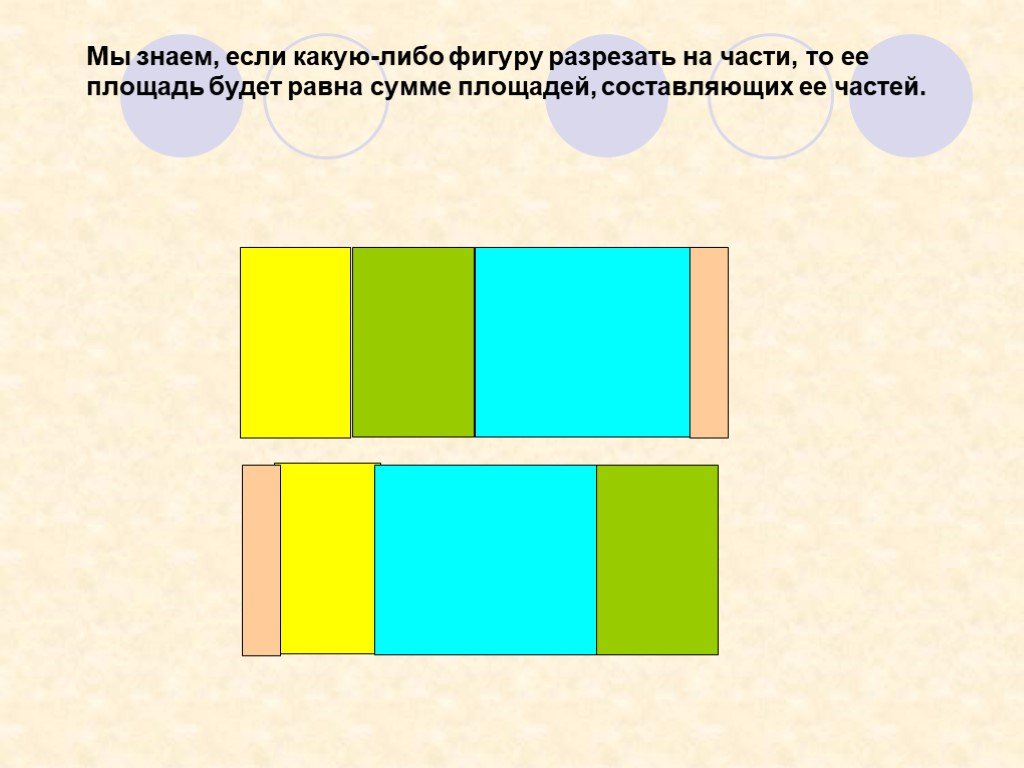
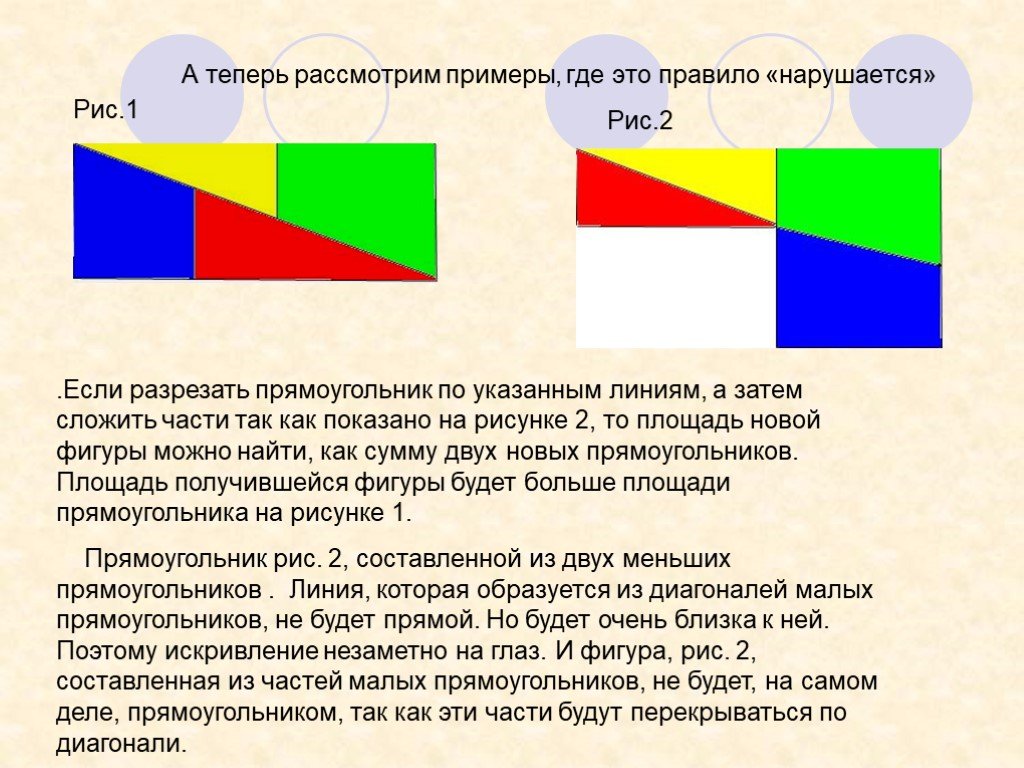
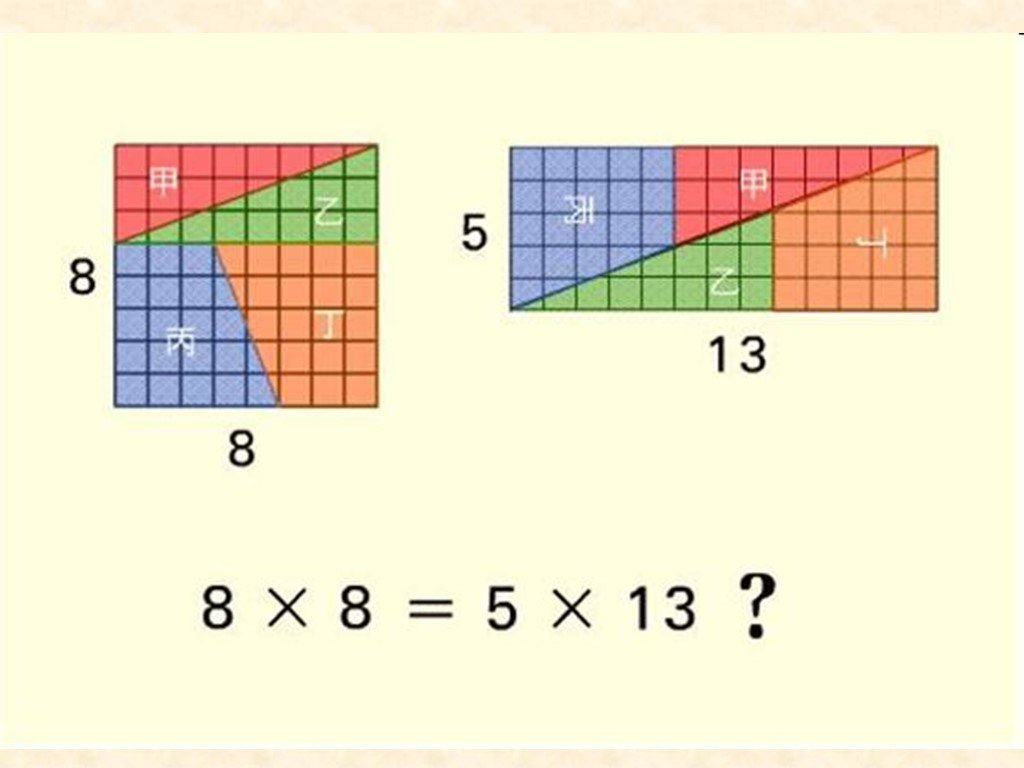
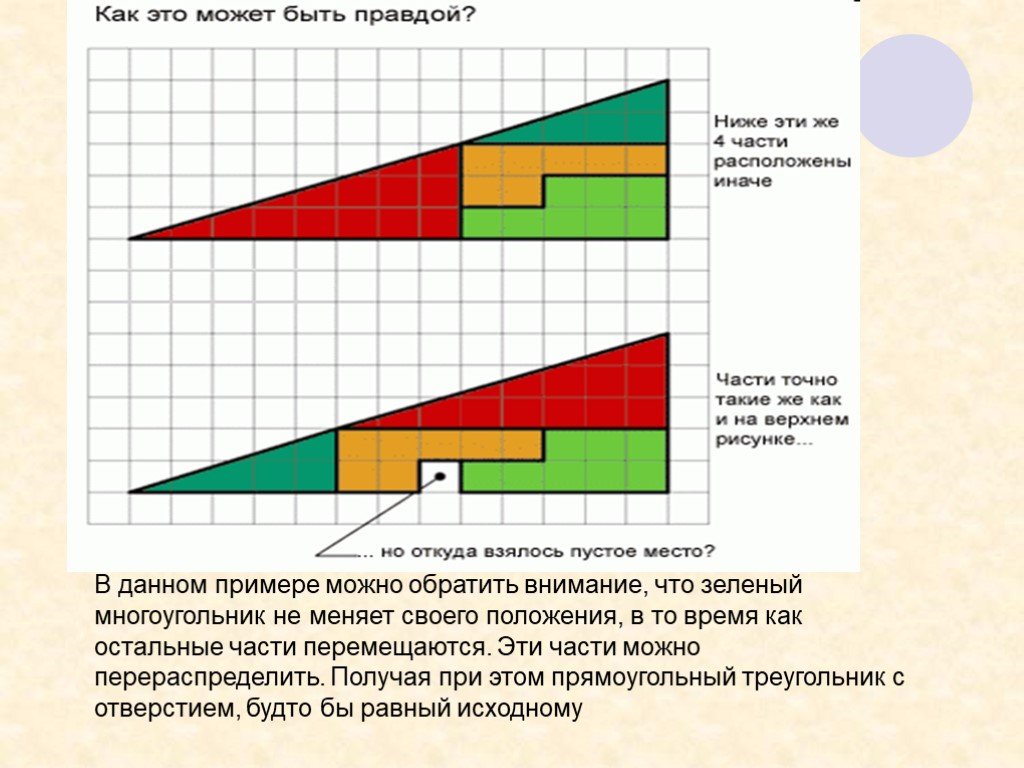
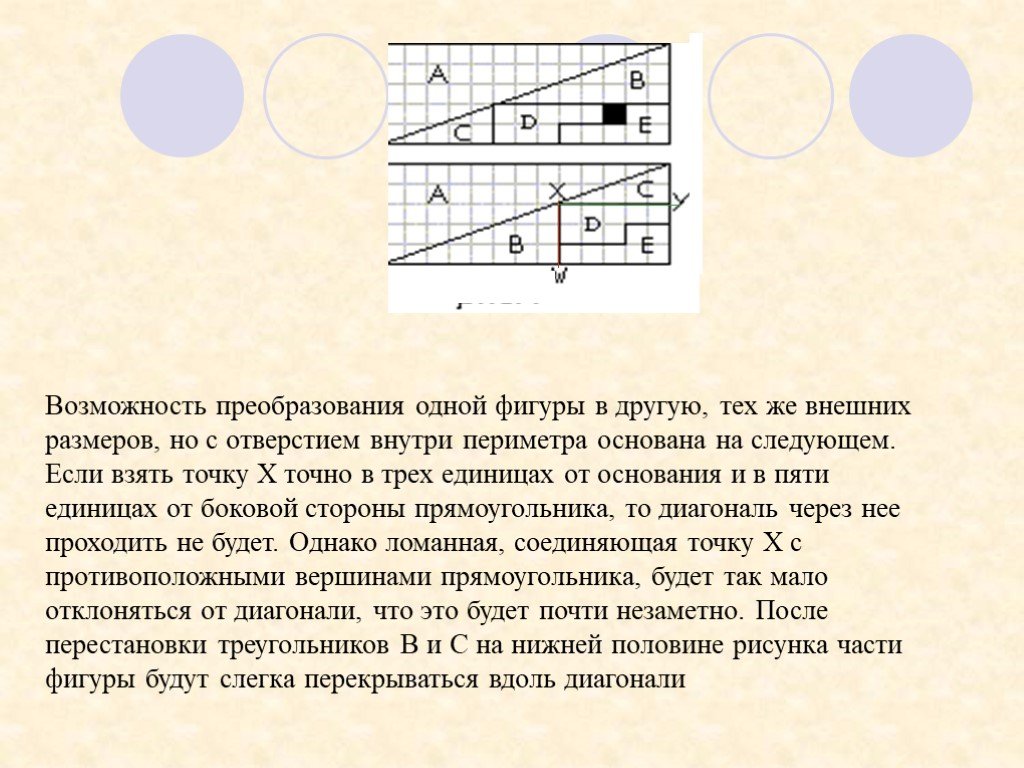
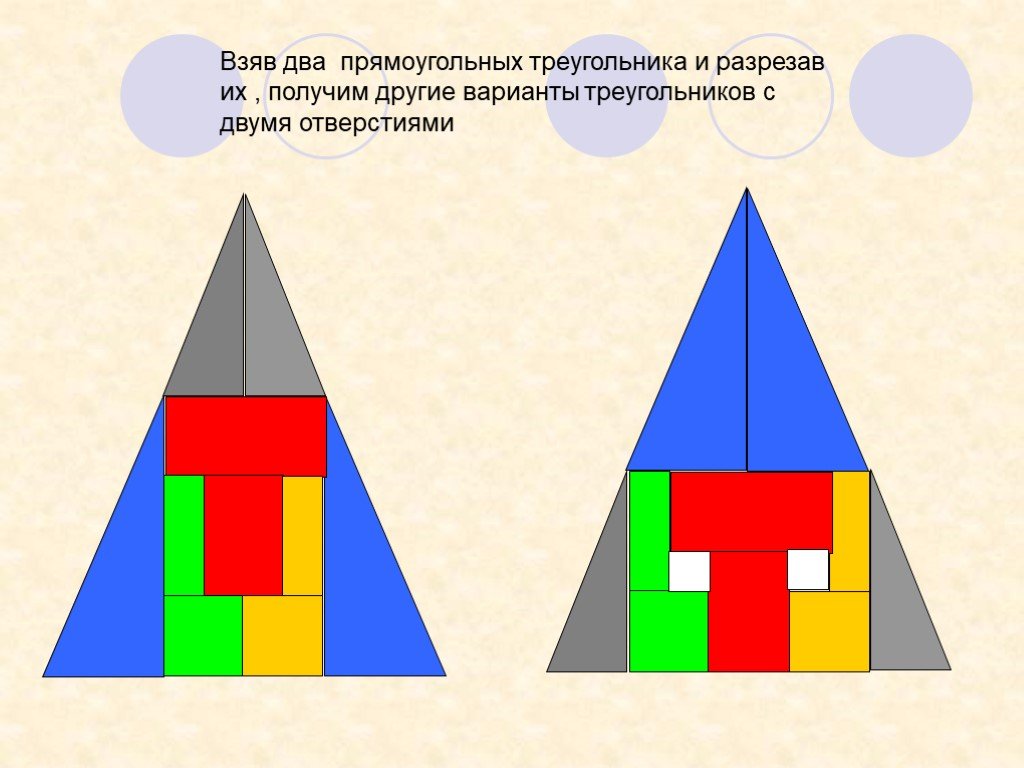
Презентация "Не верь глазам своим" (6 класс) по математике – проект, доклад
Презентацию на тему "Не верь глазам своим" (6 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 21 слайд(ов).
Слайды презентации
Список похожих презентаций
«Задачи по математике»
Успех каждого – это шаг к успеху всего класса. Реши примеры 5 ·8 5·5 4·6 8·8 25-5 36-6. 48-8 99-9 6·10 50·10 4·10 7·100. =40 =25 =24 =64 =20 =90 =60 ...Авторские задачи по математике и физике, составленные по повести Н.В. Гоголя «Ночь перед Рождеством
Методологическая основа: Класс арифметических задач огромен. Учащиеся старших классов обычно пытаются решать такие задачи алгебраически, так как владеют ...Внеклассное мероприятие по математике для 8 класса Отличники
1. Способствование проявлению интеллектуальных способностей учащихся. 2. Активизации познавательной деятельности учащихся. 3. Формирование навыков ...«Моя математика» - задачи на нахождение целого или части
МАТЕМАТИКА 1 3 4 5 7 6 8 9 0. Работа с числовым рядом. http://www.bajena.com/ru/kids/mathematics/sum-mathematics.php. 1. Прочитайте текст справа и ...Внеклассное мероприятие по математике "Своя игра
Первый раунд. Разминка. Второй раунд. Шевели извилинами. Финальный раунд. «Математика – царица наук, арифметика – царица математики». Назовите автора ...Башни Кремля. Задачи по математике
Башни Кремля. Спасская башня считается самой красивой и стройной башней. Построена в 1491 году под руководством архитектора Пьетро Антонио Солари ...Внеклассное мероприятие по математике в 8 классе.
I. БЛИЦ-ЗНАКОМСТВО. КАЖДОЙ ИЗ КОМАНД БУДЕТ ЗАДАНО ПО 15 ВОПРОСОВ. ЗА КАЖДЫЙ ПРАВИЛЬНЫЙ ОТВЕТ КОМАНДА ПОЛУЧАЕТ 1 БАЛЛ. ВОПРОСЫ ДЛЯ ПЕРВОЙ КОМАНДЫ. ...Внеклассная работа по математике
Цель внеклассной работы по математике:. Всестороннее развитие и социализация ученика на основе усвоения математических знаний и умений, необходимых ...Внеклассное мероприятие по математике "Своя игра"
1 раунд. Команды составляют слова из математического термина. За 1 минуту составьте как можно больше слов из слова. стереометрия. 2 раунд. Команды ...Внеклассное занятие по математике.
Учился в Туринском университете. Стал профессором геометрии в Артиллерийской школе Турина. 1754г. - профессор в артиллерийской школе Турина 1759г. ...Внеклассное мероприятие по математике
школьная жизнь. Предметная неделя естественно-математического цикла. Срок проведения с 13.02.2012 по 20.02.2012 года. Утром 16 февраля на дверях кабинетов ...береза глазами математика
Цель. Целью данного исследования является выявление в повседневной жизни различных законов, которым нас обучают еще в школе. И как же все можно связать ...Внеклассное мероприятие по математике
Определения 20. Дайте определение натуральных чисел. ответ. Натуральные числа - это числа, которые используют при счёте предметов. Определения 40. ...внеклассная математика
Испытание №1 Домик Лесовичка. «Посмотрите внимательно на мой домик и скажите, из чего он состоит». «Правильно! Мой домик Состоит из геометрических ...«Уравнения по математике»
17.10.12. Классная работа. Тема: «Уравнения». Решение уравнений. Математические фокусы. Составление равенств. «Секретная» сказка. «Математику нельзя ...Алгоритмы внутренних точек с приближенным решением вспомогательной задачи
1939 – линейное программирование (Канторович). 1947 – симплекс-метод (Данциг). 1967 – метод внутренних точек (Дикин). 1984 – полиномиальный МВТ (Кармаркар). ...Апробация инструментария диагностических исследований профессиональной компетентности учителей начальных классов по математике
Проводится в соответствии приказом управления образования и науки области от 18.03.2010 №841 «О проведении апробации инструментария диагностического ...Анализ обучающих программ по математике 1-4 класс
Интерактивная математика для 1-4 классов. Программа фирмы Marco Polo Group. Описание продукта: Интерактивный тренажер по математике для начальной ...Анализ контрольной работы по математике на тему "Натуральные числа и шкалы"
Натуральные числа и шкалы. 5 к л а с с № 1. Цели деятельности учителя. Главная дидактическая цель : организовать деятельность учащихся, направленную ...альбом по математике
Формирование базовых знаний, умений и навыков должно быть связано с творческой деятельностью, с развитием индивидуальных задатков учащихся, их познавательной ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:3 декабря 2018
Категория:Математика
Содержит:21 слайд(ов)
Поделись с друзьями:
Скачать презентацию