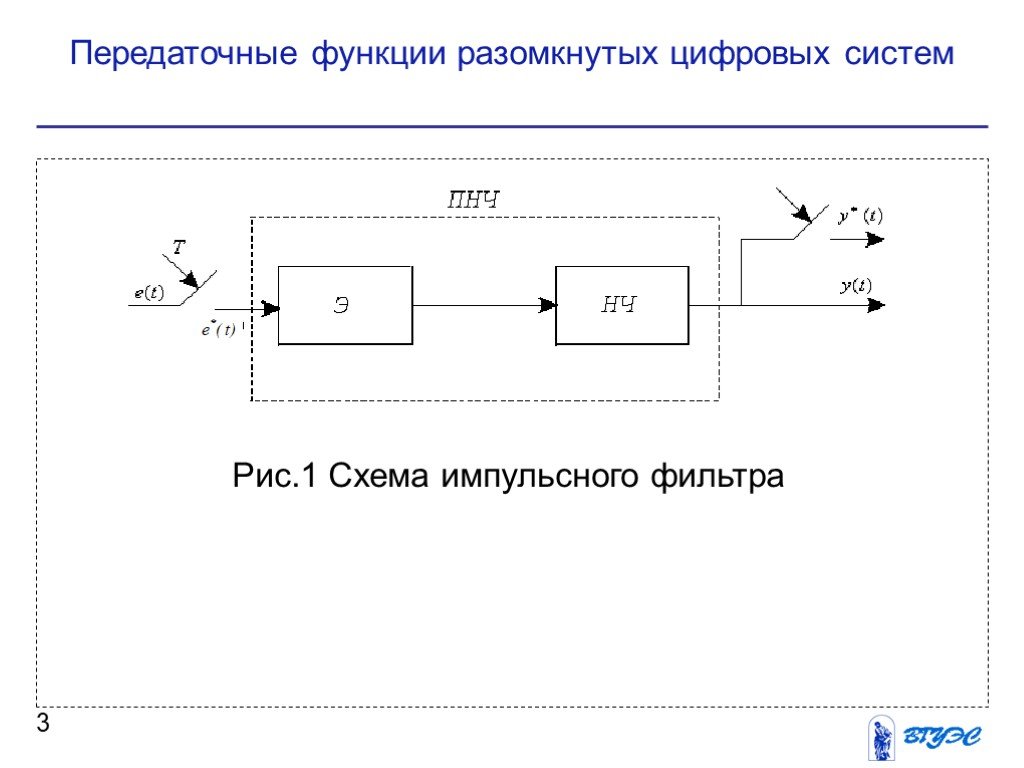
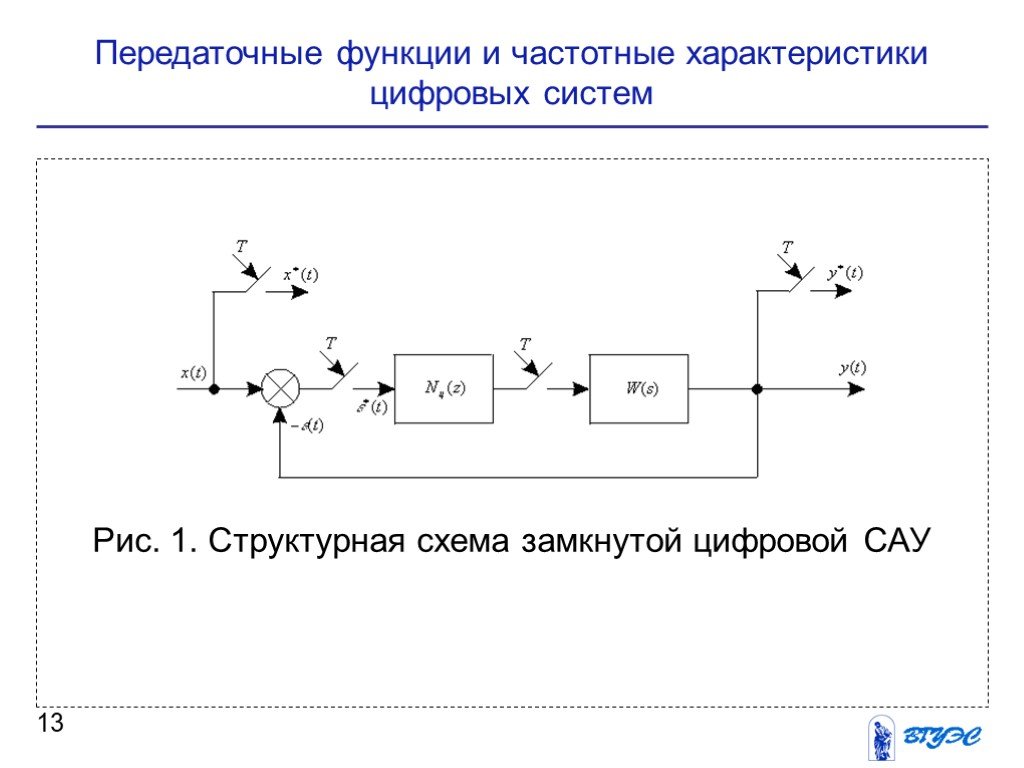
Презентация "Передаточные функции разомкнутой и замкнутой цифровых систем управления" по экономике – проект, доклад

Передаточные функции разомкнутой и замкнутой цифровых систем управления. Получение дискретной передаточной функции из непрерывной передаточной функции. Частотные характеристики цифровых систем

Кафедра ИСКТ Преподаватель Кривошеев В.П.

Передаточные функции разомкнутых цифровых систем

Найдем передаточную функцию системы, структурная схема которой показана на рис. 1. Подобные системы называют импульсными фильтрами. Импульсный фильтр состоит из объекта управления, непрерывной части, формирующего элемента и дискретизатора. Непрерывная часть и формирующий элемент образуют приведенную непрерывную часть импульсного фильтра, на вход которой подаются мгновенные импульсы

Рис.1 Схема импульсного фильтра

Выходной сигнал импульсного фильтра равен сумме реакций приведенной непрерывной части от каждого мгновенного импульса: (1) Следует иметь в виду, что сигнал на выходе импульсного фильтра является непрерывным и не равным нулю между дискретными моментами времени. Введем последовательность мгновенных импульсов выходного сигнала. С этой целью условно подключим к выходу фильтра фиктивный дискретизатор, работающий синхронно с основным дискретизатором импульсного фильтра.

Если квантование входного и выходного сигналов осущест­вляется синхронно, при имеем: (2) (3) Подставляя уравнение (2) в (3), получаем (4) Подстановкой уравнение (4) приводится к виду: (5)

Преобразование уравнения (5) дает: (6) , (7) где - весовая последовательность системы, а выражение (7) является по определению Z-преобразованием функции и . (8) Теперь преобразование выхода, определяемое уравнением (6), можно записать в виде: (9)

Уравнение (9) связывает импульсный выход системы с ее входом. В уравнении (9) функция , которая является отношением выхода к входу , (10) называется импульсной передаточной функцией или Z-передаточ­ной функцией импульсной системы. Следовательно, импульсная передаточная функция может быть определена как отношение Z-преобразований импульсного выхода системы к Z-преобразованию ее импульсного входа.

Передаточная функция приведенной непрерывной части (импульсного фильтра) имеет вид: (11) где Wн(s) – передаточная функция непрерывной части фильтра. Уравнению (11) соответствует импульсная переходная функция (12) где: – переходная функция непрерывной части фильтра.

Дискретная передаточная функция характеризует процессы, происходящие в импульсном фильтре только в дискретные моменты времени. Для анализа характеристик между этими моментами времени используется смещенная дискретная передаточная функция, которая равна Z-преобразованию смещенной импульсной переходной функции приведенной непрерывной части фильтра. Для образования смещенной импульсной переходной функции необходимо в цепь фиктивного дискретизатора включить звено запаздывания с передаточной функцией

Cмещенная дискретная передаточная функция импульсного фильтра определяется как (13) где – cмещенная импульсная переходная функция приведенной непрерывной части фильтра. Придавая  значение от нуля до единицы, можно определить смещенные передаточные функции (13), которые позволяют оценить процессы в импульсном фильтре для различных дискретных моментов времени.

Пример

Найти передаточную функцию реверсивного счетчика без сброса, который накапливает поступающие на его вход положительные и отрицательные импульсы. Счетчик является цифровым интегратором и описывается разностным уравнением: где – дискретные значения выходного и входного сигналов. Решение. Применим к уравнению Z-преобразование. В результате с учетом теоремы (…) найдем, что В соответствии с (9) передаточная функция счетчика

Передаточные функции и частотные характеристики цифровых систем

Рассмотрим структурную схему замкнутой цифровой САУ (Рис. 1), в которой цифровой фильтр с передаточной функцией является последовательным корректирующим устройством. Передаточные функции замкнутой системы определяются так же, как и в непрерывных системах: (14) где – передаточная функция разомкнутой системы.

Рис. 1. Структурная схема замкнутой цифровой САУ

Полученные передаточные функции применяются для анализа устойчивости и качества работы цифровых систем. При определении смещенной передаточной функции замкнутой системы следует учитывать, что звено запаздывания, с помощью которого учитывается смещение во времени, подключается на выходе системы к цепи фиктивного дискретизатора. (15) где – смещенная передаточная функция разомкнутой системы.

Цифровые САУ, так же как и непрерывные системы, в зависимости от ошибки в установившемся режиме подразделяются на статические и астатические. Ошибка в установившемся режиме в дискретные моменты времени находится по теореме о конечном значении . При входном сигнале (16)

Ошибку, определяемую по (3), считают статической. Если эта ошибка не равна нулю, то цифровую систему называют статической, в противном случае система относится к классу астатических. Из уравнения (3) следует, что в астатической системе передаточная функция ошибки равна нулю в точке z=1, что выполняется, если передаточная функция разомкнутой системы в соответствии с (1) имеет полюс в этой же точке.

Ошибку, определяемую по (3), считают статической. Если эта ошибка не равна нулю, то цифровую систему называют статической, в противном случае система относится к классу астатических. Из уравнения (3) следует, что в астатической системе передаточная функция ошибки равна нулю в точке z=1, что выполняется, если передаточная функция разомкнутой системы в соответствии с (1) имеет полюс в этой же точке. (17)

Получение дискретной передаточной функции из непрерывной передаточной функции

Непрерывная часть цепи задана в обычном виде передаточной функцией W(s). Для отыскания дискретной передаточной функции W(z) необходимо предварительно находить весовую функцию из передаточной функции W(s), а затем воспользоваться выражением (6). К дискретной передаточной функции от непрерывной можно перейти через таблицы соответствия изображения по Лапласу и Z-изображения. Этому непосредственному переходу от W(s) к W(z) соответствует условная запись: (18)

Способы получения дискретной передаточной функции по формулам (2) и (18) являются точными, но их применение для реальных систем второго порядка и выше затруднительно. Поэтому в практических расчетах импульсных систем используют приближенные способы перехода от передаточной функции W(s) к дискретной передаточной функции W(z). Эти способы основаны на замене производной во времени, фигурирующей в уравнении непрерывной части, первой разностью: (19)

Запишем дифференциальное уравнение непрерывного интегратора: (20) и, подставив в него (19), получим разностное уравнение интегратора (21) Запишем уравнение (21) в Z-форме: (22) (23)

Учитывая, что обычная передаточная функция интегратора (24) получаем одну из наиболее часто используемых формул приближенного перехода от передаточной функции к дискретной передаточной функции: (25) Более точный переход от непрерывной системы к дискретной обеспечивает подстановка Тастина (26)

Частотные характеристики цифровых систем

Уравнения для частотных характеристик цифровых систем получаются из их передаточных функций путем замены оператора z на . Так как частота входит в показатель степени числа е , то частотные характеристики оказываются периодическими функциями частоты, период изменения которых равен T. Следовательно, нельзя различить составляющие, частоты которых кратны частоте работы дискретизатора .

Частотные характеристики цифровых САУ описываются трансцендентными уравнениями. Их определение связано со сложными расчетами, поэтому на практике вводят понятие псевдочастоты. Переход к псевдочастоте основан на введении комплексной переменной: (27) (28) Учитывая содержание z как и произведя замену , из (27) получим (29)

В выражении (29) введем обозначение (30) Теперь (29) принимает вид (31) Удобство псевдочастоты заключается в том, что на частотах, на которых выполняется условие T

Нетрудно убедиться, что при изменении частоты псевдочастота принимает значения от - до +, а комплексная переменная w движется по мнимой оси от -j до +j, то есть внутренняя часть круга единичного радиуса на плоскости комплексной переменной z отображается на левую полуплоскость комплексной переменной s. Таким образом, частотные характеристики цифровых САУ определяются уравнением: при

Контрольные вопросы

Какую информацию о системе управления нужно иметь для вычисления ее дискретной передаточной функции? Что называют импульсным фильтром? Как определяется дискретная передаточная функция системы при последовательном, параллельном соединении звеньев и соединении звеньев с обратной связью? Какие виды частотных характеристик используют для анализа цифровых систем? Для чего введено понятие псевдочастоты?

Рекомендуемая литература

Кривошеев В.П. Основы теории управления: Конспект лекций. Часть 2.  Владивосток: Изд-во ВГУЭиС, 1999. – 83 с. Лукас В.А. Теория автоматического управления. – М.: Недра, 1990. – 416 с.

Использование материалов презентации Использование данной презентации, может осуществляться только при условии соблюдения требований законов РФ об авторском праве и интеллектуальной собственности, а также с учетом требований настоящего Заявления. Презентация является собственностью авторов. Разрешается распечатывать копию любой части презентации для личного некоммерческого использования, однако не допускается распечатывать какую-либо часть презентации с любой иной целью или по каким-либо причинам вносить изменения в любую часть презентации. Использование любой части презентации в другом произведении, как в печатной, электронной, так и иной форме, а также использование любой части презентации в другой презентации посредством ссылки или иным образом допускается только после получения письменного согласия авторов.