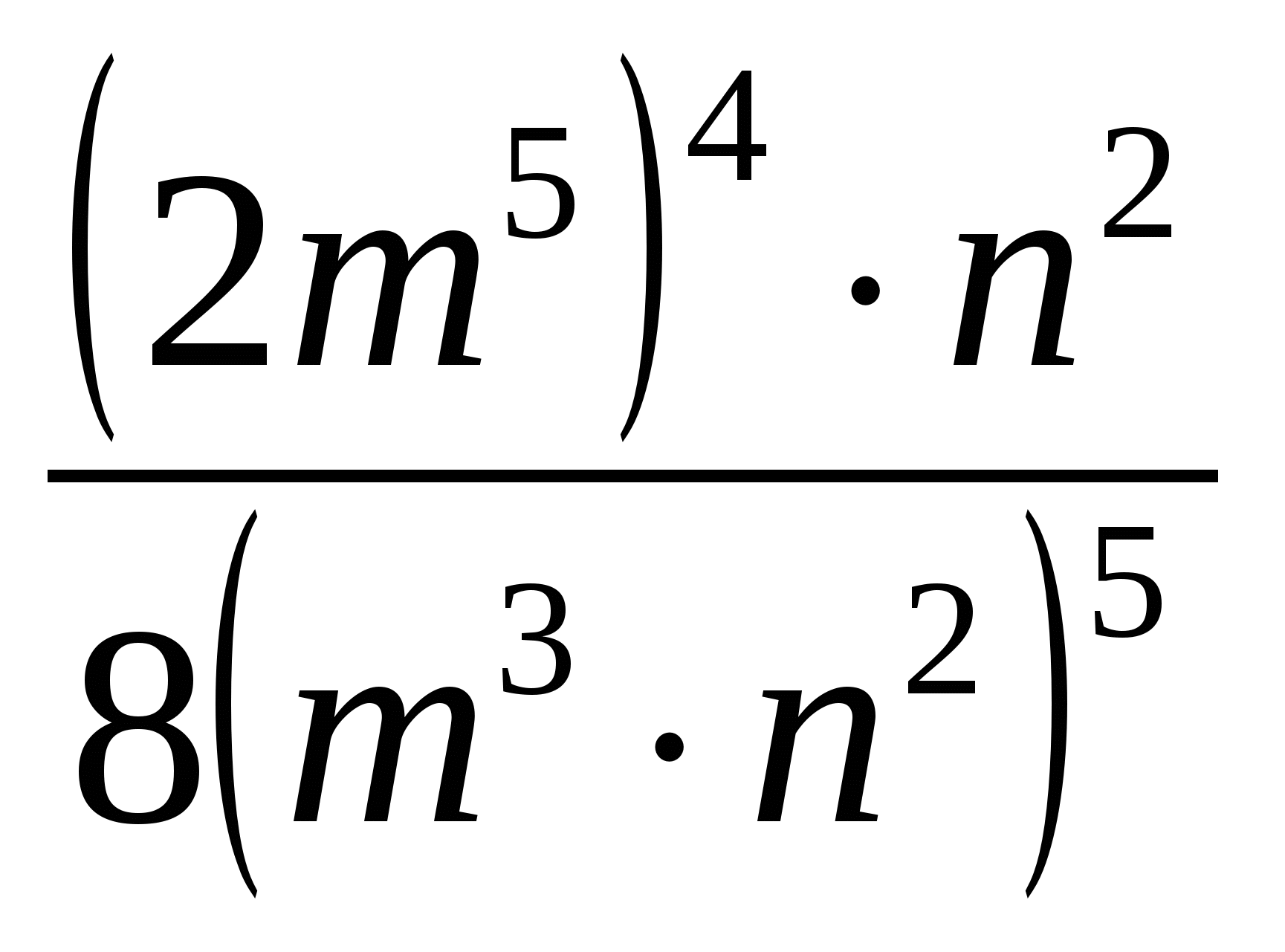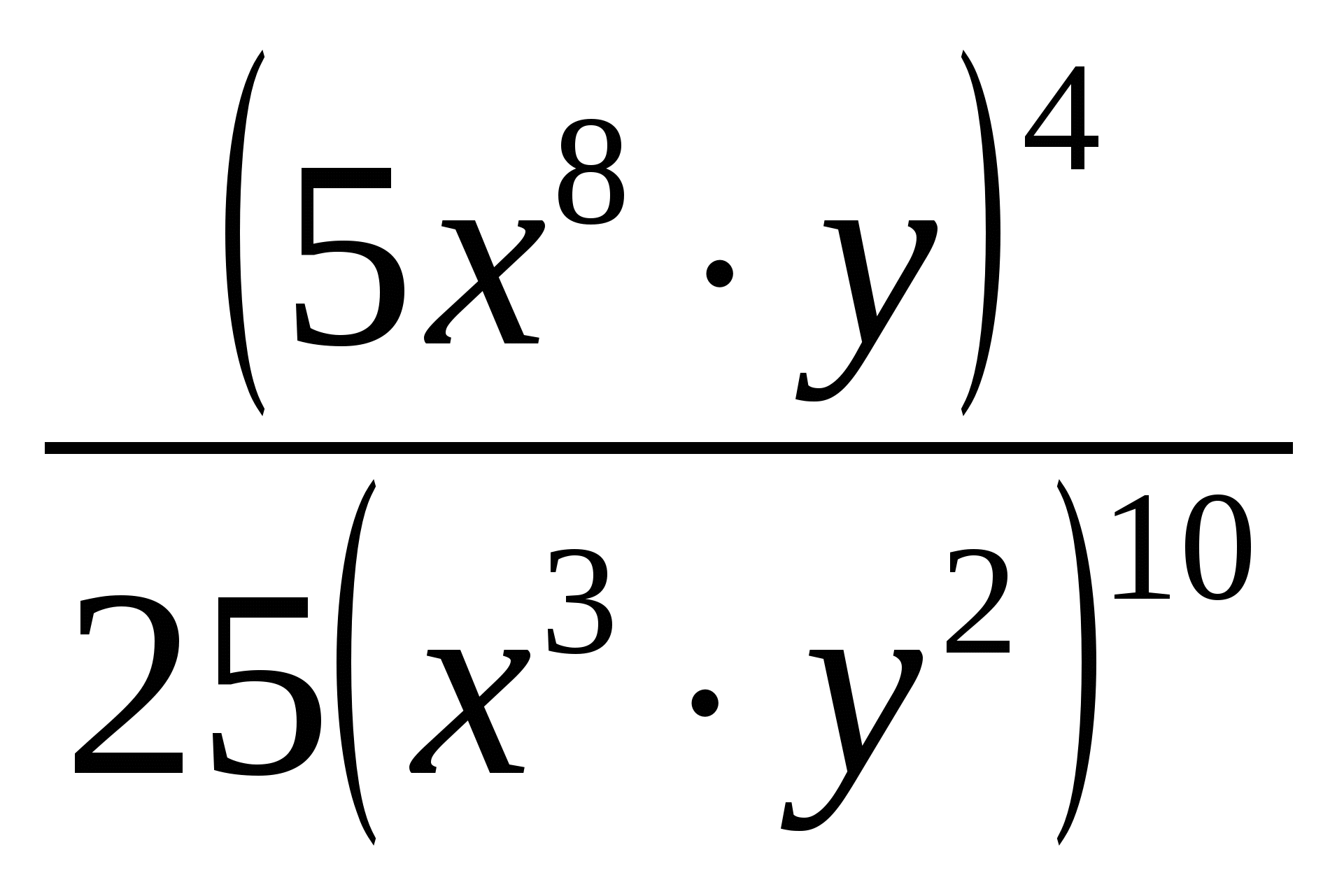Конспект урока «Обыкновенные и десятичные дроби 7 Класс» по математике для 7 класса
Урок 1. Обыкновенные и десятичные дроби.
Тема: Обыкновенные и десятичные дроби.
Цели урока: вспомнить и повторить правила выполнения действий с десятичными и обыкновенными дробями; в течение урока развивать у учащихся навыки решения примеров с обыкновенными и десятичными дробями, а так же вычислительные способности; рассказать об истории развития алгебры и ее ученых.
Ход урока:
1. Организационный момент. (3 мин.)
2. Вводная лекция. (5 мин.)
Алгебра, вместе с Арифметикой, есть наука о числах и через посредство чисел - о величинах вообще. Не занимаясь изучением свойств каких-нибудь определенных, конкретных величин, обе эти науки исследуют свойства отвлеченных величин, как таковых, независимо от того, к каким конкретным приложениям они способны. Различие между арифметикой и алгеброй состоит в том, что первая наука исследует свойства данных, определенных величин, между тем как алгебра занимается изучением общих величин, значение которых может быть произвольное, а, следовательно, алгебра изучает только те свойства величин, которые общи всем величинам, независимо от их значений. Таким образом, алгебра есть обобщенная арифметика. Это подало повод Ньютону назвать свой трактат об алгебре "Общею Арифметикой". Гамильтон, полагая, что подобно тому, как геометрия изучает свойства пространства, алгебра изучает свойства времени, назвал алгебру "Наукою чистого времени" - название, которое Деморган предлагал изменить в "Исчисление последовательности". Однако такие определения не выражают ни существенных свойств алгебры, ни исторического ее развития. Алгебру можно определить как "науку о количественных соотношениях". Развивали алгебру великие люди, про жизнь некоторых из них можно приготовить доклады.
АРХИМЕД (около 287-212 до нашей эры)
Архимед получил блестящее образование у своего отца, астронома и математика Фидия, родственника сиракузского тирана Гиерона II, покровительствовавшего Архимеду. В юности провел несколько лет в крупнейшем культурном центре того времени Александрии, где познакомился с Эрастосфеном. Затем до конца жизни жил в Сиракузах. Во время 2-й Пунической войны Архимед организовал инженерную оборону города. Изобретенные им военные метательные и др. машины (о них рассказывает Плутарх в жизнеописании римского полководца Марцелла) в течение двух лет сдерживали осаду Сиракуз римлянами. Архимеду приписывается также сожжение римского флота направленным на него через систему вогнутых зеркал солнечным светом, но это вряд ли достоверно. Гений Архимеда вызывал такое восхищение у римлян, что Марцелл приказал сохранить ему жизнь, но при взятии Сиракуз он был убит не узнавшим его солдатом.
Лекция о введении алгебры. Преподаватель должен рассказать о задачах алгебры и ее ученых. Так же надо рассказать о связи алгебры и других предметов.
3. Устный счет. (7 мин.)
Устный счет поможет вспомнить правила выполнения действий и развить вычислительные способности.
Цепочки с действиями обыкновенных дробей выполняются по действиям, вслух учениками произносится только ответ, причем только один раз. Каждое действие выполняют разные ученики.
![]()
![]()
Цепочка с десятичными дробями записана на плакате или на доске. Она так же выполняется по действиям. Подставить в эту цепочку можно числа 2,3; 0,7; 1,1.

4. Новый материал. (10 мин.)
Провести фронтальный опрос всего класса. Этот опрос поможет вспомнить все возможное о дробях.
Как называются члены дроби и что они означают?
Какую дробь называют правильной? Неправильной?
Расскажите правила перевода неправильной дроби в смешанное число.
Расскажите основное свойство дроби.
Что значит сократить дробь?
Как найти дробь от числа?
Расскажите понятие десятичной дроби.
Какое свойство десятичных дробей вы знаете?
Как перевести десятичную дробь в обыкновенную?
Любую ли обыкновенную дробь можно перевести в десятичную?
Если ученики не могут вспомнить ответ на какой-либо вопрос, учитель сам отвечает на него и объяснение происходит на доске. Если это, возможно, показывается пример, отвечающий на вопрос.
Устно, с полным объяснением разбираются примеры:
№ 1(а), 2(а, б), 4.
5. Закрепление материала. (15 мин.)
Затем на доске и в тетрадях выполняются № 1(б), 2(в). К доске вызываются сразу три ученика, каждый из них выполняет по три примера, а заем объясняет их. После того, как вспомнили все о дробях, класс приступает к решению примеров с дробями.
Решаются задания № 6, 7, 10, 34. Для экономии времени на доске выполняются одновременно по 3 – 4 примера (сколько позволяет доска).
6. Подведение итогов. (3 мин.)
7. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 1.1.
Решить и разобрать задания № 3, 8, 12.
Урок 2. Обыкновенные и десятичные дроби
Тема: Обыкновенные и десятичные дроби.
Цели урока: вспомнить и повторить правила сравнения обыкновенных и десятичных дробей; в течение урока развивать у учащихся навыки решения примеров с обыкновенными и десятичными дробями, сравнения дробей, а так же вычислительные способности.
Ход урока:
1. Организационный момент. (2 мин.)
2. Устный счет. (8 мин.)
На устный счет даются примеры – цепочки на десятичные дроби.
| 5,1 – 4,74 : 4 + 1,01 ∙ 3 + 0,07 = 3,37 | 10,2 : 3 + 1,1 : 0,9 - 1,5 ∙ 0,2 = 0,7 |
Так же устно разбираются примеры для развития вычислительной техники № 15, 16, 17.
3. Актуализация знаний. (15 мин.)
Чтобы вспомнить и закрепить правила решения примеров с дробями на доске с полным объяснением решаются примеры:
№ 11, 13.
4. Новый материал. (6 мин.)
Вспомнить правила сравнения десятичных дробей.
Устно выполнить сравнение № 19.
Вспомнить правила сравнения обыкновенных дробей.
Устно сравнить дроби:
![]() и
и ![]()
![]() и
и ![]()
![]() и
и ![]()
(Данные примеры можно приготовить на карточках или написать на доске.)
5. Закрепление материала. (10 мин.)
Решить и разобрать задания № 29, 21.
6. Подведение итогов. (2 мин.)
7. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 1.1.
Решить и разобрать задания № 9, 20, 31.
Урок 3. Обыкновенные и десятичные дроби
Тема: Обыкновенные и десятичные дроби.
Цели урока: вспомнить и повторить формулу, связывающую скорость, время и расстояние; показать правила решения и оформления задач на данную формулу; в течение урока развивать у учащихся умение решать задачи и вычислительные способности; проверить умение учеников решать примеры с обыкновенными и десятичными дробями.
Ход урока:
1. Организационный момент. (2 мин.)
2. Устный счет. (4 мин.)
На устный счет даются примеры – цепочки.
![]()
![]()
![]()
3. Новый материал. (4 мин.)
Вспомнить и записать на доске формулу ![]() и все формулы, вытекающие из нее.
и все формулы, вытекающие из нее.
Затем с помощью нее решить устно задачи.
Машина едет со скорость 80 км/ч. Сколько километров она проедет за 3 часа? За 10 часов? За 30 минут?
Велосипедист едет со скоростью 30 км/ч. Сколько времени ему потребуется, чтобы проехать 180 км? 300 км? 10 км?
№ 24 из учебника.
4. Закрепление материала. (21 мин.)
Решить и разобрать задания № 26, 39, 30, 32, 36.
5. Самостоятельная работа. (10 мин.)
| Вариант 2. | |
| № 40(а, г) | № 40(б, в) |
6. Подведение итогов. (2 мин.)
7. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 1.1.
Решить задания № 14, 22, 23, 28.
Урок 4. Степень с натуральным показателем
Тема: Степень с натуральным показателем.
Цели урока: объяснить понятие степени и правила вычисления степени с натуральным показателем; в течение урока развивать у учащихся навыки вычисления степеней и решения примеров с использованием степени; рассмотреть задания повышенной трудности с использованием степени.
Ход урока:
1. Организационный момент. (2 мин.)
2. Анализ самостоятельной работы. (5 мин.)
Выставить оценки за самостоятельную работу. Если в самостоятельной работе были повторяющиеся ошибки, разобрать их. Для закрепления данной темы, решить пример. На доске пример решается по действиям (разные действия – разные ученики).
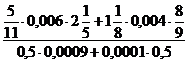
3. Новый материал. (8 мин.)
Дать определение степени.
С помощью определения, ученики должны найти верное равенство и объяснить ответ.
![]()
![]()
![]()
![]()
Также устно, с полным объяснением, вычислить: ![]()
4. Закрепление материала. (25 мин.)
Решить № 43, 45 (на доске записываются только ответы),
44 (устно), 48, 64.
На доске рассмотреть пример по записи степени. Объяснить данную запись и смысл данного выражения.
![]()
Тут же предложить учащимся представить данную степень в виде произведения двух других степеней с основанием 4.
После решить № 55, 56, 57 (устно).
5. Подведение итогов. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 1.2.
Решить задания № 47, 58, 42.
Урок 5. Степень с натуральным показателем
Тема: Степень с натуральным показателем.
Цели урока: объяснить правила возведения в степень отрицательных чисел; в течение урока развивать у учащихся навыки вычисления степеней и решения примеров с использованием степени; показать правила нахождения последней цифры результата, не выполняя вычислений.
Ход урока:
1. Организационный момент. (2 мин.)
2. Индивидуальный опрос. (4 мин.)
Двое учеников вызываются к доске, на которой заранее записаны задания по упрощению выражений:
| Карточка 2.
|
Пока двое учеников выполняют задание, остальные устно вычисляют:
![]()
После проверяются примеры на доске.
3. Актуализация знаний. (5 мин.)
Для закрепления понятия степени решаются примеры № 49.
4. Новый материал. (7 мин.)
Устно выполняется № 51. А на доске еще остались примеры из № 49. По этим двум номерам разбирается, что происходит с отрицательными числами в четной степени и в нечетной степени. Так же разбирается, почему четная степень делает число положительным, а нечетная степень отрицательное число оставляет отрицательным.
5. Закрепление материала. (22 мин.)
Для закрепления материала устно, с полным объяснением, разбирается № 50.
После выполняются на доске и в тетрадях задания
№ 52, 65, 66, 67, 59, 60, 72.
Разобрать следующее задание:
Не вычисляя выражения, найти цифру, на которую заканчивается результат данного действия.
![]()
6. Подведение итогов. (3 мин.)
7. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 1.2.
Решить задания № 68, 53, 54, 71.
Урок 6. Решение задач на проценты
Тема: Решение задач на проценты.
Цели урока: в течение урока развивать у учащихся вычислительные способности с использованием степени; объяснить понятие процентов; вспомнить и повторить правила решения и оформления задач на проценты; рассмотреть задачи – шутки с процентами для повышения интереса к математике.
Ход урока:
1. Организационный момент. (2 мин.)
2. Устный счет. (4 мин.)
|
|
|
3. Новый материал. (12 мин.)
Вспомнить понятие и обозначение процентов, правила перевода десятичных дробей в проценты и обратно.
Вспомнить правила оформления и решения задач на проценты, решив следующую задачу.
Мама купила 2 кг. 400 г. конфет. Известно, что 30% всех конфет – шоколадные конфеты. Сколько шоколадных конфет купила мама?
Эта задача рассматривается на доске. И тут же из нее можно сделать и разобрать следующие задачи.
Мама купила 720 г. шоколадных конфет. Известно, что они составляют 30% всех конфет. Сколько килограмм конфет купила мама?
Мама купила 2 кг. 400 г. конфет. Известно, что из них 720 г. шоколадных конфет. Сколько процентов составляют шоколадные конфеты от общего количества?
4. Закрепление материала. (22 мин.)
Для закрепления материала устно, с полным объяснением, разбирается № 74, 75.
После выполняются на доске и в тетрадях задачи
№ 76, 79, 81, 83.
Затем № 86 выполняется по рядам. Первый ряд (а), второй ряд (б), третий ряд (в). Дается некоторое время на обдумывание, затем кто-то с ряда показывает решение на доске.
Рассмотреть решение следующих задач.
1) Малыш полетел к Карлесону в гости. Когда они пролетели 56 м, что составило 70% всего расстояния, моторчик заглох. Сколько метром еще им осталось пролететь до дома Карлесона?
2) В школе добросовестно учатся 430 учеников, а еще 70 валяют дурака. Какой процент учеников школы валяют дурака?
3) Коля и Толя закопали свои дневники, Коля на глубину 10 метров, а Толя – 12 метров. Археологи далекого будущего когда-нибудь раскопают оба окаменевших дневника с большим количеством окаменевших двоек. В Колином дневнике они найдут 224 двойки, а в Толином 25% этих двоек. Сколько всего двоек найдут археологи в окаменевших дневниках?
5. Подведение итогов. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 1.3.
Решить задания № 68, 53, 54, 71.
Урок 7. Решение задач на проценты
Тема: Решение задач на проценты.
Цели урока: проверить знания и умения по работе с процентами, степенями и дробями; в течение урока развивать у учащихся вычислительные способности с использованием степени, дробей и процентов; так же развивать у учеников навыки решения и оформления задач на проценты; рассмотреть задачи – шутки с процентами для повышения интереса к математике.
Ход урока:
1. Организационный момент. (2 мин.)
2. Математический диктант. (8 мин.)
| Вариант 2. | |
| 1) Перевести десятичные дроби в проценты. | |
| 0,2; 0,03; 1,14. | 0,68; 0,002; 0,9. |
| 2) Перевести проценты в десятичные дроби. | |
| 38%, 0,3%, 50%. | 120%, 1%, 70%. |
| 3) Вычислить. | |
|
|
|
| 4) Найти 20% от 35. | 4) Найти число, если его 20% - 12. |
Ученики меняются тетрадями и под диктовку учителя проверяют ответы и ставят оценки. После разбираются ошибки.
3. Устная работа. (10 мин.)
Затем устно разбираются № 78, 87, 88, 85.
4. Решение задач. (10 мин.)
Решаются на доске № 92, 94.
Также решить следующую задачу:
40 бабушек вошли в автобус. 70% бабушек купили билеты, а остальные закричали, что у них проездной билет. Контролер проверил. На самом деле оказалось, что проездной только у 7 бабушек. Сколько бабушек ехало «зайцами»?
5. Самостоятельная работа. (10 мин.)
| Вариант 2. | |
| Вычислить значение выражения: | |
|
|
|
| Задача № 89 | Задача № 90 |
6. Подведение итогов. (3 мин.)
7. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 1.3.
Решить задания № 84, 91, 93.
Урок 8. Решение задач на проценты
Тема: Решение задач на проценты.
Цели урока: проверить умение учеников решать задачи на проценты и решать примеры с дробями; в течение урока развивать у учащихся навык решения и оформления задач на проценты; рассмотреть задачи – шутки с процентами для повышения интереса к математике.
Ход урока:
1. Организационный момент. (2 мин.)
2. Анализ самостоятельной работы. (3 мин.)
Выставить оценки за самостоятельную работу. Если какие-то ошибки повторялись, то их разобрать на доске.
3. Индивидуальный опрос. (12 мин.)
Из тех учеников, кто плохо написал самостоятельную работу, вызвать к доске четырех человек, на работу с карточкой. А остальные в этот момент решают в тетрадях № 97.
| Карточка 2. Мальчик прочитал 40 страниц книги, что составило 25% объема книги. Сколько страниц в книге? |
| Карточка 3. В трех ящиках – 240 кг свеклы. В первом ящике – 25% всей свеклы, а во втором – 80% оставшейся после того, как заполнили первый ящик. Все остальное сложили в третий ящик. Сколько свеклы в третьем ящике? |
| Карточка 4. Скорость легковой машины 96 км/ч, что составляет 12% скорости самолета. Какова скорость самолета? |
На решение дается 5 – 7 минут, после чего проверяются задачи, решенные на доске, а затем проверяется устно № 97.
4. Решение задач. (17 мин.)
Решение задач на проценты из второй главы можно провести следующим образом. На доске выписать номера, а ученики в тетрадях решают задачи из данных на выбор. После 10 минут решения, к доске вызвать пятерых учеников (если доска не позволяет, сначала троих, а затем еще двоих), которые решили соответствующие задачи. На запись дается 3 – 5 минут, после чего каждый объясняет свою задачу (и получает оценку). Преподаватель может в этот момент взять тетради у тех, кто за это время решил 2 или 3 задачи, и выставить им оценки. Сидящие проверяют свои записи и дополняют их.
Решить № 101, 102, 104, 106, 107.
Если осталось время, совместными усилиями класса разобрать решение задачи:
Хор, состоящий из 280 мальчиков и 105 девочек, исполняет задушевную песню. К счастью, лишь 25% мальчиков и третья часть девочек орет во все горло, а остальные только открывают рот. Сколько процентов составляют орущие девочки от орущих мальчиков?
5. Закрепление – тестирование. (6 мин.)
Для закрепления пройденного материала и проверки усвоенного тестирование из трех заданий. Записать можно на доске. Каждый выполняет самостоятельно в тетради. После 6 минут решения проверяются ответы, если какое-то задание не выполнили большинство учеников, то это задание разбирается на доске.
1. Найти произведение чисел, обратных к числам ![]() и
и ![]() .
.
1) ![]() 2) 1; 3)
2) 1; 3) ![]() 4) 2; 5)
4) 2; 5) ![]()
2. Чему равно значение выражения ![]() ?
?
1) 1; 2) 1,6; 3) ![]() 4) 0,6; 5)
4) 0,6; 5) ![]()
3. В аудитории, где проходит экзамен, 56% - девочки, остальные мальчики. Среди приведенных чисел выберете то, которое может быть числом абитуриентов в этой аудитории.
1) 44; 2) 60; 3) 80; 4) 99; 5) 50.
ОТВЕТЫ: 1 – 1, 2 – 5, 3 – 5.
6. Подведение итогов. (3 мин.)
7. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 1.3.
Решить задания № 100, 105, 95.
Урок 9. Статистические характеристики
Тема: Статистические характеристики.
Цели урока: объяснить понятие ряда; ввести понятия среднего арифметического, размаха и моды ряда; рассказать о науке – статистике и ее применении в жизни; рассмотреть наглядное применение статистики в повседневной жизни. В течение урока развивать у учащихся навык нахождения статистических характеристик, умение обучаться самостоятельно. А так же в течение урока воспитывать в детях чувство сотрудничества.
Ход урока:
1. Организационный момент. (2 мин.)
Для изучения данной темы требуется возможность обсуждения, поэтому урок проводится в групповой форме. Учеников рассадить в группы по 5 человек.
2. Новый материал. (13 мин.)
Статистика – наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в природе и обществе. Слово «статистика» происходит от латинского слова ![]() , которое означает «состояние, положение вещей». Статистика изучает численность отдельных групп населения страны и ее регионов, производство и потребление разнообразных видов продукции, перевозку грузов и пассажиров различными видами транспорта, природные ресурсы и многое другое. Результаты статистических исследований широко используются для практических и научных выводов. В настоящее время статистика начинает изучаться уже в средней школе, в ВУЗах это обязательный предмет, потому что связан со многими науками и отраслями. Чтобы увеличить количество продаж в магазине, чтобы улучшить качество знаний в школе, чтобы двигать страну по экономическому росту, надо проводить статистические исследования и делать соответствующие выводы. И это должен уметь каждый.
, которое означает «состояние, положение вещей». Статистика изучает численность отдельных групп населения страны и ее регионов, производство и потребление разнообразных видов продукции, перевозку грузов и пассажиров различными видами транспорта, природные ресурсы и многое другое. Результаты статистических исследований широко используются для практических и научных выводов. В настоящее время статистика начинает изучаться уже в средней школе, в ВУЗах это обязательный предмет, потому что связан со многими науками и отраслями. Чтобы увеличить количество продаж в магазине, чтобы улучшить качество знаний в школе, чтобы двигать страну по экономическому росту, надо проводить статистические исследования и делать соответствующие выводы. И это должен уметь каждый.
Затем надо прочитать задачу и опросить учеников, что они могут сказать и какие выводы сделать. Для начала дать группам самостоятельно это обсудить, а затем выслушать нескольких человек и обсудить услышанное.
В институте сдавали зачет по высшей математике. В группе было 10 человек, и они получили соответствующие оценки:
3, 5, 5, 4, 4, 4, 3, 2, 4, 5.
Можно задать следующие вопросы.
Какую оценку получали чаще всего?
Как в целом сдала группа?
Насколько разные были оценки?
После обсуждения с учениками, дать время на прочтение параграфа данной темы. Ученики должны в группе прочесть данный материал и ввести понятие ряда и характеристик ряда. Дать определения статистическим характеристикам ряда, объяснить их значение и вычислить их для данного ряда. Затем сверяются ответы и если что-то ученики поняли или вычислили не верно, то преподаватель исправляет и объясняет.
3. Закрепление нового материала. (10 мин.)
Для закрепления устно выполнить № 111.
Затем для каждой группы на карточках раздать ряд чисел, для которого надо найти среднее арифметическое, размах ряда и моду.
| Карточка 2. |
| Карточка 3. |
| Карточка 4. |
| Карточка 5. |
С каждой группы по одному ученику должны показать решение своего задания у доски и объяснить его всему классу. Письменно всеми учениками решаются задания № 118, 119, объяснение решения и оформления должны быть на доске.
4. Статистическое исследование. (15 мин.)
Затем предложить ученикам каждой группы провести исследование, оно у всех групп одинаковое, но оформить лучше на карточках.
В женском обувном магазине провели статистические исследования и составили соответствующую таблицу по цене обуви и количества продаж:
| 500 | 1200 | 1500 | 1800 | 2000 | 2500 | |
| Количество | 8 | 9 | 14 | 15 | 3 | 1 |
Для данных показателей надо найти статистические характеристики и объяснить их значение. После ученики должны ответить на следующие вопросы:
Из данных ценовых категорий, обувь за какую цену не следует продавать магазину?
Обувь, по какой цене следует распространять?
К какой цене лучше стремиться?
По каким параметрам еще можно провести статистические исследования в обувном магазине?
Приведите еще наглядные примеры использования статистики.
5. Подведение итогов. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 1.4.
Решить задания № 110, 114, 116, 108.
Урок 10. Статистические характеристики
Тема: Статистические характеристики.
Цели урока: объяснить правила построения столбчатых и круговых диаграмм; рассмотреть решение задач по статистике повышенной трудности; проверить умение находить статистические характеристики. В течение урока развивать у учащихся навык нахождения статистических характеристик и умение строить диаграммы различных видов.
Ход урока:
1. Организационный момент. (2 мин.)
2. Индивидуальный опрос. (10 мин.)
К доске вызвать трех учеников, для работы по карточкам.
| Карточка 2. Участник соревнований по стрельбе сделал 10 выстрелов, получая за каждый выстрел балл из 10 возможных баллов, получили следующий ряд данных: 7, 7, 9, 8, 6, 4, 10, 9, 9, 10. Найдите для этого ряда среднее арифметическое, размах ряда и моду. Что характеризует каждый из этих показателей? |
| Карточка 3. Участник соревнований по стрельбе сделал 10 выстрелов, получая за каждый выстрел балл из 10 возможных баллов, получили следующий ряд данных: 6, 7, 9, 8, 6, 7, 8, 8, 9, 8. Найдите для этого ряда среднее арифметическое, размах ряда и моду. Что характеризует каждый из этих показателей? |
Остальные в этот момент решают в тетрадях задание № 121.
На решение дается 5 минут, после чего проверяются задачи на доске. После проверки задач ученики сравнивают результаты участников из 2-ой и 3-ей карточек, выясняя, кто из участников победил и по какой характеристике лучше судить соревнования. Затем проверяется устно задание № 121.
3. Новый материал. (10 мин.)
После работы с диаграммой из задания № 121, обсудить правила построения столбчатой диаграммы и построить совместными усилиями на доске и в тетрадях диаграмму по условию задачи.
В течении двух кварталов отмечалось посещение бассейна по месяцам: январь – 685 человек, февраль – 790 человек, март – 1005 человек, апрель – 1560 человек, май – 1000 человек, июнь – 2545.
Затем объяснить правила построения круговой диаграммы и построить на доске такого вида диаграмму по условию задачи.
В классе 36 человек, из них 20 человек – хорошисты, 5 – отличники, а остальные троечники.
Сравнить два вида диаграмм, и обсудить когда и какого вида диаграммы применяются.
4. Решение задач. (18 мин.)
Решить задачи – исследования и сделать соответствующие выводы по заданиям № 122, 123, 124.
Так же разобрать следующие задачи:
1) В ряду чисел 3,8,15,30,_,24 пропущено одно число. Найдите его, если среднее арифметическое ряда равно 20; если размах ряда равен 30; мода ряда равна 8.
2) Относительно трех чисел известно, что среднее арифметическое первых двух равно 25, а среднее арифметическое всех трех чисел – 30. Чему равно третье число?
3) Задачи № 120, 115.
5. Подведение итогов. (3 мин.)
6. Домашнее задание. (2 мин.)
Ответить на вопросы для повторения к главе, письменно ответить на вопросы 3, 4, 5, 6.
Решить задание № 119 (построить два вида диаграмм).
Урок 11. Подготовка к контрольной работе
Тема: Подготовка к контрольной работе.
Цели урока: повторить и закрепить понятия степени, процентов, определения статистических характеристик; подготовиться к контрольной работе; проверить готовность к контрольной работе. В течение урока развивать у учащихся навык решения задания по пройденным темам.
Ход урока:
1. Организационный момент. (2 мин.)
Рассадить детей на 4 группы. Рассказать тему и цели урока.
2. Актуализация знаний. (8 мин.)
В группах письменно отвечают на вопросы из заданий для самопроверки: 1, 2, 3, 4, 5, 8, 10, 11. Решение должно быть у каждого в тетради, и каждый должен знать объяснение заданий. На выполнение дается 7 минут. После чего все задания проверяются устно, при этом отвечающие должны ответить на следующие вопросы:
Как переводить десятичную дробь в обыкновенную?
Как переводить обыкновенную дробь в десятичную?
Любую ли дробь можно перевести в десятичную?
Расскажите алгоритм сравнения обыкновенных дробей.
Как сравнить десятичные дроби?
Что значит порядок возрастания? Убывания?
Расскажите понятие степени с натуральным показателем.
Как перевести десятичную дробь в проценты?
Как проценты представить десятичной дробью?
3. Закрепление материала. (10 мин.)
Каждой группе раздается карточка, задания которой выполняют в группе совместно. Затем по ответам, соответствующим ответам буквам и номеру задания составляется на доске фраза. Должно получиться «Математика – царица наук». Если какая-либо буква найдена не верно и фраза не составляется, то задание под этим номером рассматривается на доске всем классом.
| Карточка 2. 1) Какое из чисел меньше 0,094 или 3) 6) 10) В спортивной секции волейболом занимается 54 человека. Сколько членов в этой секции, если известно, что волейболом занимается 75% всей секции? 17) Найдите размах ряда 14, 18, 14, 20, 19, 14. |
| Карточка 3. 4) 13) Какое из чисел меньше 14) Известно, что в журналах 24% рекламы. Сколько всего страниц в журнале, если Катя насчитала 36 страниц рекламы. 15) 16) Найдите моду ряда 70, 72, 62, 72, 80, 70, 72. |
| Карточка 4. 8) 20) 19) Найдите среднее арифметическое чисел 21, 24, 21, 23, 21. 9) Какое из чисел больше 12) Оля прочитала 30% всей книги. Сколько страниц прочитала Оля, если в книге 240 страниц. |
| И – 150 | Ц – 361 | У – 22 | Т – 0,105 | |
| А – 72 | Н – 6 | Е – | К – 2,57 | Р – |
4. Проверка – тестирование. (6 мин.)
Тесты можно оформить на карточках, для каждой группы по одной. Решать данные задания ученики должны самостоятельно. Решение проверяется по ответам. Если у нескольких учеников вызвало затруднение какое-нибудь задание, оно разбирается на доске и дается время на обсуждение его в группе.
1. Вычислите ![]() .
.
1) 6,84; 2) 5,82; 3) – 6,84; 4) – 5,82; 5) 5,84.
2. В 140 грамм воды добавили 60 г соли. Сколько процентов соли в этом соленом растворе?
1) 20; 2) 30; 3) 25; 4) 35; 5) 45.
3. Среднее арифметическое трех чисел равно 10, а среднее арифметическое двух других 15. Найдите среднее арифметическое этих пяти чисел.
1) 10; 2) 11; 3) 12; 4) 13; 5) 14.
ОТВЕТЫ: 1 – 3, 2 – 2, 3 – 3.
5. Решение задач. (14 мин.)
Преподаватель объяснят решение и правила оформления задания № 129.
Затем дается каждой группе один из номеров задач № 125, 126, 127, 128 и на решение 5 минут. Те группы, которые справились со своей задачей, выдвигают одного из учеников для объяснения задачи на доске. Если какая-то группа не справилась с задачей, она дается им для домашнего решения. И во время анализа контрольной работы им дается возможность объяснить и показать ее решение. Если же ученики и дома не справятся с задачей, то сам преподаватель объясняет ее решение.
6. Подведение итогов. (3 мин.)
7. Домашнее задание. (2 мин.)
Решить задания № 7, 9, 13, 15 (стр. 35 – 36), задачу №126.
Контрольная работа.
Цели урока: проверить знания учеников по данной теме.
Ход урока:
1. Организационный момент.
2. Контрольная работа.
Вариант 1.
1. Найти значения выражений:
а) ![]() б)
б) ![]() в)
в) ![]()
2. Сравнить числа:
а) ![]() и
и ![]() б)
б) ![]() и
и ![]() ; в)
; в) ![]() и
и ![]() .
.
3. Боря потратил 5% своих денег. Сколько было у Бори денег, если после того, как он их потратил, у него осталось 160 рублей?
4. На празднике 75% цветов были розы, а остальные 224 цветка – георгины. Сколько всего цветов было на празднике?
5. Найдите среднее арифметическое значение, моду и размах ряда:
15, 121, - 61, 121, 0, 20.
Вариант 2.
1. Найти значения выражений:
а) ![]() б)
б) ![]() в)
в) ![]()
2. Сравнить числа:
а) ![]() и
и ![]() б)
б) ![]() и
и ![]() ; в)
; в) ![]() и
и ![]() .
.
3. Количество деревьев в саду в мае выросло на 4%. Сколько деревьев стало в саду, если в апреле их было 650?
4. 65% шаров на празднике были красными. А остальные 175 – зелеными. Сколько всего шаров было на празднике?
5. Найдите среднее арифметическое значение, моду и размах ряда:
35, - 23, 121, - 55, 35, - 35.
3. Домашнее задание.
Решить задания № 130, 131.
Тема: Что такое отношение.
Цели урока: подвести итоги проведенной контрольной работы и провести работу над ошибками. Объяснить понятие отношения; показать правила записи и прочтения отношений. В течение урока развивать у учащихся навык нахождения отношений и решения задач на данную тему.
Ход урока:
1. Организационный момент. (2 мин.)
2. Анализ контрольной работы. (8 мин.)
Выставить оценки в журнал за контрольную работу в журнал. На доске решить и разобрать те задания, по которым было допущено больше всего ошибок. Так же для закрепления пройденного материала предлагается решить следующие задания:
1) Найти значение выражения: ![]() .
.
2) В начале года мальчики составляли 30% учеников класса, а девочек было 21. В середине года в класс пришли 6 мальчиков, а 6 девочек перешли в другой класс. Каким стал после этого процент мальчиков в классе?
3. Новый материал. (15 мин.)
Дать определение отношению и правило его прочтение. Для того, чтобы объяснить смысл отношения дать условие задачи «В классе 25 учеников. Из них 15 мальчиков и 10 девочек» и вместе с учениками ответить на следующие вопросы:
Какую часть класса составляют девочки?
Какую часть класса составляют мальчики?
Какую часть количество девочек составляет от числа мальчиков?
Во сколько раз мальчиков больше девочек?
Сколько процентов от всего класса составляет число девочек?
Сколько процентов от всего класса составляет количество мальчиков?
4. Закрепление нового материала. (15 мин.)
Разобрать на доске задания № 132, 134.
Затем устно решить задания № 135, 136, 137, 138.
И после этого письменно решаются номера № 140, 141, 142.
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 2.1.
Решить задания № 133, 139, 144, 145.
Задание № 145 дается домой по рядам. (1ый ряд – (а), 2ой ряд – (б), 3ий – (в))
Тема: Что такое отношение.
Цели урока: повторить и закрепить понятие отношения правила записи и прочтения отношений; рассмотреть задачу – шутку на нахождение отношения для повышения интереса к математике. В течение урока развивать у учащихся навык нахождения отношений и решения задач на данную тему. Проверить умение решать задачи на нахождения отношений.
Ход урока:
1. Организационный момент. (2 мин.)
2. Устная работа. (10 мин.)
На доске или на карточках написать отношения, которые учащиеся должны прочитать и по возможности устно сократить.
| 8 : 12 | 30 : 9 | 0,2 : 1,2 | |
| 3,3 : 2,2 | 7 : 70 |
|
|
Разобрать из домашнего задания задание № 145. С каждого ряда вызвать по одному ученику, который должен объяснить правила выполнения задания и результат.
3. Решение задач. (18 мин.)
На доске выполняются номера № 146, 148, 154, 156, 157.
Так же решить задачу:
Мишу за плохое поведение дома ругают папа, мама и бабушка. За неделю Миша насчитал маминых наказаний 8, папиных порок 5, и бабушкиных наставлений 7. Какую часть составляют папины порки от всех наказаний за неделю?
4. Самостоятельная работа. (10 мин.)
| Вариант 2. | |
| № 150, 152 | № 151, 153 |
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 2.1.
Решить задания № 147, 149, 155.
Урок 15. Что такое отношение
Тема: Что такое отношение.
Цели урока: повторить и закрепить понятие отношения правила записи и прочтения отношений; рассмотреть задачу – шутку на нахождение отношения для повышения интереса к математике. В течение урока развивать у учащихся навык нахождения отношений и решения задач на данную тему.
Ход урока:
1. Организационный момент. (2 мин.)
2. Анализ самостоятельной работы. (3 мин.)
Выставить оценки и на доске разобрать задачи, которые не решило большинство учеников.
3. Индивидуальный опрос. (15 мин.)
Три ученика вызываются к доске на решение задач по карточкам.
| Карточка 2. В бутылке 500 миллилитров лимонада. Выпили 260 мл. Какая часть лимонада осталась в бутылке. |
| Карточка 3. Смешали 20 г кофе и 60 г сахара. Какой процент смеси составляет кофе. |
В этот момент остальные ученики устно разбирают № 167.
После того этого проверяются задачи, решенные на доске.
4. Решение задач. (20 мин.)
Решаются № 169, 168, 170, 171, 163.
Так же решить задачу:
По литературе задали сочинить стихотворение о школе. В 5 «А» классе в стихотворной форме рассказали о вредности физкультурника 9 человек, о требовательности математички – 10 человек, о строгости учителя по географии – оставшиеся 6 учеников класса. Сколько процентов учеников класса жаловались на преподавателя физкультуры?
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 2.1.
Решить № 160, 162, 175.
Тема: Деление в отношении.
Цели урока: повторить и закрепить понятие отношения правила записи и прочтения отношений; объяснить правила деления чисел в заданном отношении; рассмотреть задачу – шутку на нахождение отношения для повышения интереса к математике. В течение урока развивать у учащихся навык нахождения отношений и деления чисел в заданном отношении.
Ход урока:
1. Организационный момент. (2 мин.)
2. Устный счет. (5 мин.)
На доске или на карточках написать отношения, которые ученики должны прочитать и вычислить.
![]()
Вспомнить определение отношения, и повторить, на какие вопросы помогает ответить отношение.
3. Новый материал. (8 мин.)
Рассказать о делении чисел в данном отношении, дать определение пропорциональным величинам. Рассмотреть вместе с учащимися задачу, дать возможность ученикам предложить ход решения.
Родительский комитет на поздравление детей собрал 1620 рублей. На 23 февраля надо поздравить 15 мальчиков, а на 8 марта – 12 девочек. Как разделить деньги?
Решая задачу, надо обратить внимание на правила оформления задач такого вида.
4. Закрепление нового материала. (20 мин.)
Решаются № 176, 180, 182, 183, 190.
Так же предлагается решить задачу – шутку:
У Оли, Светы и Даши было всего 28 цветных карандашей. Чтобы поделить их между собой девочки устроили жестокую драку, в результате которой карандаши разделили в отношении 2: 2: 3. Известно, что больше всего карандашей отвоевала себе Даша. Сколько карандашей у Даши?
Затем по рядам для самостоятельного решения дается № 192. Решение задач проверяется устно.
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 2.2.
Решить № 177, 181, 182.
Урок 17. Деление в отношении
Тема: Деление в отношении.
Цели урока: повторить и закрепить понятие отношения правила записи и прочтения отношений, правила деления чисел в заданном отношении; рассмотреть задачу – шутку на нахождение отношения для повышения интереса к математике; проверить умение решать задачи на делении чисел в заданном отношении. В течение урока развивать у учащихся навык нахождения отношений и деления чисел в заданном отношении.
Ход урока:
1. Организационный момент. (2 мин.)
2. Устный счет. (8 мин.)
Устно рассмотреть и обсудить решение заданий № 184, 185, 187.
Закрепить понятие деления числа в данном отношении и разложить устно число 60 в данном отношении.
4 : 2; 1 : 5; 2 : 3; 1 : 9; 1 : 2.
3. Решение задач. (15 мин.)
Вспомнить определение отношения, правила его вычисления и упрощения, решить задание №188.
Затем разобрать задачи № 190, 193, а так же следующие задачи:
1) Вася за неделю получил 18 двоек, даже мама удивилась, просматривая дневник. Двойки Вася получил по математике, истории и литературе в отношении 3: 2: 4 соответственно. Сколько двоек по математике получил Вася за неделю?
2) Число 459 представили в виде суммы трех слагаемых, которые относятся, как 1: 2: 6. Найдите разность между большим и меньшим слагаемыми.
После чего дать детям творчески поработать: придумать задачу на деление числа в данном отношении. Несколько задач разобрать.
4. Самостоятельная работа. (15 мин.)
| Вариант 2. | |
| № 178, 186(а, в) | № 179, 186(б, г) |
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 2.2.
Решить задания № 189, 191, 174.
Урок 18. Пропорции
Тема: Пропорции.
Цели урока: объяснить понятие пропорции, ее крайних и средних членов; рассказать правила прочтения и записи пропорции; показать правила составления пропорций из заданных чисел. В течение урока развивать у учащихся навык чтения и записи пропорций, проверки верности пропорций, а также развивать умение самостоятельно делать выводы.
Ход урока:
1. Организационный момент. (2 мин.)
2. Анализ самостоятельной работы. (3 мин.)
Выставить оценки. Рассмотреть на доске задачи, в решении которых было допущено наибольшее количество ошибок.
3. Устный счет. (8 мин.)
Прочитать и вычислить данные отношения.
15 : 5; 10 : 20; 0,6 : 3; 0,9 : 0,3; ![]()
![]()
Прочитать отношения, равные между собой.
4. Новый материал. (10 мин.)
Из устного счета на доку записать верные отношения. На их примере дать определение пропорции, выделить крайние и средние члены пропорции и рассказать правила прочтения пропорций. Записать пропорции из номера № 196. Разобрать устно задание № 195. Затем вместе с учениками устно найти в каждой из данных в этом номере пропорций произведение крайних членов и произведение средних членов пропорции. Найти закономерность и сформулировать основное свойство пропорций.
5. Закрепление нового материала. (17 мин.)
Разобрать задания № 198, 199 (для экономии времени по рядам).
После этого выполнить задание № 212 и на его основе № 211.
Затем предлагается решить следующую задачу:
Разделить прямоугольник со сторонами 6 см и 4 см на два прямоугольника таким образом, чтобы их площади выражались натуральными числами и их отношение было равно отношению 1: 2. Покажите рисунок. Сколькими способами можно провести соответствующее деление?
Также проверить верной или нет является данная пропорция
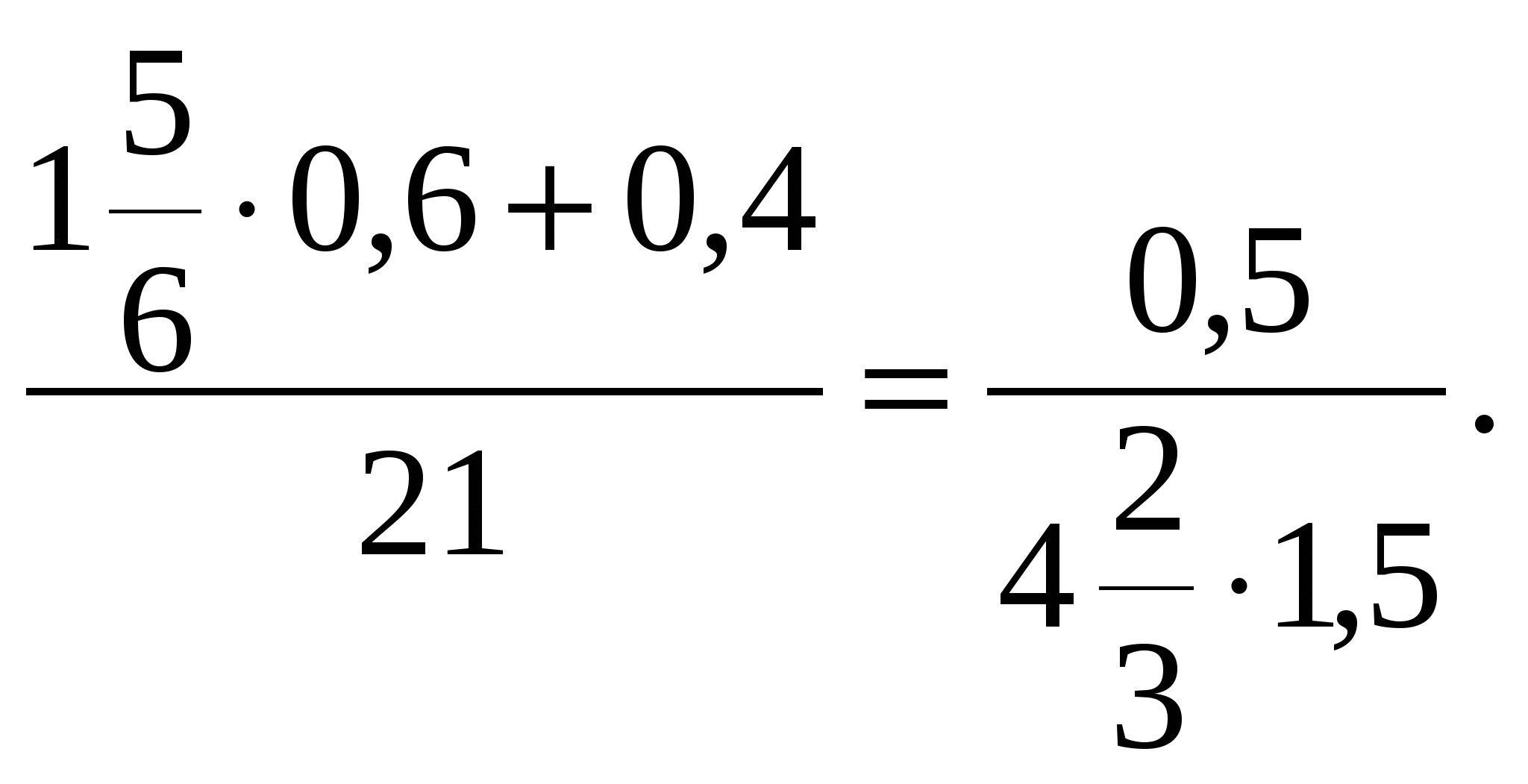
6. Итоги урока. (3 мин.)
7. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 2.3.
Решить задания № 197, 210, 214(а).
Урок 19. Пропорции
Тема: Пропорции.
Цели урока: повторить и закрепить понятие пропорции, ее крайних и средних членов, основное свойство пропорции; объяснить правила нахождения неизвестных членов пропорции; показать правила решения уравнений и задач на пропорции. В течение урока развивать у учащихся навык решения уравнений и задач на пропорцию.
Ход урока:
1. Организационный момент. (2 мин.)
2. Актуализация знаний. (8 мин.)
Из домашней работы на доске рассмотреть № 214(а).
Записать:
-
20 относится к 10, так же как 300 относится к 150.
-
72 так относится к 8, как 24 относится к 3.
-
Отношение 4 к 8 равно отношению 0,25 к 0,5.
-
7 составляет такую же часть от 70, какую 6 составляет от 60.
-
66 во столько раз больше 11, во сколько раз 42 больше 7.
На доске записать числа, из которых ученики должны составить пропорции: 8, 2, 6, 4, 24.
3. Новый материал. (10 мин.)
После выполнения последнего задания преподаватель и ученики должны вывести правило нахождения неизвестного члена пропорции. Правила проговариваются несколько раз и на доске рассматриваются уравнения № 200 (а, г, ж, к). Уравнения из данного номера решаются с полным объяснением. При малейшем затруднении преподаватель объясняет уравнение сам.
4. Закрепление нового материала. (20 мин.)
Задание № 200 (б, д, з, л) решается учениками самостоятельно, а затем, устно проверяется.
Так же разобрать номера № 202, 204, 207, 208, 216.
Рассмотреть решение сложных уравнений:
а) 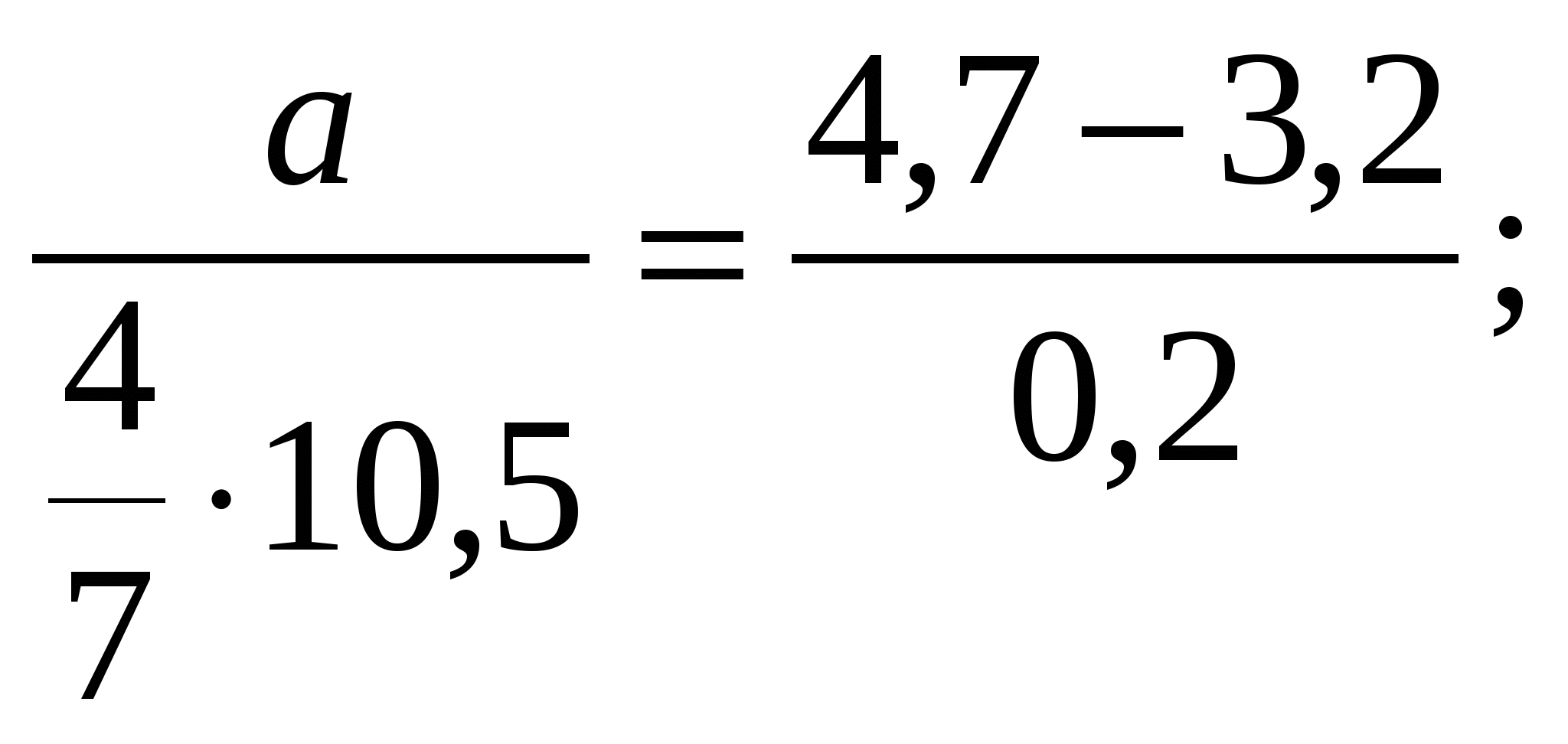 б)
б) 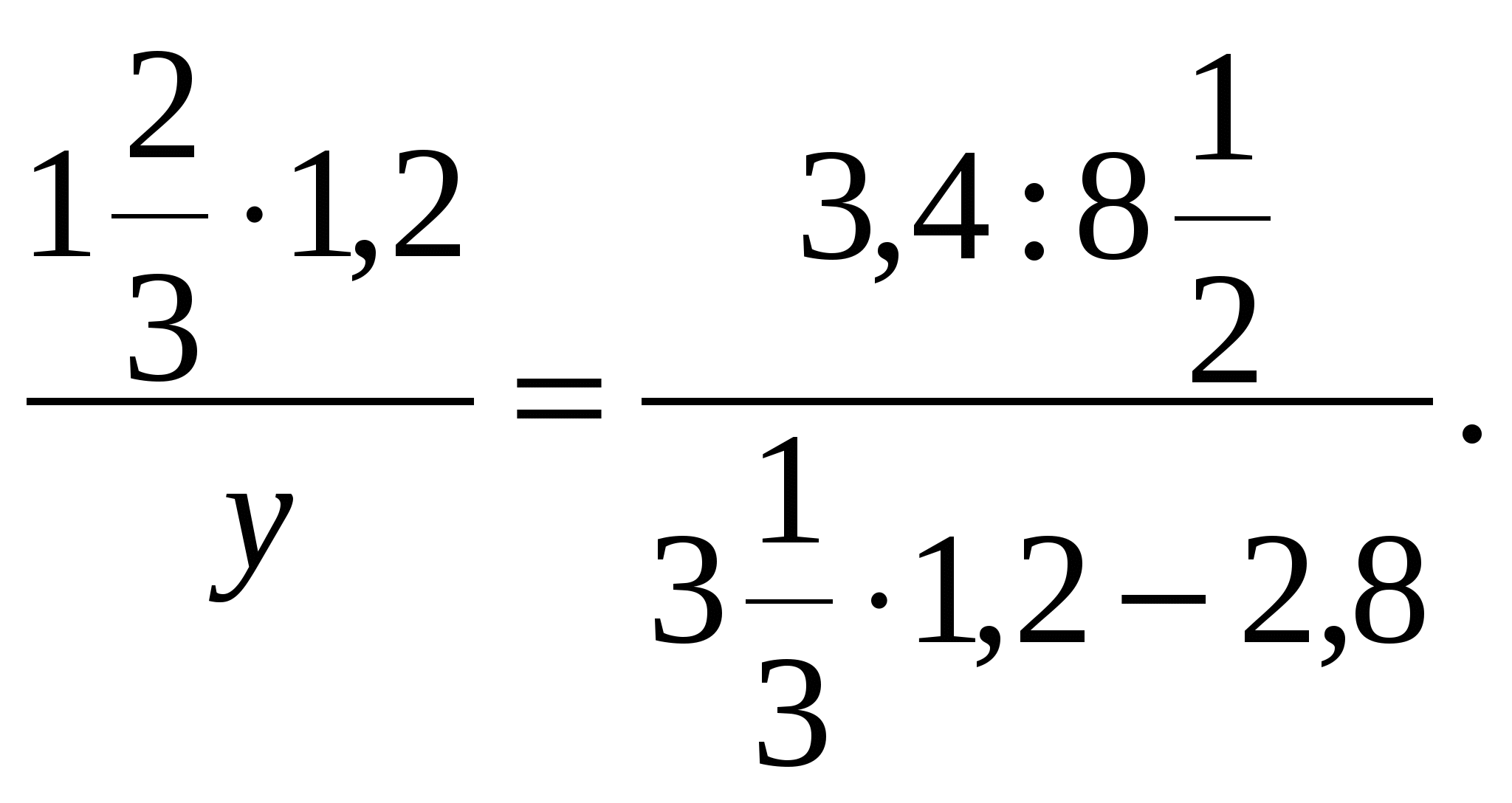
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 2.3.
Решить задания № 200 (в, е, и, м), 205, 206.
Урок 19. Пропорции
Тема: Пропорции.
Цели урока: повторить и закрепить понятие пропорции, ее крайних и средних членов, основное свойство пропорции; объяснить правила нахождения неизвестных членов пропорции; показать правила решения уравнений и задач на пропорции. В течение урока развивать у учащихся навык решения уравнений и задач на пропорцию.
Ход урока:
1. Организационный момент. (2 мин.)
2. Актуализация знаний. (8 мин.)
Из домашней работы на доске рассмотреть № 214(а).
Записать:
-
20 относится к 10, так же как 300 относится к 150.
-
72 так относится к 8, как 24 относится к 3.
-
Отношение 4 к 8 равно отношению 0,25 к 0,5.
-
7 составляет такую же часть от 70, какую 6 составляет от 60.
-
66 во столько раз больше 11, во сколько раз 42 больше 7.
На доске записать числа, из которых ученики должны составить пропорции: 8, 2, 6, 4, 24.
3. Новый материал. (10 мин.)
После выполнения последнего задания преподаватель и ученики должны вывести правило нахождения неизвестного члена пропорции. Правила проговариваются несколько раз и на доске рассматриваются уравнения № 200 (а, г, ж, к). Уравнения из данного номера решаются с полным объяснением. При малейшем затруднении преподаватель объясняет уравнение сам.
4. Закрепление нового материала. (20 мин.)
Задание № 200 (б, д, з, л) решается учениками самостоятельно, а затем, устно проверяется.
Так же разобрать номера № 202, 204, 207, 208, 216.
Рассмотреть решение сложных уравнений:
а) 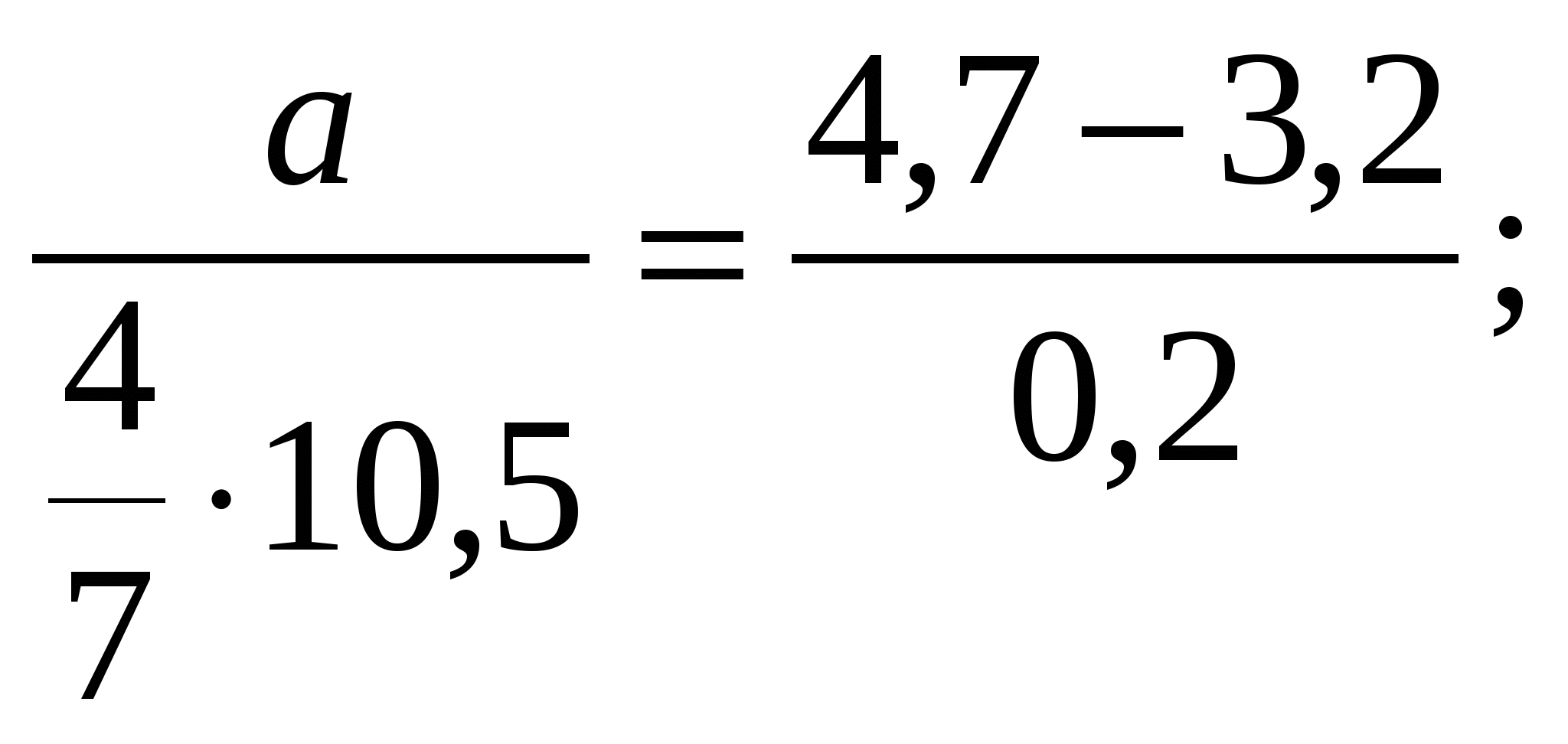 б)
б) 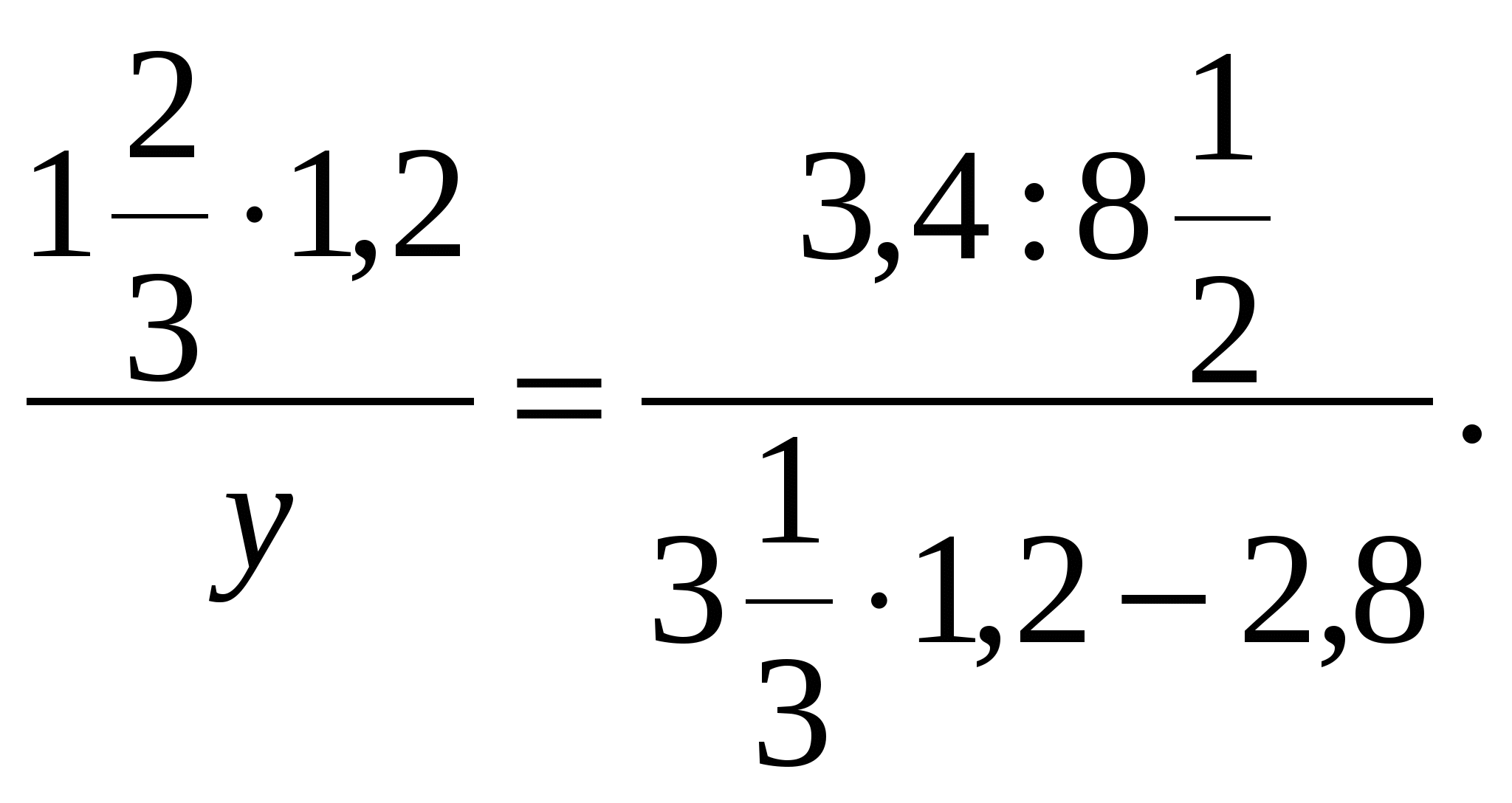
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 2.3.
Решить задания № 200 (в, е, и, м), 205, 206.
Урок 20. Прямая и обратная пропорциональности
Тема: Прямая и обратная пропорциональности.
Цели урока: объяснить понятие прямой и обратной пропорций; показать правила проверки на прямую и обратную пропорции; проверить знания учащихся по пропорции. В течение урока развивать у учащихся навык проверки пропорциональностей.
Ход урока:
1. Организационный момент. (2 мин.)
2. Математический диктант. (10 мин.)
| Вариант 2 | |
| 1) В группе детского сада 4 мальчика и 8 девочек. | |
| Какую часть мальчики составляют от количества девочек? | Какую часть количество мальчиков составляет от числа всех детей. |
| 2) Разложить число 240 на два числа в данном отношении. | |
| 2 : 3 | 1 : 5 |
| 3) Найти неизвестный член пропорции | |
| 5 : x = 3 : 2,4 | 4 : 0,6 = 8 : y |
| 4) Построить отрезок AB равный 12 сантиметрам и отметить на этом отрезке точку С, делящую отрезок в данном отношении | |
| 1 : 3 | 1 : 2 |
Математический диктант проверяется сразу на уроке и ошибки (если встречаются у многих учеников) разбираются на доске.
3. Новый материал. (8 мин.)
Для объяснения сначала ответить на вопросы по данному условию. «Мы взяли деньги, и пошли покупать конфеты»
-
На что влияет количество конфет, которое мы купим?
-
Чем больше конфет мы покупаем, тем …
-
На что влияет стоимость конфет?
-
Чем дороже конфеты, тем …
В данном случае сначала разбираются ситуации, в которых с увеличением одной величины увеличивается другая. И потом ситуации в которых с увеличением другой величины уменьшается другая. Затем дать возможность детям придумать аналогичные ситуации. И только после этого, преподаватель объясняет, что если изменение в одинаковое количество раз, то это пропорции (прямая и обратная пропорции). Дать определение данным пропорциям.
4. Закрепление нового материала. (20 мин.)
Разобрать задачи № 217, 219.
Затем устно рассматриваются задания № 220, 223, и письменно задачи № 221, 225, 232, 235, 249. (Задачи можно оформлять в виде таблиц)
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 2.4.
Решить № 222, 224, 228.
Урок 21. Прямая и обратная пропорциональности
Тема: Прямая и обратная пропорциональности.
Цели урока: повторить и закрепить понятия прямой и обратной пропорций, правила проверки на прямую пропорциональность и обратную пропорциональность; проверить знания учащихся по прямой и обратной пропорциональностей. В течение урока развивать у учащихся навык проверки пропорциональностей.
Ход урока:
1. Организационный момент. (2 мин.)
2. Устная работа. (10 мин.)
Устно разбираются задания № 231, 241, 242, 243. Кроме решения в каждом из этих заданий ученики должны говорить, о какой пропорциональности идет речь, и знать определении данной пропорциональности.
3. Решение задач. (10 мин.)
Решить задачу. «За 3 килограмма конфет заплатили 216 рублей. Сколько денег заплатят, если купят 2 кг, 5 кг, 10 кг?»
Затем к доске вызывается один ученик из первого варианта, один из второго. Они выполняют задания № 246 и 246. Все остальные ученики выполняют оба этих номера, а затем сверяются с доской. Затем на доске разбираются задачи № 251, 253.
4. Самостоятельная работа. (18 мин.)
| Вариант 2 | |
| № 226, 229, 233, 236 | № 227, 230, 234, 237 |
Какие-то из данных задач, по усмотрению преподавателя, можно одновременно решить на закрывающихся досках и проверить прямо на уроке.
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 2.4.
Решить задания № 240, 245, 250.
Тема: Решение задач на прямую и обратную пропорциональности с помощью пропорций.
Цели урока: повторить и закрепить понятия прямой и обратной пропорций; объяснить правила решения задач на прямую и обратную пропорциональности; проверить знания учащихся по пропорции. В течение урока развивать у учащихся навык решения задач на пропорциональности.
Ход урока:
1. Организационный момент. (2 мин.)
2. Анализ самостоятельной работы. (3 мин.)
3. Устная работа. (5 мин.)
Вспомнить определения прямой и обратной пропорциональностей. Определить каждое из данных условий, какой пропорциональностью оно является.
В ремонте школы помогали старшеклассники. В первый день пришли 4 старшеклассника и покрасили 20 парт, во второй день пришло 7 старшеклассников и покрасило 35 парт.
На 2 платья надо 3м. ткани, а на 5 платьев – 7,5м.
В день нужно сдать 10 мешков картошки 5 колхозников на сбор картошки потратили 4 часа. А в другом колхозе работало 10 колхозников и им потребовалось всего 2 часа.
Для проведения экзамена в 11 «А» класс купили 24 ручки и заплатили 72 рубля. А в 11 «В» 27 человек и купив для этого класса ручки, заплатили 81 рубль.
На зиму запасают на одну семью 24 кг лука. Семье в которой 3 человека лука хватает на 4 месяца. А если в семье 6 человек, то лука хватает на два месяца.
4. Новый материал. (10 мин.)
Для объяснения нового материала в первом и пятом условиях из устного счета вводятся неизвестные величины. И объясняется правило решения данного вида задач. После чего записывается алгоритм решения задач.
-
Определить вид пропорциональности.
-
Составить пропорцию
-
Решить уравнение на пропорцию.
Для слабых учеников показать, что после определения вида пропорции можно поставить стрелки, которые помогут правильно составить пропорцию.
5. Закрепление нового материала. (10 мин.)
Рассмотреть задачи № 255, 258 (по рядам), 265, 267.
6. Закрепление – тестирование. (10 мин.)
Вариант 1.
1. В банке засолили 14 огурцов и 4 помидора. Какую часть составляют помидоры от всех засоленных овощей?
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
2. Число 30 разделили на сумму трех положительных чисел в отношении 2:3:5. Найдите наименьшее из получившихся чисел.
1) 1; 2) 3; 3) 5; 4) 6.
3. Выберете из данных пропорций верную
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
4. Найдите неизвестный член пропорции ![]()
1) 3; 2) 30; 3) 0,3; 4) 300.
5. Дед Мороз на Новый Год приготовил 6 коробок для игрушек, каждой из которых помещается по 380 штук. Но при перевозке коробки повредились и игрушки переложили в другие коробки, в которые помещается 456 штук. Сколько понадобится таких коробок, чтобы поместились все игрушки?
1) 5; 2) 7; 3) 4; 4) 9.
Вариант 2.
1. На зиму бабушка закрутила 6 банок малинового варения и 9 банок абрикосового джема. Какую часть составляет лечебное малиновое варенье от всей бабушкиной закрутки?
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
2. Число 40 разделили на сумму трех положительных чисел в отношении 2:2:4. Найдите наибольшее из получившихся чисел.
1) 16; 2) 20; 3) 10; 4) 24.
3. Выберете из данных пропорций не верную
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
4. Найдите неизвестный член пропорции ![]()
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
5. В оздоровительный лагерь готовились отправить 360 кг картошки на 135 человек одной смены. Но стало известно, что в лагере будет 120 человек. Сколько килограмм картошки нужно отправить в лагерь, если расход картошки на одного человека не изменится?
1) 320; 2) 350; 3) 405; 4) 300.
ОТВЕТЫ
| 1 | 2 | 3 | 4 | 5 | |
| Вариант 1 | 3 | 4 | 4 | 2 | 1 |
| Вариант 2 | 3 | 2 | 4 | 3 | 1 |
7. Итоги урока. (3 мин.)
8. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 2.5.
Решить задания № 257, 259, 261, 266.
Урок22Решение задач на прямую и обратную пропорциональности с помощью пропорций
Тема: Решение задач на прямую и обратную пропорциональности с помощью пропорций.
Цели урока: повторить и закрепить правила решения задач на прямую и обратную пропорциональности; проверить умение учащихся решать задачи на данную тему, рассмотреть задачи – шутки на данную тему для повышения интереса к математике. В течение урока развивать у учащихся навык решения задач на пропорциональности.
Ход урока:
1. Организационный момент. (2 мин.)
2. Устная работа. (6 мин.)
|
|
|
Сначала решаются примеры по цепочке, а затем уравнения, которые лучше сделать на карточках.
3. Индивидуальный опрос. (7 мин.)
К доске вызывается 4 ученика, которые решают задачи по карточкам.
| Карточка 2. Теплоход проходит свой маршрут со скоростью 50 км/ч за 4,8 часа. С какой скоростью должен идти теплоход, чтобы пройти это расстояние за 3,2 часа? |
| Карточка 3. За 0,9 кг мяса заплати 72 рубля. Сколько можно купить мяса на 160 рублей? |
| Карточка 4. Для завоза песка на стройку надо 10 грузовиков грузоподъемностью 6 тонн. Сколько потребуется грузовиков, если грузоподъемность будет 12 тонн? |
Остальные ученики в это время решают № 260. На решение дается 5 минут, после этого проверяются задачи, решенные на доске. Ученики, которые решали эти задачи, должны объяснить свое решение. Затем проверяется задача № 260 (устно).
4. Решение задач. (10 мин.)
Разбираются задачи № 268, 270, 273.
Так же решаются следующие задачи:
1) На Новый год в шестой класс принесли два торта. Один торт съели мальчики, а другой - девочки. В классе 15 мальчиков и они справились с тортом за 8 минут. Сколько минут понадобится девочкам, чтобы от торта не осталось ни крошки, если торт едят они с той же скорость, что и мальчики и в классе их 12?
2) Паша и Слава решили списать домашнее задание у Светы. Паше бежать до Светы пришлось 120 метров, и через 3 минуты он уже приступил к списыванию. А Слава живет от Светы на расстоянии 160 метров, и бегает с той же скоростью, что и Паша. Через сколько минут Слава приступит к "выполнению" домашнего задания?
5. Самостоятельная работа. (15 мин.)
| Вариант 2. | |
| 1) Построить прямоугольник, периметр которого равен 24 см, а стороны соотносятся в данном отношении. | |
| 1 : 2 | 1 : 5 |
| 2) Решить уравнение на пропорцию. | |
| 1,3 : 3,9 = |
|
| 3) № 269 | 3) № 271 |
6. Итоги урока. (3 мин.)
7. Домашнее задание. (2 мин.)
Ответить на вопросы для повторения главы 2 (стр. 70 – 71). Письменно ответить на вопросы 6, 7, 8, 10.
Решить задания № 272, 274.
Урок 24. Подготовка к контрольной работе
Тема: Подготовка к контрольной работе.
Цели урока: повторить и закрепить определения отношения, пропорции, прямой и обратной пропорциональностей, правила решения задач на прямую и обратную пропорциональности; рассмотреть задачи – шутки на данную тему для повышения интереса к математике. В течение урока развивать у учащихся навык решения уравнений и задач на пропорциональности.
Ход урока:
1. Организационный момент. (2 мин.)
2. Анализ самостоятельной работы. (3 мин.)
Разобрать задачи, с которыми не справили ученики (если такие задачи есть).
3. Решение уравнений. (10 мин.)
На доске должны быть записаны уравнения на пропорцию.
1) ![]() 2)
2) ![]() 3)
3) ![]()
4) ![]() 5)
5) ![]() 6)
6) ![]()
7) ![]() 8)
8) ![]()
9) ![]()
Каждый ученик должен выбрать три уравнения и решить их самостоятельно в тетрадях. Затем на магнитной доске появляются карточки с числами, на обратной стороне которых буквы.
| Р – 1 | О – 3 | Ц – | И – 2 | Я – 1,8 |
Так же на доске появляются 9 ячеек для букв слова. И в них записываются буквы, которые соответствуют ответам уравнений. Должно получиться слово «ПРОПОРЦИЯ». Если какое-то уравнение не решил никто из учеников, то оно решается на доске. После того, как появилось слово на доске, надо обсудить с учениками, были ли уравнения, которые вызвали затруднения.
4. Решение задач. (25 мин.)
Решить задачи.
1) Катя, Оля и Наташа собрали ракушки на берегу в отношении ![]() . Сколько ракушек собрала каждая девочка, если всего они собрали 120 штук.
. Сколько ракушек собрала каждая девочка, если всего они собрали 120 штук.
2) Из заданий для самопроверки решить задания № 1, 3, 5, 9, 11.
3) Преподаватель объясняет решение задачи № 275, а затем вместе с учениками разбирается задача № 277.
4) Лена получила зарплату и пошла в магазин. В магазине она долго выбирала, что купить, и приобрела 3 блузки за 2451 рубль. Но, подумав, решила, что если не купит еще 2 блузки, то ходить на работу ей будет не в чем. Сколько еще заплатит Лена, если в магазине все блузки по одной цене?
5) В квартире затеяли ремонт, и Маша с братом Алешей решили оставить свои автографы на старых обоях. Маша за 33 минуты нарисовала 6 девочек, а ее брат, рисуя с той же скоростью, нарисовал 10 машинок. Сколько времени потребовалось Алеше, чтобы его узнали потомки?
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Из заданий для самопроверки решить задания № 2, 4, 7, 8, 12.
Сильным ученикам дополнительно задается задача № 278.
Урок 25. Контрольная работа
Тема: Контрольная работа.
Цели урока: проверить знания учеников по данной теме.
Ход урока:
1. Организационный момент.
2. Контрольная работа.
Вариант 1.
1. Петр Иванович в магазине потратил 900 рублей, из них на сладости ушло 135 рублей. Какую часть от стоимости покупок составляет стоимость сладкого? Сколько процентов стоимость сладкого составляет от всех потраченных денег?
2. Отрезок длиной 7,2 см. разделен двумя точками на три отрезка в отношении 1:2:3. Найдите длину самого длинного из получившихся отрезков.
3. Используя свойство пропорции найти неизвестный член пропорции: а) ![]() б)
б) ![]() .
.
4. За 2,5 часа черепаха проползла 300 метров. За какое время она проползет еще 240 метров, если ее скорость не изменится?
5. Два участка дороги одинаковой длины взялись ремонтировать две бригады. Производительность первой бригады 120 метров в час, а второй – 180 метров в час. Первая бригада отремонтировала свой участок за 6 часов. За сколько часов отремонтировала свой участок вторая бригада?
Вариант 2
1. Из 28 учеников в классе 10 человек дополнительно занимаются английским языком. Какую часть класса они составляют? Сколько процентов от класса они составляют?
2. Отрезок длиной 6,4 см. разделен двумя точками на три отрезка в отношении 5:6:5. Найдите длину самого короткого из получившихся отрезков.
3. Используя свойство пропорции найти неизвестный член пропорции: а) ![]() б)
б) ![]() .
.
4. За 3,5 часа рабочие украсили 420 метров центральной набережной. Сколько метров улицы успеют украсить рабочие за оставшиеся три часа, если производительность не изменится?
5. Два участка дороги одинаковой длины взялись ремонтировать две бригады. Производительность первой бригады 160 метров в час, а второй – 120 метров в час. Первая бригада отремонтировала свой участок за 6 часов. За сколько часов отремонтировала свой участок вторая бригада?
3. Домашнее задание.
Решить задания № 6, 10 (стр. 72), № 276.
Урок 26. Буквенные выражения и числовые подстановки
Тема: Буквенные выражения и числовые подстановки.
Цели урока: объяснить понятия буквенного и числового выражений, переменной; проанализировать контрольную работу и закрепить пройденную тему; рассказать об истории алгебры. В течение урока развивать у учащихся навык работы с буквенными выражениями.
Ход урока:
1. Организационный момент. (2 мин.)
2. Анализ контрольной работы. (8 мин.)
Разобрать задания из контрольной работы, при решении которых было допущено наибольшее количество ошибок. Для закрепления пройденной темы также предлагается решить следующие задания:
1) Число 612 представить в виде суммы трех слагаемых, которые относятся, как 2: 3: 4. Найти сумму большего и меньшего слагаемых.
2) Найти неизвестный член пропорции:
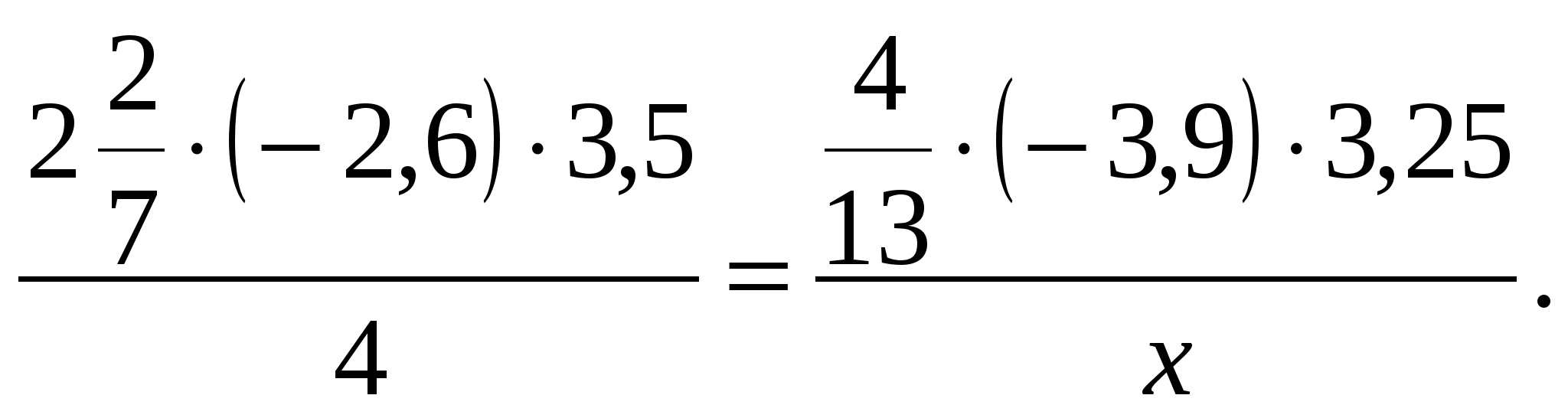
3. Новая тема. (15 мин.)
Можно начать с небольшой лекции о развитии алгебры в различных частях света.
Вавилон. Истоки алгебры восходят к глубокой древности. Уже около 4000 лет назад вавилонские ученые владели решением квадратного уравнения и решали системы двух уравнений, из которых одно - второй степени. С помощью таких уравнений решались разнообразные задачи землемерия, строительного искусства и военного дела.
Буквенные обозначения, применяемые нами в алгебре, не употреблялись вавилонянами; уравнения записывались в словесной форме.
Китай. За 2000 лет до нашего времени китайские ученые решали уравнения первой степени и их системы, а также квадратные уравнения. Им были знакомы отрицательные и иррациональные числа. Так как в китайском письме каждый знак изображает некоторое понятие, то в китайской алгебре не могло быть "сокращенных" обозначений.
В последующие эпохи китайская математика обогатилась новыми достижениями. Так в конце 13 века китайцы знали закон образования биноминальных коэффициентов, известный ныне под именем "треугольник Паскаля". В Западной Европе этот закон был открыт (Штифелем) на 250 лет позднее.
Страны арабского языка. Узбекистан. Таджикистан. У индийских авторов алгебраические вопросы излагались в астрономических сочинениях; самостоятельной дисциплиной алгебра становится у ученых, писавших на международном языке мусульманского мира - арабском. Основоположником алгебры, как особой науки нужно считать среднеазиатского ученого Мухаммеда из Хорезма, известного под арабским прозвищем Аль-Хоризми (Хорезмиенец). Его алгебраический труд, составленный в 9 в. н. э., носит название "Книга восстановления и противопоставления". "Восстановлением" Мухаммед называет перенос вычитаемого из одной части уравнения в другую, где оно становится слагаемым; "противопоставлением" - собирание неизвестных в одну сторону уравнения, а известных - в другую сторону. На арабском языке "восстановление" называется "ал-джебр". Отсюда и название "алгебра".
У Муххамеда Хорезмского и у последующих авторов алгебра широко применяется к купеческим и иным денежным расчетам. Ни он, ни другие математики, писавшие на арабском языке, не употребляли никаких сокращенных обозначений. (В них не было нужды, ибо арабское письмо очень кратко: гласные не обозначаются, согласные и полугласные буквы просты по начертанию и сливаются по нескольку в один знак.) Они не признавали и отрицательных чисел: учение об отрицательных числах, знакомое им из индийских источников, они считали плохо обоснованными. Это было справедливо, но зато индийские ученые могли ограничиться одним случаем полного квадратного уравнения, тогда как Мухаммед Хорезмский и его преемники должны были различать три случая (x2+px=q, x2+q=px, x2=px+q; p и q - положительные числа).
Средневековая Европа. В 12 веке "Алгебра" Аль-Хорезми стала известна в Европе и была переведена на латинский язык. С этого самого времени начинается развитие алгебры в европейских странах (сначала под сильным влиянием науки восточных народов). Появляются сокращенные обозначения неизвестных, решается ряд новых задач, связанных с потребностями торговли. Но существенного сдвига не было до 16 века. В первой трети 16 века итальянцы Дель-Ферро и Тарталья нашли правила для решения кубических уравнений вида x3=px+q; x3+px=q; x3+q=px. А Кардане в 1545 г. показал, что всякое кубическое уравнение сводится к одному из этих трех; в это же время Феррари, ученик Кардана, нашел решение уравнения четвертой степени.
Для объяснения новой темы на доске должны быть записаны выражения:
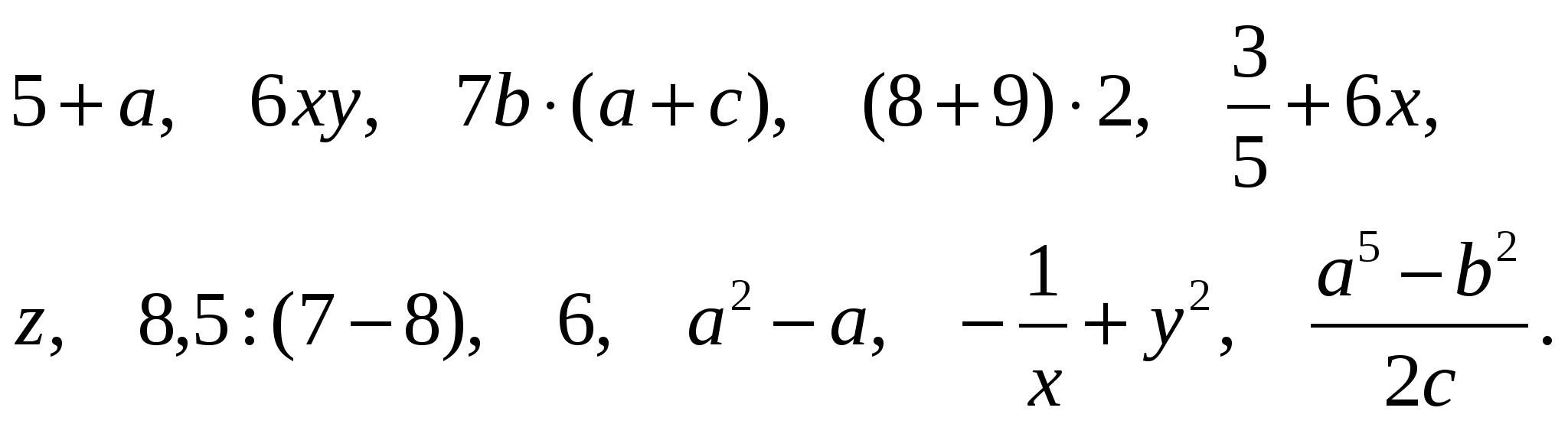
Ученики самостоятельно должны постараться выбрать из данных выражений буквенные. Те выражения, которые, по их мнению, не являются буквенными – зачеркиваются. Затем преподаватель дает определение буквенным выражениям и проверяет, на сколько верно ученики выполнили задание. Так же вводится понятие переменной и рассказывается о сокращении записи в буквенных выражениях. После этого ученики по данным выражениям должны ответить на следующие вопросы.
-
Является ли данное выражение буквенным?
-
Сколько действий в данном выражении?
-
Сколько переменных содержится в данном выражении?
-
Какие переменные участвуют в записи?
-
Вычислить значение выражения, если вместо всех переменных подставить 2. (Для всех ли выражений достаточно замены одной переменной?)
4. Закрепление нового материала. (15 мин.)
Решить задания № 281, 283, 282 (а и б вычисляются всем классом, в и г даются по вариантам и сравниваются варианты).
Также выполняются задания № 288 (объясняя значение скобок), 300.
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 3.1.
Решить задания № 284, 285, 301, 304.
Урок 27. Буквенные выражения и числовые подстановки
Тема: Буквенные выражения и числовые подстановки.
Цели урока: закрепить и повторить понятия буквенного и числового выражений, переменной; объяснить правила решения и оформления задач с переменными; рассмотреть решение задач – шуток, для развития у детей заинтересованности математикой. В течение урока развивать у учащихся навык решения задач с переменными.
Ход урока:
1. Организационный момент. (2 мин.)
2. Устная работа. (5 мин.)
На карточках или на доске записаны выражения.
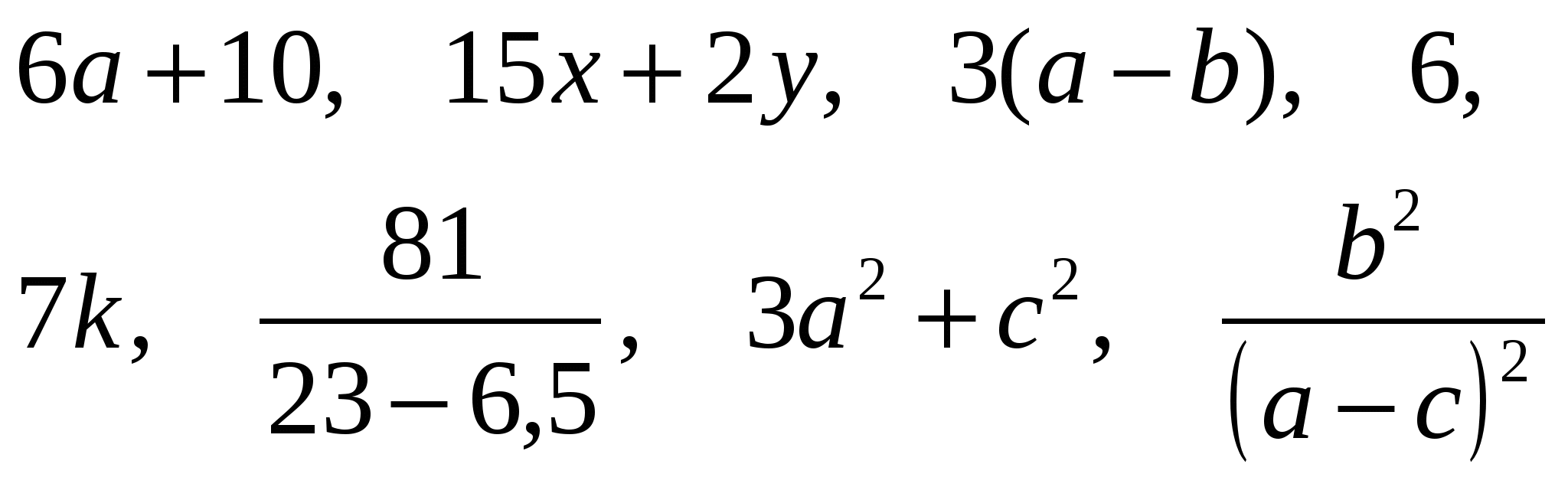
Для каждого из выражений ученики должны ответить на следующие вопросы.
-
Является ли буквенным данное выражение?
-
Сколько действий содержит данное выражение?
-
Сколько переменных содержится в данном выражении?
Также на доске рассмотреть задание № 301 из домашнего задания.
3. Актуализация знаний. (14 мин.)
Для закрепления понятия буквенных выражений и вычисления их значений разобрать задания № 307 (а, в), 308, 302. Перед тем, как выполнить последний номер вспомнить определение и привести примеры противоположных чисел и взаимообратных.
4. Новый материал. (9 мин.)
Ввести понятие равенства буквенных выражений. Разобрать задачу № 290. Рассказать о значениях алгебраических выражениях при решении задач. Показать правила решения и оформления таких задач на № 291.
5. Закрепление нового материала. (10 мин.)
Решить задачи № 293, 295, 298, 299 (а), 305.
Также рассмотреть решение задач - шуток:
1) У Коли было a марок, а у Сережи на 8 марок больше. Во время игры Сережа сначала проиграл b марок, а затем выиграл 7. Сколько марок стало у каждого мальчика после игры? У кого из мальчиков стало больше марок и на сколько, если a = 14, b = 13.
2) Катя и Нина на берегу моря собирали ракушки. Но девочки поссорили и разделили ракушки, у Кати осталось x ракушек, а у Нины - y. Пока девочки были в ссоре, Катя нашла еще 7 ракушек, Нина нашла 11 ракушек. Потом девочки помирились и дали клятву, никогда не ссорится, и только после этого объединили богатства - ракушки. Сколько всего стало у девочек ракушек? Найдите значение, если x = 17, y = 15.
6. Итоги урока. (3 мин.)
7. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 3.1.
Решить задания № 299 (б), 292, 307 (б, г), 303.
Урок 28. Буквенные выражения и числовые подстановки
Тема: Буквенные выражения и числовые подстановки.
Цели урока: закрепить и повторить понятия буквенного и числового выражений, переменной. В течение урока развивать у учащихся навык нахождения значений буквенных выражений и решения задач с переменными.
Ход урока:
1. Организационный момент. (2 мин.)
2. Индивидуальный опрос. (8 мин.)
К доске приглашается 4 ученика для работы по карточкам.
| Карточка 2. Для каждого из выражений подберите |
| Карточка 3. Карандаш стоит a рублей, стоимость ручки b рублей. Сколько заплатили за 5 карандашей и 3 ручки? |
| Карточка 4. Карандаш стоит a рублей, стоимость ручки b рублей. Объясните смысл данных выражений:
|
Остальные ученики в этот момент устно вычисляют:
![]() при
при ![]()
![]() при
при ![]()
Затем каждая из карточек разбирается и проверяется всем классом.
3. Решение задач. (15 мин.)
Разобрать задания № 311, 312, 313, 315, 317, 319.
Также рассмотреть задания повышенной трудности:
1) Найти ![]() , если
, если ![]() и
и ![]() .
.
2) Вычислить значение выражения ![]() , если
, если ![]()
![]()
![]()
4. Самостоятельная работа. (15 мин.)
| Вариант 2 | |
| № 286 (а, в), 296, 298 (в) | № 286 (б, г), 297, 298 (г) |
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 3.1.
Решить задания № 294, 314, 316, 318.
Урок 29. Буквенная запись свойств действий над числами
Тема: Буквенная запись свойств действий над числами.
Цели урока: вспомнить и повторить свойства действий над числами. В течение урока развивать у учащихся навык записывать свойства при помощи буквенных равенств.
знать; уметь Ход урока:
1. Организационный момент. (2 мин.)
2. Анализ самостоятельной работы. (8 мин.)
Разобрать задания, в которых при выполнении самостоятельной работы было допущено наибольшее количество ошибок.
Для актуализации знаний из домашней работы проверяется № 318, и выполняются № 320, 306.
Разобрать задание повышенной трудности:
Вычислить значение выражения ![]() , если
, если ![]()
![]()
![]()
3. Новый материал. (12 мин.)
Преподаватель вместе с учениками вспоминает свойство действий: переместительное, сочетательное и распределительное. Записываются эти свойства на доске, а лучше на плакате. Затем преподаватель объясняет ученикам, что запись данных правил с помощью букв является буквенной записью свойств действий – формулами.
4. Закрепление нового материала. (18 мин.)
Разобрать задания № 321, 322, 323, 325, 327, 328 и 331.
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 3.2.
Решить задания № 309, 324, 326, 329,
Урок 30. Преобразование буквенных выражений
Тема: Преобразование буквенных выражений.
Цели урока: проверить умение учащихся записывать свойства действий над числами с помощью буквенных выражений; объяснить правила преобразования буквенных выражений и определение числового коэффициента. В течение урока развивать у учащихся навык упрощать выражения и находить числовой коэффициент произведения.
Ход урока:
1. Организационный момент. (2 мин.)
2. Актуализация знаний. (5 мин.)
Провести математический диктант для всего класса. Один из учеников записывает его на закрывающейся доске.
Запишите с помощью букв данные выражения:
-
Переместительный закон сложения
-
Правило деления суммы трех чисел на некоторое число
-
Правило сложения обыкновенных дробей
-
Правило деления обыкновенных дробей
-
Распределительный закон
Затем проверяется правильность записи на доске, а ученики, обменявшись тетрадями, по парам проверяют математический диктант друг у друга. После чего нужно вспомнить определение буквенного выражения.
3. Новый материал. (8 мин.)
Дать правило объединяющее переместительный и сочетательный законы относительно сложения (умножения). Затем рассматривается пример по данным правилам.
-
Записать сумму выражений
 в нескольких вариантах:
в нескольких вариантах: 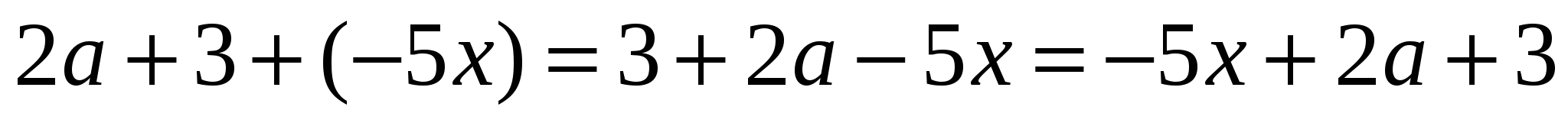
-
Записать произведение этих же выражений в нескольких вариантах:
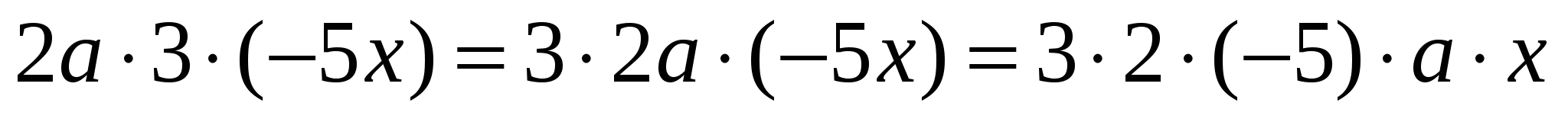
Объяснить, что в последнем примере выражения можно раскладывать на компоненты, а следовательно перейти к упрощению данного выражения.
![]()
Ввести понятие числового коэффициента.
4. Закрепление нового материала. (25 мин.)
Разобрать задания № 336, 337, 338, 340, 343 (а), 345 и 349.
Так же можно, если достаточно времени, разобрать следующее задание.
В данное выражение вместо переменной ![]() подставить выражение
подставить выражение ![]() и указать натуральные числа, на которые получившееся выражение будет делиться без остатка:
и указать натуральные числа, на которые получившееся выражение будет делиться без остатка:
а) ![]() б)
б) ![]() в)
в) ![]()
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 3.3.
Решить задания № 339, 341, 347 и 343 (б).
Урок 31. Преобразование буквенных выражений
Тема: Преобразование буквенных выражений.
Цели урока: повторить и закрепить правила преобразования буквенных выражений, определение числового коэффициента; разобрать правила сокращения дробей; проверить знания и умения учащихся, по упрощению выражению и нахождению числового коэффициента любого произведения. В течение урока развивать у учащихся навык упрощать выражения и находить числовой коэффициент произведения.
Ход урока:
1. Организационный момент. (2 мин.)
2. Устная работа. (5 мин.)
Задания заранее записываются на доске или оформляются в виде карточек.
-
Назовите слагаемые данного буквенного выражения и числовой коэффициент каждого слагаемого
![]()
-
Вычислить числовой коэффициент произведения и назвать его буквенную часть
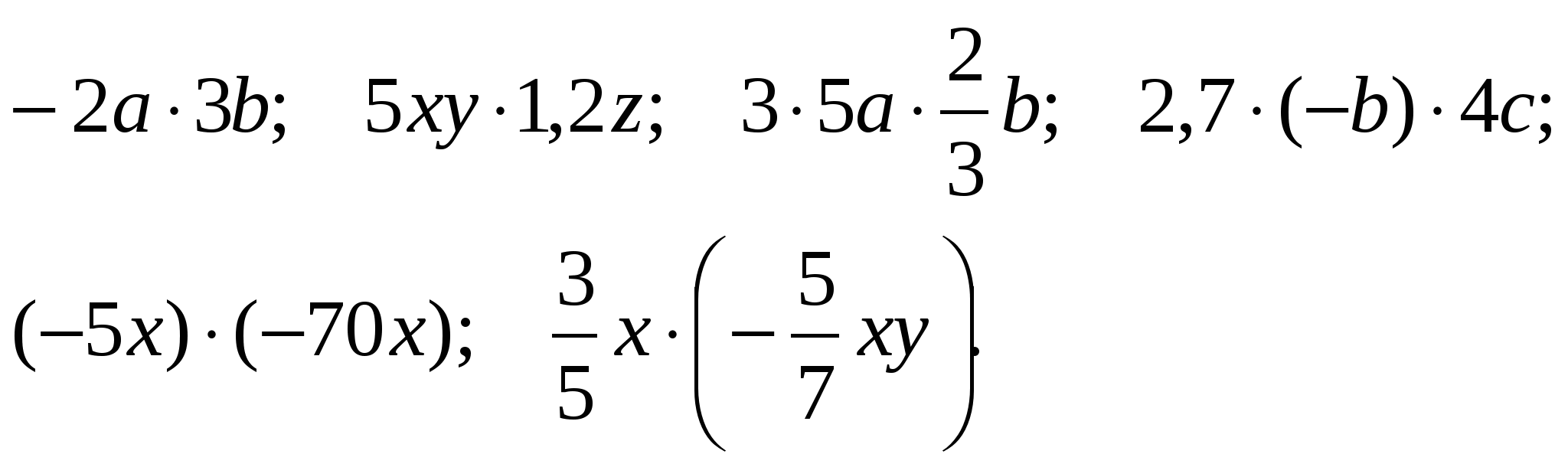
3. Решение задач. (23 мин.)
Решить задания № 342, 346, 348, 351 и 354.
Так же разобрать более сложное задание.
Сократить дроби и найти значения получившихся выражений при заданных переменных:
а) ![]() б)
б) ![]()
в) ![]()
4. Самостоятельная работа. (10 мин.)
| Вариант 2 | |
| 1. Упростить выражение. | |
|
|
|
| 2. Упростить произведение и подчеркнуть числовой коэффициент | |
|
|
|
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 3.3.
Решить задания № 344, 350, 352.
Урок 32. Преобразование буквенных выражений
Тема: Преобразование буквенных выражений.
Цели урока: повторить и закрепить правила преобразования буквенных выражений, определение числового коэффициента. В течение урока развивать у учащихся навык упрощать выражения, находить числовой коэффициент произведения, сокращать дроби и упрощать выражения со степенями.
Ход урока:
1. Организационный момент. (2 мин.)
2. Анализ самостоятельной работы. (3 мин.)
Выставить оценки в журнал и разобрать те примеры, в которых было допущено наибольшее количество ошибок.
3. Актуализация знаний. (10 мин.)
У доски разобрать следующие задания
-
Упростить выражение:
-
-
Упростить выражение и подчеркнуть числовой коэффициент (обратить внимание каким образом произведение упрочатся в степень):
-
4. Решение задач. (25 мин.)
Рассмотреть задания № 355, 358, 359, 361, 362 (б) и 364.
Так же рассмотреть задачу.
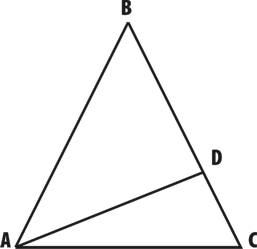
Составить выражение показывающие периметр треугольника ABC, если DC = a, AD = b, BD в два раза больше DC, AB = BC, AC на 1 см больше, чем AD. Вычислить периметр данного треугольника, если a = 3 см,b = 4 см.
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 3.3.
Решить задания № 356, 360, 363 и 362 (а).
Урок 63. Произведение и частное степеней
Тема: Произведение и частное степеней.
Цели урока: провести анализ контрольной работы, закрепить пройденный материал; вспомнить понятие степени; объяснить правила произведения и частного степеней. В течение урока развивать у учеников навык вычислять степень заданного числа, упрощать произведение и частное степеней.
Ход урока:
1. Организационный момент. (2 мин.)
2. Анализ контрольной работы. (8 мин.)
Выставить оценки за контрольную работу. Разобрать на доске задания из контрольной работы, по которым было допущено наибольшее количество ошибок. Для закрепления пройденного материала разобрать следующие задания:
1) На координатной плоскости постройте график зависимости: ![]() . Изобразите прямую, симметричную ей относительно оси абсцисс.
. Изобразите прямую, симметричную ей относительно оси абсцисс.
2) Постройте график зависимости: 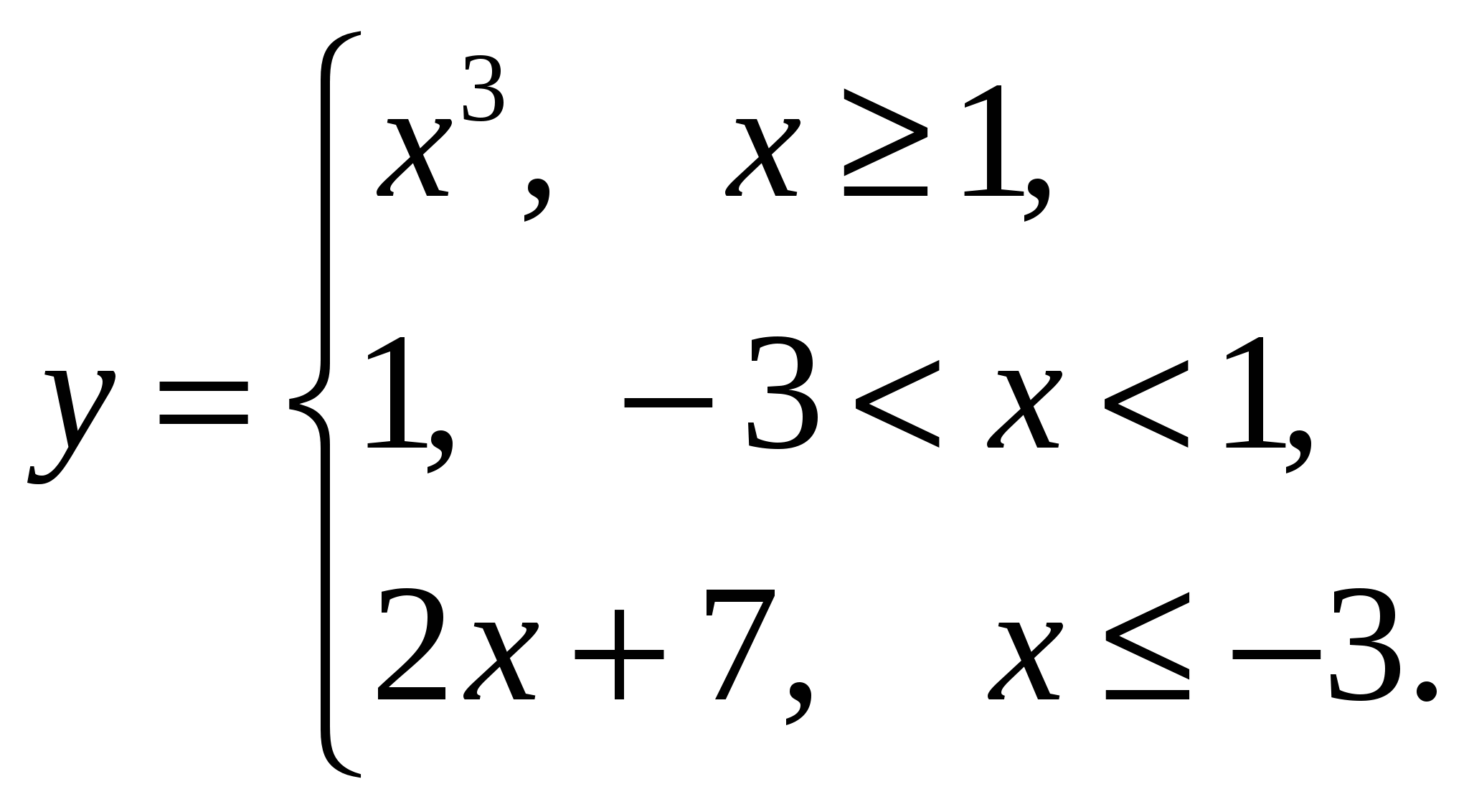
3. Актуализация знаний. (5 мин.)
1) Вычислить устно: ![]()
2) Вспомнить определение степени и расписать по определению следующие степени: ![]()
3) Записать в виде степени:
4. Новый материал. (10 мин.)
Приведенное выше задание, записать выражение в виде степени, надо выполнить несколькими способами. Например:
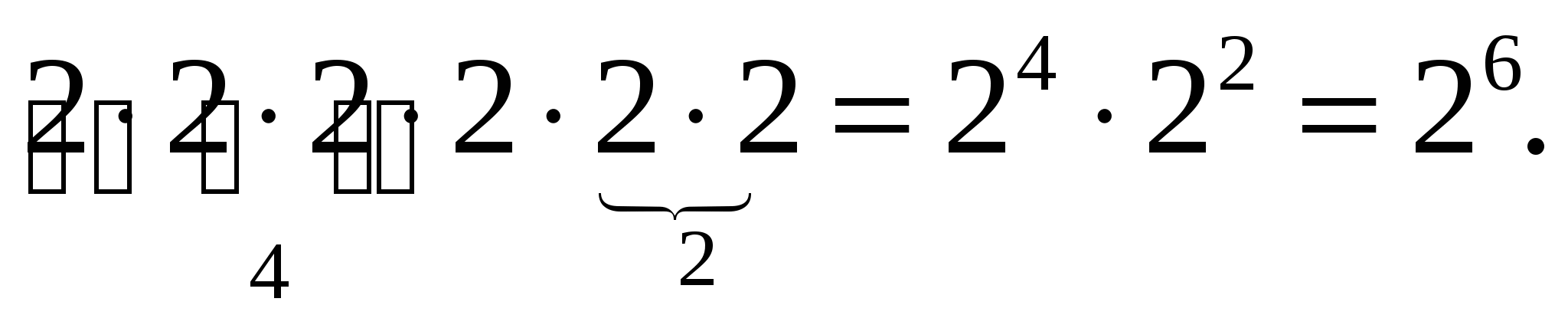
Выполнить все задания таким образом. После чего делается вывод о произведении степеней.
После этого преподаватель объясняет правило и доказывает формулу (в сильных классах).
Затем рассмотреть на доске следующий пример:
![]()
Попросить кого-нибудь из учеников аналогичным способом рассмотреть следующие примеры:
![]()
Затем делается вывод о частном степеней. Учитель объясняет правило и доказывает формулу.
5. Закрепление нового материала. (15 мин.)
Рассмотреть решение заданий № 617, 619, 626.
Для экономии времени номера выполняются не на доске, а под диктовку. Продиктовать хотя бы один пример должен каждый ученик.
На доске рассмотреть примеры № 625, 629 и 630.
6. Итоги урока. (3 мин.)
7. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 6.1.
Решить задания № 618, 621, 627.
Урок 64. Произведение и частное степеней
Тема: Произведение и частное степеней.
Цели урока: повторить и закрепить понятие степени, правила произведения и частного степеней; объяснить правила решения и оформления элементарных уравнений со степенями. В течение урока развивать у учеников навык упрощения произведения и частного степеней, навык решения элементарных уравнений со степенями.
Ход урока:
1. Организационный момент. (2 мин.)
2. Индивидуальный опрос. (8 мин.)
У доски четверо учеников выполняют задания по карточкам. Необходимо упростить выражения.
| Карточка 2.
| Карточка 3.
| Карточка 4.
|
Остальные ученики выполняют самостоятельно задания № 620 и 628. Сначала проверяется работа на доске, а затем устно проверяются номера в тетрадях.
3. Новый материал. (5 мин.)
Учитель показывает уравнение со степенями и дает возможность ученикам продумать решение. Затем объясняет или дополняет, если кто-нибудь из учеников решил, решение, а также показывает правила оформления таких уравнений. Для решения дается следующее уравнение: ![]() .
.
4. Закрепление нового материала. (25 мин.)
Рассмотреть решение № 622, 624, 634.
Так же выполняются задания № 623, 631, 632, 636 и 641.
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 6.1.
Решить задания № 633, 637, 640 и 650.
Урок 65. Степень степени
Тема: Степень степени.
Цели урока: повторить и закрепить понятие степени, правила произведения и частного степеней; объяснить правила возведения степени в степень. В течение урока развивать у учеников навык упрощения произведения и частного степеней, а так же возведение степени в степень.
Ход урока:
1. Организационный момент. (2 мин.)
2. Актуализация знаний. (15 мин.)
1) Самостоятельно ученики выполняют № 638 , проверяется устно.
2) Затем решаются задания № 642, 647, 648.
3. Новый материал. (8 мин.)
Учитель показывает пример: ![]() .
.
Аналогичным способом рассмотреть на доске: ![]() .
.
После чего делается вывод, каким образом легче возводить степень в степень. Затем преподаватель дает правило и формулу с доказательством.
4. Закрепление нового материала. (15 мин.)
1) Рассмотреть задания № 658, 659, 661 и 662.
2) Рассмотреть решение заданий повышенной трудности:
а) Представить сумму в виде степени с основанием 2 ![]()
б) Представить сумму в виде степени с основанием 3 ![]() .
.
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 6.2.
Решить задания № 646, 651, 657 и 660.
Урок 66. Степень произведения и дроби
Тема: Степень произведения и дроби.
Цели урока: повторить и закрепить понятие степени, правила произведения и частного степеней, правила возведения степени в степень; объяснить правила возведения произведения и частного в степень и правило вынесения множителя со степенью за скобки. В течение урока развивать у учеников навык упрощения произведения и частного степеней, возведение степени, произведения и частного в степень.
Ход урока:
1. Организационный момент. (2 мин.)
2. Актуализация знаний. (10 мин.)
1) Упростить следующие выражения:
![]()
![]()
![]()
![]()
2) Затем решаются задания № 650, 655, 663.
3. Новый материал. (8 мин.)
Преподаватель на доске показывает правила возведения произведения и частного в степень, записывает и доказывает формулу.
4. Закрепление нового материала. (20 мин.)
Рассмотреть задания № 666, 667, 669, 673 и 675.
Если времени достаточно, то предлагается рассмотреть задания повышенной трудности. Для выполнения данных заданий учитель должен заострить внимание детей на правилах вынесения множителя со степенью за скобки.
Упростить выражения:
а) ![]() б)
б) ![]()
в) ![]()
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 6.2.
Решить задания № 668, 672 и 674.
Урок 67. Степень произведения и дроби
Тема: Степень произведения и дроби.
Цели урока: повторить и закрепить свойства степеней; проверить знания и умения учеников по работе со степенями. В течение урока развивать у учеников навык упрощения выражений со степенями, решения уравнений со степенями, сравнения выражений со степенями.
Ход урока:
1. Организационный момент. (2 мин.)
2. Устная работа. (5 мин.)
На карточках или на доске приготовить выражения, которые ученики должны будут упростить.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Но учащиеся должны не только упростить выражения, но и объяснить какие правила для этого используются.
3. Актуализация знаний. (5 мин.)
На доске разбирается задание № 677.
4. Новый материал. (13 мин.)
Учитель показывает решение уравнений с применение изученных правил и разбирается № №649, 664, 687.
Так же преподаватель объяснение правил сравнения чисел со степенями, рассмотреть № 645 и 686.
5. Решение задач. (5 мин.)
Рассмотреть задание № 683.
6. Тестирование. (10 мин.)
Проверить знания учеников с помощью тестов, приготовленных на карточках для каждой парты.
Вариант 1.
1. Упростить выражение ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
2. Упростить выражение ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
3) Найти значение выражения ![]()
1) 64; 2) 8; 3) 16; 4) 12.
4) При каком значении переменной данное равенство является верным ![]() .
.
1) 8; 2) 3; 3) 4; 4) 6.
5) Из данных выражений выберете то, которое больше![]() .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
6) Упростите выражение ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
7) Вычислить ![]()
1) 26; 2) 44; 3) 134; 4) 116.
Вариант 2.
1. Упростить выражение ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
2. Упростить выражение ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
3) Найти значение выражения ![]()
1) 64; 2) 8; 3) 16; 4) 12.
4) При каком значении переменной данное равенство является верным ![]() .
.
1) 8; 2) 3; 3) 4; 4) 6.
5) Из данных выражений выберете то, которое меньше![]() .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
6) Упростите выражение ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
7) Вычислить ![]()
1) 26; 2) 44; 3) 134; 4) 116.
ОТВЕТЫ
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Вариант 1. | 2 | 2 | 3 | 1 | 1 | 4 | 1 |
| Вариант 2. | 1 | 4 | 1 | 2 | 4 | 3 | 3 |
7. Итоги урока. (3 мин.)
8. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 6.2.
Решить задания № 678, 682 и 685.
Тема: Решение комбинаторных задач.
Цели урока: повторить и закрепить свойства степеней; проверить знания и умения учеников по работе со степенями; объяснить понятие комбинаторных задач. В течение урока развивать у учеников навык решения комбинаторных задач.
Ход урока:
1. Организационный момент. (2 мин.)
2. Самостоятельная работа. (13 мин.)
| Вариант 2. | |
| 1) Упростить выражения: | |
| а) | а) |
| 2) Вычислить: | |
|
|
|
| 3) При каких значения | |
| а) б) | а) б) |
3. Новый материал. (5 мин.)
Учитель рассказывает о комбинаторных задачах. Так же преподаватель показывает правила решения и оформления задач на примере № 689.
4. Закрепление нового материала. (20 мин.)
Рассмотреть задачи № 690, 692, 694, 696 и 698.
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 6.3.
Решить задачи № 691, 693 и 695.
Урок 69. Перестановки
Тема: Перестановки.
Цели урока: повторить и закрепить понятие комбинаторных задач; проверить умение учеников решать комбинаторные задачи; объяснить понятие перестановок; ввести понятие факториала и объяснить правила работы с ним; рассмотреть задачу – шутку для повышения интереса к математике. В течение урока развивать у учеников навык решения комбинаторных задач и задач на перестановки.
Ход урока:
1. Организационный момент. (2 мин.)
2. Индивидуальный опрос. (10 мин.)
Четверо учеников выходят к доске для решения задач по карточкам. Трое работают самостоятельно, а четвертый – решает и объясняет задачу для класса. Затем разбираются остальные задачи. Ученики записывают в тетради все задачи.
| Карточка 2. Сколько будет всевозможных двузначных чисел из указанных цифр: 1, 2, 3, если в записи числа допускается повторение цифр? |
| Карточка 3. Сколько будет всевозможных двузначных чисел из указанных цифр: 1, 2, 3, используя в записи числа каждую из них не более одного раза. |
| Карточка 4. Сколько будет всевозможных двузначных чисел из указанных цифр: 0, 3, 4, если в записи числа допускается повторение цифр? |
3. Новый материал. (8 мин.)
Учитель рассказывает о перестановках. Вводится знак факториала, учитель показывает его обозначение и смысл. Так же преподаватель показывает правила решения и оформления задач на примере № 702.
4. Закрепление нового материала. (20 мин.)
Рассмотреть задачи № 704, 706, 707, 710 и 712.
Так же рассмотреть решение следующей задачи:
1) Бабушка на зиму закрутила каждого варения по одной банке: клубничное, абрикосовое, малиновое, вишневое, яблочное и клюквенное, и спрятала весь запас в шкаф. Петя нашел варенье еще до зимы и съел за пять дней 5 банок варенья. Когда бабушка заглянула в шкаф, то обнаружила только клюквенное варенье. Сколькими способами мог лакомиться Петя, если в день он съедал по одной банке варенья? Сильно ли расстроилась бабушка?
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 6.4.
Решить задачи № 703, 705, 709 и 711.
Урок 70. Подготовка к контрольной работе
Тема: Подготовка к контрольной работе.
Цели урока: повторить и закрепить правила работы со степенями, понятие комбинаторных задач и задач на перестановки. В течение урока развивать у учеников умение упрощать и вычислять выражения по правилам степеней, решать комбинаторные задачи и задачи на перестановки. Так же в течение урока в детях развивать чувства товарищества и сотрудничества.
Ход урока:
1. Организационный момент. (2 мин.)
Рассадить класс на пять групп. Сказать тему и задачи урока.
2. Актуализация знаний. (13 мин.)
1) Вспомнить свойства степеней по группам. Каждая группа должна объяснить одно из свойств степеней. Для объяснения надо рассказать правило данного свойства, записать и доказать формулу, привести примеры. Каждой группе задается по одному вопросу из вопросов для повторения на странице 187.
| 2. Гр. – 2 | 3. Гр. – 3 | 4. Гр. – 4 | 5. Гр. – 5 |
Группа сама определяет, кто из ее участников пойдет объяснять свой вопрос к доске. Остальные слушают и задают вопросы. Вопросы разбираются поочередно.
2) На карточках или на доске приготовить выражения для устного упрощения.
![]()
![]()
3. Решение задач. (25 мин.)
1) Все выполняют № 639, в группе решение может обсуждаться и объясняться. После истечения времени данного на решение, номер проверяется устно. Если какое-то задание хоть у кого-то неправильно, то его ученик из другой группы объясняет у доски.
2) Затем аналогичным способом решается № 679.
3) После этого учитель, по своему усмотрению, вызывает к доске по одному ученику с каждой группы. Этот ученик будет показывать знания всей группы. Для этого на каждую группу дается две карточки, в каждой карточке по одному примеру. У разных групп примеры разные, но на обеих карточках одной группы примеры одинаковые. Одна карточка дается ученику у доски, а вторая группе. Все приступают к выполнению задания.
| Задание 2
| Задание 3
| Задание 4
| Задание 5
|
Затем каждая группа проверяет своего участника. Если правильно, то вся группа поняла тему, если нет, то вызывается другой ученик из этой же группы для объяснения своего примера.
4) Затем каждой группе дается карточка с двумя задачами. Ученики должны решить задачи и все в группе должны их записать и понять. Затем с каждой группы вызывается к доске для оформления первой задачи на доске. Пока ученики с каждой группы записывают задачи на доске, устно проверяются вторые задачи. Задание должно быть прочитано и объяснено, каким образом оно решается, и сколько получилось в ответе. А после проверяются всем классом задачи на доске.
| Карточка 2.
|
| Карточка 3.
|
| Карточка 4.
|
| Карточка 5.
|
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Решить задания № 1 – 9 (стр. 188).
Урок 71. Контрольная работа
Тема: Контрольная работа.
Цели урока: проверить знания учеников по данной теме.
Ход урока:
1. Организационный момент.
2. Контрольная работа.
Вариант 1.
1. Упростите выражения:
а) ![]() б)
б) ![]() в)
в) 
2. Вычислите: а) ![]() б)
б) ![]()
3. Упростите выражение: а) ![]() б)
б) ![]()
4. Катя, Оля и Света договорились по очереди носить в школу словарь. Сколько у них есть способов установить порядок? Перечислите все возможные способы.
5. Верно ли, что: а) ![]() б)
б) ![]()
Вариант 2.
1. Упростите выражения:
а) ![]() б)
б) ![]() в)
в) 
2. Вычислите: а) ![]() б)
б) ![]()
3. Упростите выражение: а) ![]() б)
б) ![]()
4. В классе выдвинули четыре кандидатуры на пост президента класса и его заместителя: Миша, Гриша, Маша и Даша. Сколькими способами это можно сделать? Перечислите все возможные способы.
5. Верно ли, что: а) ![]() б)
б) ![]()
3. Домашнее задание.
Решить задания № 713 и 715.
Урок 72. Одночлены и многочлены
Тема: Одночлены и многочлены.
Цели урока: провести анализ контрольной работы и закрепить пройденный материал; объяснить понятия одночленов и многочленов. В течение урока развивать у учеников умение отличать одночленов от многочленов и приводить многочлены к стандартному виду.
Ход урока:
1. Организационный момент. (2 мин.)
2. Анализ контрольной работы. (8 мин.)
На доске разбираются задания из контрольной работы, при решении которых было допущено наибольшее количество ошибок. Так же для закрепления пройденного материала разобрать решение следующих заданий.
1) Упростить выражения:
а) ![]() б)
б) ![]()
2) Надя, поехав на неделю на море, взяла 7 платьев. Сколько способов у Нади поносить все платья, если каждое платье она будет одевать один раз на целый день.
3. Новый материал. (10 мин.)
На доске записаны следующие выражения:
![]()
![]()
Учащиеся по своему усмотрению делят данные буквенные выражения на одночлены и многочлены, записывая на доске в два разных столбика. Затем преподаватель говорит определение одночленов и их свойства, а ученики просматривают выражения, которые были разделены и ищут ошибки. Каждая ошибка должна быть объяснена. Затем по оставшимся буквенным выражениям ученики самостоятельно должны ввести понятие многочленов. Преподаватель только направляет их и упорядочивает ответы.
4. Закрепление нового материала. (20 мин.)
Устно разбираются задания № 717 и 719.
Письменно на доске и в тетрадях решаются задачи № 718, 720, 725, 728, 730 и 723 (самостоятельно по вариантам).
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 7.1.
Решить задания № 721, 722 и 727.
Урок 73. Сложение и вычитание многочленов
Тема: Сложение и вычитание многочленов.
Цели урока: повторить и закрепить понятия одночленов и многочленов; вспомнить правила раскрытия скобок и приведения подобных слагаемых; объяснить правила сложения и вычитания многочленов. В течение урока развивать у учеников умение складывать и вычитать многочлены.
Ход урока:
1. Организационный момент. (2 мин.)
2. Актуализация знаний. (13 мин.)
1) Опросить учащихся определения одночлена и многочлена, их свойства. Для заданных выражений устно перечислить все члены многочленов и указать коэффициенты членов, содержащих буквенные множители:
![]()
![]()
![]()
![]()
![]()
2) Прочитать данные многочлены по убыванию степени переменной:
![]()
![]()
![]()
3) На доске выполнить с полным объяснением задание № 729.
3. Новый материал. (5 мин.)
Сначала вспомнить правила раскрытия скобок, если перед скобкой стоят знаки плюс или минус, так же повторить определение подобных одночленов. А после к доске вызвать ученика, который самостоятельно, без помощи учителя, попробует сложить и вычесть данные многочлены: ![]() и
и ![]() . Затем совместными усилиями выводится правило сложения и вычитания многочленов.
. Затем совместными усилиями выводится правило сложения и вычитания многочленов.
4. Закрепление нового материала. (20 мин.)
Решить задания № 736, 739, 742, 744, 745 и 747.
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 7.2.
Решить задания № 737, 740 и 746.
Урок 74. Сложение и вычитание многочленов
Тема: Сложение и вычитание многочленов.
Цели урока: повторить и закрепить понятия одночленов и многочленов, правила сложения и вычитание многочленов; проверить умение учеников приводить многочлены к стандартному виду. В течение урока развивать у учеников умение складывать и вычитать многочлены, упрощать выражения.
Ход урока:
1. Организационный момент. (2 мин.)
2. Индивидуальная работа. (8 мин.)
К доске вызывается четыре ученика, для выполнения заданий по карточка. Кроме письменного выполнения, требуется еще умение объяснить по правилам ход действий.
| Карточка 2. Упростить:
| |
| Карточка 3. Упростить:
| Карточка 4. Упростить:
|
В момент выполнения заданий на доске преподаватель проводит фронтальный опрос по определениям и правилам данной темы. Затем проверяется правильность заданий и еще раз проговариваются правила, но теперь те ученики, которые выполняли задания.
3. Актуализация знаний. (10 мин.)
Закрепить правила при решении на доске задания № 726, 734 и 743. Если у кого-нибудь из учеников возникают проблемы, учитель еще раз объясняет у доски.
4. Решение задач. (20 мин.)
Разобрать задание № 749. Затем преподаватель объясняет, как многочлен представить суммой или разность и решаются примеры № 750, 751, 753, 755.
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 7.2.
Решить задания № 738, 741 и 757.
Урок 75. Умножение одночлена на многочлен
Тема: Умножение одночлена на многочлен.
Цели урока: повторить и закрепить понятия одночленов и многочленов, правила сложения и вычитания многочленов; объяснить правило умножения одночлена на многочлен. В течение урока развивать у учеников умение умножать одночлен на многочлен.
Ход урока:
1. Организационный момент. (2 мин.)
2. Актуализация знаний. (8 мин.)
Устно разобрать задание № 748, при этом вспомнить правила, помогающие выполнить это упражнение. Затем разобрать задание № 752.
3. Устная работа. (5 мин.)
Раскрыть скобки в выражения (приготовить или на карточках или на доске):
![]()
Вспомнить название свойства, при помощи которого раскрывались скобки, а затем и правило, выражающее это свойство.
4. Новый материал. (5 мин.)
Предложить ученикам самостоятельно найти произведение ![]() . Обсудить этот пример и совместными усилиями вывести правило умножения одночленов на многочлены. Если ученикам тяжело выполнять умножение, то вводится понятие «фонтанчик». «Фонтанчик» идет от одночлена к каждому члену многочлена.
. Обсудить этот пример и совместными усилиями вывести правило умножения одночленов на многочлены. Если ученикам тяжело выполнять умножение, то вводится понятие «фонтанчик». «Фонтанчик» идет от одночлена к каждому члену многочлена.
5. Закрепление нового материала. (20 мин.)
1) Рассмотреть задания № 764, 766, 771 и 767.
2) Так же умножить данный одночлен ![]() на каждый из многочленов, в данном задании происходит постепенное усложнение произведения:
на каждый из многочленов, в данном задании происходит постепенное усложнение произведения:
а) ![]() б)
б) ![]() в)
в) ![]()
г) ![]() д)
д) ![]()
3) Вспомнить правила решения уравнений со знаменателями:
а) ![]() б)
б) ![]()
6. Итоги урока. (3 мин.)
7. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 7.3.
Решить задания № 765, 768 и 770.
Урок 76. Умножение одночлена на многочлен
Тема: Умножение одночлена на многочлен.
Цели урока: повторить и закрепить понятия одночленов и многочленов, правила сложения и вычитания многочленов, правило умножения одночлена на многочлен; проверить знания и умения учащихся, по данной теме. В течение урока развивать у учеников умение складывать и вычитать многочлены, умножать одночлены на многочлены.
Ход урока:
1. Организационный момент. (2 мин.)
2. Актуализация знаний. (8 мин.)
На доске упростить следующие выражения:
При выполнении вспомнить и повторить все правила по теме.
3. Самостоятельная работа. (30 мин.)
| Вариант 2. | |
| № 724(а), 731, 733(а, в), 754(а, в), 772(а, в). | № 724(б), 732, 733(б, г), 754(б, г), 772(б, г). |
Дополнительно для сильных учеников ительно мо
4. Итоги урока. (3 мин.)
5. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 7.3.
Решить задания № 756 и 775.
Урок 77. Умножение одночлена на многочлен
Тема: Умножение одночлена на многочлен.
Цели урока: повторить и закрепить правила сложения и вычитания многочленов, правило умножения одночлена на многочлен; рассмотреть решение задачи – шутки для развития у детей интереса к математике. В течение урока развивать у учеников умение складывать и вычитать многочлены, умножать одночлены на многочлены.
Ход урока:
1. Организационный момент. (2 мин.)
2. Анализ самостоятельной работы. (3 мин.)
Выставить оценки и разобрать задания из работы, которые при решении вызвали затруднения.
3. Актуализация знаний. (12 мин.)
Вспомнить и закрепить сложение и вычитание многочленов, упростить следующие выражения:
Вспомнить закрепить умножение одночлена на многочлен, выполнить задание № 769.
4. Решение задач. (25 мин.)
1) Рассмотреть задания № 773, 774(б), 776(б), 777, 778(б), 779.
2) Решить уравнение ![]()
3) Степа получил по математике двойку. Папа, узнав об этом, 15 минут бегал за Степой с ремнем, а Степа убегал со скоростью ![]() метров в секунду. Потом папа схватился за сердце и сев в кресло, стал ждать маму. Когда пришла мама, Степе пришлось скорость своего бега увеличить на 2 метра в секунду, но у мамы силы иссякли за 6 минут. Сколько метров пришлось бегать Степе от своих разгневанных родителей?
метров в секунду. Потом папа схватился за сердце и сев в кресло, стал ждать маму. Когда пришла мама, Степе пришлось скорость своего бега увеличить на 2 метра в секунду, но у мамы силы иссякли за 6 минут. Сколько метров пришлось бегать Степе от своих разгневанных родителей?
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 7.3.
Решить задания № 774(а), 776(а) и 778(б, в).
Урок 78. Умножение многочлена на многочлен
Тема: Умножение многочлена на многочлен.
Цели урока: повторить и закрепить правила умножения одночлена на многочлен; объяснить правила умножения многочленов. В течение урока развивать у учеников умение умножать одночлены на многочлены, находить произведение многочленов.
Ход урока:
1. Организационный момент. (2 мин.)
2. Устная работа. (5 мин.)
Найти произведения:
![]()
![]()
3. Новый материал. (13 мин.)
Учитель объясняет правило умножения многочленов, показывает на доске примеры выполнения:
![]()
![]()
Для упрощения показывается «фонтанчик».
4. Закрепление нового материала. (20 мин.)
1) Рассмотреть задания № 781, 783 и 784.
2) Так же умножить данный многочлен ![]() на каждый из многочленов, в данном задании происходит постепенное усложнение произведения:
на каждый из многочленов, в данном задании происходит постепенное усложнение произведения:
а) ![]() б)
б) ![]() в)
в) ![]()
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 7.4.
Решить задания № 780 и 785.
Урок 79. Умножение многочлена на многочлен
Тема: Умножение многочлена на многочлен.
Цели урока: повторить и закрепить правила умножения одночлена на многочлен, умножение многочленов; проверить умение учеников находить произведение многочленов. В течение урока развивать у учеников умение находить произведение многочленов.
Ход урока:
1. Организационный момент. (2 мин.)
2. Индивидуальная работа. (8 мин.)
Четверо учеников выходят к доске для работы с карточками.
| Карточка 2. Выполнить умножение:
| |
| Карточка 3. Выполнить умножение:
| Карточка 4. Выполнить умножение:
|
Остальные ученики выполняют задание № 787.
Сначала учащиеся проверяют правильность примеров на доске, а затем у доски рассматривается примеры № 787.
3. Актуализация знаний. (10 мин.)
Найти произведение следующих выражений:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Лучше, если кто-то из учеников будет работать у доски: записать пример, закрыть от класса доску и решить, затем доска открывается и пример проверяется. У каждого ребенка будет возможность проверить себя.
4. Решение задач. (10 мин.)
Рассмотреть задание № 786.
5. Самостоятельная работа. (10 мин.)
| Вариант 2. | |
| Найти данные произведения: | |
| 1) 2) 3) 4) 5) | 1) 2) 3) 4) 5) |
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 7.4.
Решить задания № 782 и 791.
Урок 80. Умножение многочлена на многочлен
Тема: Умножение многочлена на многочлен.
Цели урока: повторить и закрепить правила выполнения действий между одночленами и многочленами. В течение урока развивать у учеников умение упрощать выражения с одночленами и многочленами, использовать свои знания для выполнения разных видов заданий; так же развивается чувство сотрудничества и сопереживания.
Ход урока:
1. Организационный момент. (2 мин.)
Рассадить детей на 5 групп. Рассказать тему урока и задачи урока.
2. Анализ самостоятельной работы. (5 мин.)
Выставить оценки и разобрать задания из работы, которые при решении вызвали затруднения. Так же проводится фронтальный опрос всего класса по определения и правилам.
-
Что называется одночленом?
-
Что называется многочленом?
-
Какие слагаемые являются подобными?
-
Что такое стандартный вид одночлена? многочлена?
-
Влияет ли коэффициент на подобия слагаемых?
-
Что значит сложить подобные слагаемые?
-
Расскажите правило раскрытия скобок, если перед скобкой знак плюс.
-
Если перед скобкой знак минус.
-
Если перед скобкой множитель.
-
Расскажите правило умножения многочленов.
3. Актуализация знаний. (13 мин.)
На столе преподавателя лежат три стопки карточек. В первой карточки с выражениями одночленов:
![]()
Во второй и третьей карточки с выражениями многочленов:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
В каждой стопке по шесть карточек. Из каждой группы выходит по очереди по одному ученику и для своей группы берет по карточке из каждой стопки. И с данными выражениями группа должна выполнить следующие упражнения:
-
Умножить одночлен на многочлен.
-
Сложить многочлены.
-
Из первого многочлена вычесть второй.
-
Умножить многочлен на многочлен.
Примеры записываются и решаются. Примеры должны быть записаны у каждого в группе и решение должен уметь объяснить каждый из группы.
После выполнения задания, учитель из каждой группы вызывает по одному ученику. Этот ученик должен записать примеры на доске и затем объяснить решение. Пока задания записываются, остальные устно выполняют и разбирают задание № 796.
4. Решение задач. (13 + 7 мин.)
1) После каждой группе выдается карточка с выражениями для упрощения. Карточки у всех одинаковые. Учащиеся должны обсудить в группе, каким образом выполнять действия и внимательно решить.
После выполнения устно проверяются ответы. Каждая группа читает по одному ответу. Если в каком-нибудь примере возникли трудности, то пример обсуждается на доске. (Обратить внимание на пятый пример.)
2) Затем каждой группе раздается по карточке с заданием на доказательство. Если ученики не могут справиться, преподаватель чуть-чуть должен подсказать.
| Карточка 2. Докажите, что значение выражения не зависит от переменной
|
| Карточка 3. Докажите, что при всех целых
|
| Карточка 4. Докажите, что при всех целых
|
| Карточка 5. Докажите, что при всех натуральных |
Каждая задача показывается и обсуждается у доски.
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 7.4.
Решить задание № 789.
Урок 81. Умножение многочлена на многочлен
Тема: Умножение многочлена на многочлен.
Цели урока: повторить и закрепить правила выполнения действий с одночленами и многочленами; рассмотреть решение заданий на данную тему повышенной трудности; проверить знания учеников по упрощению выражений, содержащих одночлены и многочлены. В течение урока развивать у учеников умение упрощать выражения с одночленами и многочленами, умение использовать свои знания.
Ход урока:
1. Организационный момент. (2 мин.)
2. Актуализация знаний. (10 мин.)
Вспомнить и повторить все правила, необходимые для упрощения выражений. Выполнить на доске, с полным объяснением номер № 788.
3. Решение задач. (18 мин.)
Рассмотреть усложненные задания на данную тему.
1) Докажите, что при всех натуральных ![]() , больших 2, значение выражения делится на 12:
, больших 2, значение выражения делится на 12: ![]() .
.
2) Представить в виде многочлена выражение ![]()
3) Рассмотреть задания № 792, 794, 795(а, в).
4. Самостоятельная работа. (10 мин.)
| Вариант 2. | |
| Упростить выражения: | |
| 1) 2) 3) 4) 5) | 1) 2) 3) 4) 5) |
5. Итоги урока. (3 мин.)
6. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 7.4.
Решить задания № 793 и 798.
Урок 82. Формулы квадрата суммы и разности
Тема: Формулы квадрата суммы и разности.
Цели урока: повторить и закрепить правила выполнения действий с одночленами и многочленами; вывести и доказать формулы квадрата суммы и разности; показать применение данных формул. В течение урока развивать у учеников умение пользоваться формулами сокращенного умножения.
Ход урока:
1. Организационный момент. (2 мин.)
2. Анализ самостоятельной работы. (5 мин.)
Провести анализ самостоятельной работы. Для закрепления пройденной темы упростить следующие выражения:
а) ![]()
б) ![]()
3. Актуализация знаний. (10 мин.)
Запишите степень двучлена в виде произведения и выполните умножение:
![]()
![]()
4. Новый материал. (8 мин.)
Сделать с учениками вывод, после которого отдельно выписываются формулы квадрата суммы и разности на плакат, с заголовком «Формулы сокращенного умножения». Затем по формуле записать правила, которые помогут правильно читать данные выражения.
5. Закрепление нового материала. (15 мин.)
Рассмотреть задания №799, 801, 803, 806.
Так же с использованием данных формул вычислить значения выражений, предварительно упростив их:
а) ![]() б)
б) ![]()
6. Итоги урока. (3 мин.)
7. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 7.5.
Решить № 800 и 804.
Здесь представлен конспект к уроку на тему «Обыкновенные и десятичные дроби 7 Класс», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (7 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

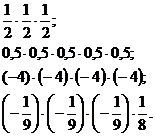
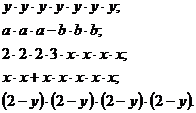
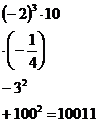
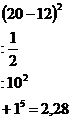
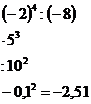
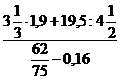
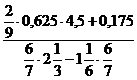
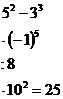
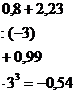
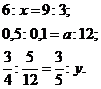
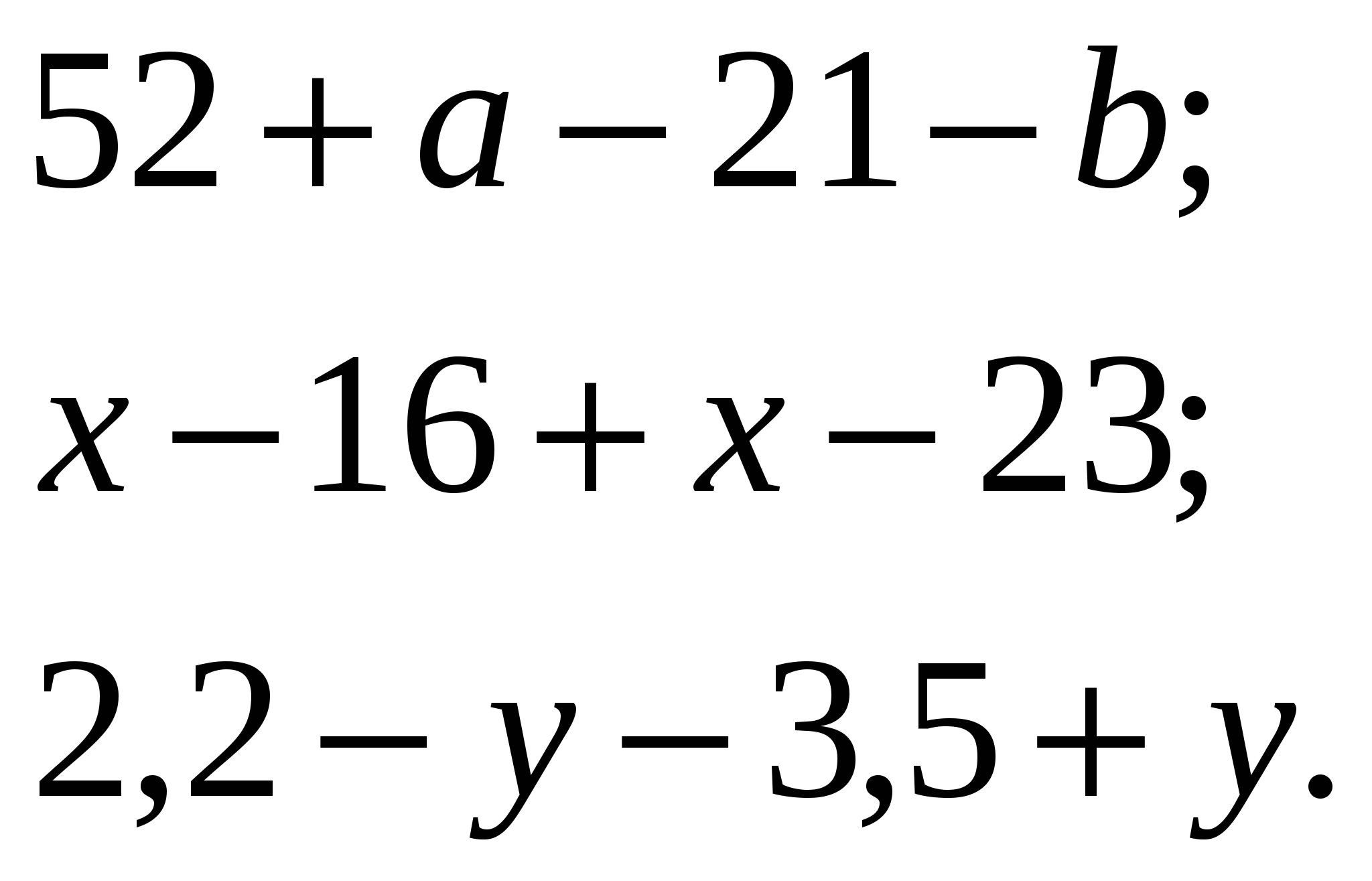
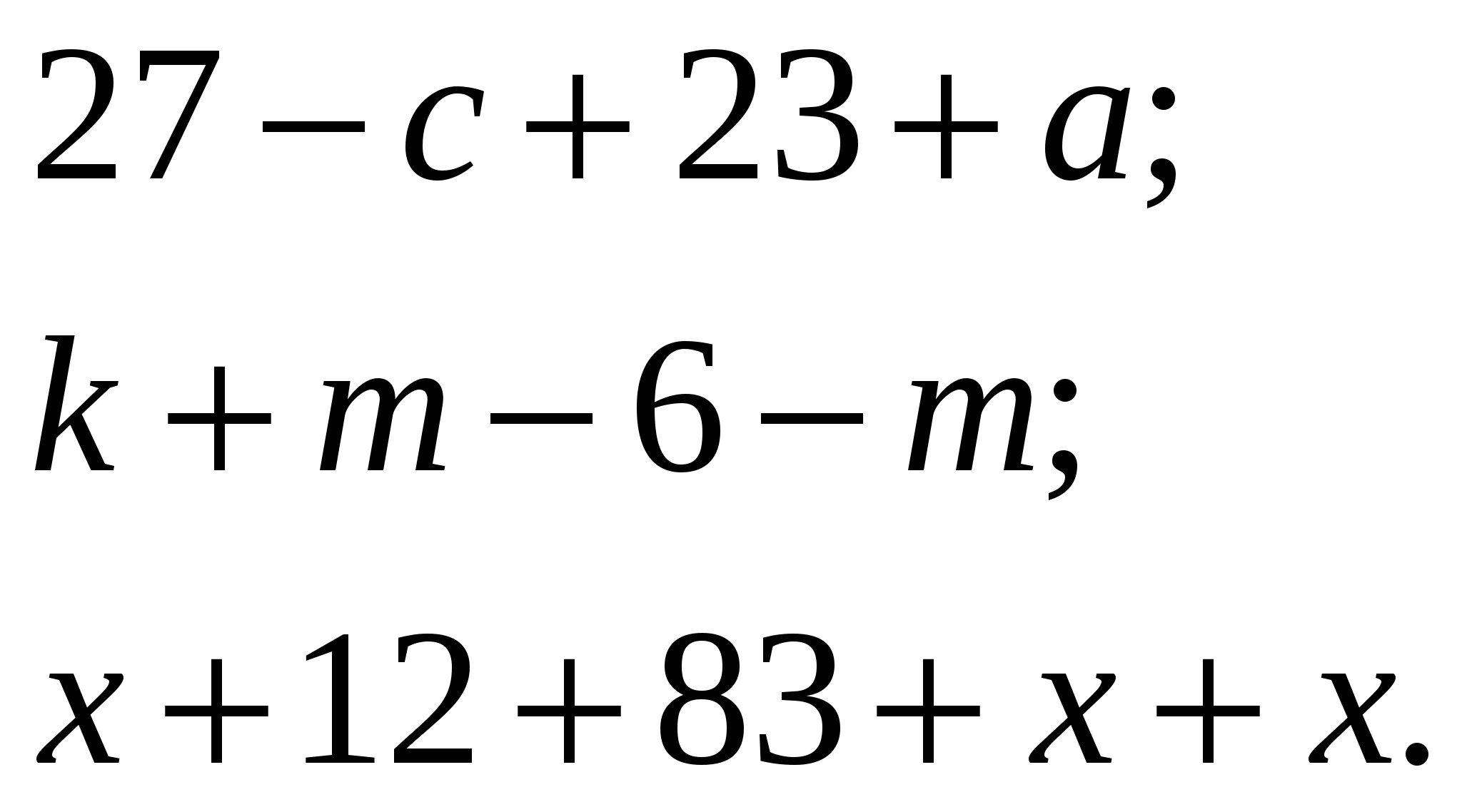
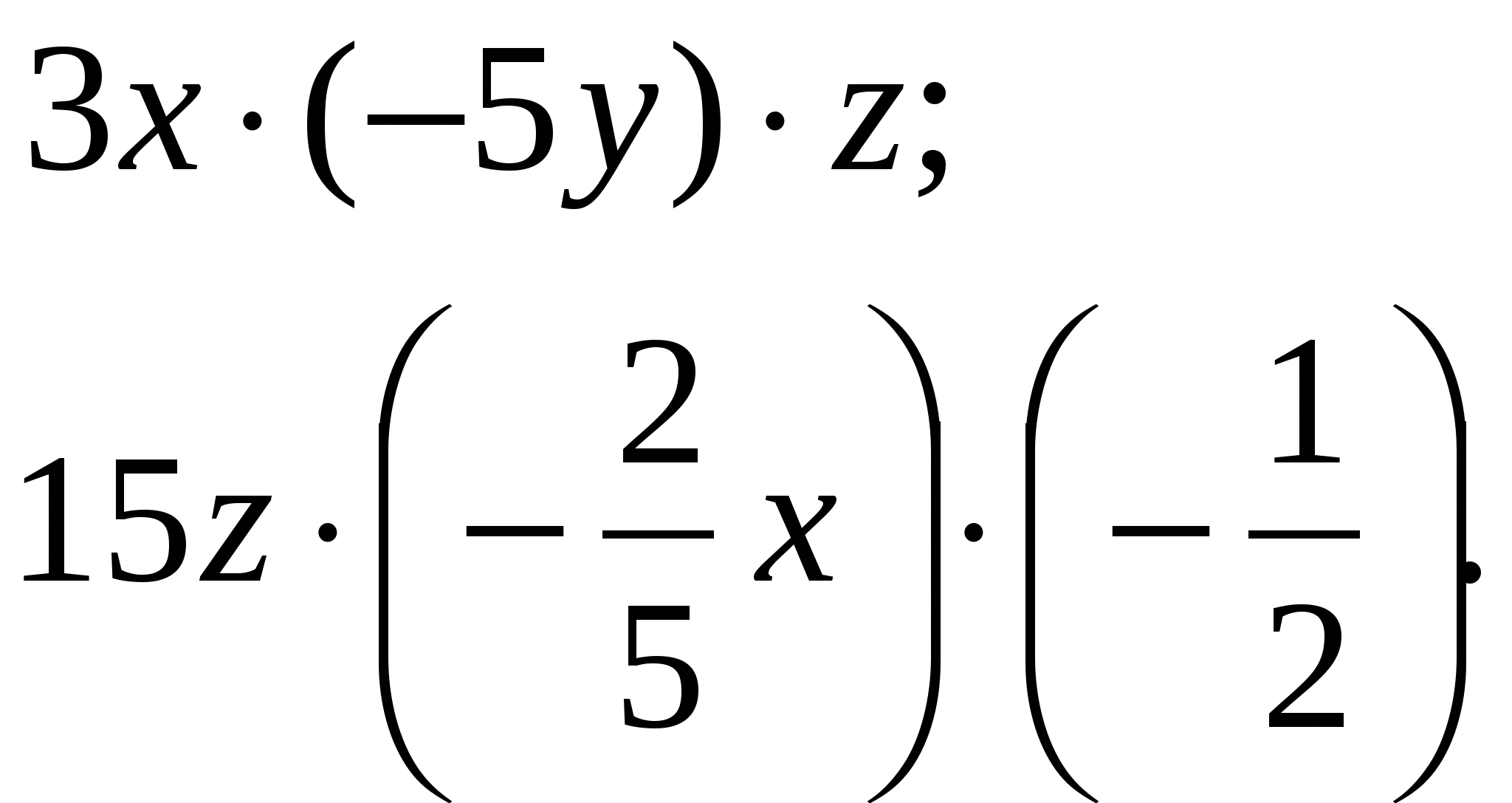
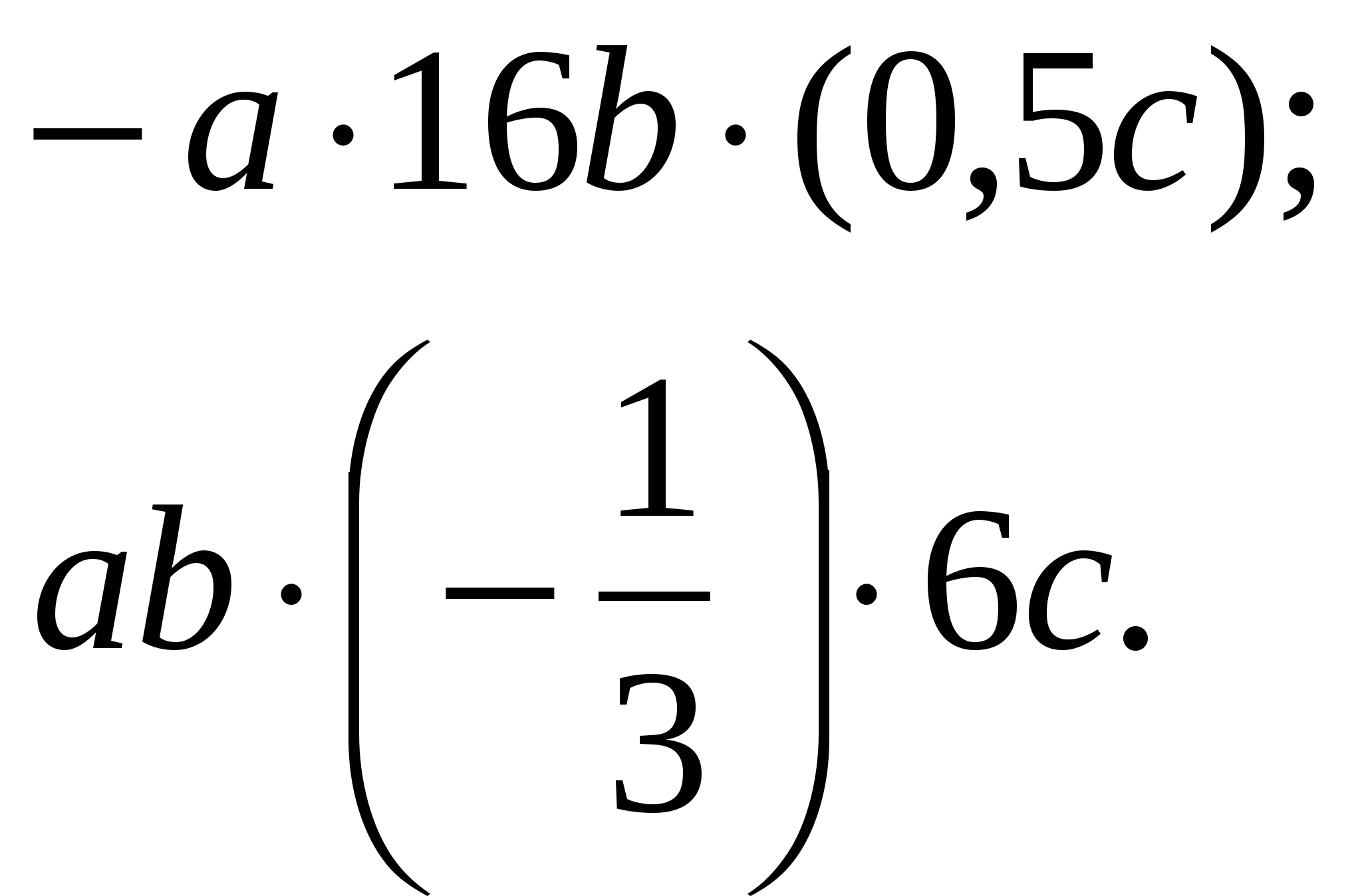
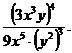
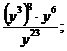 б)
б)