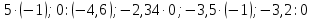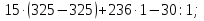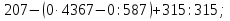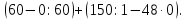Дидактические цели элементов урока

Содержание урока, формы взаимодействия с учащимися

Мотивационная беседа с учащимися (1 мин.)

Обратить внимание учащихся на актуальность темы, необходимость полного усвоения темы для дальнейшего обучения, прикладной значимости. Сообщить цель урока.

Рассказ учителя. Компьютерная презентация.

Сообщаю тему урока, эпиграф урока.

– Здравствуйте, ребята! Каждый новый день, тем более весенний - повод для радости, интересных встреч и удивительных открытий. Вы знаете, у меня сегодня чудесное настроение, такое же яркое, доброе, как солнышко на небе и на ваших партах, потому что мне приятно видеть вас таких умных, любопытных, старательных, в общем - замечательных. Девизом нашего урока сегодня пусть будут такие слова, прочитаем их хором… «Математику мы любим. Обещаем не болтать, а серьезно думать, мыслить и всё правильно решать!» (Слайды 1, 2)

Актуализация опорных знаний

(5 мин.)

Обеспечение мотивации и принятия учащимися цели, учебно-познавательной деятельности, актуализация опорных знаний и умений. Готовность учащихся к активной учебно-познавательной деятельности на основе опорных знаний.

Устный счет.

Ни костяшек, ни ручек, ни мела-

Устный счет. Мы творим это дело,

Только силой ума и души!

Числа сходятся где-то во тьме,

И глаза начинают светиться!

И кругом серьезные лица.

Устный счет! Мы считаем в уме!

1. Выполните действия: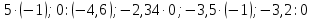

- Какое выражение не имеет смысла? Почему?

2. Кто быстрее?

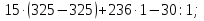
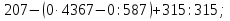
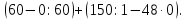
3. Ребусы.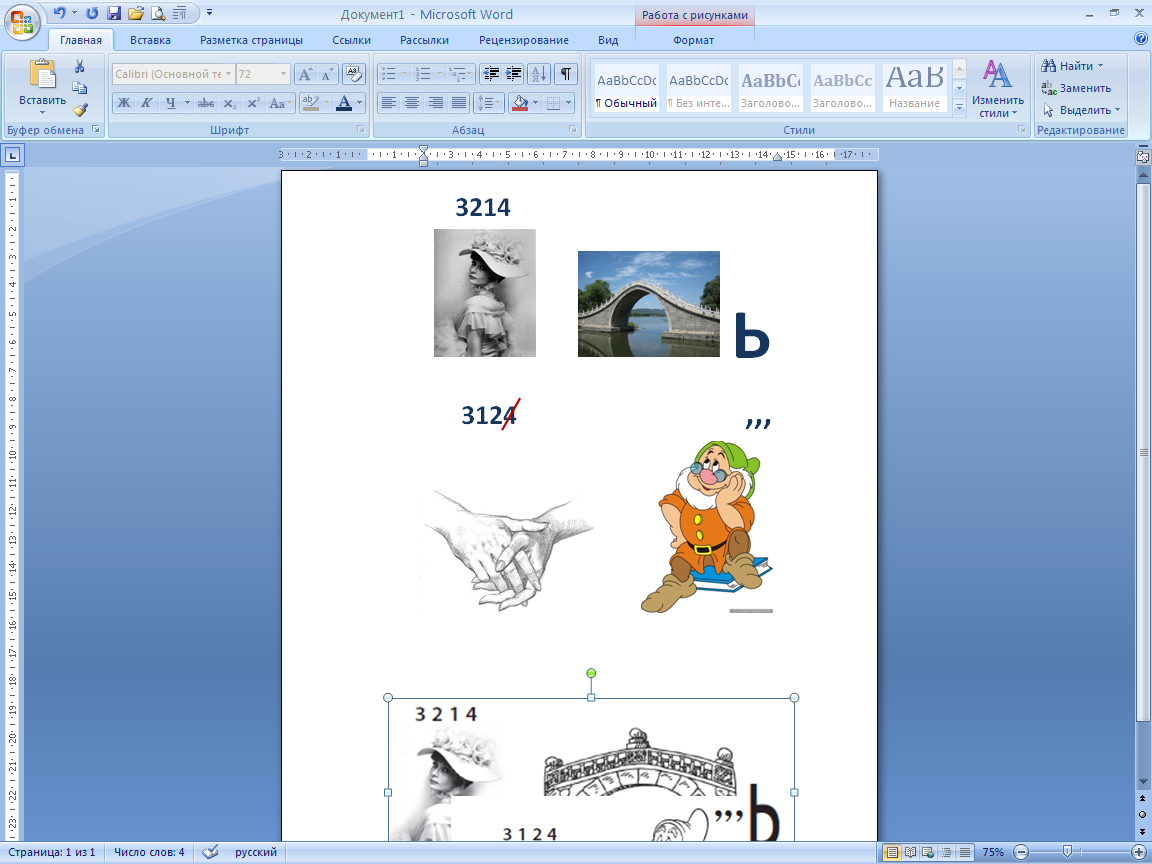

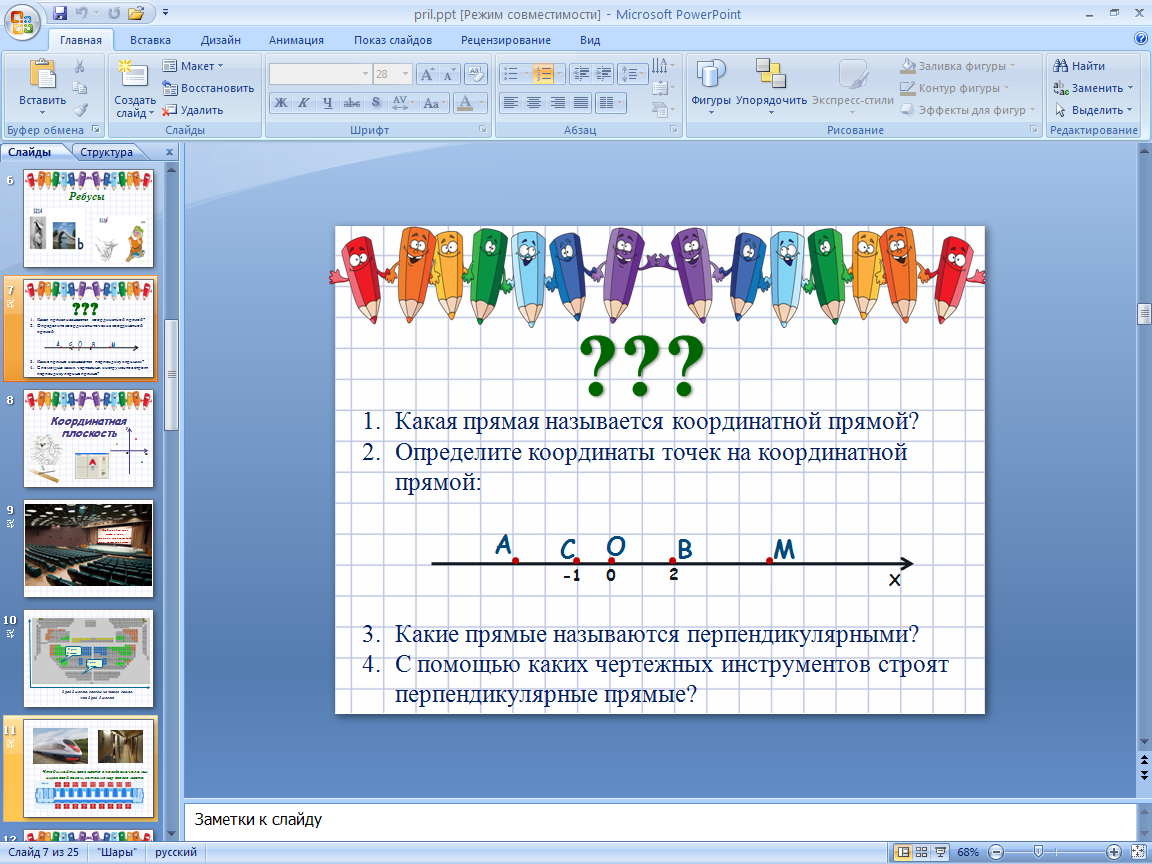
4. Ответьте на вопросы???

• Какая прямая называется координатной прямой?

• Определите координаты точек, отмеченных на координатной прямой:

• Какие прямые называются перпендикулярными?

• С помощью каких чертежных инструментов строят перпендикулярные прямые? (Слайды 3, 4,5, 6, 7)

Усвоение содержания учебного материала

(18 мин.)

Обеспечение восприятия осмысления и первичного запоминания знаний и способов действий, связей и отношений в объекте изучения.

– Общаясь друг с другом, люди часто говорят: "Оставьте свои координаты". Для чего? Чтобы человека было легко найти. Это могут быть: номер телефона, домашний адрес, место работы, Е-mail. Главное здесь в том, что по этим данным человека можно будет найти. Именно в этом и состоит суть координат или, как обычно говорят, системы координат: это правило, по которому определяется положение того или иного объекта. Кроме почтовых адресов и номеров телефонов системы координат пронизывают всю практическую жизнь человека. Кто из вас хотя бы раз не был в кинотеатре? Таких нет. Что нужно знать, чтобы найти свое место в зале? А кто из вас хоть раз не ездил на поезде? Таких тоже нет. Чтобы найти свое место в поезде сначала мы ищем свой вагон, затем номер своего места. (Слайды 8,9, 10, 11)

Более чем за 100 лет до н.э. греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами. Чтобы определить местонахождение объекта по карте нужно знать его координаты. Также систему координат можно проследить при игре в шахматы и морской бой. В игру “Морской бой” играют на 100-клеточной доске или на бумаге в клеточку, рисуя таблицу 10 х 10. Каждая клетка на игровом поле определяется буквой и цифрой. Буквами помечены горизонтали игрового поля, а цифрами – вертикали. Аналогичная система координат используется и в шахматах, только горизонтали на шахматной доске всегда обозначают латинскими буквами. Такого рода “клеточные координаты” обычно используются на военных, морских, геологических картах. Применяются они и на туристических схемах городов для облегчения поиска нужной улицы или какой-либо достопримечательности. (Слайды 12, 13, 14, 15)

Идея координат зародилась ещё в древности. Первоначальное их применение связано с астрономией и географией, с потребностью определить положение светил на небе и объектов на поверхности Земли. Уже во II в. древнегреческий астроном Клавдий Птоломей пользовался широтой и долготой в качестве координат. Общематематическое значение метода координат открыли французские математики XVII в. Пьер Ферма и Рене Декарт. В 1637 году Рене Декарт впервые опубликовал изложение метода координат, поэтому прямоугольную систему координат называют также —«Декартова система координат».

Термины «абсцисса» и «ордината» (образованные от латинских слов «отсекаемый» и «упорядоченный») были введены в 70-80 гг. XVII в. немецким математиком Вильгельмом Лейбницем. Итак, вы уже, наверное, догадались, что для того, чтобы определить положение какой-либо точки на плоскости необходимо знать две ее координаты. (Слайды 16, 17)

Возникает вопрос: “А как же все-таки определить положение точки на плоскости?” Для этого на плоскости строят две перпендикулярные прямые (обычно одну из них располагают горизонтально, а другую – вертикально) и вводят на каждой из них обычные координаты. Эти координаты согласованны между собой. Точка пересечения прямых О называется началом координат. Эта буква выбрана не случайно, а по сходству написания с цифрой 0 или как первая буква латинского слова origo – начало. Сами координатные прямые называют осями координат. Горизонтальную ось называют осью абсцисс (или осью Х), вертикальную ось называют осью ординат (или осью Y). Плоскость, на которой задана система координат, называется координатной плоскостью, которая разделяется осями абсцисс и ординат на четверти. Посмотрим, как определяется положение точки на координатной плоскости.

(Слайды 18, 19, 20, 21)

Устно решим задание из учебника № 1394, № 1395.

Решим на доске и в тетрадях: № 1393, № 1399

(Слайд 22)

Физкультминутка (2 мин.)

Снять утомление учащихся, повысить умственную работоспособность учащихся.

Читается стихотворение, а дети выполняют действия.

Раз, два – стоит ракета. (Руки вытянуты вверх.)

Три, четыре – самолет. (Руки в стороны.)

Раз, два – хлопок в ладоши, (Хлопаем в ладоши над головой.)

А потом на каждый счет.

Раз, два, три, четыре - (Четыре хлопка перед собой.)

Руки выше, (Руки вверх, потянуться.)

Плечи шире. (Руки в стороны, предплечья вверх.)

Раз, два, три, четыре (Ходьба на месте.)

И на месте походили.

А сейчас мы с вами, дети,

Улетаем на ракете. (Руки вверх, ладони соединить – «купол ракеты».)

На носочки поднялись

Быстро, быстро руки вниз.

Обеспечение осознанности формируемых знаний

(8 мин.)

Самостоятельное выполнение заданий, требующих применения знаний в знакомой и измененной ситуации.

Работа в парах с электронным практикумом по теме «Координатная плоскость» (учащиеся работают за ноутбуками, выполняя построение рисунков по точкам с заданными координатами) (Слайд 23)

Подведение итогов

(2 мин.)

Дать анализ и оценку успешности достижения цели и наметить перспективу последующей работы. Получение учащимися информации о реальных результатах учения.

• Под каким углом пересекаются координатные прямые Х и У?

• Как называют каждую из этих прямых?

• Как называют точку пересечения этих прямых?

• Сколько чисел нужно знать, чтобы задать положение точки на координатной плоскости?

• Как называют пару чисел, определяющих положение точки на плоскости?

• Как называют первое число?

• Как называют второе число?

Рефлексия (2 мин.)

Усвоение принципов саморегуляции и сотрудничества. Открытость учащихся в осмыслении своих действий и самооценке.

Надеюсь, что вы этот материал не забудете, и мы в дальнейшем будем часто его использовать. А теперь пусть каждый из вас ответит на вопросы:

На уроке мне …

1. Было интересно…

2. Я научился…

3. Было трудно…

4. Меня удивило…

5. Мне захотелось…

(Учащимся предлагается выбрать фигуру, которая, по их мнению, соответствует его настроению на уроке: , ,) (Слайд 24)

Выставление отметок

(1 мин.)

Сообщить учащимся отметки, полученные во время урока.

Домашнее задание

(1 мин.)

Обеспечение понимания цели, содержания и способов выполнения домашнего задания. Проверка соответствующих записей.

Учащимся предлагается домашнее задание либо П45. № 1417; 1418, 1419, либо творческое задание: придумать и построить по координатам рисунок.

(Слайды 25)