Конспект урока «Формулы сокращенного умножения. Квадрат суммы» по математике

Тема: Формулы сокращенного умножения. Квадрат суммы.

Форма урока: урок формирования и совершенствования знаний.

Вид урока – комбинированный.

Цель урока: 1) дидактическая – показать учащимся формулу, её доказательство и способы применения. Закрепить использование формулы.

2) логическая – упражнять учащихся в анализе, сравнении, обобщении.

3) воспитательная – привить интерес к изучаемой теме.

План урока:

1) Повторить понятия, связанные с одночленами и многочленами.

2) , 3) Познакомить учащихся с формулой квадрата суммы.

4) Выделить основные типы задач, где используется формула.

5) , 6) Закрепить и обобщить пройденный материал.

7) Задать домашнее задание.

1 этап. Актуализация знаний.

На этот урок было задано Д./З.: повторить такие понятия, как одночлен, стандартный вид

одночлена, коэффициент одночлена, многочлен, стандартный вид многочлена, подобные слагаемые, приведение подобных слагаемых.

На доске написаны одночлены и многочлены.

1) x² + x; 2) –2aba; 3) 10x – 8xz – 3xz; 4) –bca; 5) 25ab + ab² + a²b; 6) ; 7) zz6; 8) 25a⁸4b;

9) (–f²)² ; 10) x⁶ – 10; 11) a²c – 9aca + 6; 12) a

Фронтальный опрос:

• Определение одночлена: Одночлен – произведение чисел, переменных и их степеней, а также числа, переменные и степени.

Назвать пункты, в которых записаны одночлены. Ответ: 2), 4), 6), 7), 8), 9), 12)

• Определение стандартного вида одночлена: Стандартный вид одночлена – произведение числового множителя, стоящего на первом месте и степеней различных переменных.

Назвать пункты, в которых записаны одночлены в стандартном виде. Ответ: 4), 6), 12)

• Определение коэффициента одночлена: Коэффициент одночлена – числовой множитель одночлена, записанного в стандартном виде.

Назвать коэффициент одночлена. Ответ: –2, –1, , 6, 100, 1, 1

• Определение многочлена: Многочлен – ( алгебраическая ) сумма одночленов.

Назвать пункты, в которых записаны многочлены. Ответ: 1), 3), 5), 10), 11)

• Определение стандартного вида многочлена: Стандартный вид многочлена – многочлен, в котором все одночлены записаны в стандартном виде и нет подобных слагаемых.

Назвать пункты, в которых многочлены записаны в стандартном виде. Ответ: 1), 5), 10)

• Определение подобных слагаемых: Подобные слагаемые ( члены ) – слагаемые, у которых

одинаковая буквенная часть.

Назвать подобные слагаемые. Ответ: a²c и – 9aca; – 8xz и – 3 xz;

• Определение приведения подобных слагаемых: Приведение подобных слагаемых –

преобразование, основанное на распределительном свойстве умножения

Привести подобные слагаемые. Ответ: - 8a²c; -11xz

2 этап: Мотивация знаний.

Задание на 5 мин в тетради для теории.

№ 1 . Упростить выражение:

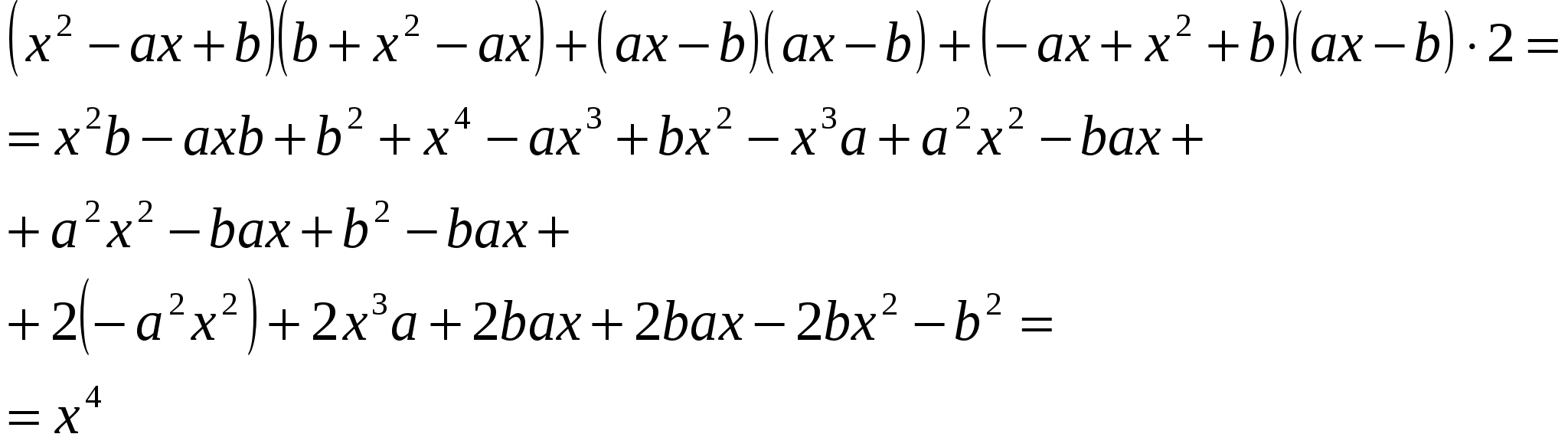
Спросить учащихся, какие ответы у них получились. Сделать вывод: что они работали 5 мин, а многие сделали не верно (не успели сделать). Вычисление занимает очень много времени.

А для упрощения работы существуют специальные формулы:

формулы сокращенного умножения

(отметить слово сокращенного ).

3 этап: Изложение нового материала.

В тетради для теории:

ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ.

Квадрат суммы.

( a + b )² = a² + 2ab + b²

 ( a + b )² = ( a + b )( a + b ) = a² + ab + ab + b² = a² + 2ab + b²

Вспомнить определение степени числа (произведение числа а само на себя n-ое количество раз).

Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.

(спросить нескольких учеников и повторить всем классом хором)

4 этап. Практическое применение формулы.

Использование этих формул:

1) Вычислить:

а) (30 + 1)² = 30² + 2301 + 1² = 900 + 60 + 1 = 961

б) 72² = (70 + 2)² = 70² + 270 2 + 2² = 4900 + 280 + 4 = 5184

в) 157² + 215743 + 43² = (157 + 43)² = 200² = 40000

2) Решение уравнений:

25x² + 20x + 4 = 0

(5x + 2)² =0

(5x + 2)(5x + 2) =0

5x + 2 = 0

x = -0,4

Ответ: {-0,4}

3) Представить выражение в виде многочлена:

(x² + 10)² = (x²)² + 2x²10 + 10² = x⁴ + 20x² + 100

4) Разложить многочлен на множители (определение: представить в виде произведения одночлена и многочленов или произведения многочленов):

a²+ 6ab + 9b = a² + 2a3b + (3b)²= (a + 3b)²

5) Вернуться к выражению, которое они упрощали в начале урока:

= (x² – ax + b + ax – b)² = (x²)² = x⁴

Обратить внимание, как быстро и легко упростили это выражение с помощью формулы квадрата суммы

Заметить, что в формуле вместо a и b могут быть числа, одночлены, многочлены и их комбинации.

5 этап. Решение задач.

Ученикам раздаются карточки с заданием. Решение и анализ проводится вместе с учителем.

Задание: Вместо многоточия поставить одночлен так, чтобы равенство выполнялось.

1. (a + 2b)² = a² + 4ab + 4b²,

2. (3x + a)² = 9x² + 6ax + a²,

3. (10 + 2a)²= 100 + 40a + 4a² ,

4. (6a² + 9c)² = 36a⁴ + 108a²c + 81c²,

5. (15a + 0,4c³ )² = 225a² + 12ac³ + 0,16c⁶,

6. (3a + 2,5b)² = 9a² + 6,25b² + 15ab ,

7. (3b + 2a)² = 9b² + 12ab + 4a²,

8. (3x + 7z )² = 9x² + 42xz + 49z²

Лист с решением вклеить в рабочую тетрадь.

6 этап: Обобщение знаний.

Повторить формулу; что может быть записано вместо переменных а и b ; ее чтение; способы использования.

7 этап: Домашнее задание.

Формула квадрата суммы. Учебник: Алимов 7 класс: № 371 (2, 3); № 378 (2 , 4); № 388 (2)