Конспект урока «Необычные способы умножения» по математике для 6 класса

Муниципальное казенное образовательное учреждение

Королевская средняя общеобразовательная школа

Тюменцевского района Алтайского края

Необычные способы умножения

Выполнила: Бондаренко Анастасия, ученица 6 класса МКОУ Королевской сош

Руководитель: Ладыгина Светлана Алексеевна, учитель математики МКОУ Королевской сош

пос. Королевский, 2015

Содержание

Введение

«Счет и вычисления – 
основа порядка в голове» 
Иоганн Генрих Песталоцци (1746 - 1827) 

Можно ли представить мир без чисел? Без чисел ни покупки не сделаешь, ни времени не узнаешь, ни номера телефона не наберёшь. А космические корабли, лазеры и все другие технические достижения?! Они были бы попросту невозможны, если бы не наука о числах.

Две стихии господствуют в математике — числа и фигуры с их бесконечным многообразием свойств и действий с ними.

Человеку в повседневной жизни невозможно обойтись без вычислений. Поэтому на уроках математики, нас в первую очередь учат выполнять действия над числами, то есть считать. Умножаем, делим, складываем и вычитаем мы привычными для всех способами, которые изучаются в школе.

Мне стало интересно, а есть ли еще какие-нибудь способы вычислений? Оказалось, что можно умножать не только так, как предлагают нам в учебниках математики, но и по-другому. Используя интернет-ресурсы, я узнала много необычных способов умножений.

Цель работы: изучить нестандартные приёмы умножения и показать, что их применение делает процесс вычисления рациональным и интересным.

Задачи:

• изучить историю возникновения счета;

• найти как можно больше необычных способов вычислений;

• описать некоторые способы умножения и опытным путём выявить трудности их использования;

Методы:

• анализ исторических сведений о возникновении чисел и счётных устройств;

• знакомство со старинными способами умножения.

I. История счёта

1.1. Как люди научились считать

Число - одно из основных понятий математики - родилось в глубокой древности в связи с практической необходимостью. Сначала люди «на глаз» сравнивали разные количества одинаковых предметов. Они могли определить в какой из двух куч больше плодов, в каком стаде больше оленей и т.д.

Затем в человеческом языке появились числительные и люди смогли называть число предметов, животных, дней. Таких числительных было мало и их число зависело от подсчитываемых предметов. Одно и тоже число называли разными словами, если, например, считали людей, рыб, лодки, сети, звёзды, палки. Мы и сейчас используем разные неопределённые числительные со значением «много»: «толпа», «стадо», «стая», «куча», «пучок» и другие.

С развитием производства и торгового обмена люди стали понимать, что общего у трёх лодок и трёх топоров, десяти стрел и десяти орехов. Племена часто вели обмен «предмет на предмет». Например, обменивали 5 съедобных кореньев на 5 рыб. Становилось ясно, что 5 — одно и тоже число и для кореньев и для рыб. Значит, и называть их можно одним словом.

Постепенно люди начали использовать для счёта камешки, палочки, части собственного тела. Вот как известный учёный Н.Н. Миклухо-Маклай описывает счёт папуасов: «Папуас загибает один за другим пальцы рук, причём издаёт определённый звук, например, «бе, бе, бе». Досчитав до 5, он говорит «Ибон - бе» (рука). Затем он загибает пальцы другой руки, снова повторяет «бе, бе...» пока не дойдёт до «ибон - али» (две руки). Затем он идёт дальше, приговаривая «бе, бе, ...» и восклицает «самба - бе» (одна нога) и «самба - али» (две ноги). Если нужно считать дальше, папуас пользуется пальцами рук и ног кого-нибудь другого». Руки и ноги — это первый инструмент для счёта.(1)

А как записывали числа? До возникновения письменности использовали зарубки на палках, насечки на костях, узелки на верёвках. Найденная волчья кость в Дольни-Вестонице (Чехословакия) имела 55 насечек, сделанных 25000 лет назад.(1)

За несколько столетий до новой эры изобрели способ записи чисел, при котором цифрами служили буквы обычного алфавита. Такой алфавитной нумерацией пользовались до XVII века. Чтобы отличить «настоящие» буквы от чисел, над буквами-числами ставили чёрточку (на Руси эта чёрточка называлась «титло»). Тогда не было единой позиционной системы во всех нумерациях и поэтому было очень трудно выполнять действия.

Изобретение индийцами десятичной позиционной нумерации в 6 веке считается одним из крупнейших достижений человечества. Индийская нумерация и индийские цифры стали известны в Европе от арабов и обычно их называют арабскими.

1.2.Счётные устройства

Математики во все времена мечтали о таких помощниках, которые освободили бы их из плена долгих и утомительных вычислений. И такие устройства стали изобретать.

Одним из первых вычислительных устройств был АБАК (от греческого слова «abax» - доска). Эта счётная рама появилась в 5 веке до н.э., а пользовались ею до XVIII века. Известны несколько разновидностей абака: греческий, римский, китайский, японский и другие. Русский абак - это счёты, они появились в 16 веке и иногда ими пользуются ещё и в наши дни.

За абаками были созданы АРИФМОМЕТРЫ. Они были сконструированы независимо друг от друга разными изобретателями: итальянцем Леонардо да Винчи (XV век), немецким учёным В. Шиккардом (XVII век), французским математиком Блез Паскалем (XVII век) и другими.

Арифмометры — это настольная механическая вычислительная машина для выполнения четырёх математических действий. Русский арифмометр был сконструирован инженером Одиером в 1874 году.

Долгое время популярным счётным устройством была ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА, изобретённая лондонским профессором Гунтером в 1625 году. Служила она до XX века и была вытеснена микрокалькуляторами.

Первую программно-управляемую вычислительную машину создал английский учёный Ч.Беббидж в XVIII веке. Первую электронно-вычислительную машину «ЭНИАК» разработали в США в 1945 году.

Первая отечественная ЭВМ была разработана в 1947 году под руководством академика С.А. Лебедева. С его именем связано дальнейшее развитие российской вычислительной техники.

Современный помощник вычислений – микрокалькулятор - прибор, позволяющий производить сложные вычисления за короткий промежуток времени. Микрокалькуляторы удобны в эксплуатации: лёгкие, размеры их невелики. Их часто можно встретить встроенными в часы, мобильные телефоны. Но, несмотря уже на имеющиеся удобства, процесс развития вычислительной техники продолжается.

1.3. «Чудо — счётчики»

Встречаются люди с необыкновенными способностями, которые по быстроте устных вычислений могут состязаться с ЭВМ. Их называют «чудо – счётчиками». И таких людей немало.

Рассказывают, что отец Гаусса, рассчитываясь со своими рабочими в конце недели, прибавлял оплату к каждому дневному заработку за сверхурочные часы. Однажды, после того как Гаусс-отец закончил расчёты, следивший за операциями отца ребёнок, которому было 3 года, воскликнул: «Папа, подсчёт не верен! Вот такая должна быть сумма!» Вычисления повторили и с удивлением убедились, что мальчик указал правильную сумму.

Мадмуазель Осака-японка, англичанин Бакстон, американец Фаллер и другие производили в уме быстро и точно сложнейшие вычисления.

В Грузии живёт Арон Чикашвили. Как-то друзья решили проверить его возможности «чудо-счётчика». Его попросили сосчитать, сколько слов и букв скажет диктор, комментирующий второй тайм футбольного матча. Одновременно был включен магнитофон. Ответ последовал, как только диктор сказал последнее слово: 17427 букв и 1835 слов. На проверку ушло 5 часов, ответ оказался правильным.

Проводились соревнования ЭВМ и человека в институте кибернетики Украинской академии наук. В соревновании участвовал молодой счётчик-феномен Игорь Шелушков и ЗВМ «Мир». Машина за несколько секунд сделала множество сложных операций, но победителем оказался Игорь Шелушков.

В Сиднейском университете в Индии тоже проходили соревнования человека и машины. Шакунтала Деви тоже опередила ЭВМ.

Большинство таких людей обладает прекрасной памятью и имеют дарование. Но некоторые из них никакими особыми способностями к математике не обладают. Они знают секрет! А секрет этот в том, что они усвоили приёмы быстрого счёта, запомнили несколько специальных формул. Значит, и мы тоже можем, пользуясь этими приёмами, быстро и точно считать.

II Старинные способы умножения

2.1. Умножение на 9

Растопырьте пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки (это изображено на рисунке).

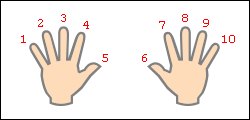
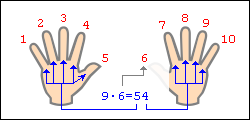
Допустим, хотим умножить 9 на 6. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 6. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа - количество единиц. Слева у нас 5 пальцев не загнуто, справа - 4 пальца. Таким образом, 9·6=54. Ниже на рисунке детально показан весь принцип "вычисления".

2.2. Индийский способ умножения.

Самый ценный вклад в сокровищницу математических знаний был совершен в Индии. Индусы предложили употребляемый нами способ записи чисел при помощи десяти знаков: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.

Основа этого способа заключается в идее, что одна и та же цифра обозначает единицы, десятки, сотни или тысячи, в зависимости от того, какое место эта цифра занимает. Занимаемое место, в случае отсутствия каких – нибудь разрядов, определяется нулями, приписываемыми к цифрам.

Индусы отлично считали. Они придумали очень простой способ умножения. Они умножение выполняли, начиная со старшего разряда, и записывали неполные произведения как раз над множимым, поразрядно. При этом сразу был виден старший разряд полного произведения и, кроме того, исключался пропуск какой-либо цифры. Знак умножения еще не был известен, поэтому между множителями они оставляли небольшое расстояние. Например, умножим их способом 537 на 6:

537 6 (5 ∙ 6 = 30)

(3 ∙ 6 = 18)

(7 ∙ 6 = 42)

30 + 18 + 42 3222

2.3. Умножение чисел методом «ревность»

Сначала рисуется прямоугольник, разделённый на квадраты, причём размеры сторон прямоугольника соответствуют числу десятичных знаков у множимого и множителя. Затем квадратные клетки, делятся по диагонали, и «…получается картинка, похожая на решётчатые ставни-жалюзи, - пишет Пачоли. – Такие ставни вешались на окна венецианских домов, мешая уличным прохожим видеть, сидящих у окон дам и монахинь».

Умножим этим способом 347 на 29. Начертим таблицу, запишем над ней число 347, а справа число 29.

В каждую строчку запишем произведение цифр, стоящих над этой клеткой и справа от нее, при этом цифру десятков произведения напишем над косой чертой, а цифру единиц – под ней. Теперь складываем числа в каждой косой полосе, выполняя эту операцию, справа налево. Если сумма окажется меньше 10, то ее пишем под нижней цифрой полосы. Если же она окажется больше, чем 10, то пишем только цифру единиц суммы, а цифру десятков прибавляем к следующей сумме. В результате получаем искомое произведение 10063.

3 4 7

2

9

10 0 6 3

Мы рассмотрели простой пример, однако, этим способом можно умножать любые многозначные числа.

Неудобства этого способа заключаются в трудоёмкости построения прямоугольной таблицы, а сам процесс умножения интересен и заполнение таблицы напоминает игру.

2.4. Крестьянский способ умножения.

Самым, на мой взгляд, легким способом умножения является способ, который употребляли русские крестьяне. Этот прием вообще не требует знания таблицы умножения дальше числа 2. Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа. Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат.

В случае нечетного числа надо откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением. Умножим 37 на 32

37……….32

74……….16

148……….8

296……….4

592……….2

1184……….1

Произведение всех пар соответственных чисел одинаковое, поэтому

37 ∙ 32 = 1184 ∙ 1 = 1184

В случае, когда одно из чисел нечетное или оба числа нечетные, поступаем следующим образом:

24……. 17

24…….16

48……. 8

96…….4

192…….2

384 ….…1

24 ∙ 17 = 24∙(16+1)=24 ∙ 16 + 24 = 384 + 24 = 408

2.5. Новый способ умножения

Интересен новый способ умножения, о котором недавно появились сообщения. Изобретатель новой системы устного счёта кандидат философских наук Василий Оконешников утверждает, что человек способен запоминать огромный запас информации, главное – как эту информацию расположить. По мнению самого учёного, наиболее выигрышной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе.

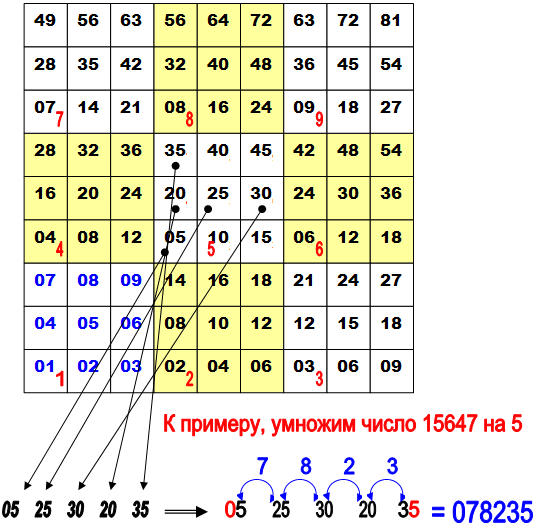
Считать по такой таблице очень просто. К примеру, умножим число 15647 на 5. В части таблицы, соответствующей пятёрке, выбираем числа, соответствующие цифрам числа по порядку: единице, пятёрке, шестёрке, четвёрке и семёрке. Получаем: 05 25 30 20 35

Левую цифру (в нашем примере - ноль) оставляем без изменений, а следующие цифры складываем попарно: пятёрку с двойкой, пятёрку с тройкой, ноль с двойкой, ноль с тройкой. Последняя цифра также без изменений.

В итоге получаем: 078235. Число 78235 и есть результат умножения.

Если же при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется на «своё» место.

Заключение

Нам известно высказывание древнегреческого математика, философа, жившего в IV веке до н.э.- Пифагора: «Всё есть число!». Согласно мнению этого учёного и его последователей, числа управляют не только мерой и весом, но также всеми явлениями в природе, и являются сущностью гармонии, царствующей в мире.

Научившись считать всеми представленными способами, я пришла к выводу: что самые простые способы это те, которые мы изучаем в школе, может быть они для нас более привычны.

Из всех найденных мною необычных способов счета более интересным показался способ умножение методом «ревность».

Самым простым мне показался метод «удвоения и раздвоения», который использовали русские крестьяне, очень удобно его использовать при умножении двузначных чисел.

Заинтересовал меня новый способ умножения, потому что он позволяет в уме «ворочать» огромными числами.

Старинные и современные способы вычислений показывают, что как в прошлом, так и в будущем, без математики, науки, созданной разумом человека, не обойтись.

Список литературы

1. Гейзер Г.И. История математики в школе, VII-VII классы. Пособие для учителя. - М.: Просвещение, 1982

2. http://matsievsky. newmail. ru/sys-schi/file15.htm