Конспект урока «Приложения производной и первообразной в механике» по математике

Интегрированный урок математики и физики

Приложения производной и первообразной в механике.

«Математика - царица всех наук, но

служанка физики»

Авторы: Орлова Е.В. – учитель математики МАОУ «СОШ №6» г.Перми;

Михайлина Н.В. – преподаватель физики ГБОУ СПО «Пермский

строительный колледж» г. Пермь.

Продолжительность 45 мин.

Цель:

• сформировать у учащихся умение применять математический аппарат к решению задач по физике;

• развивать мыслительные способности учащихся, умение анализировать, выделять общие и отличительные свойства; умений применять теоретические знания на практике;

• воспитывать устойчивый интерес к изучению математики и физики через реализацию межпредметных связей.

Оборудование:

• Компьютер;

• Мультимедийный проектор;

• Справочный материал по физике;

• Раздаточный материал с задачами.

Ход урока.

1. Организационный момент

Учитель математики: Математика - это инструмент для описания удивительно разнообразного множества явлений и предметов Вселенной. Поэтому она универсальна, она как бы стоит над всеми науками. Не зря знаменитый немецкий ученый Карл Фридрих Гаусс сказал: «Математика – царица всех наук». ( слайд 2). Но в то же время, она послушно обслуживает всевозможные науки, в частности физику. Поэтому говорят, что «Математика - царица всех наук, но служанка физики».( слайд 3).

Сегодня мы будем использовать математику как «служанку физики». Тема нашего урока «Приложения производной и первообразной в механике». ( слайд 4). Нам предстоит сравнить два подхода, к решению задач: традиционный – который вы используйте на уроках физики и «математический» - с использованием методов математического анализа.

Для того чтобы успешно справиться с задачами нам надо повторить ряд вопросов.

2. Актуализация опорных знаний

1. Определение производной;

2. Механический смысл производной (слайд 5 );

3. Найдите скорость и ускорение точки, движущейся прямолинейно по закону s(t) = 2t³ – 3t в момент времени t=1. (слайд6);

4. Движение точки происходит по закону x(t) = 2t² – 5t (x – в метрах, t – в секундах). Найдите скорость движения точки в момент t = 10 с. (слайд 7);

5. Скорость прямолинейного движения точки изменяется по закону v(t) = t² – 8t + 2. Найдите закон движения точки. (слайд 8);

6. Определение первообразной;

7. Найдите путь пройденный точкой за первые 5 с, если скорость точки изменяется по закону v(t) = 10 – 2t (t – время в секундах, v – скорость в метрах в секунду. (слайд 9);

8. В процессе урока нам могут понадобиться формулы, которые содержатся в справочном материале по физике.

Справочный материал по физике.

Законы движения.

х = х₀ + v₀t + at²/2

s = v₀t + at²/2

v = v₀ + at

Второй закон Ньютона

F=ma

Кинетическая энергия

E = mv²/2

Работа при деформации

А = /2

Переходим к решению задач.

3. Решение задач (фронтальная работа с классом. Решение задач записывается на доске и в тетрадях).

Задача 1. Тело массой 2 кг движется прямолинейно по закону х(t)=t²+t+1 (х - в метрах, t - в секундах). Найдите действующую силу и кинетическую энергию тела через 2 с после начала движения. (слайд 10).

Сила, действующая на тело в соответствии со вторым законом Ньютона вычисляется по формуле F = ma. Значит, для нахождения силы нам потребуется вычислить ускорение. Для этого ещё раз вспомним, каков механический смысл производной. (“Производная от координаты по времени - есть скорость. Производная скорости по времени - ускорение ”)

1. v(t) = x'(t)=2t + 1

a(t) = v'(t) =2 м/с² => F=22 = 4 H

2. E = mv²/2

v(t) = 2t + 1

v(2) = 5 м/с => E = 25 Дж

Учитель физики: А теперь давайте решим эту задачу другим способом.

х(t)=t²+t+1 F=ma (2 закон Ньютона)

t=2c E = mv²/2 (кинетическая энергия)

m=2кг х(t) = х₀+v₀t+at²/2 (закон движения)

F=? х(t) = 1+ t+ t²

Е=? х₀ = 1м

v₀ = 1м/с

а = 2 м/с²

F = 22 = 4H

v = v₀+at

v =1+2t

v = 5 м/с

E = 25²/2 = 25Дж

Вопрос к классу: какое решение короче? Какое проще?

Задача 2. Точка движется прямолинейно под действием постоянной силы с ускорением 2м/с². Начальная скорость равна нулю. Через 3 секунды после начала движения сила прекращает действовать и точка начинает двигаться равномерно с набранной скоростью. Найдите закон движения точки. (слайд 11).

а = 2 м/с² 1. х(t) = х₀+v₀t+at²/2 (закон движения)

v₀ = 0 х₀ = 0

t=3c v₀ = 0

х₁(t) = ? х₁(t) =t²

х₂(t) = ? 2. х₂(t) = х₀+v₀t+at²/2 (закон движения)

а = 0, т.к. движение равномерное.

v = v₀+at

v₀ = 0, => v = at, => v = 23 = 6 м/с

х₀ = s = v₀t+at²/2

х₀ = s = at²/2

х₀ = s = 23²/2=9м

х₂(t) = 9+6t

Учитель математики: Постараемся решить эту задачу средствами матанализа

1. a(t) =2.

Скорость точки будем находить из множества первообразных функции a(t): v(t) = 2t + C

Учитывая, что v(0) = 0, получим C = 0, а значит v(t) = 2t.

Используя понятие первообразной найдем x(t) = t² + C.

Учитывая, что x(0) = 0, получим C = 0, а значит x(t) = t², при t≤3

2. Через 3с v(t) = 6, x(t) =9 => на втором участке x(t) =6t + C

В момент начала равномерного движения (t = 0) x = 9.

Значит C = 0. Получим x(t) = 6t + C, при t > 3.

Сравните решения задачи. Для себя сделайте выбор какой способ удобнее.

Задача 3. Найдите работу, которую необходимо затратить на растяжение пружины на 5 см, если сила в 4 Н растягивает её на 10 см. (слайд 12).

Из курса физики вы знаете, что работой A силы называют произведение модуля силы и перемещения: A = FS.

Е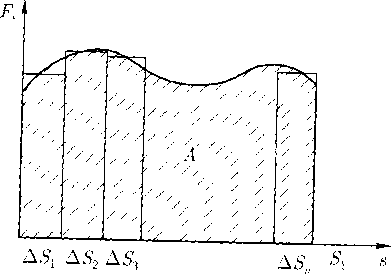сли на тело действует переменная сила, то чтобы вычислить её работу нужно перемещение разбить на малые участки ΔS, в пределах которых силу можно считать постоянной. Затем следует подсчитать работу на каждом таком участке и сложить все полученные результаты. Это и будет работа силы на интересующем нас перемещении.

Графический (слайд ) работу на каждом участке ΔS можно вычислить как площадь прямоугольника со сторонами ΔS и F(S). Тогда работа произведенная силой на перемещении S определяется как площадь криволинейной трапеции, находящейся под графиком проекции силы. Итак,

A =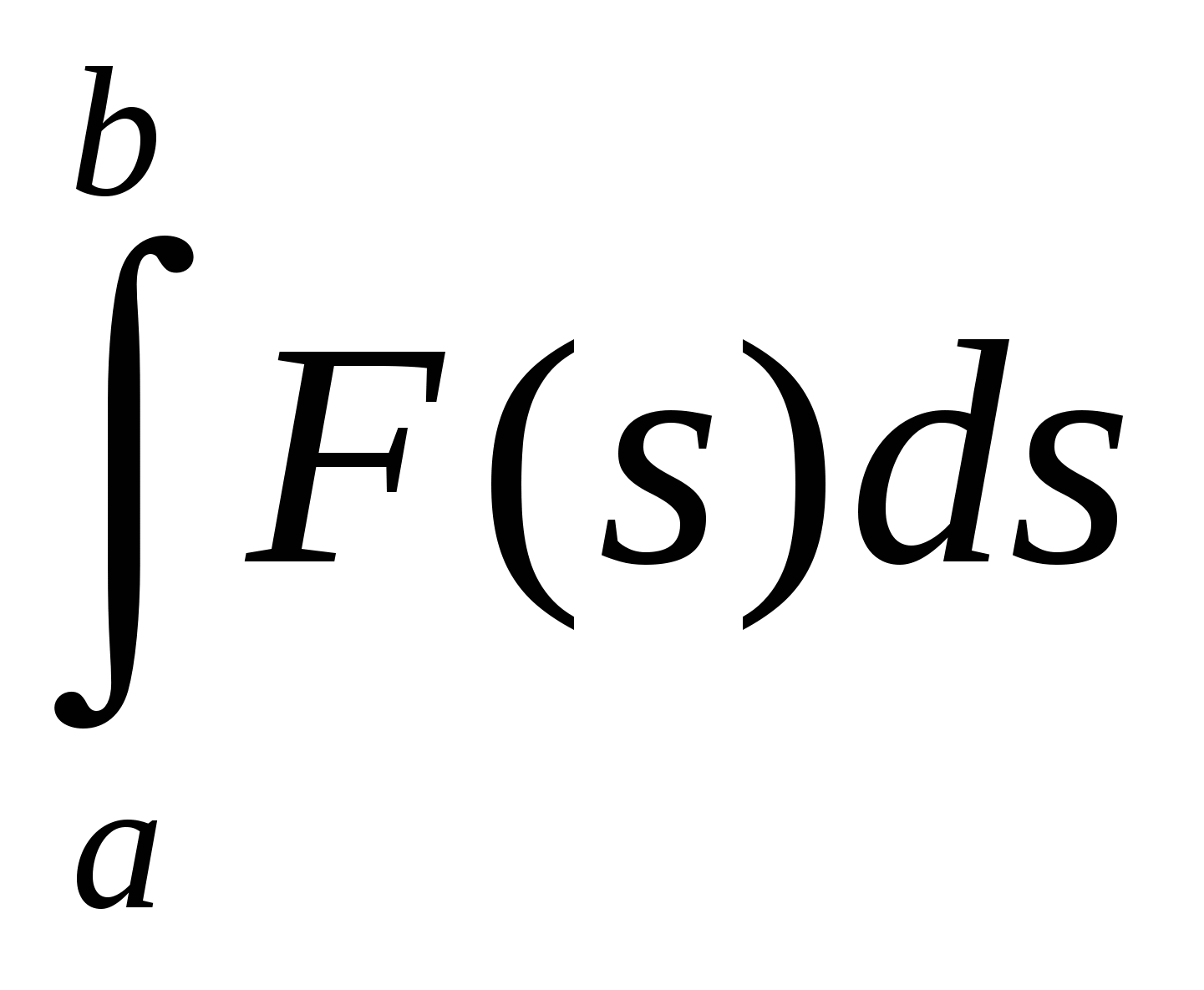

Используя полученную формулу перейдем к решению задачи.

По закону Гука сила F, растягивающая пружину на величину x, вычисляется по формуле F = kx, где - постоянный коэффициент пропорциональности. Из условия задачи следует, что 4 = 0,1k => k = 40 и сила F = 40x. Значит A =xdx = 20x|₀^0,05 = 20×0,0025 = 0,05Дж.

Учитель физики:

х₁=5см=0,05м А = kх₁²/2

F₂=4Н F₂=kх₂, k= F₂/ х₂, k=4/0,1=40

х₂=10см=01м А=400,05²/2= 0,05Дж

А=?

Учитель математики: Мы с вами решали задачи механики, используя методы физики и математики. А сейчас попробуйте применить знания, полученные на уроке, при выполнении самостоятельной работы.

4. Самостоятельная работа

Решаем задачи №4,5.

4. Тело движется со скоростью, возрастающей пропорционально времени. Найти уравнение движения, если в начальный момент путь тела S=0, а через t=5 с оно прошло путь S=15 м.
5. Вычислить работу, которую нужно затратить при растяжении пружины на 8 см, если сила в 3 Н растягивает пружину на 1 см.

Задача 5: 1 вариант - методами матанализа;

2 вариант - методами физики.

Задача 6: 1 вариант - методами физики;

2 вариант - методами матанализа.

Проверка (слайды ) и обсуждение решений.

5. Подведение итогов урока

Сегодня на уроке мы рассматривали решение физических задач с точки зрения математики, используя производную и первообразную и с точки зрения физики. Каждый вправе выбирать какой способ удобнее. Но каким бы образом вы не решали задачи необходимо уметь пользоваться математическим аппаратом. Ведь математика - инструмент физики. Не зря великий русский ученый Михаил Васильевич Ломоносов говорил: «Слеп физик без математики»

Надеемся, что рассмотренный материал поможет вам на экзаменах, как по математике, так и по физике.

6. Домашнее задание.

1. Скорость прямолинейно движущегося тела равна v(t) = 4t – t² .

Вычислить путь, пройденный телом от начала движения до остановки.

2. Вычислить работу, которую нужно затратить при сжатии пружины на

3 см, если сила в 2Н сжимает эту пружину на 1 см.

3. Высота h (в метрах), которой достигает за t секунд тело, брошенное

вертикально вверх со скоростью v₀ м/с, определяется уравнением

s = v₀t – 4,9t². Найти скорость и ускорение движения в момент t = 3 c,

если v₀ = 200м/с (сопротивление воздуха не учитывается).

4. Скорость точки задана уравнением v = 4соs(t) м/с. Найти уравнение

движения, если в момент t=π/6 точка находиться на расстоянии S=8 м

от начала отсчета пути.