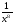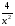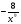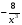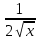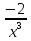Конспект урока «Применение производной при решении задач» по математике













 Тема: «Применение производной при решении задач.»
Тема: «Применение производной при решении задач.»
Цель:
-
Обобщить знания учащихся по теме «Применение производной функции.» .
-
Способствовать развитию навыков применения теоретических знаний в практической деятельности.
-
Способствовать воспитанию ответственности за качество и результат выполняемой работы на уроке.
Знать:
-
Где применяется производная,
-
алгоритмы нахождения экстремумов функции, наибольшего и наименьшего значения функции, нахождения уравнения касательной .
Уметь: применять алгоритмы при решении различных задач.
Тип урока: обобщение изучаемого материала и комплексного применения
знаний, умений и навыков при решении задач.
Оборудование: моноблок, оценочный лист и рефлексии;
карточки задания на каждом этапе урока.
Эпиграф: « Мудр – кто знает нужное, а не многое». Эсхил.
Ход урока.
I.Организационный момент.
-
Объявление девиза урока
-
Постановка учащимися целей и задач урока
-
Разделение учащихся на группы.
На протяжении всего урока вы будете заполнять оценочный лист и в конце по количеству набранных баллов вы сами оцените свою работу на уроке.
Оценочный лист
10 «А» класс.
| Устное повторение материала (самооценка) | Тест с выбором верного ответа (взаимооценка) | Эстафета (самооценка) | Групповая работа (взаимо оценка) | Установите соответствие (самооценка) | Тестированный контроль «Собери пару» (самооценка) | Дополнительное задание (взаимо оценка) | Оценка (ставит ученик) | Итоговая оценка | |
| | | | | | | | | | |
II.Повторение теоретического материала
«Вы уже накопили некоторый опыт нахождения производной. И сегодня мы посмотрим, чему же вы научились. Повторим теоретический материал».
Вам было дано задание, каждому подготовить вопросы на повторение. Вы разделились на группы. И теперь первая группа задаёт вопросы второй и третьей группам, вторая - первой и третьей, третья - первой и второй. Тот учащийся, который верно ответил на вопрос, ставит себе в оценочный лист 1 балл.
III.Разминка. Тест с выбором верного ответа
1 вариант
Найти производные функции:
-
у = 7 х5: а) 12х4 ; б) 35х6 ; в) 35х4.
-
у = 0,5х4 + х ; а) 2х3 - 1; б) 4,5х3 +1; в) 2х3 +1.
-
у =
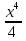 ; а) х3 ; б) 16х4 ; в)
; а) х3 ; б) 16х4 ; в) 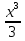 .
. -
у= х6 + 3
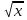 ; а) 6х5 +
; а) 6х5 +  ; б) 6х5 +
; б) 6х5 + 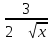 ; в) 6х5 + 6
; в) 6х5 + 6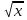 .
. -
у=
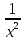 ; а) -
; а) -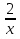 ; б)
; б)  ; в) -
; в) -  .
. -
у= 2х +5; а) -2 ; б) 2; в) 5.
2вариант
Найти производные функции:
1.у=3х9; а) 27х9 ; б) 27х8; в) 12х8.
2.у=3х5 – 2х; а) 8х4 – 2; б) 15х4 – 2х; в) 15х4 – 2.
3.у = 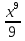 ; а) х8; б) 81х8; в)
; а) х8; б) 81х8; в) 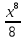 .
.
4.у = х4+ 2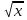 ; а) 4х3 +
; а) 4х3 + 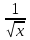 ; б) 4х3 +
; б) 4х3 +  ; в) 4х3+
; в) 4х3+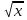
5.у = 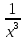 а)
а) 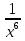 ; б)
; б)  ; в)
; в) 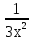 ;
;
6.у = -7х + 6 а) 7; б) -7; в) 6
3 вариант
Найти производные функции:
-
у = 5х4; а) 20х3; б) 20х5; в) 9х3;
2.у=5х3 – 4х; а) 8х4 – 4; б) 15х4 – 4х; в) 15х2 – 4.
3.у = 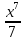 ; а) х6; б) 49х8; в)
; а) х6; б) 49х8; в) 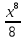 .
.
4.у = х6+ 6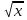 ; а) 6х6 +
; а) 6х6 + 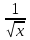 ; б) 6х5 +
; б) 6х5 +  ; в) 6х5+
; в) 6х5+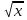
5.у = 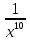 а)
а) 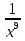 ; б)
; б) 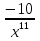 ; в)
; в) 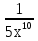 ;
;
6.у = -8х + 13 а) 8; б) -8; в) 5
Карточки с заданиями на столах. Каждое задание оценивается в 1 балл. (Взаимооценка)
IV.«Эстафета»
На доске каждому ученику даются задания на применение производной. Нужно быстро и правильно решить задание. За каждое верно выполненное задание ученик получает по одному баллу.
1) 7х+3 4)(5+х)*(5-х)
2)sin5 5)tgx-3х2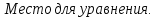
3) 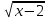 6)
6) 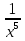
V.Работа в группах.
Предлагаются задания на нахождение экстремумов функции, наибольшего и наименьшего значения функции, нахождения уравнения касательной .Задания на столах. Представители групп вытягивают задания для групповой работы. В группах учащиеся обсуждают, решают задания. После того, как вы будете готовы, меняетесь в группах, и каждый из вас объясняет решение задания в своей новой группе.
-
Найти экстремумы функции f(x)=х4 – 8х2 + 6.
-
Запишите уравнение касательной функции у = -3х2 + 6х +1 в точке пересечения графика с осью ординат.
-
Найти наибольшее и наименьшее значение функции f(x) = 3х5 – 5х3 + 1 на отрезке [-2; 2].
VI. Установите соответствие
На доске задания для устного счета. Учащиеся выходят по одному к доске и стрелками устанавливают соответствие между верхней и нижней строчкой таблицы.
| 1. | 2. x+cosx | 3. sin2x | 4. cos2x | 5. | |
| | | | | | |
| Производная | А. 1-sinx | B. | C. -2sin2x | D. sin2x | E. |
VII.Индивидуальная работа: Составь пару.
Объяснение задания: в клетках таблицы записаны функции. Для каждой функции найдите её производную и запишите пару чисел: функция- производная. Правильный ответ: 1 балл. Цель: проверить знание таблицы производных.
| 6 | 11 | 16 | |
| х5 | х2 |
| а |
| 2 | 7 | 12 | 17 |
| Х |
| -3 | Cos x |
| 3 | 8 | 13 | 18 |
| 2x | Sin x | - Sin x |
|
| 4 | 9 | 14 | 19 |
| 1 | 5x4 |
| 0 |
| 5 | 10 | 15 | 20 |
| 2 | -3x-4 | ax | 12x-5 |
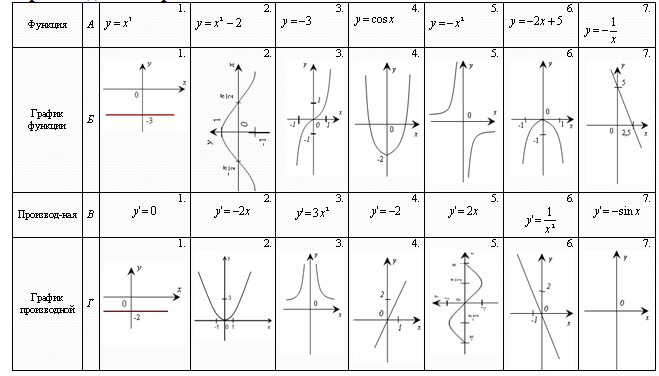
VIII. Дополнительные задания. Установи соответствие между функцией, записанной в строке А, ее изображением в строке Б, производной функции в строке В и графиком производной в строке Г.( оценивается – 1 балл). Цель: повторить графики функции 6 – 9 класс.
IX. Домашнее задание. Тест « проверь себя!» стр. 150 № 1 – 8.
X. Итог урока. Диаграмма ВЕННа
Производная
Рефлексия проводится по цветонастроению – учащиеся выбирают цвет который соответствует их настроению в конце урока, заполнение оценочного листа.
Цветонастроение: стикер Красного цвета – у вас все получалось, вы уходите с урока с хорошим настроением.
Зеленого цвета – у вас не все получалось, но настроение хорошее.
Желтого цвета – у вас не все получалось и от этого настроение ваше испорчено.
Ответы к тесту с выбором верного ответа.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Первый | в | в | а | б | в | б |
| Второй | б | в | а | а | б | б |
| Третий | а | в | а | б | б | б |
Ответы к тесту «Составь пару»
| 2-4 | 3-5 | 4-19 | 5-19 | 6-3 | 7-18 | 8-17 | |
| 10-20 | 11-14 | 12-19 | 15-16 | 16-19 | 17-13 | | |
Дополнительные задания
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Б | 3 | 4 | 1 | 2 | 6 | 7 | 5 |
| В | 3 | 5 | 1 | 7 | 2 | 4 | 6 |
| Г | 2 | 4 | 7 | 5 | 6 | 1 | 3 |
Ответы к тесту с выбором верного ответа.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Первый | в | в | а | б | в | б |
| Второй | б | в | а | а | б | б |
| Третий | а | в | а | б | б | б |
Ответы к тесту «Составь пару»
| 2-4 | 3-5 | 4-19 | 5-19 | 6-3 | 7-18 | 8-17 | |
| 10-20 | 11-14 | 12-19 | 15-16 | 16-19 | 17-13 | | |
Дополнительные задания
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Б | 3 | 4 | 1 | 2 | 6 | 7 | 5 |
| В | 3 | 5 | 1 | 7 | 2 | 4 | 6 |
| Г | 2 | 4 | 7 | 5 | 6 | 1 | 3 |
1 вариант
Найти производные функции:
1.у = 7 х5: а) 12х4 ; б) 35х6 ; в) 35х4.
2.у = 0,5х4 + х ; а) 2х3 - 1; б) 4,5х3 +1; в) 2х3 +1.
3.у = 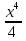 ; а) х3 ; б) 16х4 ; в)
; а) х3 ; б) 16х4 ; в) 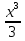 .
.
4. у= х6 + 3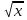 ; а) 6х5 +
; а) 6х5 +  ; б) 6х5 +
; б) 6х5 + 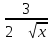 ; в) 6х5 + 6
; в) 6х5 + 6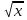 .
.
5.у= 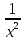 ; а) -
; а) -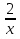 ; б)
; б)  ; в) -
; в) -  .
.
6. у= 2х +5; а) -2 ; б) 2; в) 5.
2вариант
Найти производные функции:
1.у=3х9; а) 27х9 ; б) 27х8; в) 12х8.
2.у=3х5 – 2х; а) 8х4 – 2; б) 15х4 – 2х; в) 15х4 – 2.
3.у = 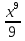 ; а) х8; б) 81х8; в)
; а) х8; б) 81х8; в) 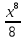 .
.
4.у = х4+ 2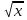 ; а) 4х3 +
; а) 4х3 + 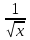 ; б) 4х3 +
; б) 4х3 +  ; в) 4х3+
; в) 4х3+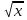
5.у = 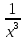 а)
а) 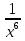 ; б)
; б)  ; в)
; в) 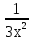 ;
;
6.у = -7х + 6 а) 7; б) -7; в) 6
3 вариант
Найти производные функции:
1.у = 5х4; а) 20х3; б) 20х5; в) 9х3;
2.у=5х3 – 4х; а) 8х4 – 4; б) 15х4 – 4х; в) 15х2 – 4.
3.у = 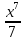 ; а) х6; б) 49х8; в)
; а) х6; б) 49х8; в) 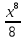 .
.
4.у = х6+ 6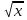 ; а) 6х6 +
; а) 6х6 + 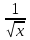 ; б) 6х5 +
; б) 6х5 +  ; в) 6х5+
; в) 6х5+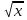
5.у = 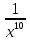 а)
а) 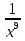 ; б)
; б) 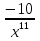 ; в)
; в) 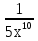 ;
;
6.у = -8х + 13 а) 8; б) -8; в) 5
Здесь представлен конспект к уроку на тему «Применение производной при решении задач», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.