Школьная олимпиада по математике

Часть А

Задачи, оцениваемые в 3 балла

1. Яблоко и апельсин вместе весят столько же, сколько груша и персик.

Яблоко вместе с грушей весят меньше, чем апельсин с персиком, а гру-

ша вместе с апельсином весят меньше, чем яблоко с персиком. Какой

из фруктов самый тяжёлый?

Ответ __________________________________

2. В классе сидят мальчики и девочки. Если в класс войдут ещё 10 мальчиков,

то всего мальчиков станет вдвое больше, чем девочек. Сколько девочек

должны выйти из класса, чтобы среди оставшихся ребят оказалось вдвое

больше мальчиков, чем девочек?

Ответ __________________________________

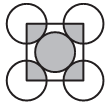
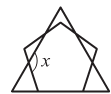
3. На рисунке изображены квадрат и пять одинаковых

кругов. Вершины квадрата расположены в центрах

внешних кругов. Тогда отношение площади закра-

шенной части кругов к площади их незакрашенной

части равно:

Ответ __________________________________

4. Катя и четыре её подружки разделили между собой несколько конфет.

В результате оказалось, что у всех девочек разное число конфет, а общее

число конфет у Кати и двух девочек больше, чем общее число конфет у

остальных двух. Какое самое маленькое число конфет может быть у Кати?

Ответ __________________________________

5. Сколько двузначных чисел обладают таким свойством: если переставить

местами их цифры, то они увеличиваются не менее, чем в три раза?

Ответ __________________________________

6. Если разделить 50⁵⁰ на 25²⁵, то получится:

Ответ __________________________________

7. На рисунке изображены равносторонний треугольник

и правильный пятиугольник. Найдите угол х.

Ответ __________________________________

8. Вокруг прямоугольного сквера проложена дорожка,

которая на всём своём протяжении имеет одинако-

вую ширину. Наружная граница дорожки на 8 метров

длиннее внутренней. Чему равна ширина дорожки?

Ответ __________________________________

Часть В

Задачи, оцениваемые в 4 балла

9. Числа а и b таковы, что 4 ≤ а ≤ 6, 1 ≤ b ≤ 2. Какое из следующих чисел

обязательно меньше 9?

а) 3а – 2b; б) а + 2b; в) 3а – b; г) 8b – 2а; д) 13b – а.

10. На стороне ВС равнобедренного треугольника АВС с основанием АС

нашлась такая точка М, что МСА – МАВ = В. Что можно утверждать

об этом треугольнике?

а) он равносторонний; в) боковая сторона больше основания;

б) один из его углов прямой; г) угол при вершине В – тупой.

11. Диагональ делит четырёхугольник с периметром 31см на два треуголь-

ника с периметрами 21см и 30см. Какова длина этой диагонали?

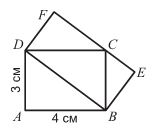
Ответ __________________________________

12. Два прямоугольника ABCD и DBEF расположены

так, как показано на чертеже. Какова площадь

прямоугольника DBEF?

Ответ __________________________________

№ задания

1	2	3			4		5		6			7		8		9			10		11		12		Всего баллов
Количество баллов