КОМПЛЕКТ ЭКЗАМЕНАЦИОННЫХ ТЕСТОВ ПО МАТЕМАТИКЕ (для студентов 1 курса дневного отделения)
Государственное автономное профессиональное образовательное учреждение Саратовской области
«Энгельсский колледж профессиональных технологий»
| Утверждаю Зам. директора по УМР Карюкина О.А. ____________________________ «____»________________20__г. |
КОМПЛЕКТ ЭКЗАМЕНАЦИОННЫХ ТЕСТОВ
по дисциплине
«МАТЕМАТИКА»
(цикл общеобразовательный дисциплин)
для студентов 1 курса дневного отделения
г. Энгельс
2014 год
| Утверждаю Зам. директора по УМР Карюкина О.А. ____________________________ «____»________________20__г. |
1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Данный экзаменационный материал дисциплины «Математика» соответствует государственным требованиям к минимуму содержания и уровню подготовки выпускников
В экзаменационной работе нашли отражения концептуальные положения Федерального государственного образовательного стандарта 3 поколения. Экзаменационная работа разработана с учетом положения, что результатом освоения основной образовательной программы должна стать математическая компетентность выпускников, т.е. они должны не только овладеть специфическими для математики знаниями и видами деятельности, но и научится преобразованию знания и его применения в учебных и внеучебных ситуациях, сформировать качества присущие математическому мышлению, овладеть математической терминологией, ключевыми понятиями, методами и приемами.
Структура работы отвечает цели построения системы дифференцированного обучения.
Работа состоит из двух частей. При выполнении задний первой части (1 – 11) студенты должны продемонстрировать базовую математическую компетентность. В этой части проверяется владение основными алгоритмами, знаниями и понимание ключевых элементов содержания, умение пользоваться математической записью, решать математические задачи, сводящиеся к прямому применению алгоритма. При выполнении заданий студент должен выбрать правильный ответ из предложенных и записать их в бланк ответов № 1
Задания второй части (12 – 16) направлены на проверку таких качеств математической подготовки , как:
-
уверенное владение математическим аппаратом;
-
умение решать задачу , включающую в себя знания из разных тем курса;
-
умение математически грамотно и ясно записать решение, приводя при этом необходимые пояснения и обоснования.
При выполнении задании 12 – 16 студент должен воспользоваться бланком ответа № 2 для записи развернутого решения задачи.
По окончанию изучения курса дисциплины «Математика» студент должен обладать общими компетенциями (ОК) 1 – 10 и профессиональными компетенциями (ПК) 1.1 – 3.5.
На основании изучения пройденного материала по дисциплине «Математика» и освоения экзаменационных вопрос студент должен успешно сдать экзамен.
Паспорт теста
Дисциплина «Математика»
Общее количество часов: 290
Количество вариантов: 10
Количество вопросов в тесте: 16
Время проведения: 3 академических часа
Для оценивания результатов выполнения работ применяется такой количественный показатель как общий бал.
| Максимальное количество баллов | |||
| Часть 1 | Часть 2 | Часть 1 | Часть 2 |
| Задания 1 – 11 | Задание 12 – 16 | 55 | 45 |
| 5 | 9 |
Шкала пересчета общего балла за выполнение экзаменационной работы в отметку по пятибалльной шкале
| 0 – 49 | 50 – 69 | 70 – 89 | 90 – 100 | |
| Отметка по пятибалльной шкале | «2» | «3» | «4» | «5» |
2 .ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ
Математика в науке, технике, экономике, информационных технологиях и практической деятельности.
АЛГЕБРА
-
Целые и рациональные числа. Действительные числа.
-
Приближенные вычисления. Приближенное значение величины и погрешности приближений.
-
Корни и степени. Корни натуральной степени из числа и их свойства.
-
Степени с рациональными показателями, их свойства.
-
Степени с действительными показателями. Свойства степени с действительным показателем.
-
Логарифм. Логарифм числа. Основное логарифмическое тождество.
-
Десятичные и натуральные логарифмы. Правила действий с логарифмами. Переход к новому основанию.
-
Радианная мера угла. Вращательное движение.
-
Синус, косинус, тангенс и котангенс числа.
-
Основные тригонометрические тождества, формулы приведения.
-
Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Формулы половинного угла.
-
Простейшие тригонометрические уравнения. Решение тригонометрических уравнений.
-
Функции. Область определения и множество значений, график функции.
-
Свойства функции: монотонность, четность, нечетность, ограниченность, периодичность. Промежутки возрастания и убывания.
-
Примеры функциональных зависимостей в реальных процессах и явлениях.
-
Обратные функции. Область определения и область значений обратной функции. График обратной функции.
-
Определение степенной функции, ее свойства и график.
-
Определение показательной функции, ее свойства и график.
-
Определение логарифмической функции, ее свойства и график.
-
Определение тригонометрических функций, их свойства и графики.
-
Обратные тригонометрические функции.
-
Преобразования графиков. Параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой у = х, растяжение и сжатие вдоль осей координат.
НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
-
Последовательности. Способы задания и свойства числовых последовательностей. Понятие о пределе последовательности.
-
Существование предела монотонной ограниченной последовательности. Суммирование последовательностей.
-
Бесконечно убывающая геометрическая прогрессия и ее сумма.
-
Понятие о непрерывности функции.
-
Производная. Понятие о производной функции, её геометрический и физический смысл.
-
Уравнение касательной к графику функции.
-
Производные суммы, разности, произведения, частного.
-
Применение производной к исследованию функций и построению графиков.
-
Примеры использования производной для нахождения наилучшего решения в прикладных задачах.
-
Первообразная и интеграл. Основные формулы интегрирования.
-
Определенный и неопределенный интеграл. Принципиальное отличие.
-
Применение определенного интеграла для нахождения площади криволинейной трапеции. Формула Ньютона—Лейбница.
-
Примеры применения интеграла в физике и геометрии.
УРАВНЕНИЯ И НЕРАВЕНСТВА
-
Равносильность уравнений, неравенств, систем.
-
Рациональные, иррациональные, показательные и тригонометрические уравнения и системы. Основные приемы их решения (разложение на множители, введение новых неизвестных, подстановка, графический метод).
-
Рациональные, иррациональные, показательные и тригонометрические неравенства. Основные приемы их решения.
-
Использование свойств и графиков функций при решении уравнений и неравенств.
-
Методы решения систем линейных алгебраических уравнений: метод Крамера, метод Гаусса.
-
Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
-
Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.
КОМБИНАТОРИКА, СТАТИСТИКА И ТЕОРИЯ ВЕРОЯТНОСТЕЙ
-
Основные понятия комбинаторики.
-
Задачи на подсчет числа размещений, перестановок, сочетаний. Решение задач на перебор вариантов.
-
Событие, вероятность события, сложение и умножение вероятностей.
-
Понятие о независимости событий.
-
Дискретная случайная величина, закон ее распределения. Числовые характеристики дискретной случайной величины.
-
Представление данных (таблицы, диаграммы, графики), генеральная совокупность, выборка, среднее арифметическое, медиана.
-
Понятие о задачах математической статистики.
ГЕОМЕТРИЯ
-
Взаимное расположение двух прямых в пространстве.
-
Параллельность прямой и плоскости. Параллельность плоскостей.
-
Перпендикулярность прямой и плоскости. Перпендикуляр и наклонная. Угол между прямой и плоскостью.
-
Двугранный угол. Угол между плоскостями. Перпендикулярность двух плоскостей.
-
Геометрические преобразования пространства: параллельный перенос, симметрия относительно плоскости.
-
Вершины, ребра, грани многогранника. Развертка. Выпуклые многогранники.
-
Призма. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб.
-
Пирамида. Правильная пирамида. Усеченная пирамида. Тетраэдр.
-
Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр).
-
Цилиндр. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения, параллельные основанию.
-
Конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения, параллельные основанию.
-
Объем и его измерение.
-
Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра.
-
Формулы объема пирамиды и конуса.
-
Формулы площади поверхностей цилиндра и конуса.
-
Формулы объема шара и площади сферы.
-
Прямоугольная (декартова) система координат в пространстве.
-
Формула расстояния между двумя точками. Уравнения сферы, плоскости и прямой.
-
Векторы. Модуль вектора. Равенство векторов. Сложение векторов.
-
Умножение вектора на число. Разложение вектора по направлениям. Угол между двумя векторами.
-
Проекция вектора на ось. Координаты вектора. Скалярное произведение векторов.
-
Использование координат и векторов при решении математических и прикладных задач.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Найдите значение выражения
1. ![]()
2. ![]()
3. ![]() .
.
Решите задачу:
-
Ковер прямоугольной формы со сторонами 2 м и 6 м покрывает
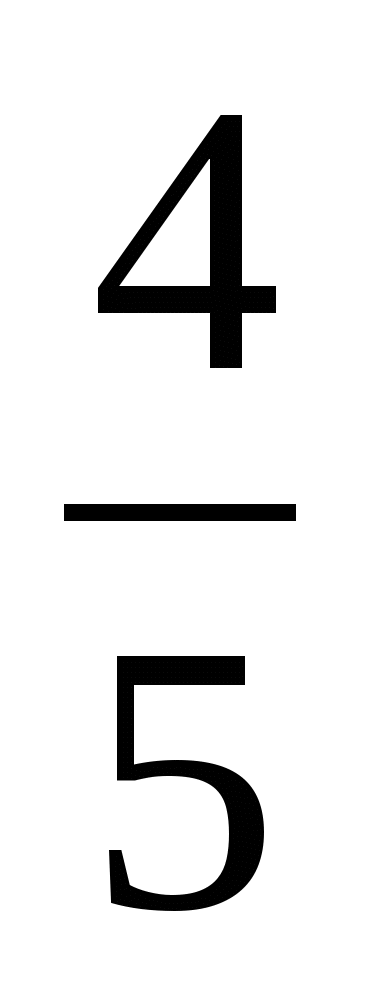 площади пола комнаты. Какова площадь комнаты?
площади пола комнаты. Какова площадь комнаты? -
В первый день велосипедист проехал 52% маршрута, во второй - в два раза меньше, а в третий - оставшиеся 44 км. Какова протяженность маршрута велосипедиста?
-
Расстояния от села А до сел Б и В пропорциональны числам 3 и 5. Чему равно каждое из этих расстояний, если село Б находится на 8 км ближе к селу А, чем В?
-
На пост председателя комитета претендовали кандидаты А и В. в голосовании приняли участие 198 человек, причем голоса распределились между кандидатами в отношении 8:3. На сколько больше голосов получил победитель?
Найдите значение выражения
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
5. ![]() ;
;
6. 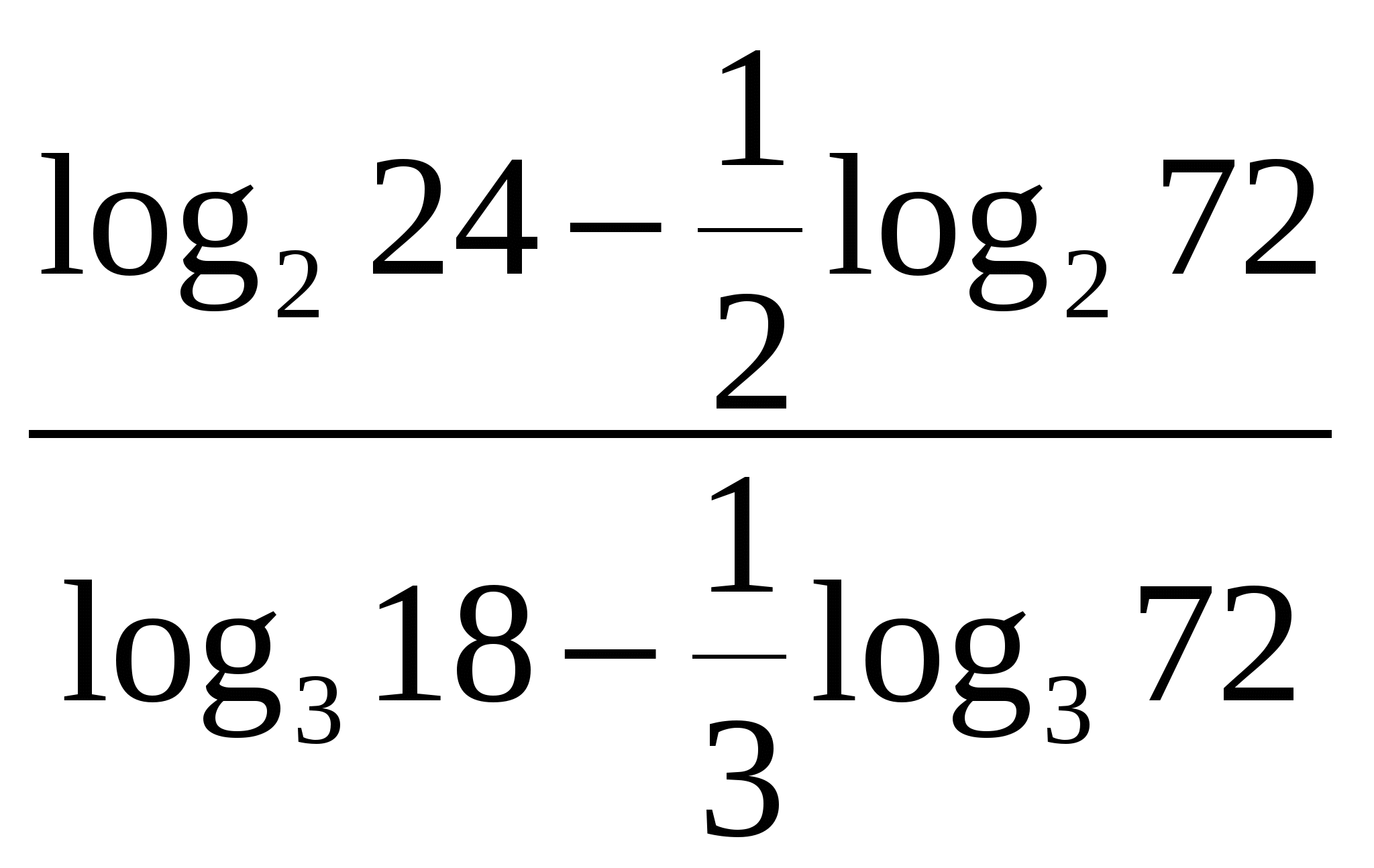 ;
;
7. ![]() ;
;
8. ![]() ;
;
9. ![]() ;
;
10. ![]() ;
;
11. ![]() ;
;
12. ![]() .
.
Решите задачи
-
Из точки А к данной плоскости проведены перпендикуляр и наклонная, пересекающие плоскость соответственно в точках В и С. Найдите отрезок АС, если АВ=10см,
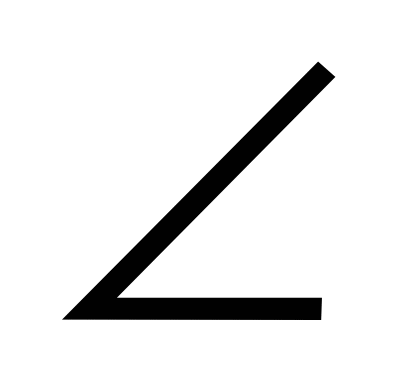 ВАС = 30°.
ВАС = 30°.
-
Отрезки двух наклонных, проведенных из одной точки к плоскости, равны 16 см и 22 см. Проекция одного из этих отрезков равна 18 см. Найдите проекцию другого отрезка.
-
Из точки А к данной плоскости проведены перпендикуляр и наклонная, пересекающие плоскость соответственно в точках В и С. Найдите отрезок АВ, если АС=
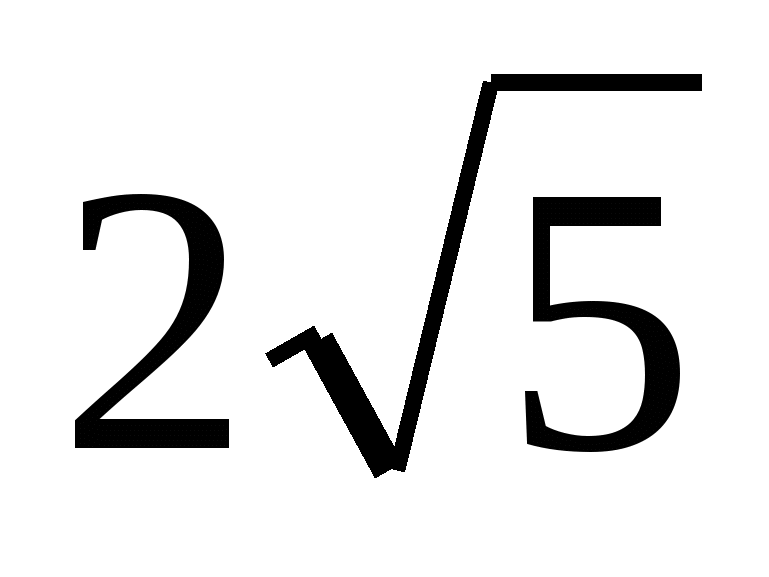 см, ВС = 2АВ.
см, ВС = 2АВ.
-
Дан прямоугольный треугольник ABC, катеты которого АС и ВС равны соответственно 20 и 15 см. Через вершину А проведена плоскость
 , параллельная прямой ВС. Проекция одного из катетов на эту плоскость равна 12 см. Найдите проекцию гипотенузы.
, параллельная прямой ВС. Проекция одного из катетов на эту плоскость равна 12 см. Найдите проекцию гипотенузы.
-
Из точки А к данной плоскости проведены перпендикуляр и наклонная, пересекающие плоскость соответственно в точках В и С. Найдите отрезок АС, если СВ = 8 см,
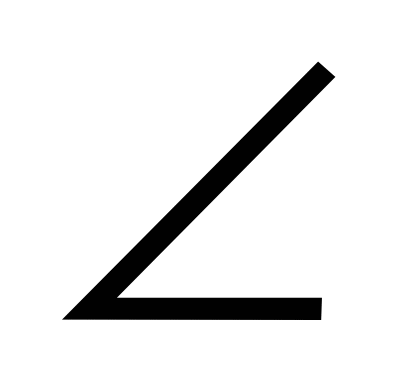 ВАС = 45°.
ВАС = 45°.
-
Отрезки двух наклонных, проведенных из одной точки к плоскости, равны 10 см и 20 см. Проекция одного из этих отрезков равна 7 см. Найдите проекцию другого отрезка.
-
Из точки А к данной плоскости проведены перпендикуляр и наклонная, пересекающие плоскость соответственно в точках В и С. Найдите отрезок АВ, если АС=
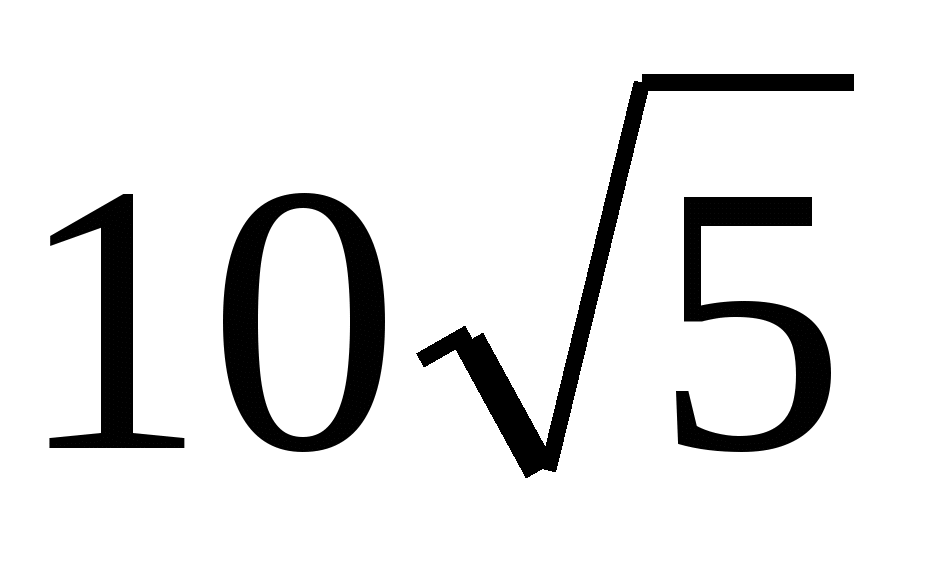 см, АВ = 3ВС.
см, АВ = 3ВС.
-
Дан прямоугольный треугольник ABC, катеты которого АС и ВС равны соответственно 20 и 15 см. Через вершину А проведена плоскость
 , параллельная прямой ВС. Проекция одного из катетов на эту плоскость равна 14 см. Найдите проекцию гипотенузы.
, параллельная прямой ВС. Проекция одного из катетов на эту плоскость равна 14 см. Найдите проекцию гипотенузы.
-
В прямоугольной декартовой системе координат постройте многоугольник вершинами которого являются следующие точки: А ( 4; 3), В (4; 1), С ( 3; – 2), D (1; – 1),
Е (– 2; – 2), F (– 4; 3), К (1; 5).
-
В прямоугольной системе координат вектор задается двумя точками А (– 4; 2) и
В (3; – 4). Найдите координаты вектора, длину вектора, середину данного вектора. Постройте этот вектор в прямоугольной системе координат.
-
Прямая проходит через две точки А (2; 5) и В (– 3; 0). Напишите уравнение прямой. Найдите угловой коэффициент. Постройте прямую в прямоугольной декартовой системе координат.
-
В прямоугольной системе координат вектор задается двумя точками А (1; 3; 7) и
В (3; 4; 10). Найдите координаты вектора и длину вектора. Постройте этот вектор в прямоугольной декартовой системе координат в пространстве.
-
Найдите угол между векторами
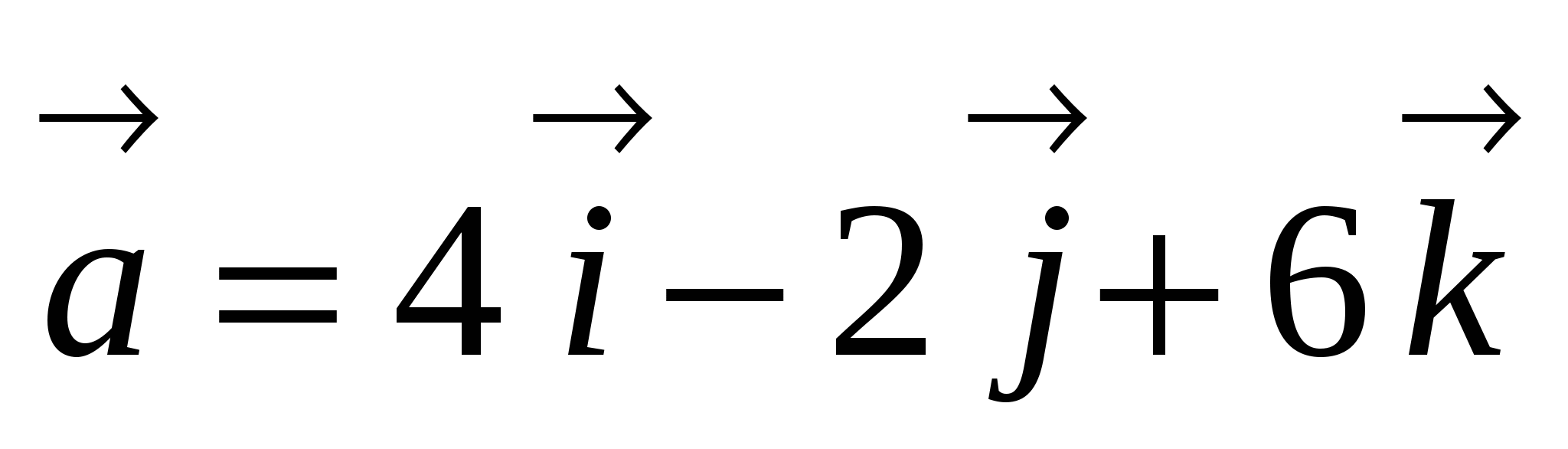 и
и 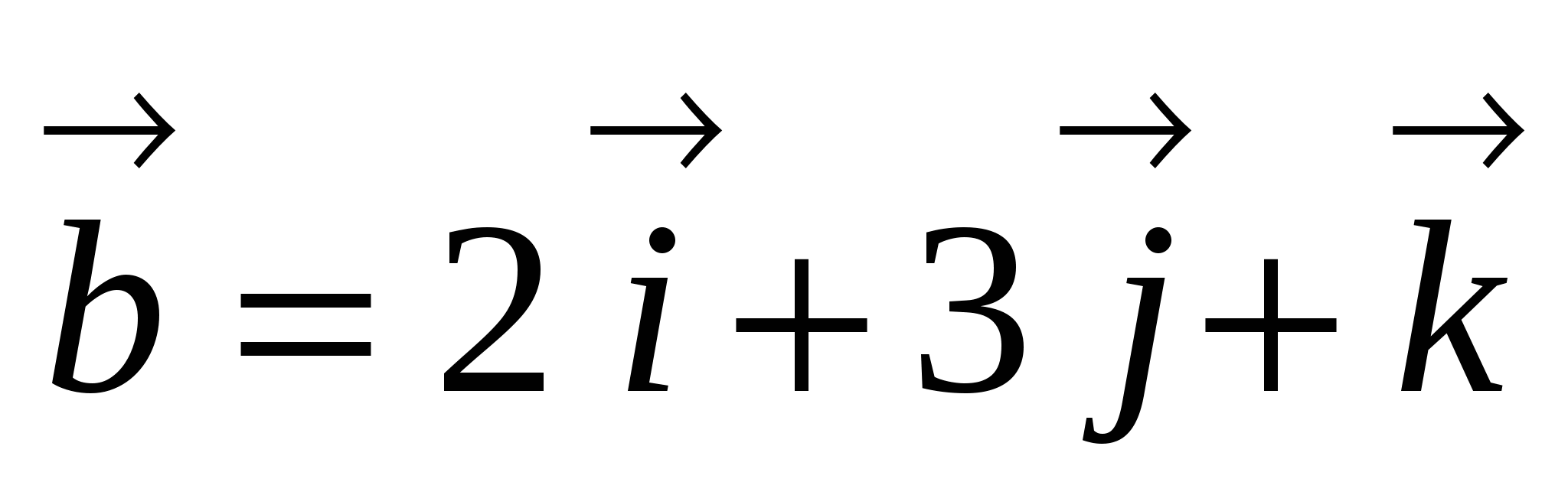 .
.
-
В прямоугольной декартовой системе координат постройте многоугольник вершинами которого являются следующие точки: А (– 5; 6), В (– 2; 6), С (1; 2), D (5; 2),
Е (1; – 2), F (– 6; 0).
-
В прямоугольной системе координат вектор задается двумя точками А (5; – 4) и
В (– 4; – 2). Найдите координаты вектора, длину вектора, середину данного вектора. Постройте этот вектор в прямоугольной системе координат.
-
Прямая проходит через две точки А (4; 8) и В (– 2; 4). Напишите уравнение прямой. Найдите угловой коэффициент. Постройте прямую в прямоугольной декартовой системе координат.
-
В прямоугольной системе координат вектор задается двумя точками А (2; 2; 4) и
В (4; 4; 7). Найдите координаты вектора и длину вектора. Постройте этот вектор в прямоугольной декартовой системе координат в пространстве.
-
Найдите угол между векторами
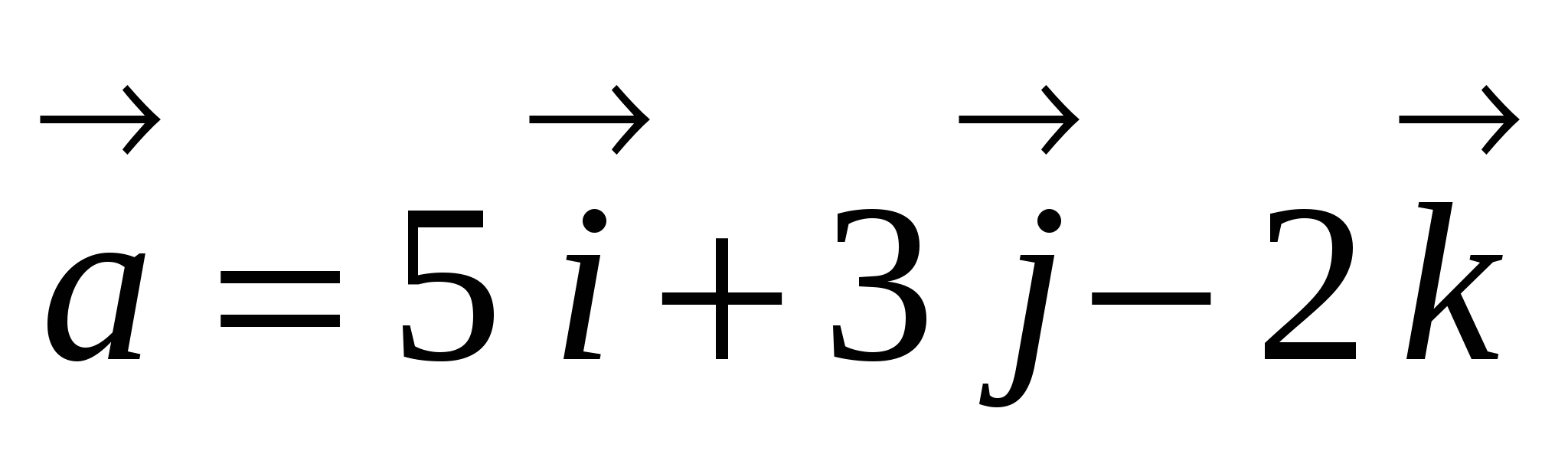 и
и 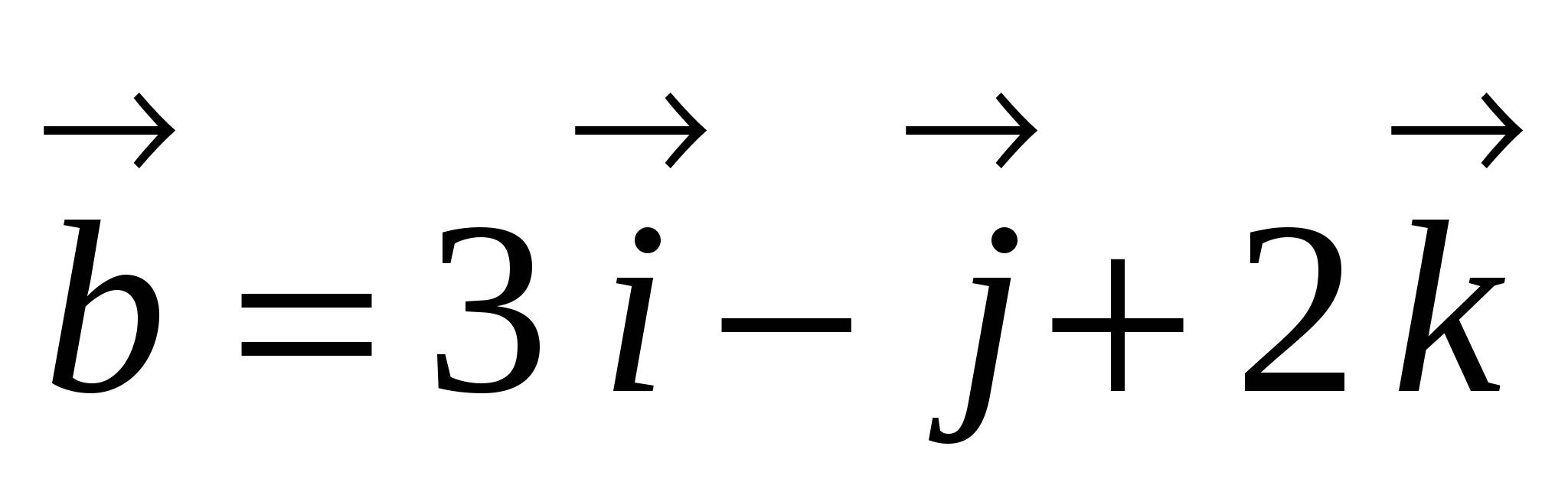 .
.
Найдите область определения функции
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
5. ![]() ;
;
6. ![]() .
.
Постройте график функции:
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() .
.
Найти значение производной функции в точке:
1. ![]() в точке
в точке ![]()
![]()
2. ![]() в точке
в точке ![]()
![]()
3. ![]() в точке
в точке ![]()
![]()
4. ![]() в точке
в точке ![]()
![]()
5. ![]() в точке
в точке ![]()
![]()
6. ![]() в точке
в точке ![]()
![]()
Исследовать функцию на экстремумы
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() .
.
Найти первообразную функции f(x) в точке М
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
5. ![]() ;
;
6. ![]() .
.
Решите задачи:
-
В мешке находятся шары различные только по цвету: 8 – белых, 9 – зеленых, 8 – красных. Вытаскиваем наугад один шар.
-
Какова вероятность того, что извлеченный из мешка шар окажется белым?
-
Какова вероятность того, что наугад извлеченный шар из задачи окажется либо красным, либо зеленым?
-
-
В мешке находятся шары различные только по цвету: 9 – белых, 12 – зеленых, 8 – красных. Вытаскиваем наугад один шар.
а) Какова вероятность того, что извлеченный из мешка шар окажется белым?
б) Какова вероятность того, что наугад извлеченный шар из задачи окажется либо красным, либо зеленым?
-
В мешке находятся шары различные только по цвету: 13 – белых, 8 – зеленых, 5 – красных. Вытаскиваем наугад один шар.
а) Какова вероятность того, что извлеченный из мешка шар окажется белым?
б) Какова вероятность того, что наугад извлеченный шар из задачи окажется либо красным, либо зеленым?
-
Найдите число сочетаний 12 элементов по 7.
-
Найдите число сочетаний 11 элементов по 5.
-
Найдите число сочетаний 13 элементов по 8.
-
Найдите число размещений 8 элементов по 4.
-
Найдите число размещений 12 элементов по 8.
-
Найдите число размещений 10 элементов по 4.
-
Найдите число перестановок пяти элементов.
-
Найдите число перестановок четырех элементов.
Решите систему уравнений:
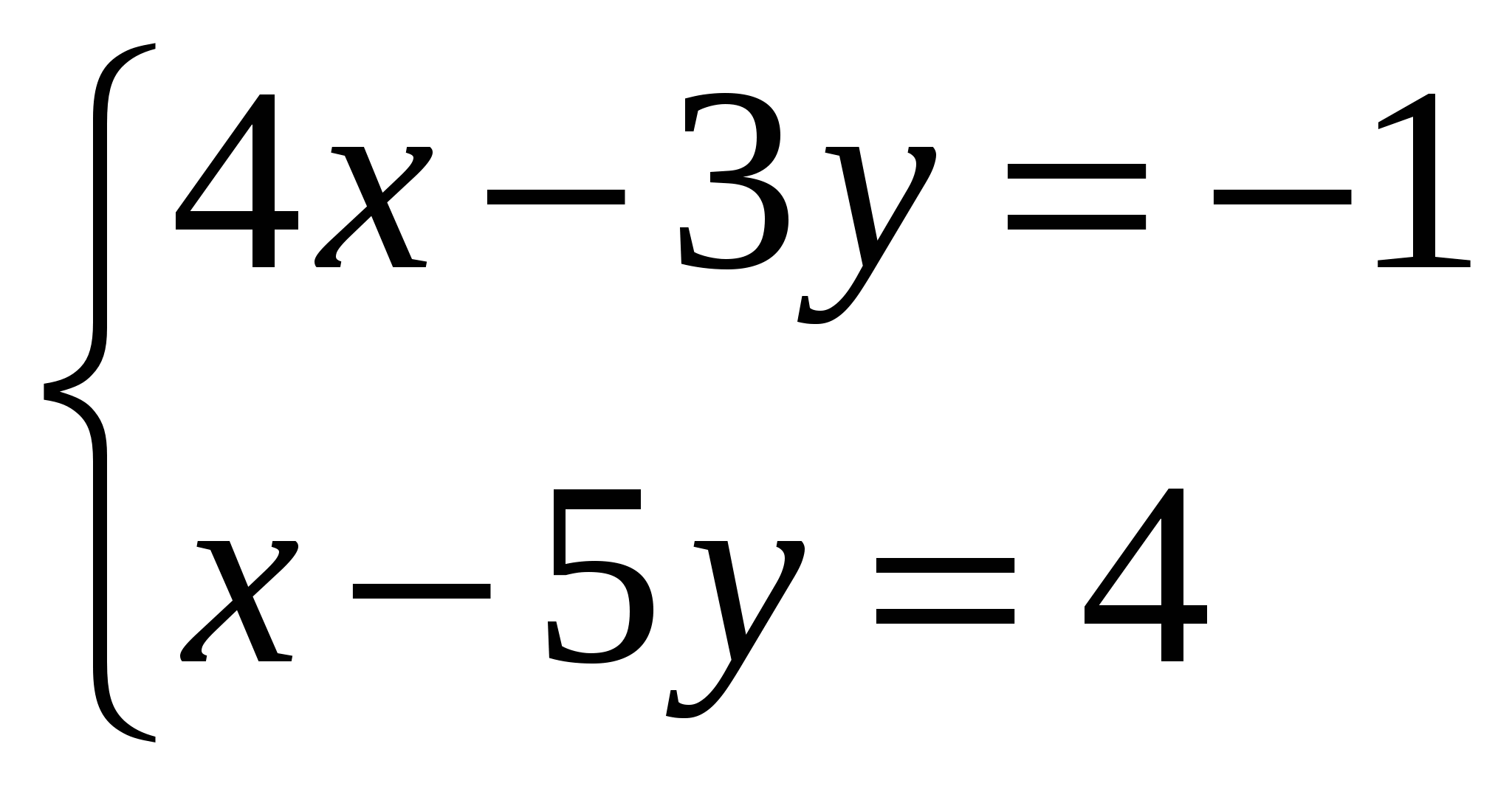
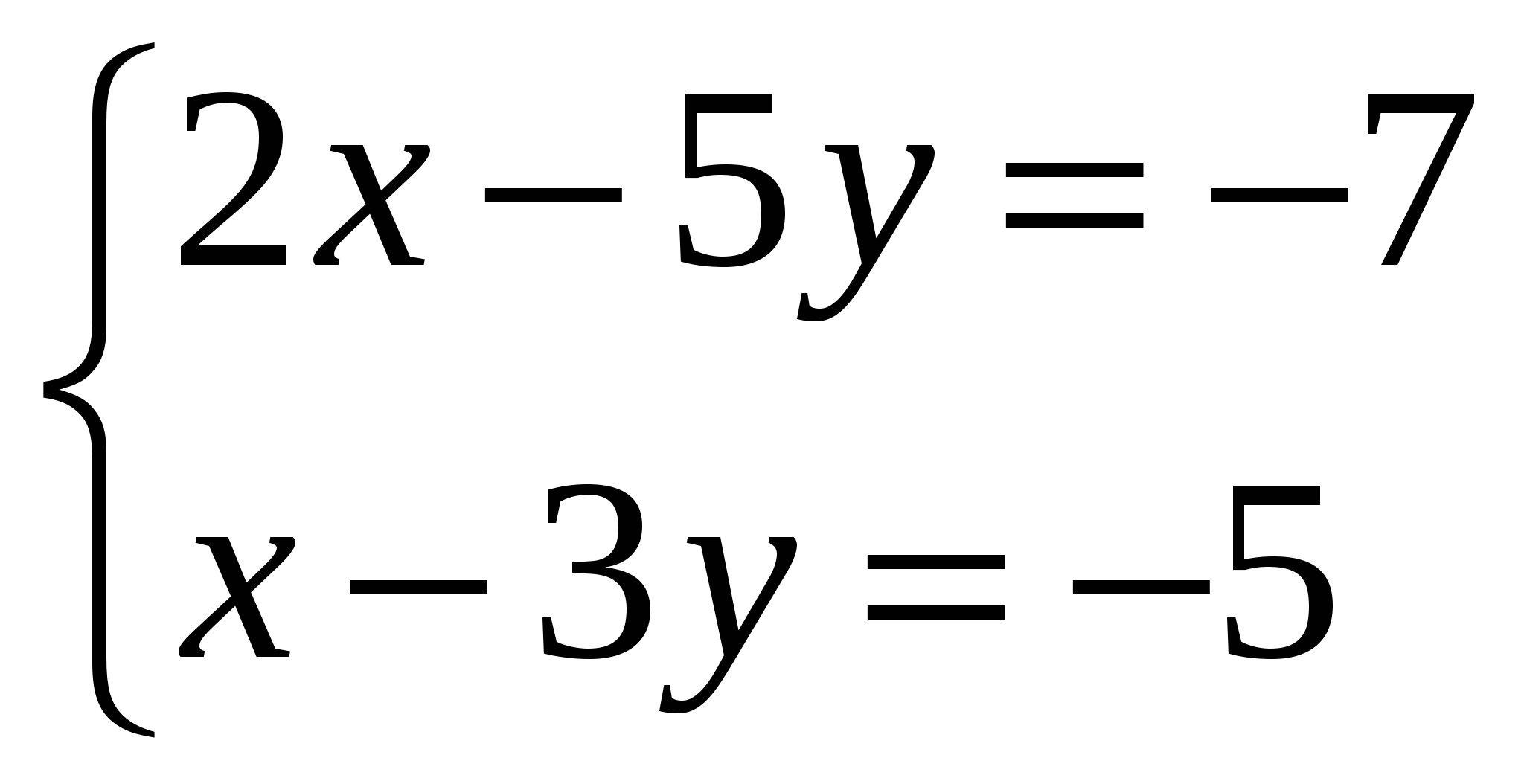
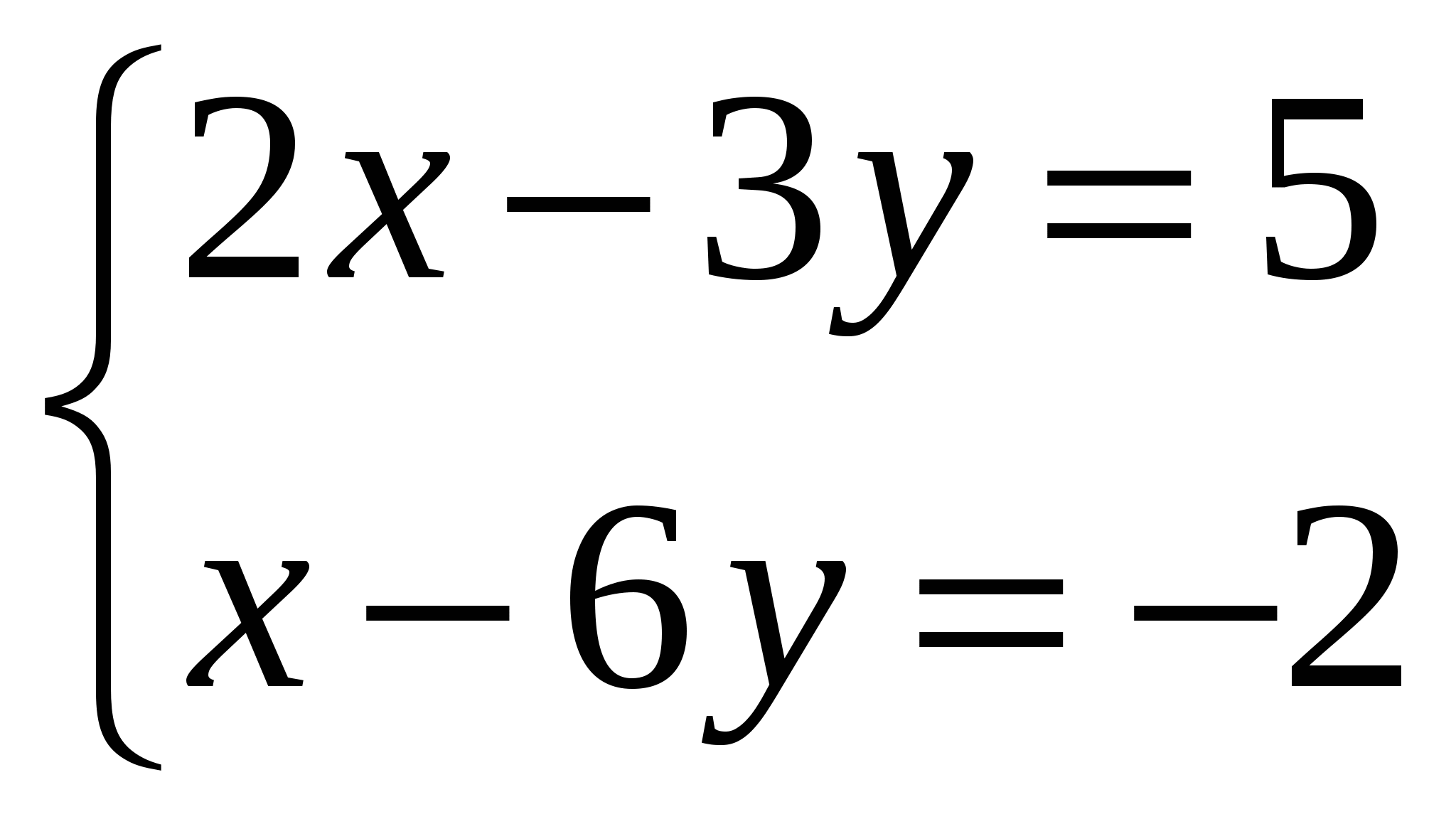
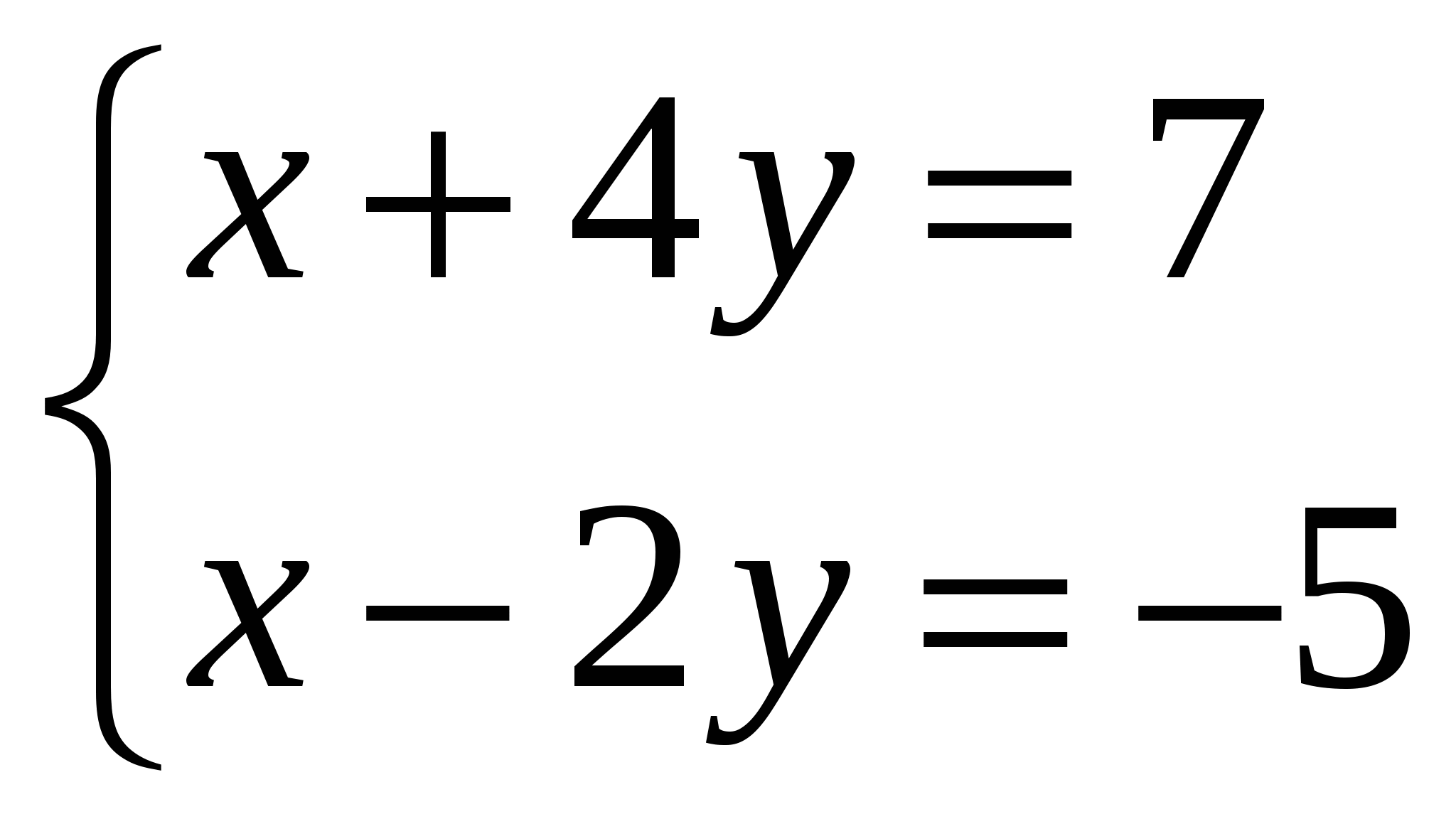
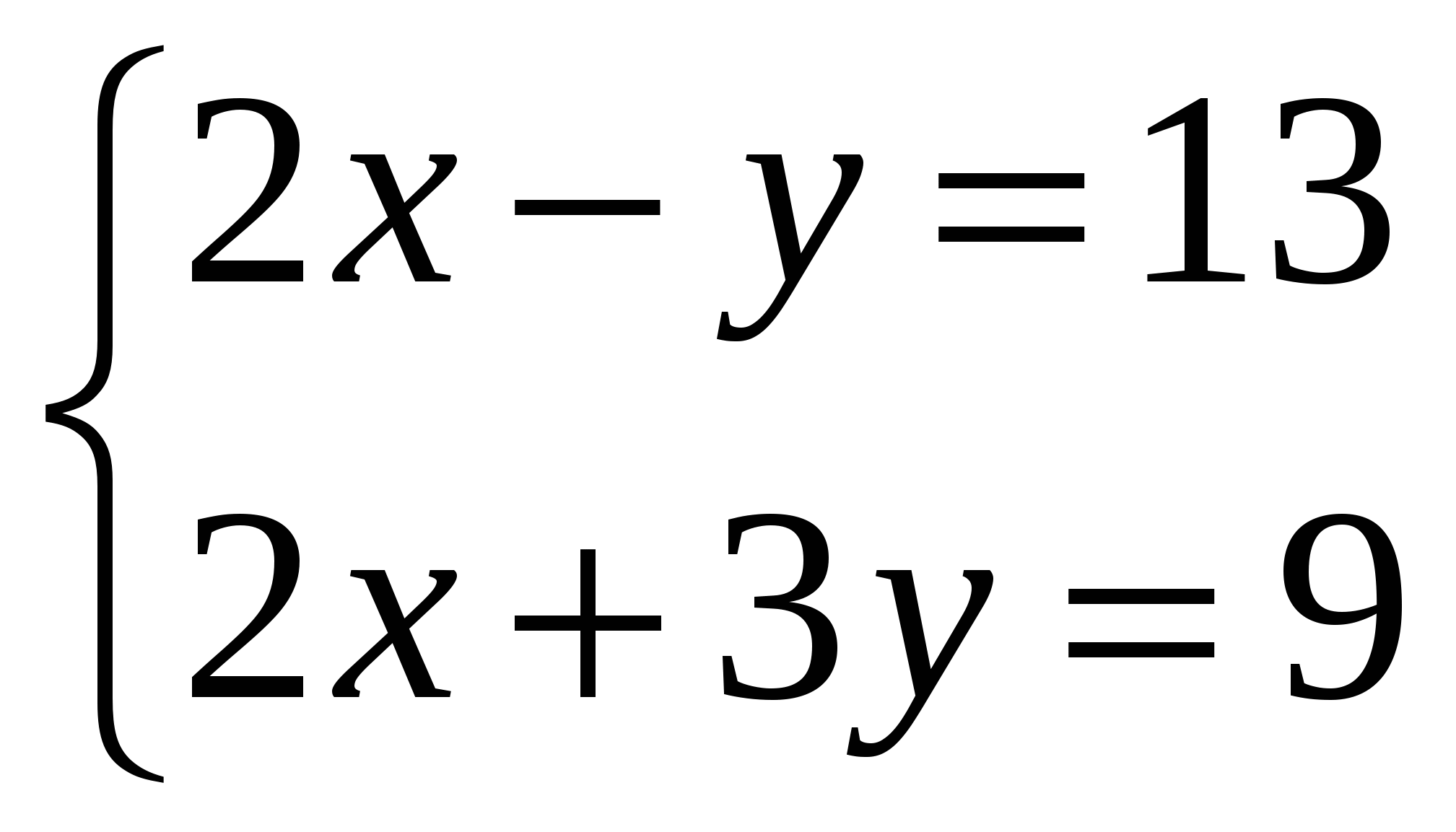
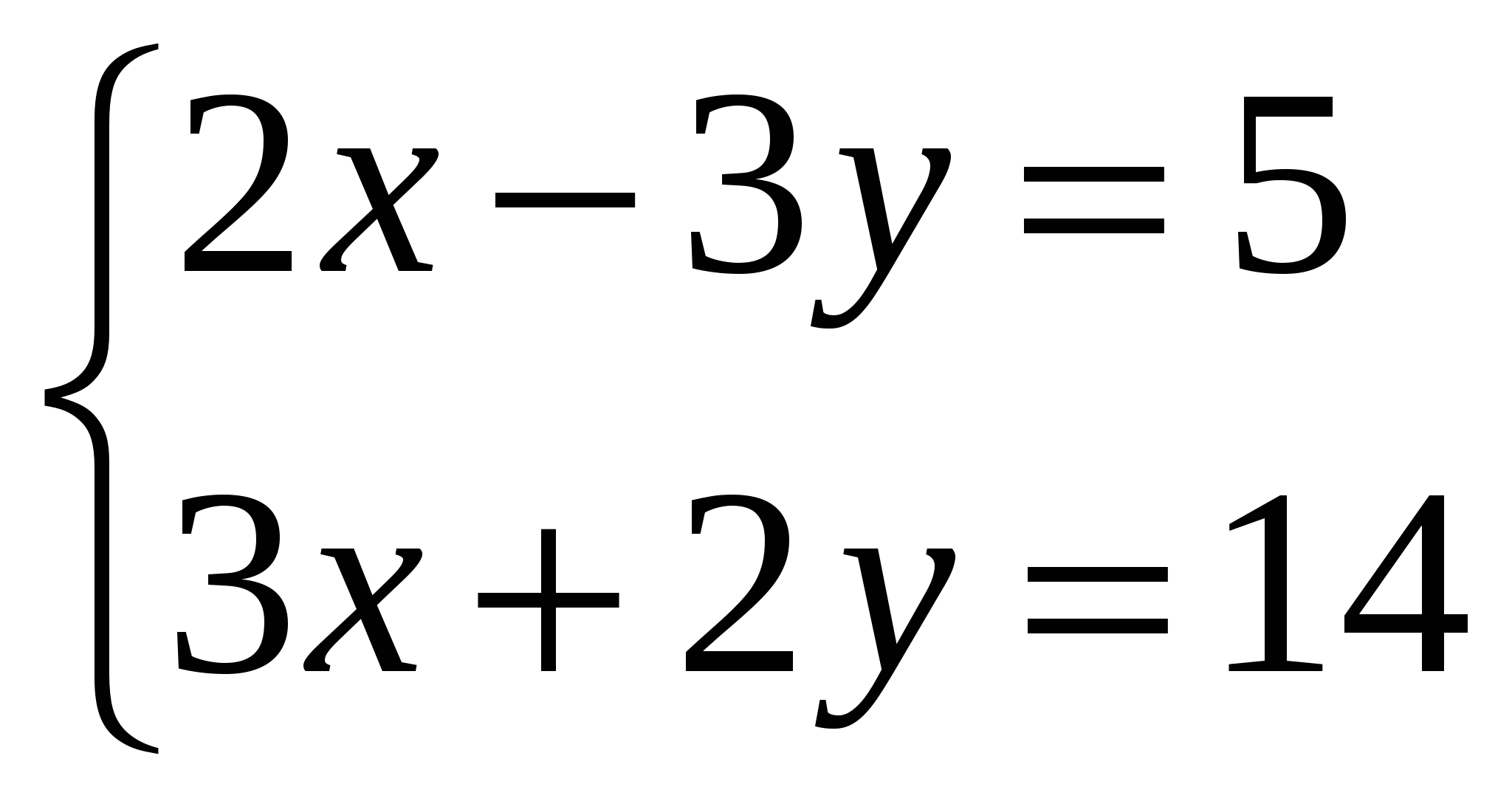
Решить систему линейных уравнений методом Крамера и методом Гаусса:
1. 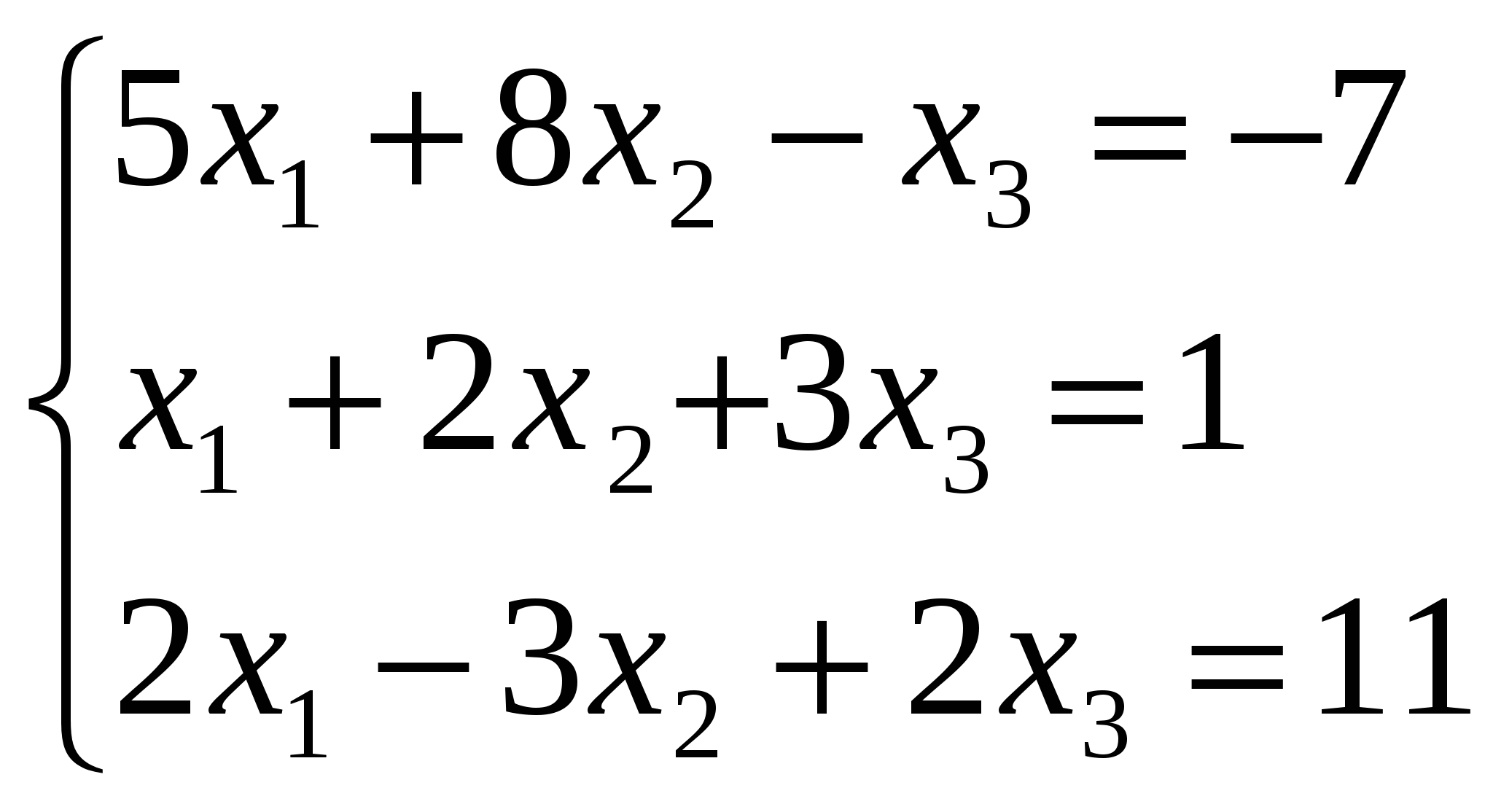 3.
3. 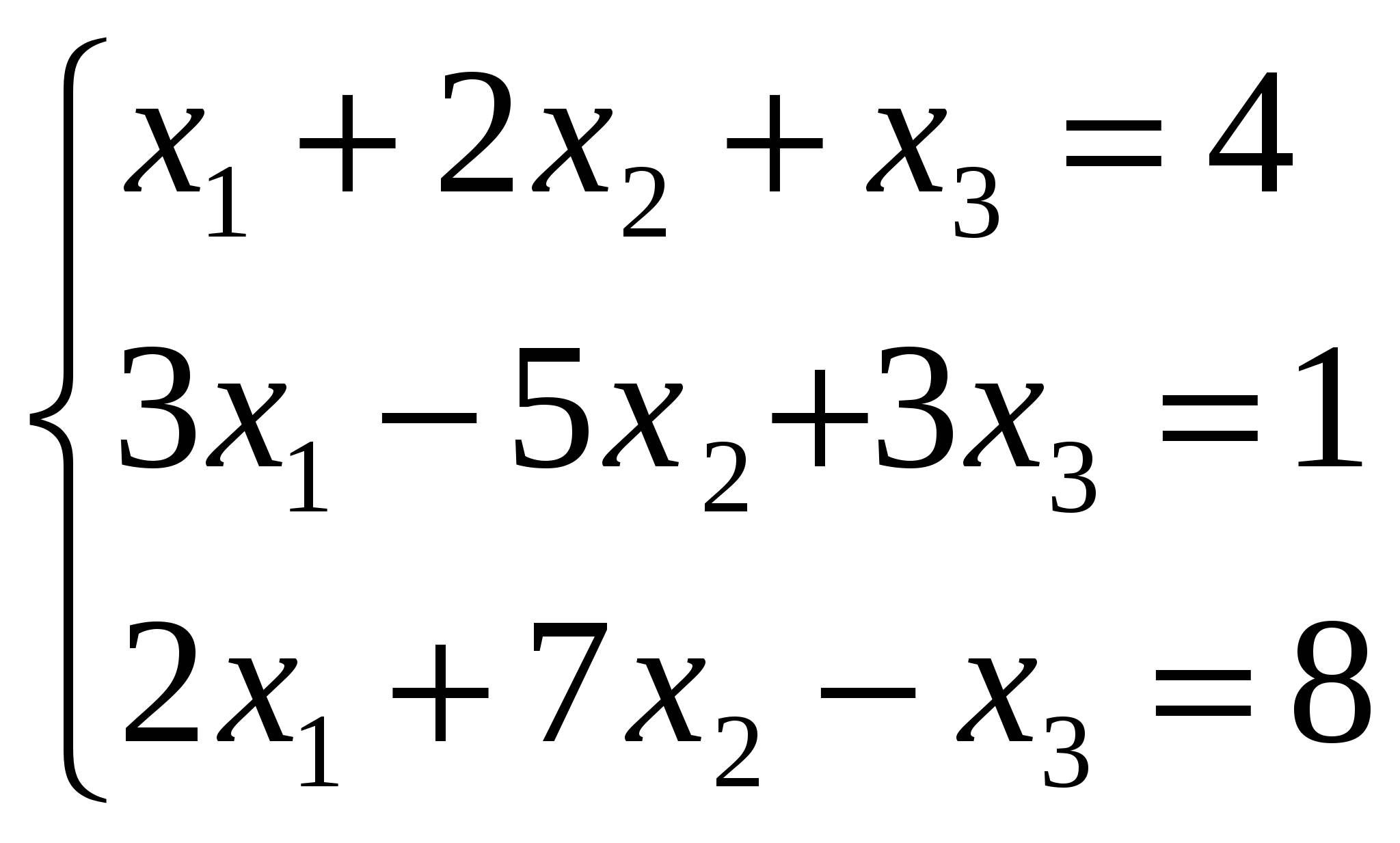
2. 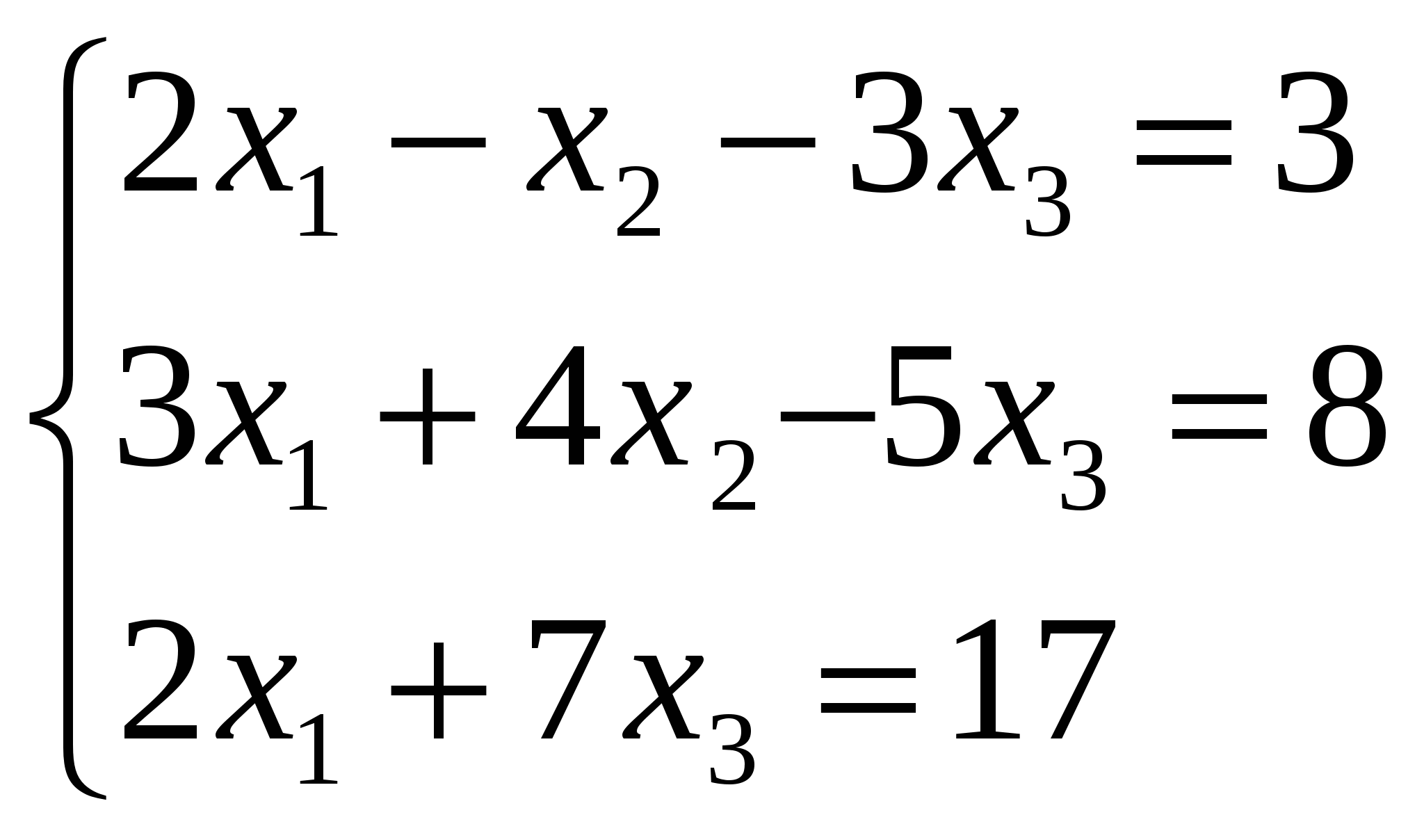 4.
4. 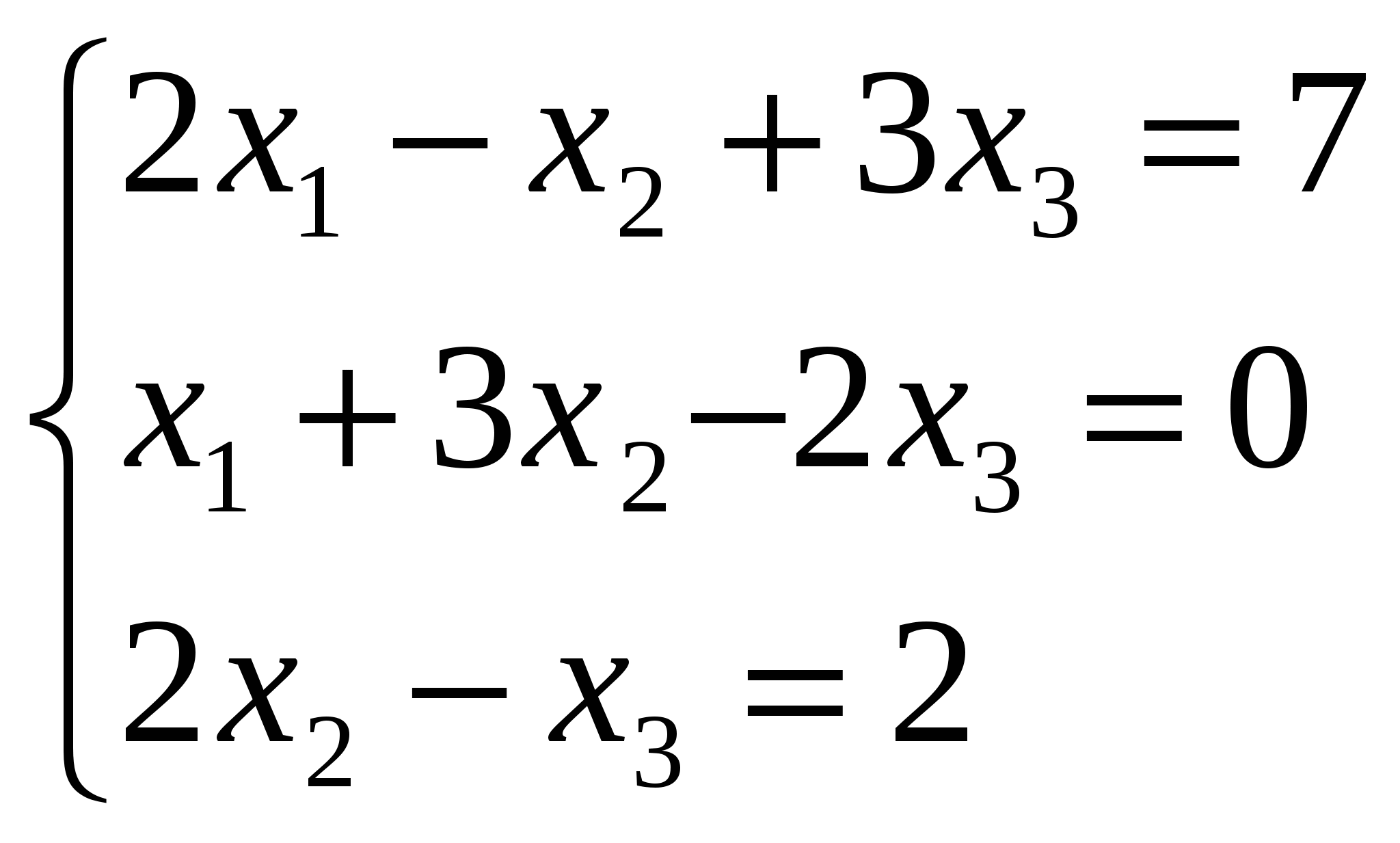
Решить систему неравенств:
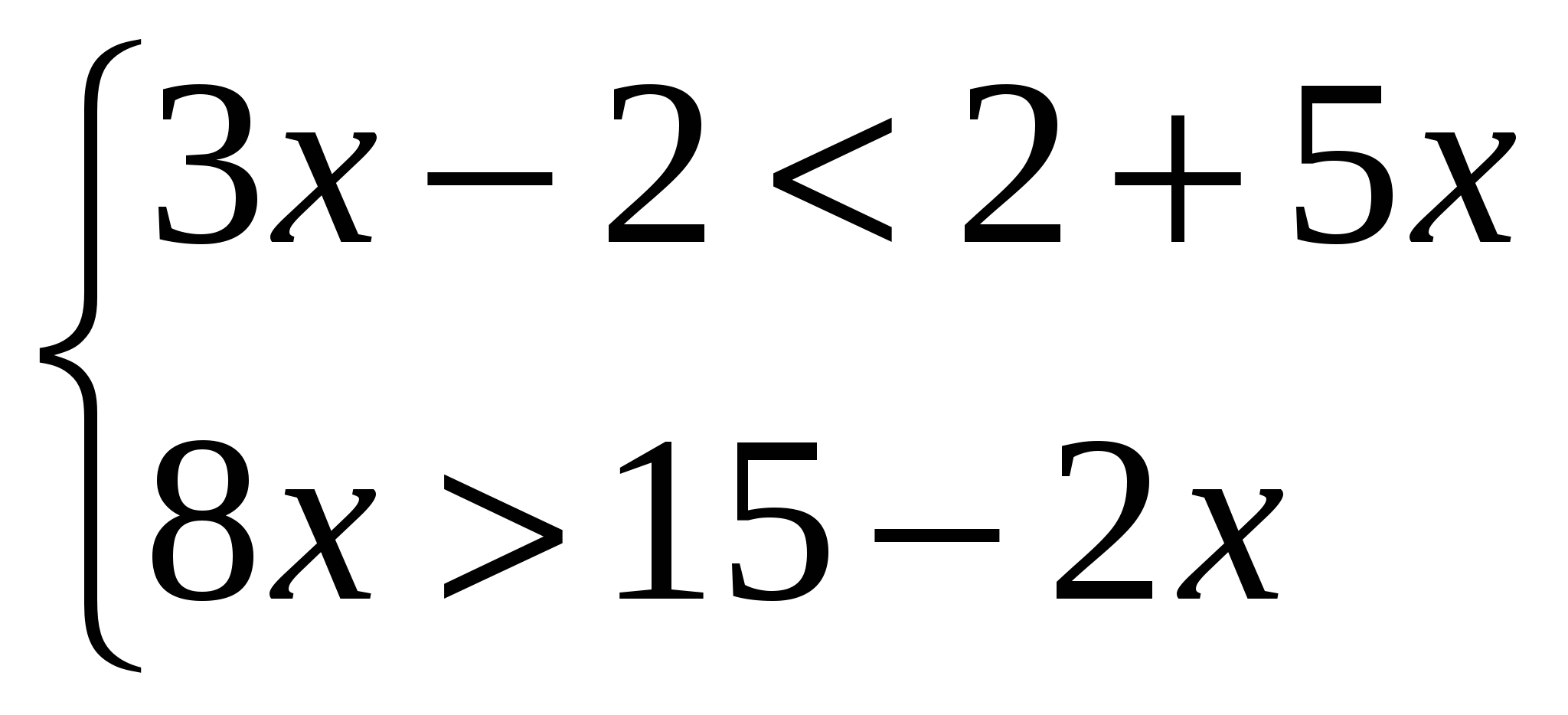
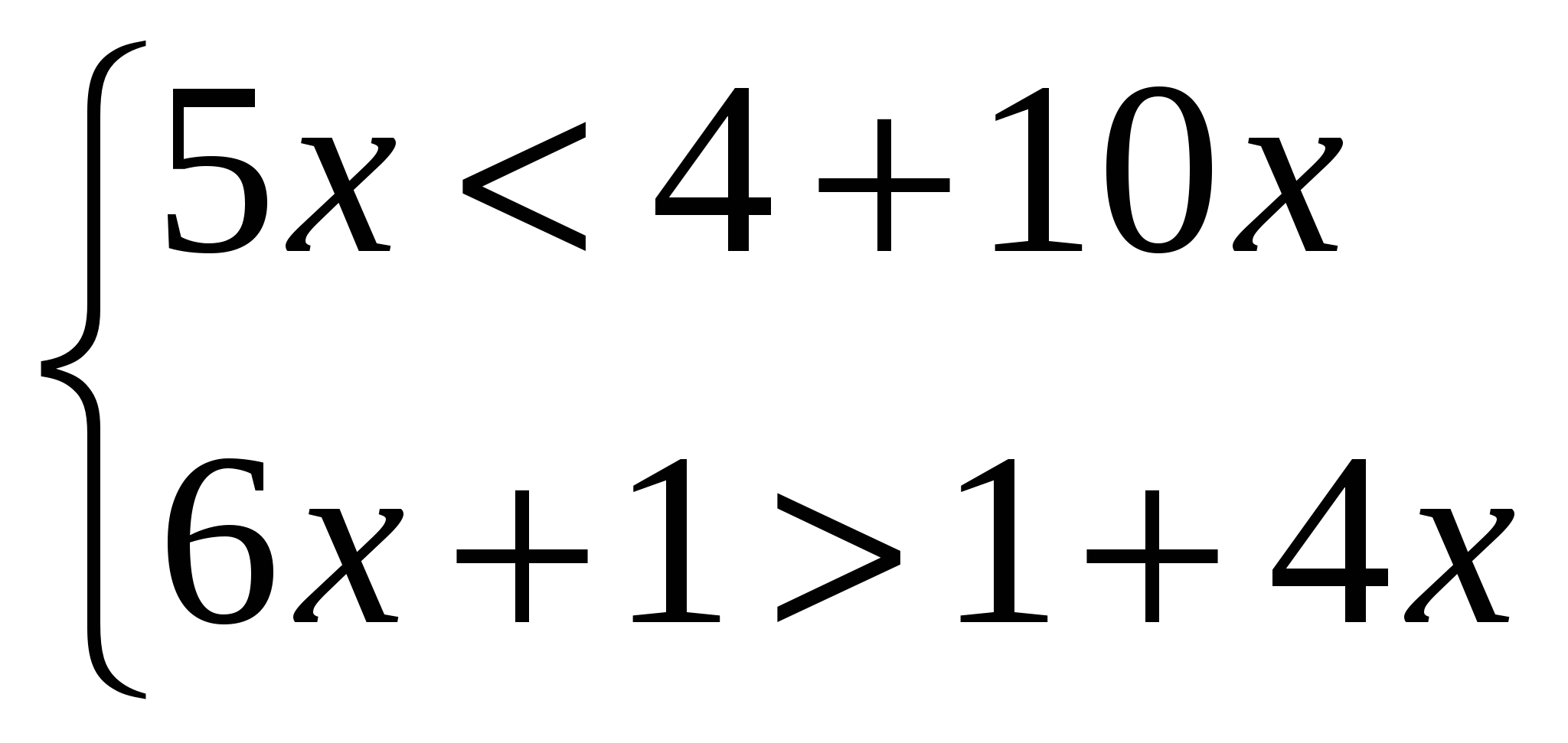
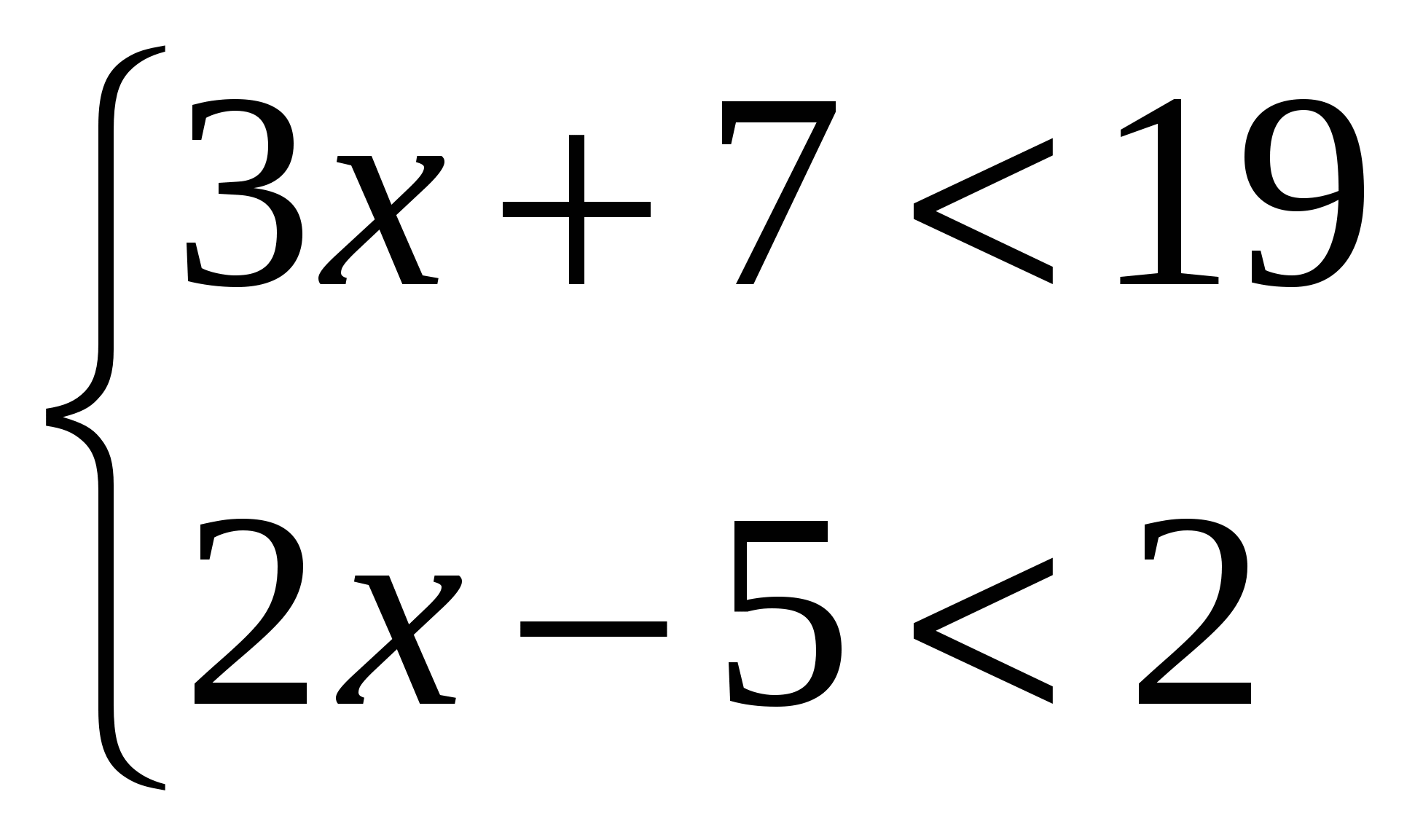
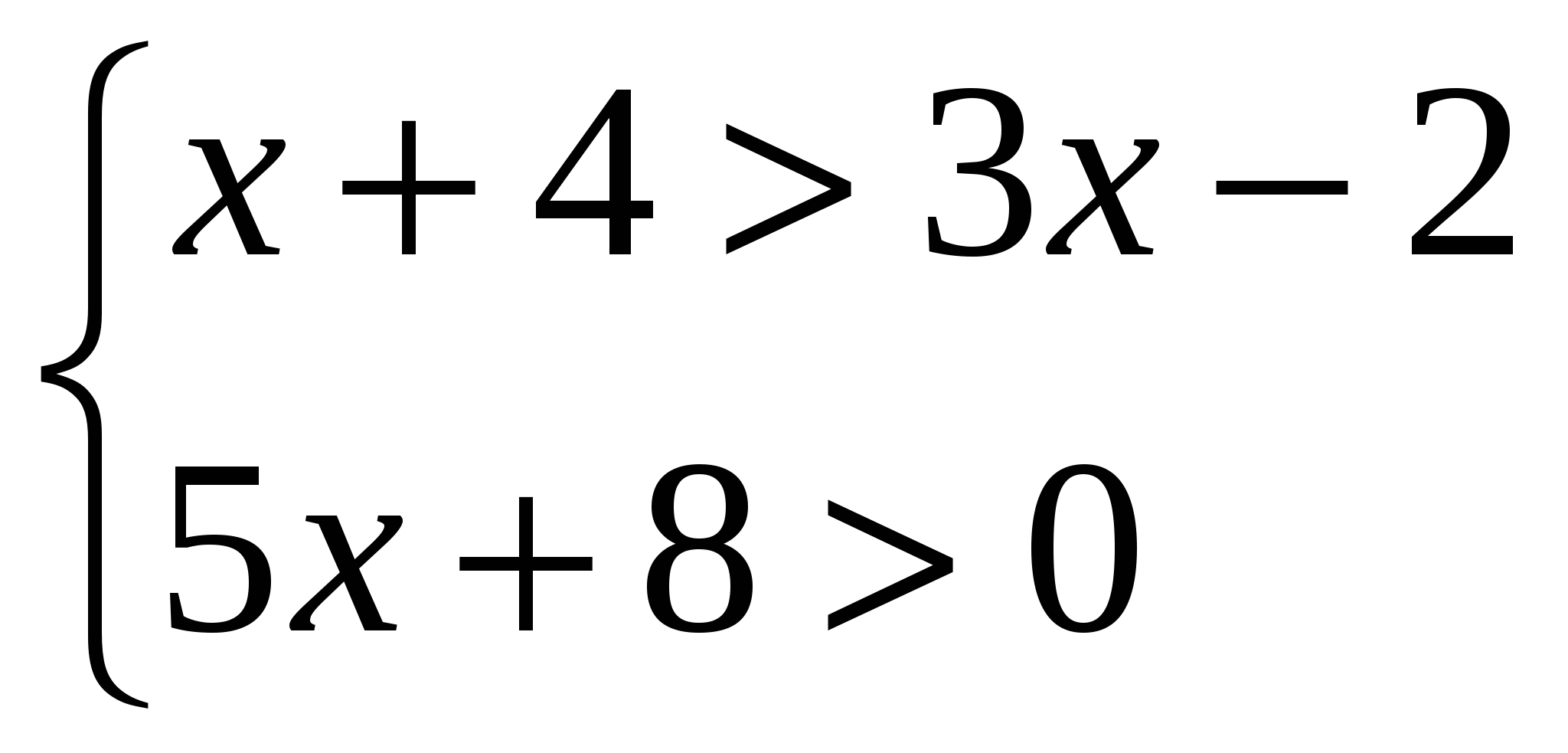
Найдите значение выражения
![]() , при
, при ![]() .
.
![]() , при
, при ![]() .
.
![]() , при
, при ![]() .
.
![]() , при
, при ![]() .
.
![]() , при
, при ![]() .
.
![]() , при
, при ![]() .
.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ САРАТОВСКОЙ ОБЛАСТИ
Государственное автономное профессиональное образовательное учреждение
Саратовской области
«Энгельсский колледж профессиональных технологий »
ВАРИАНТЫ ЭКЗАМЕНАЦИОННЫХ ТЕСТОВ
по дисциплине
«МАТЕМАТИКА»
(цикл общеобразовательный дисциплин)
для студентов 1 курса дневного отделения
Вариант 1
При выполнении задания 1 – 11 в бланках ответа под номером соответствующего задания, поставьте номер правильного ответа.
-
Какое из указанных чисел является значением выражения
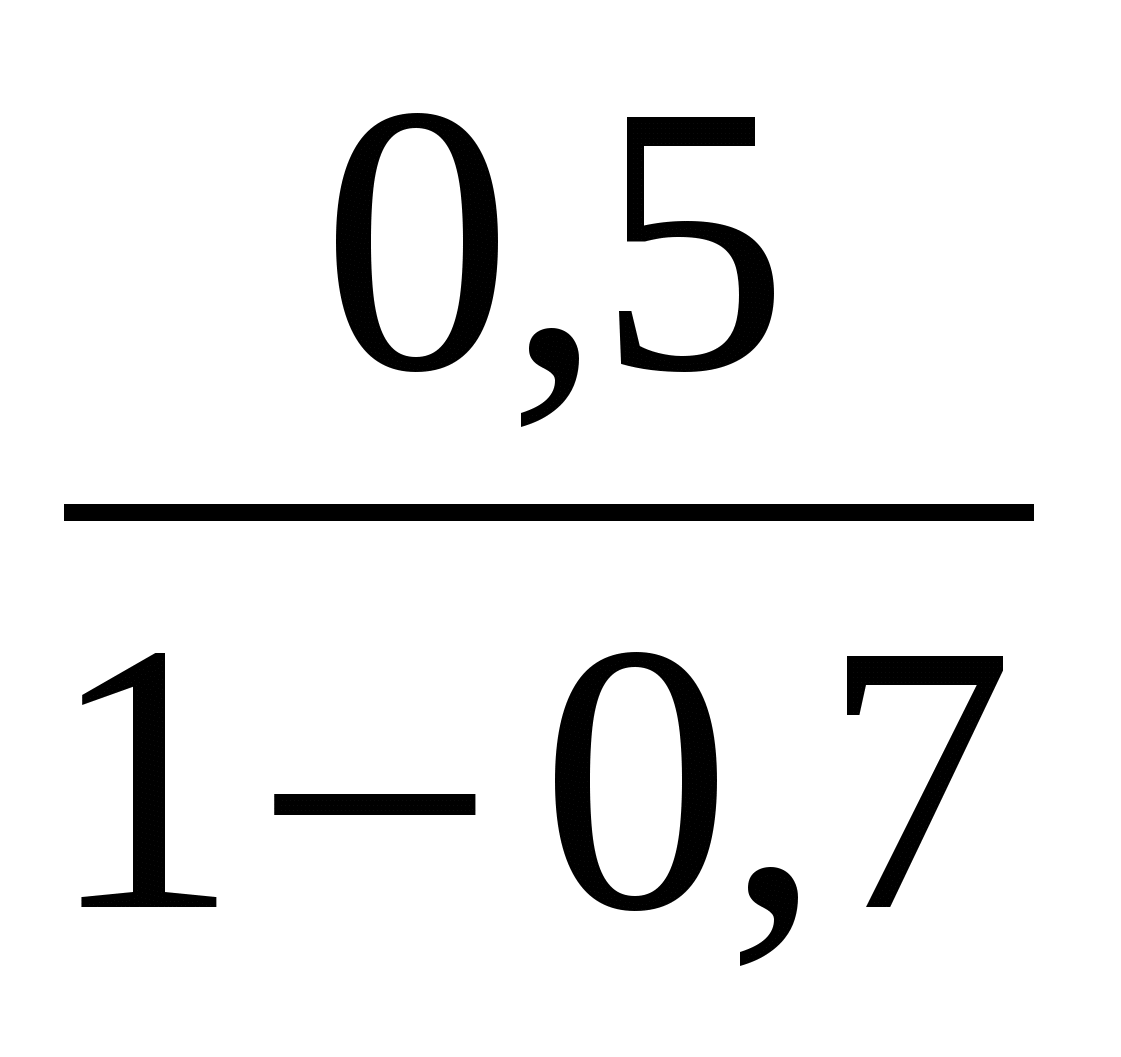 ?
?
1) ![]() 2) 1,2 3) 1,5 4)
2) 1,2 3) 1,5 4)![]()
-
Билет на автобус стоит 15 рублей. Какое максимальное число билетов можно купить на 100 рублей после повышения цены на 20%?
1) 4 2) 6 3) 5 4) 7
-
Найдите
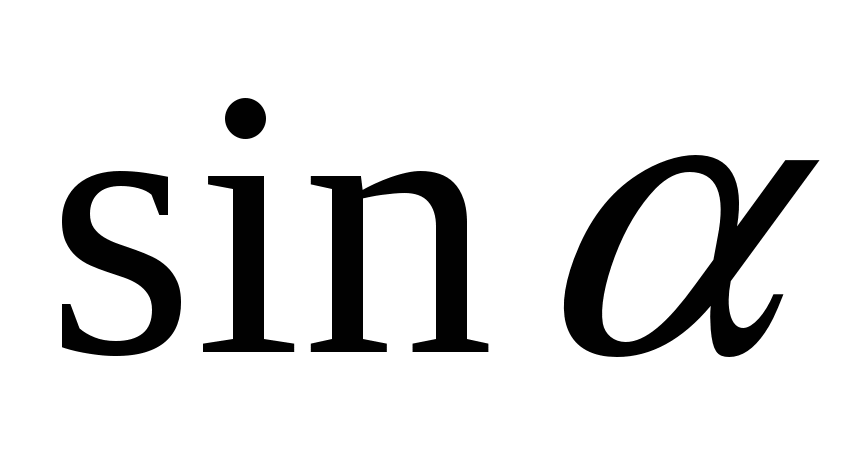 , если
, если 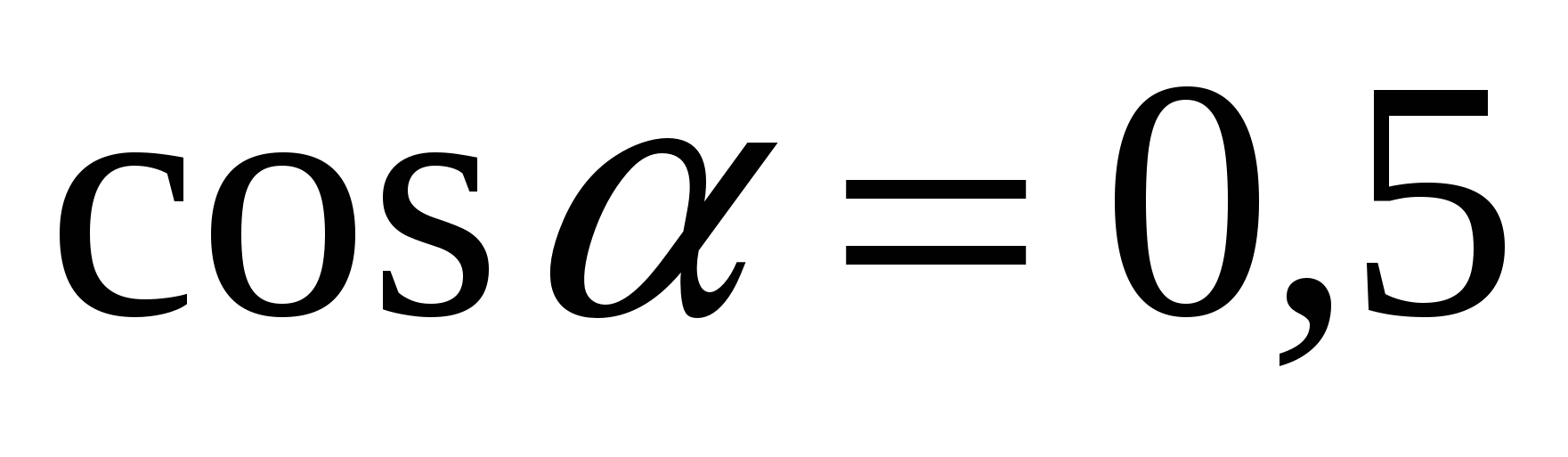 ,
, 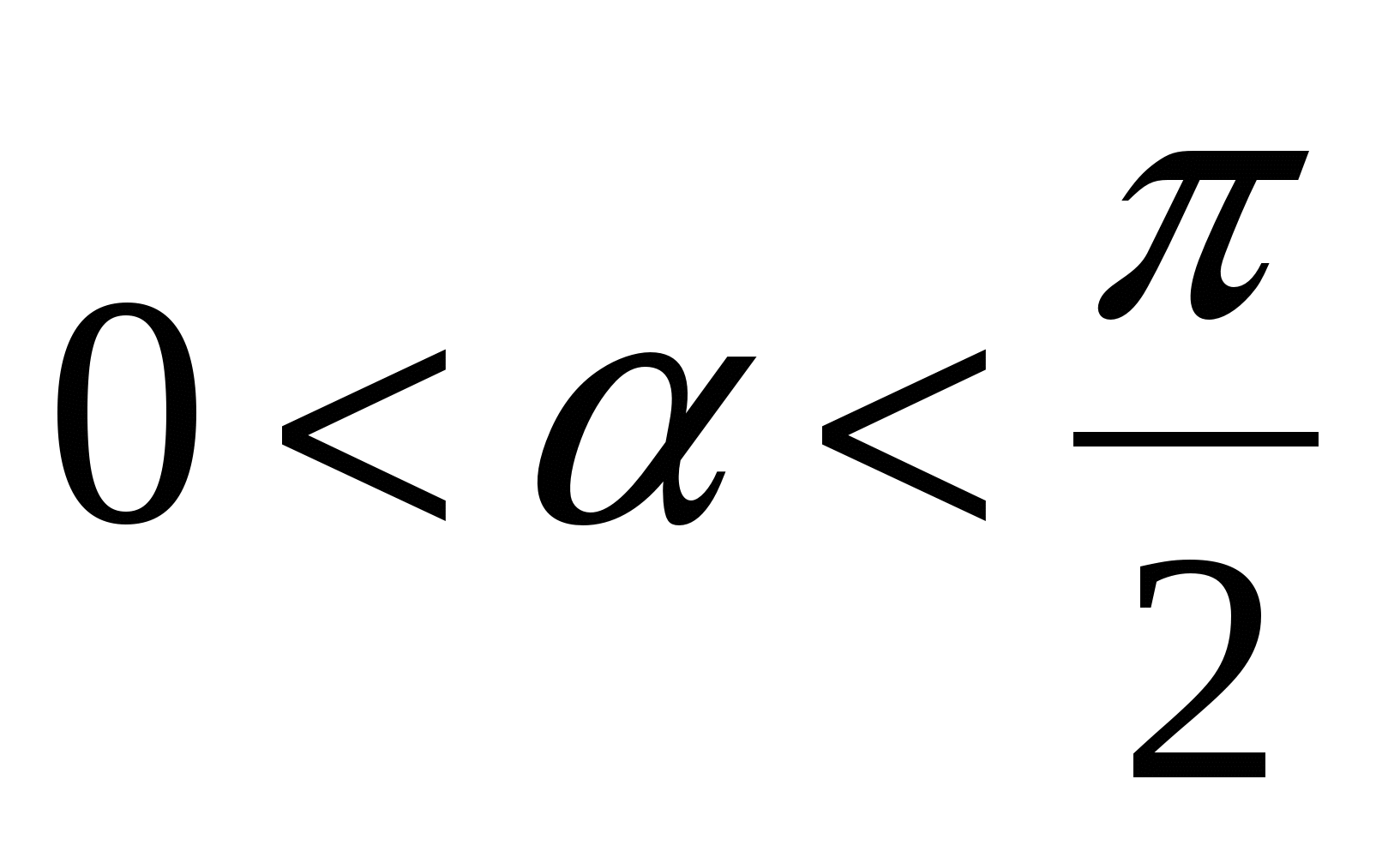 .
.
1) ![]() 2) 0 3)
2) 0 3) ![]() 4) 1
4) 1
-
В сборнике по биологии всего 25 билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достается один случайно выбранный билет из этого сборника. Какова вероятность того, что в этом билете не будет вопроса о грибах?
1) 0,92 2) 0,08 3) 0,80 4) 0,25
-
Упростите выражение и выберите правильный ответ
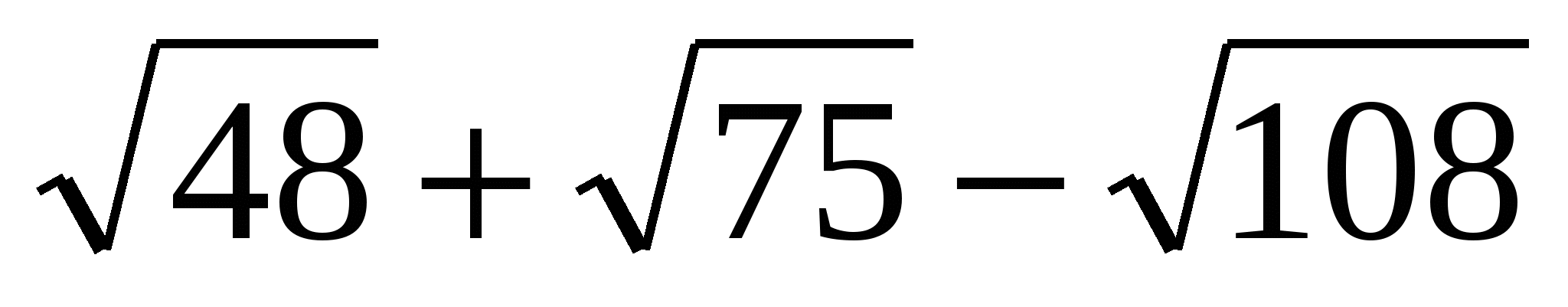 .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
-
Определите угловой коэффициент прямой
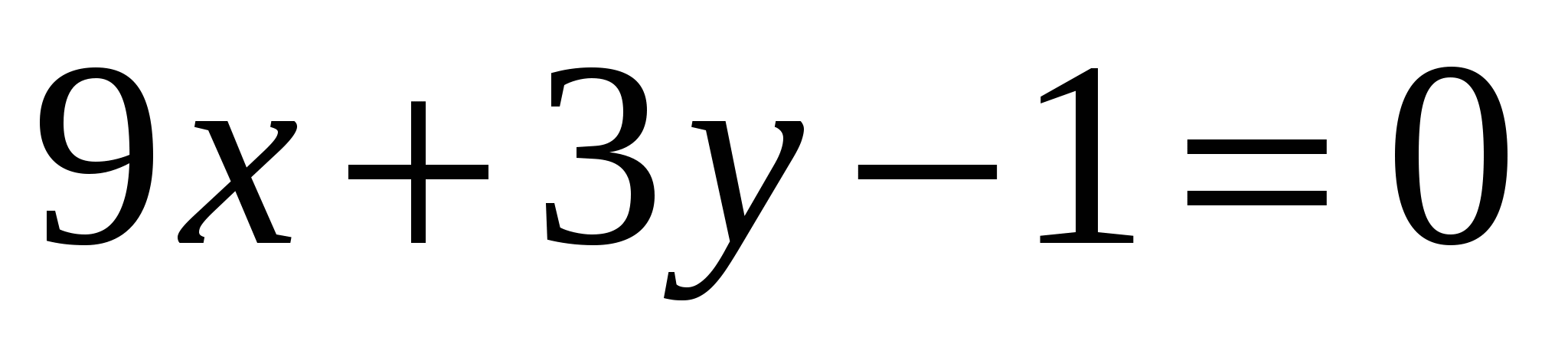 .
.
1) 9 2) ![]() 3) – 3 4)
3) – 3 4)![]()
-
Предел функции
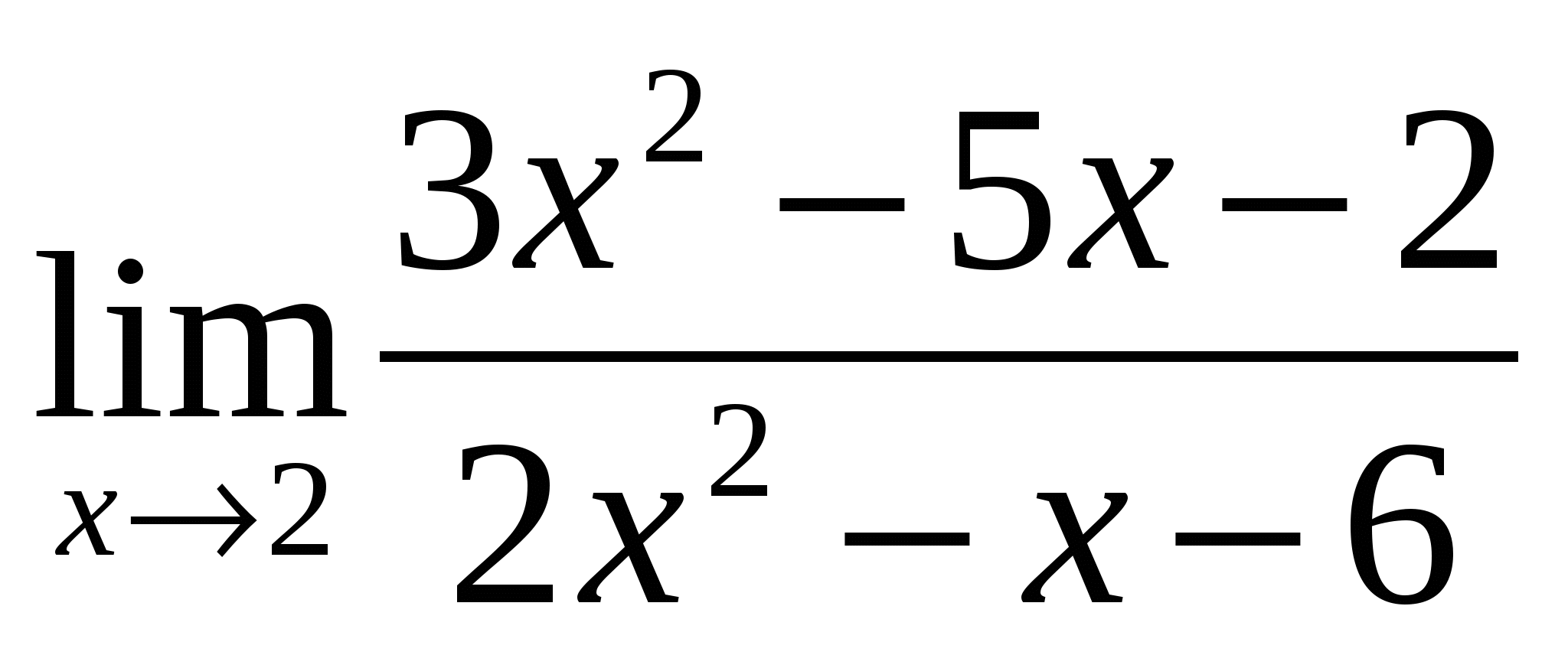 равен:
равен:
1) 0 2) 1 3) ![]() 4)
4) ![]()
-
Объем первого цилиндра равен 12 см3. Найдите объем второго цилиндра, если при равных диаметрах, его высота в три раза больше, чем у первого.
1) 36 2) 15 3) 117 4) 48
-
Площадь полной поверхности куба равна 54 см2. Найдите длину ребра.
1) 6 2) 3 3) 9 4) 13,5
-
Общее количество граней у тетраэдра равно
1) 3 2) 6 3) 5 4) 4
-
Число сочетаний 4 элементов по 3 равно
1) 4 2) 24 3) 3 4) 12
При выполнении задания 12 – 16 укажите сначала номер задания, а затем запишите его решение.
-
Вычислите значение производной заданной функции при указанном значении независимой переменной:
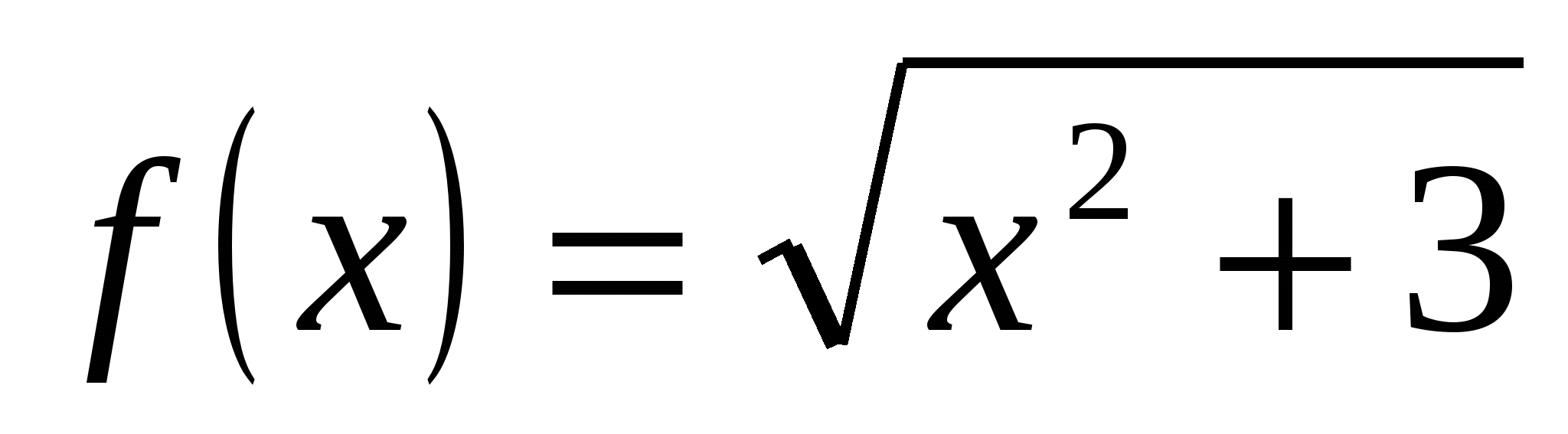 ;
; 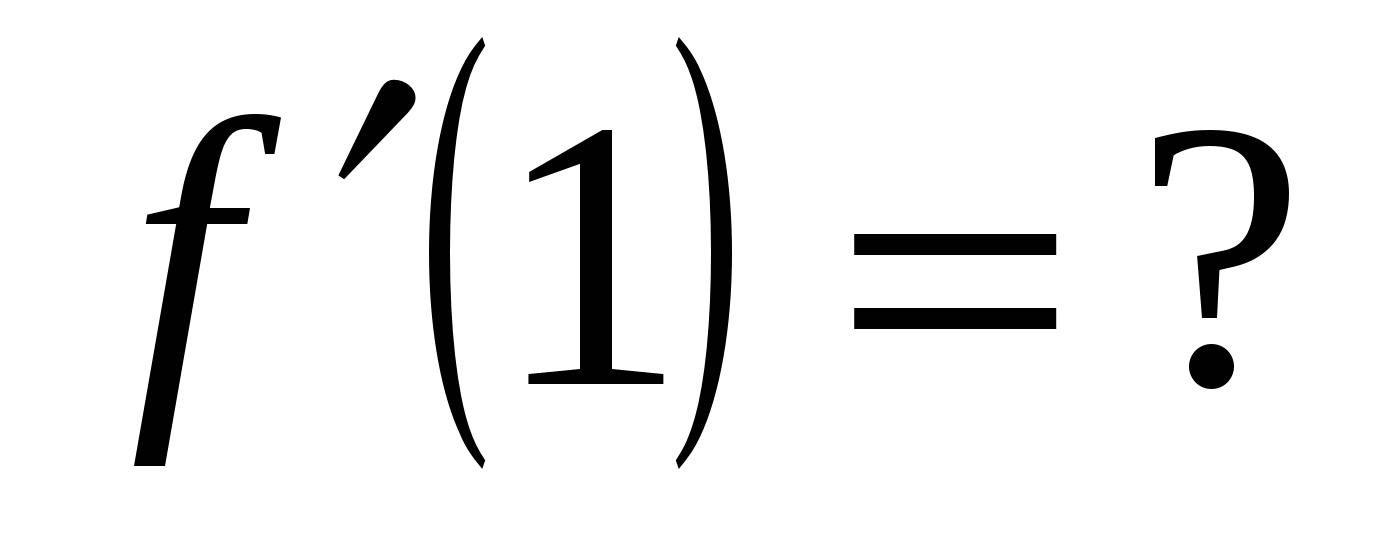
-
Найдите промежутки монотонности для функции
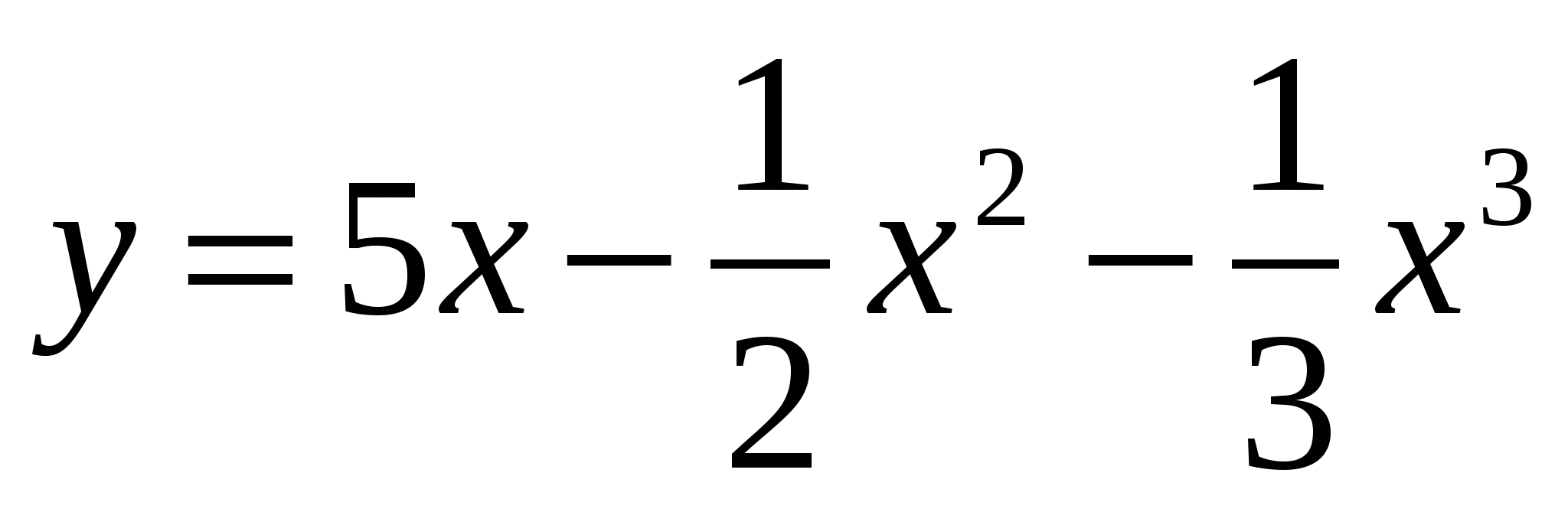 .
. -
Вычислите площадь фигуры, ограниченной заданными линиями
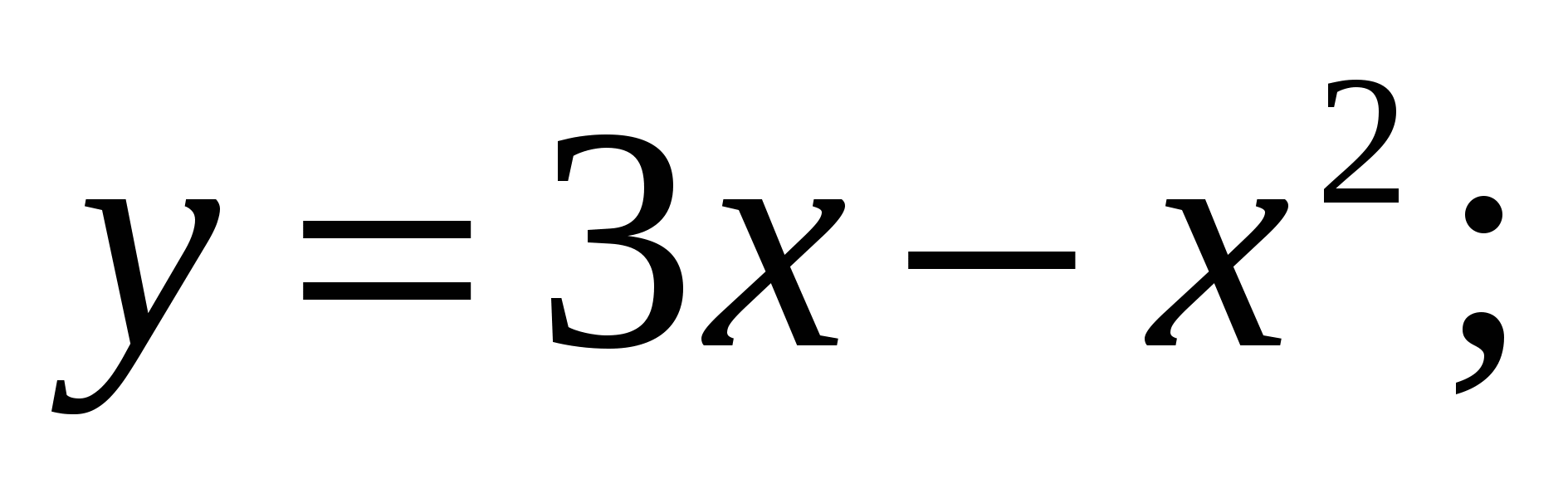
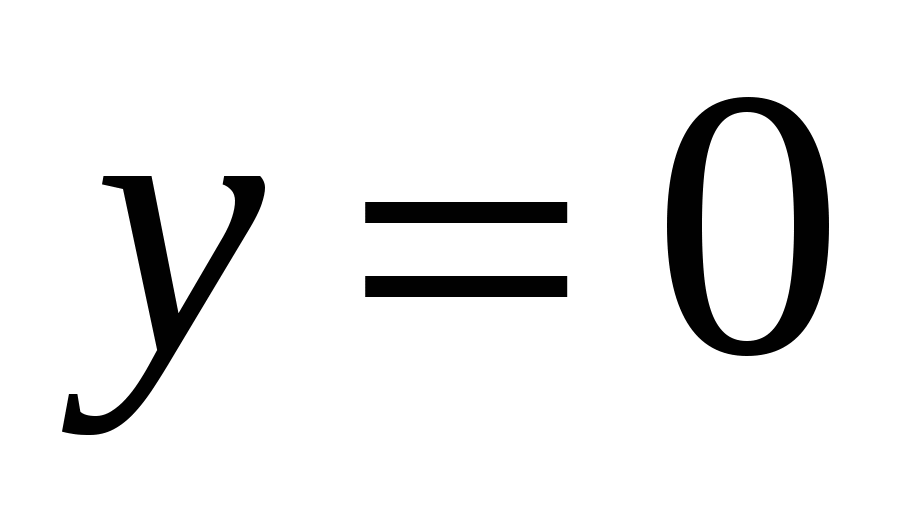 .
. -
Найдите значение выражения
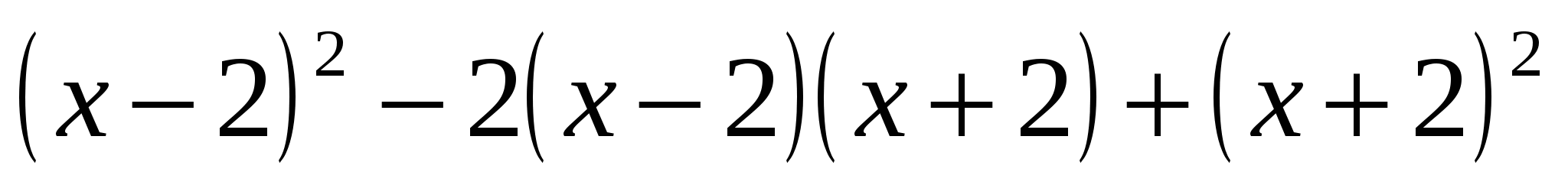 , при
, при 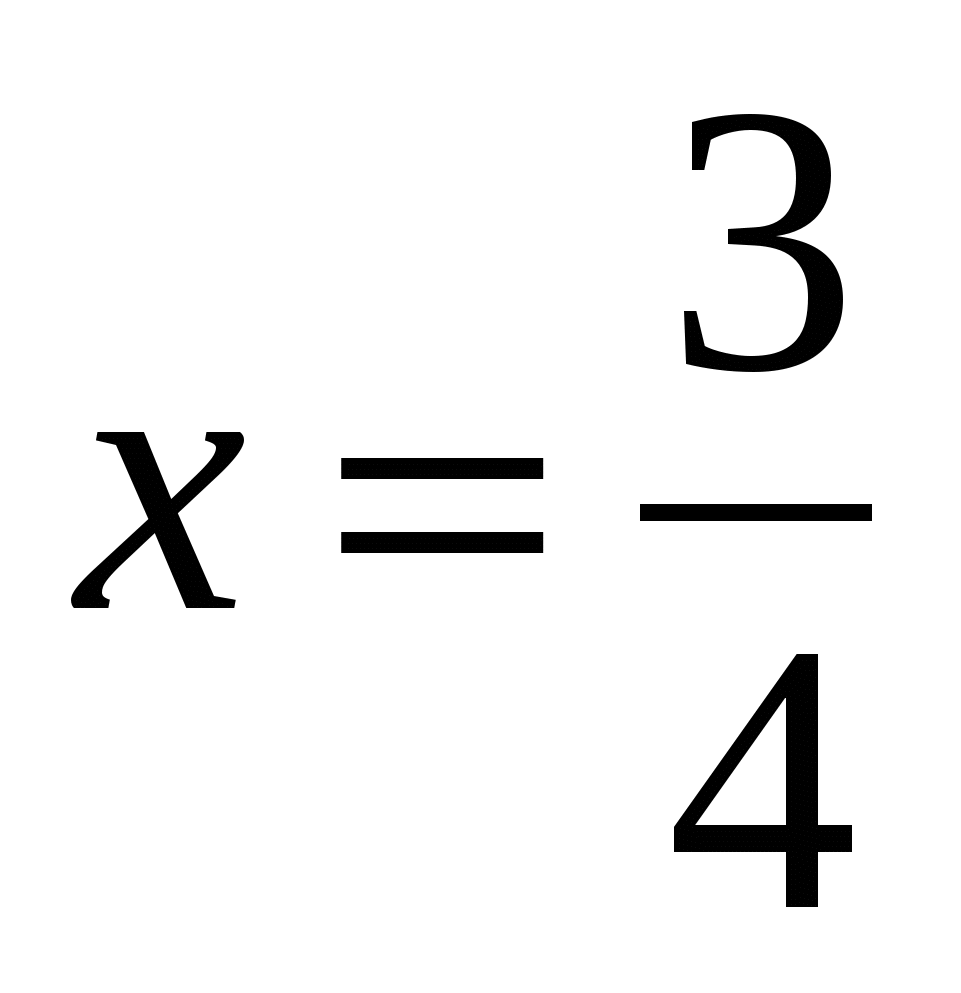 .
. -
Решите систему линейных уравнений методом Гаусса:
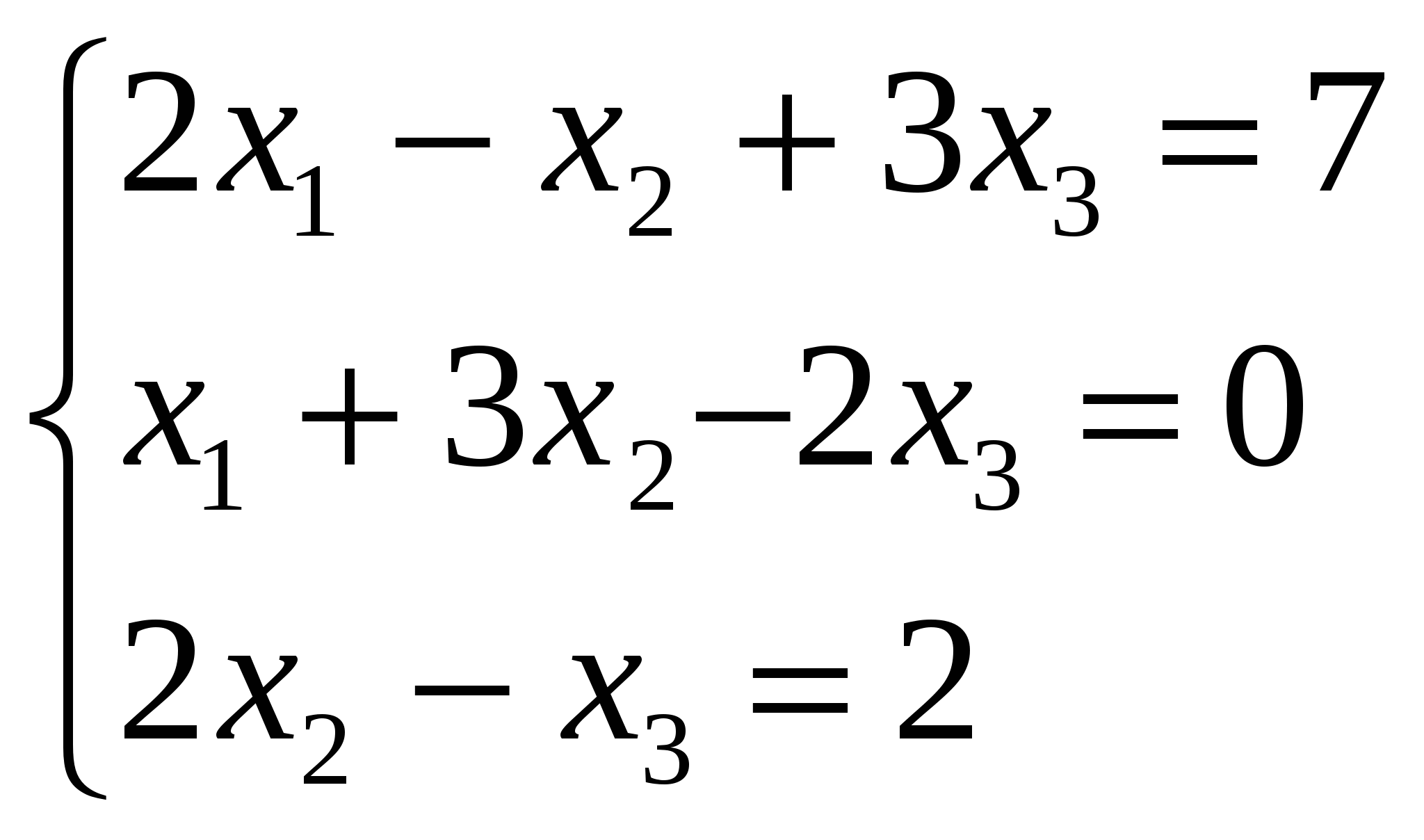
Вариант 2
При выполнении задания 1 – 11 в бланках ответа под номером соответствующего задания, поставьте номер правильного ответа.
-
Какое из указанных чисел является значением выражения
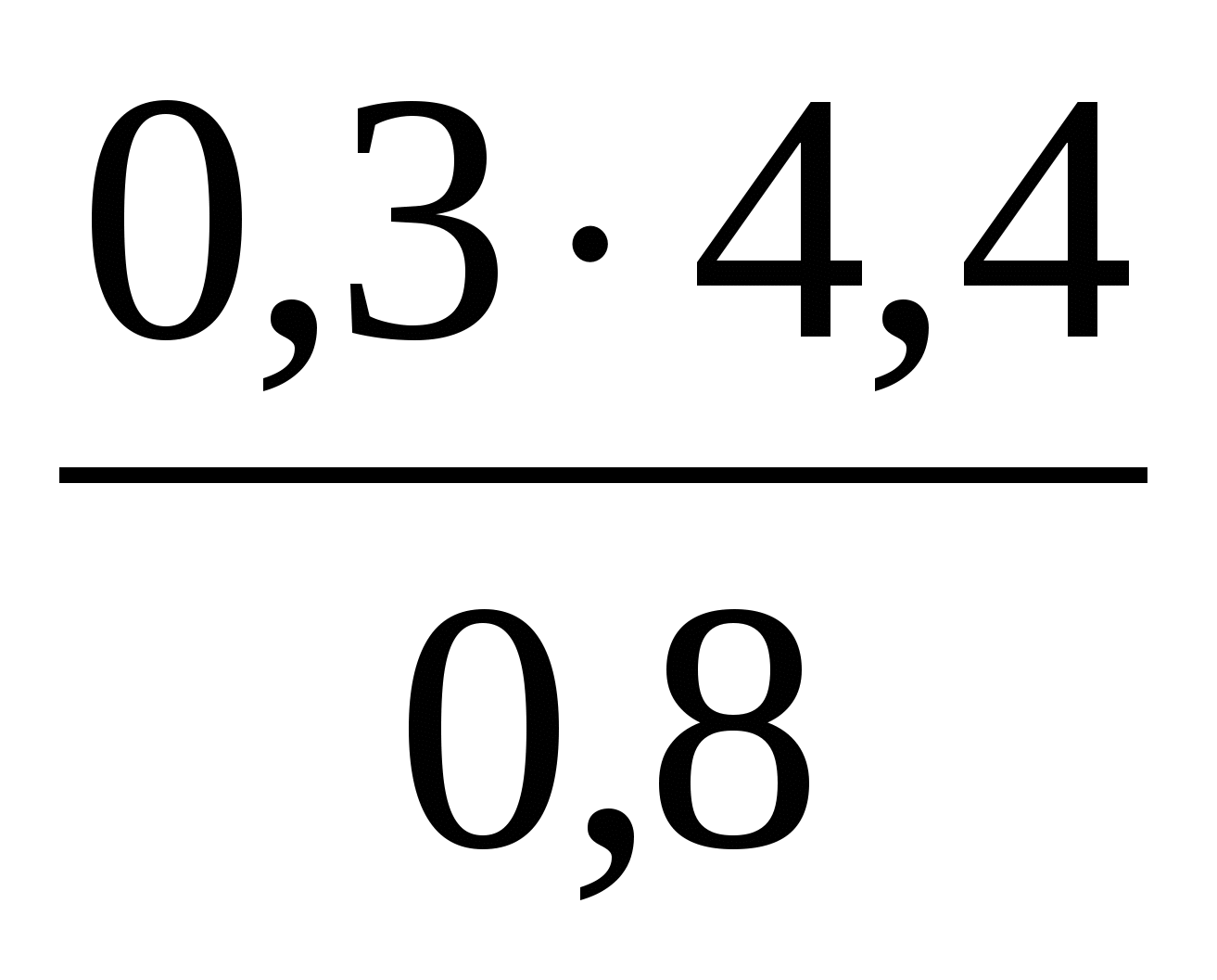 ?
?
1) 16,5 2) 5,5 3) 0,66 4) 1,65
-
Билет в кино стоит 50 рублей. Какое максимальное число билетов можно купить на 200 рублей после повышения цены на 20%?
1) 4 2) 6 3) 3 4) 5
-
Найдите
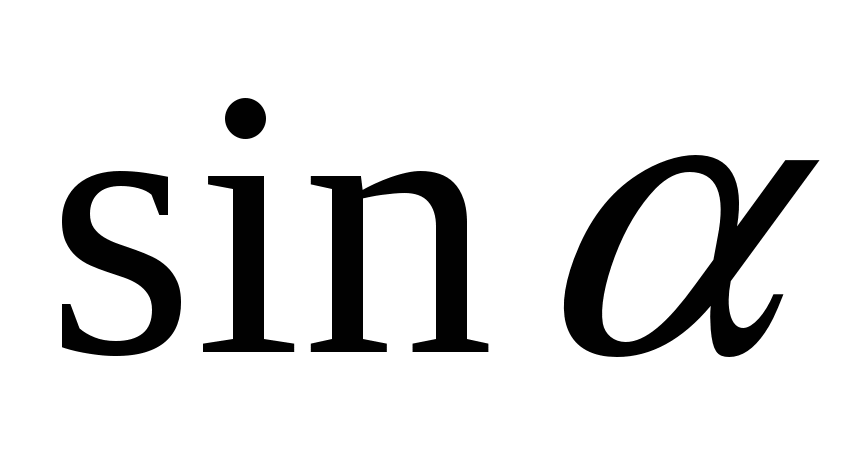 , если
, если 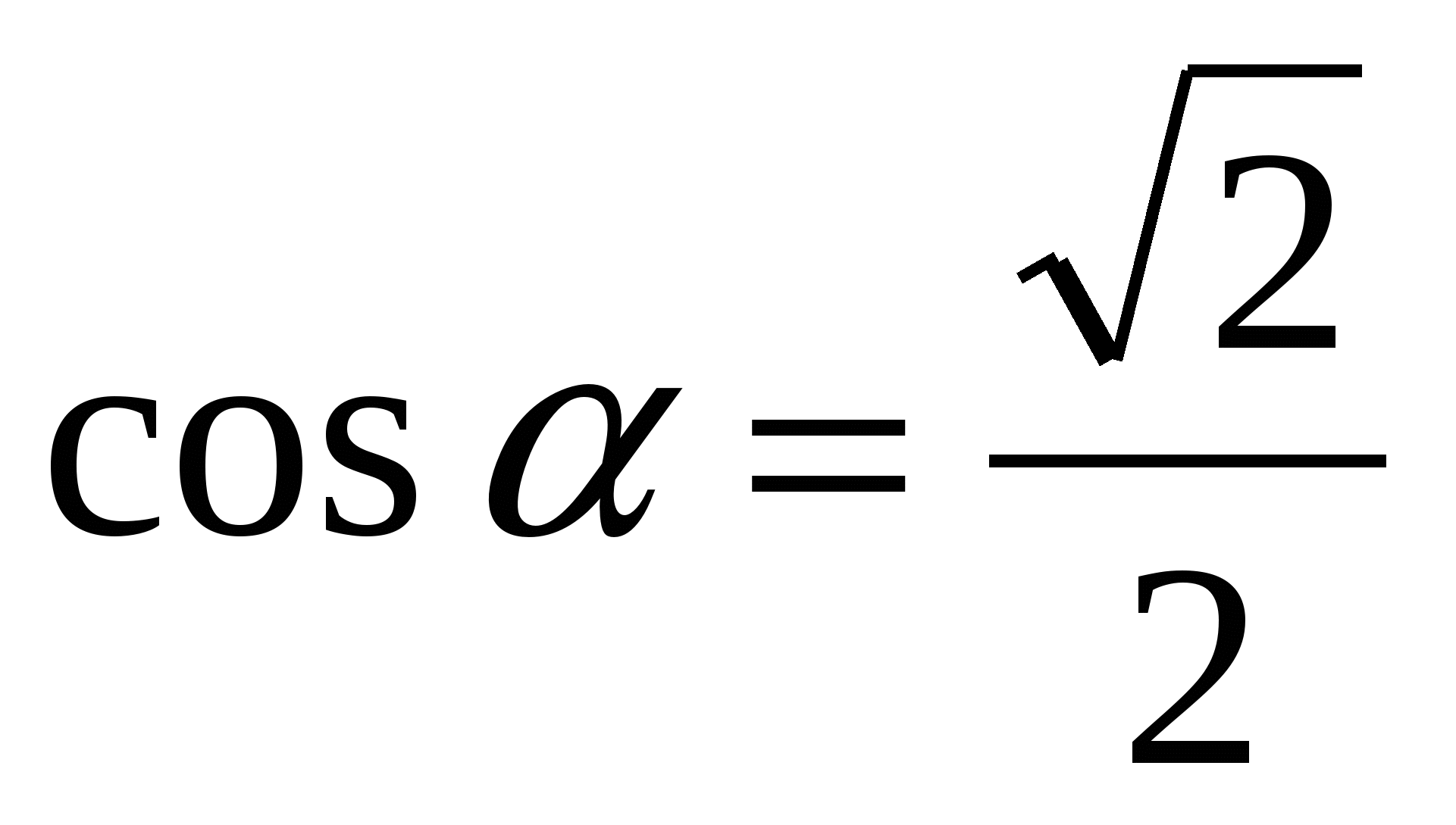 ,
, 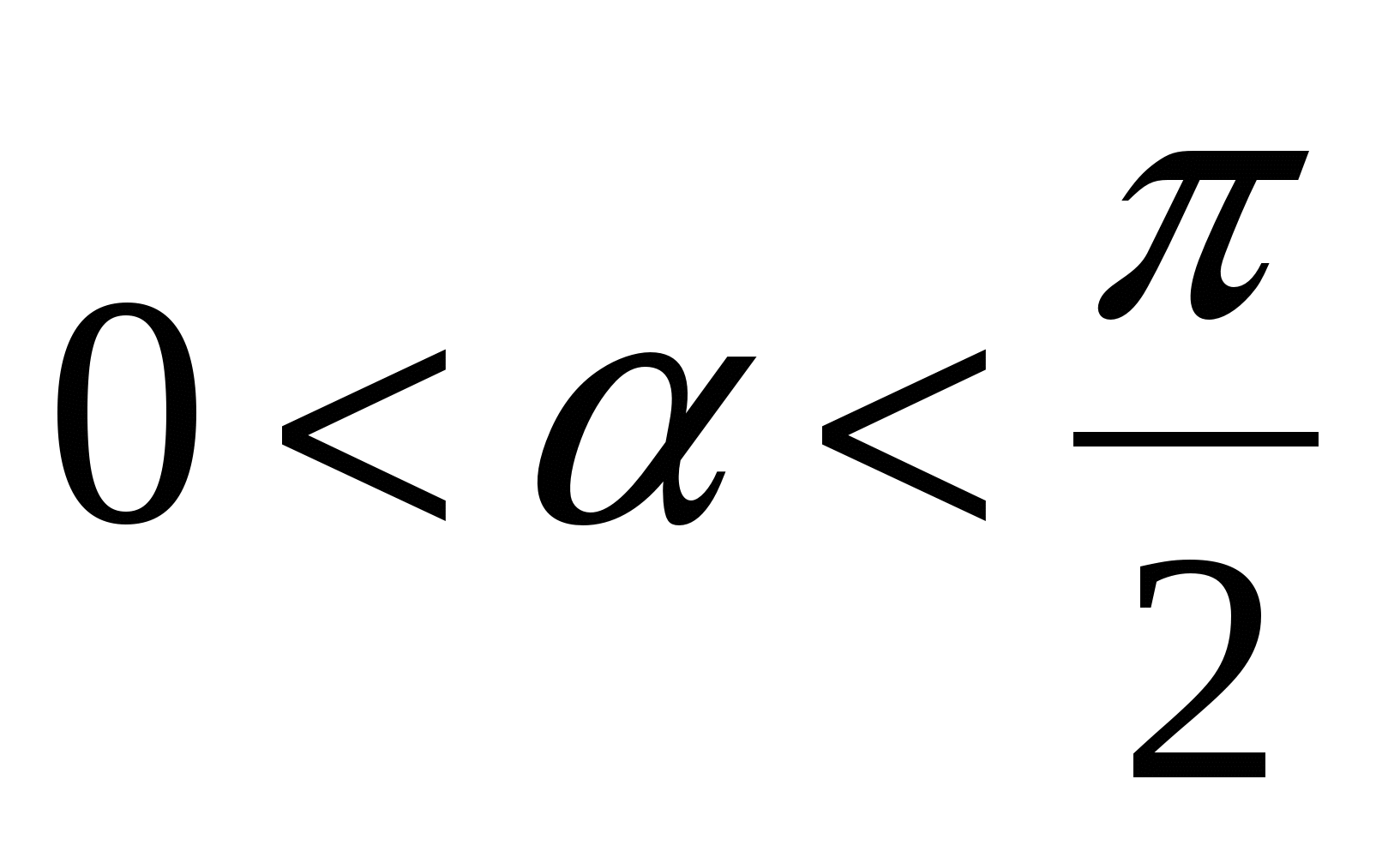 .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4) 1
4) 1
-
В сборнике по биологии всего 30 билетов, в шести из них встречается вопрос о цветах. На экзамене школьнику достается один случайно выбранный билет из этого сборника. Какова вероятность того, что в этом билете не будет вопроса о цветах?
1) 0,2 2) 0,8 3) 0,5 4) 5
-
Упростите выражение и выберите правильный ответ
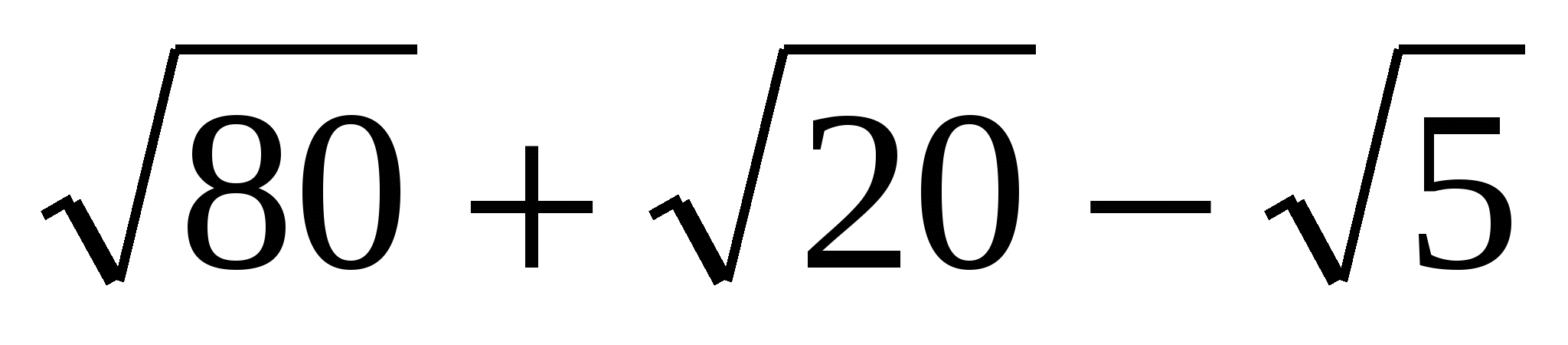 .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
-
Определите угловой коэффициент прямой
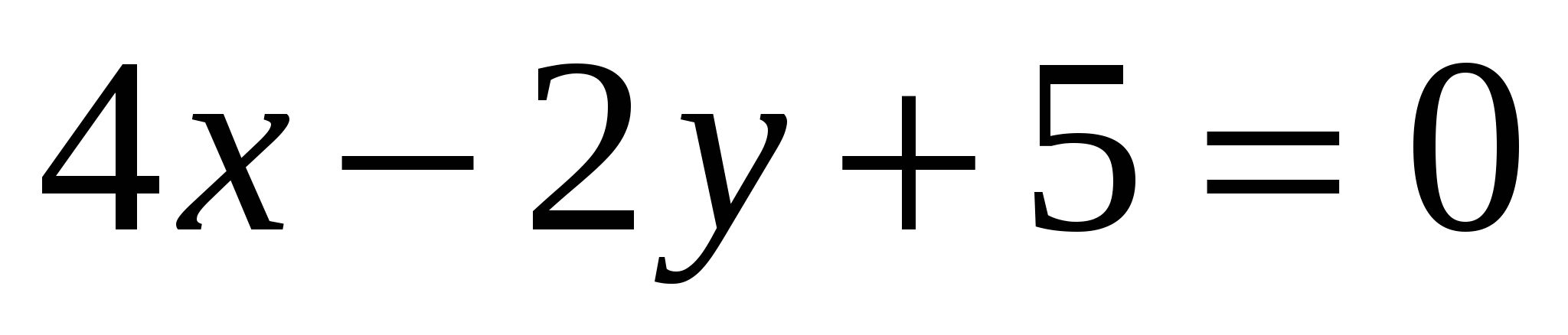 .
.
1) – 2 2) ![]() 3) 2 4)
3) 2 4)![]()
-
Предел функции
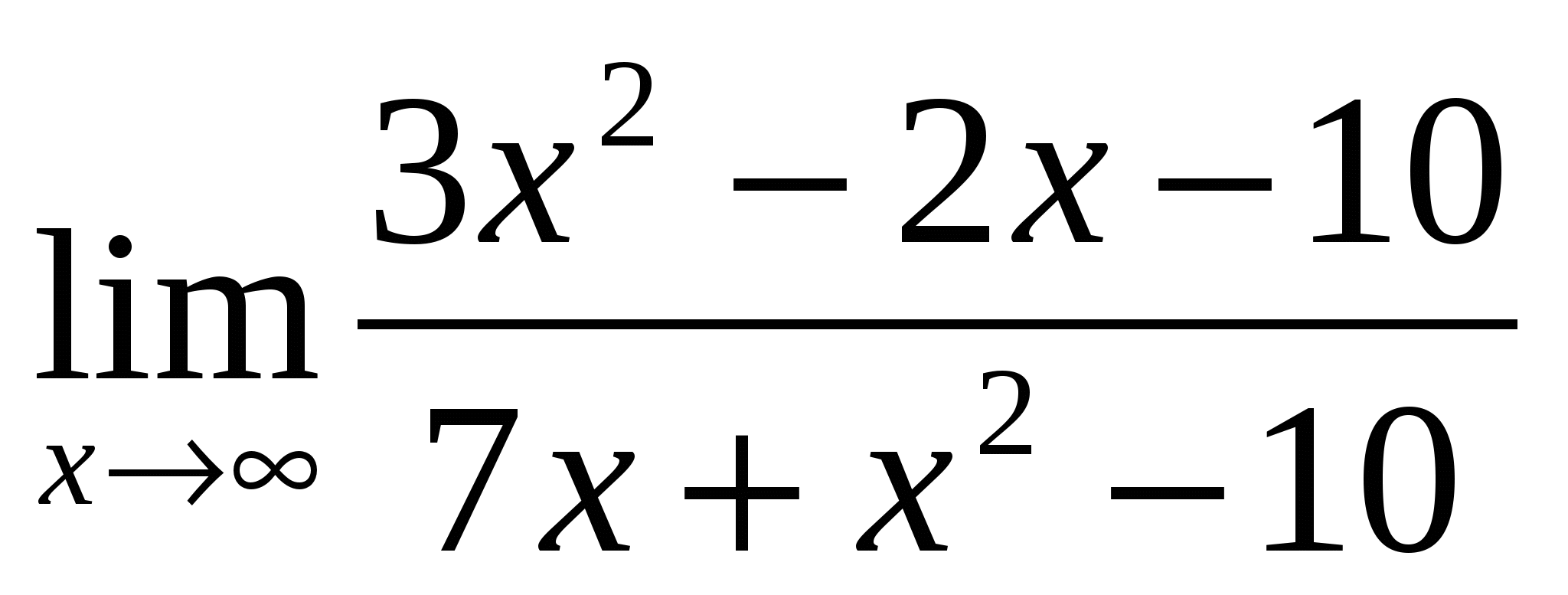 равен:
равен:
1) 3 2) 1 3) ![]() 4)
4) ![]()
-
Объем первого цилиндра равен 10 см3. Найдите объем второго цилиндра, если при равных диаметрах, его высота в два раза больше, чем у первого.
1) 2,5 2) 5 3) 40 4) 20
-
Площадь полной поверхности куба равна 96 см2. Найдите длину ребра.
1) 6 2) 4 3) 9 4) 3
-
Общее количество граней у октаэдра равно
1) 4 2) 6 3) 5 4) 8
-
Число сочетаний 5 элементов по 3 равно
1) 20 2) 30 3) 10 4) 50
При выполнении задания 12 – 16 укажите сначала номер задания, а затем запишите его решение.
-
Вычислите значение производной заданной функции при указанном значении независимой переменной:
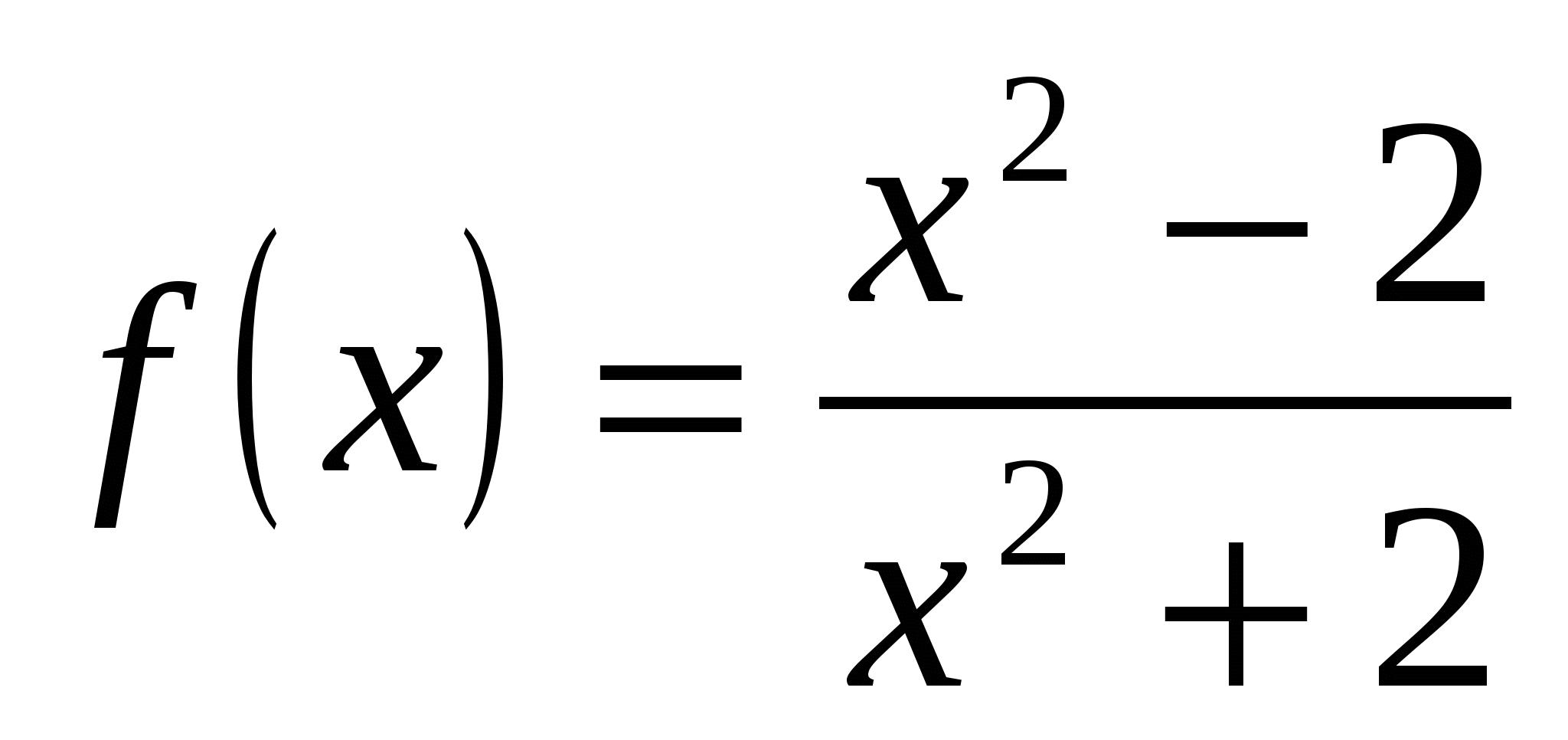 ;
; 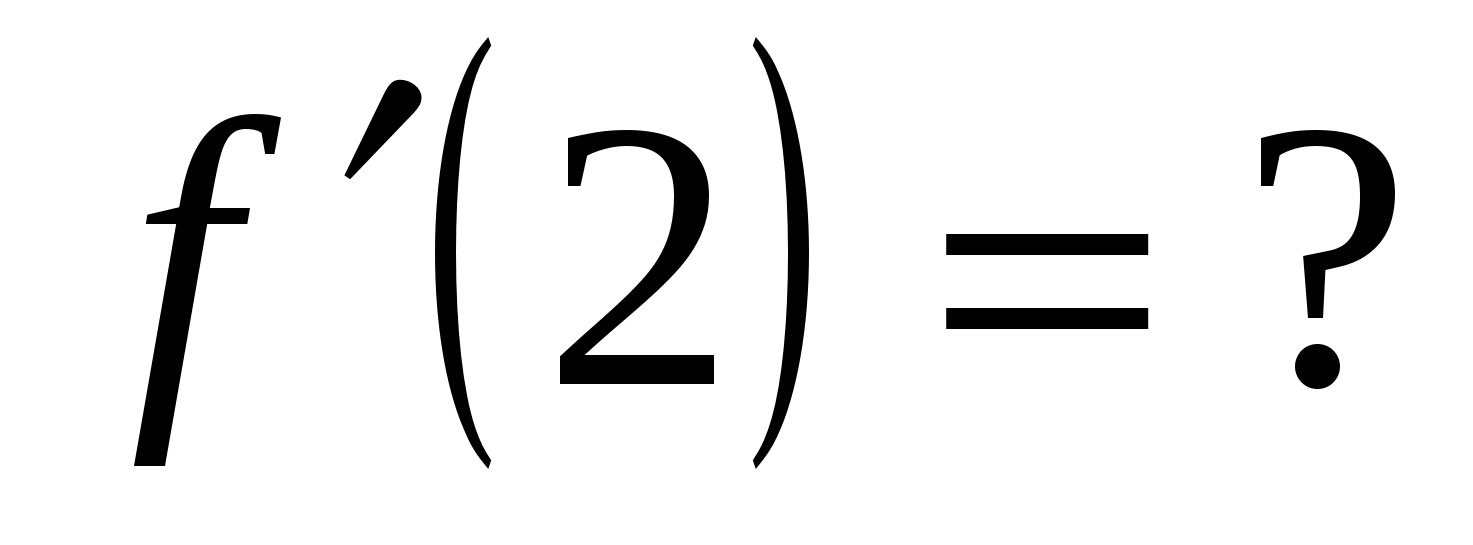
-
Найдите промежутки монотонности для функции
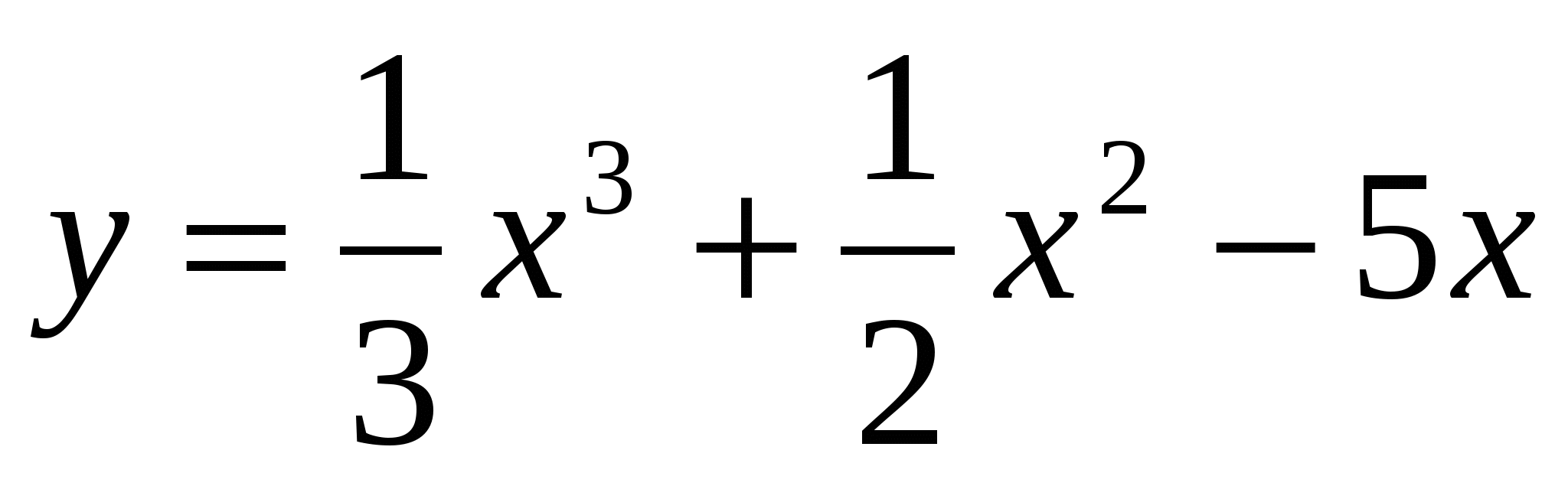 .
. -
Вычислите площадь фигуры, ограниченной заданными линиями
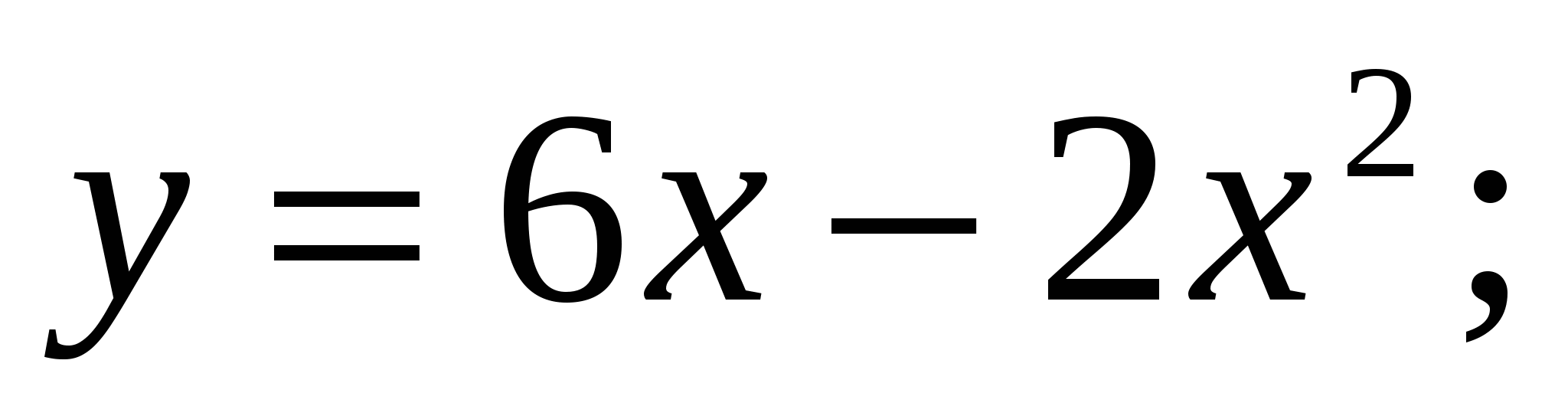
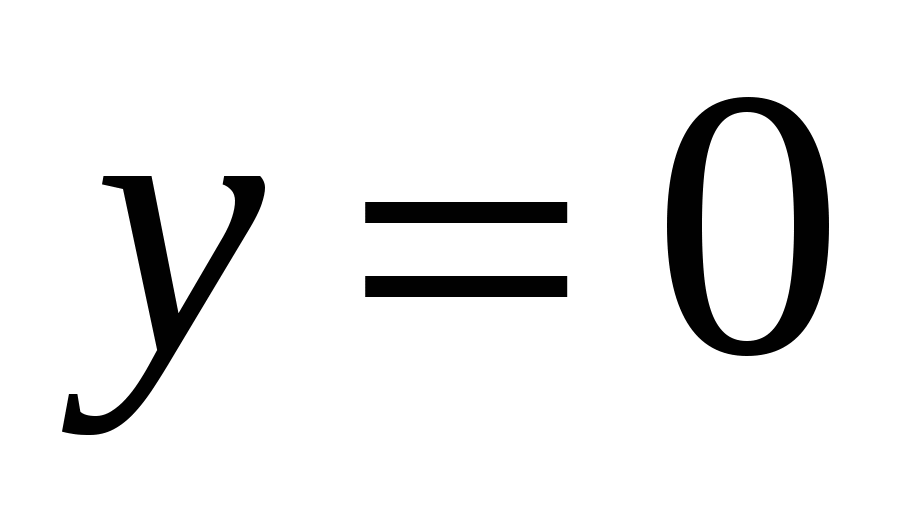 .
. -
Найдите значение выражения
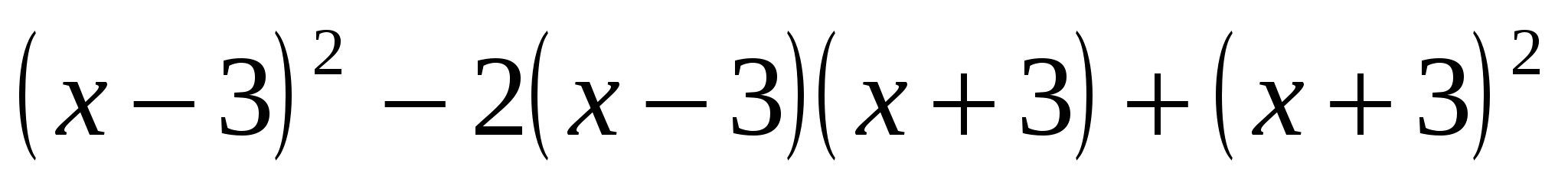 , при
, при 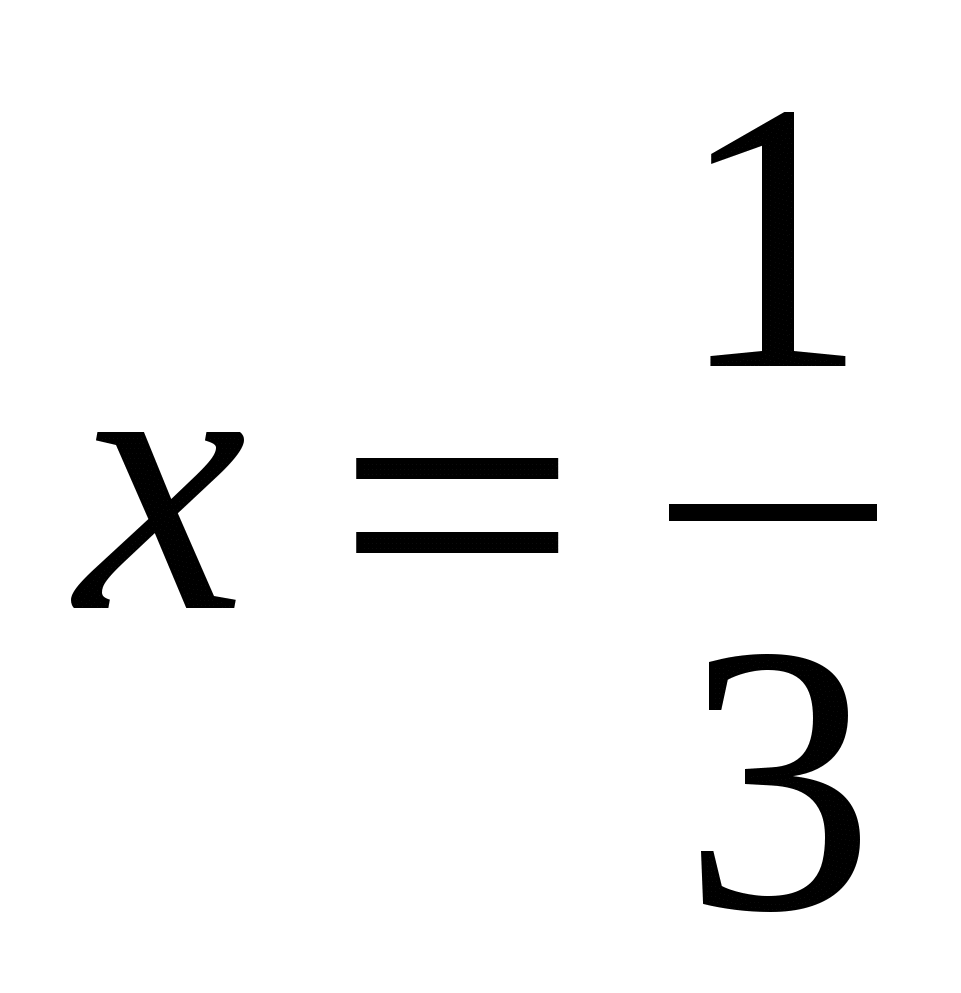 .
. -
Решите систему линейных уравнений методом Гаусса:
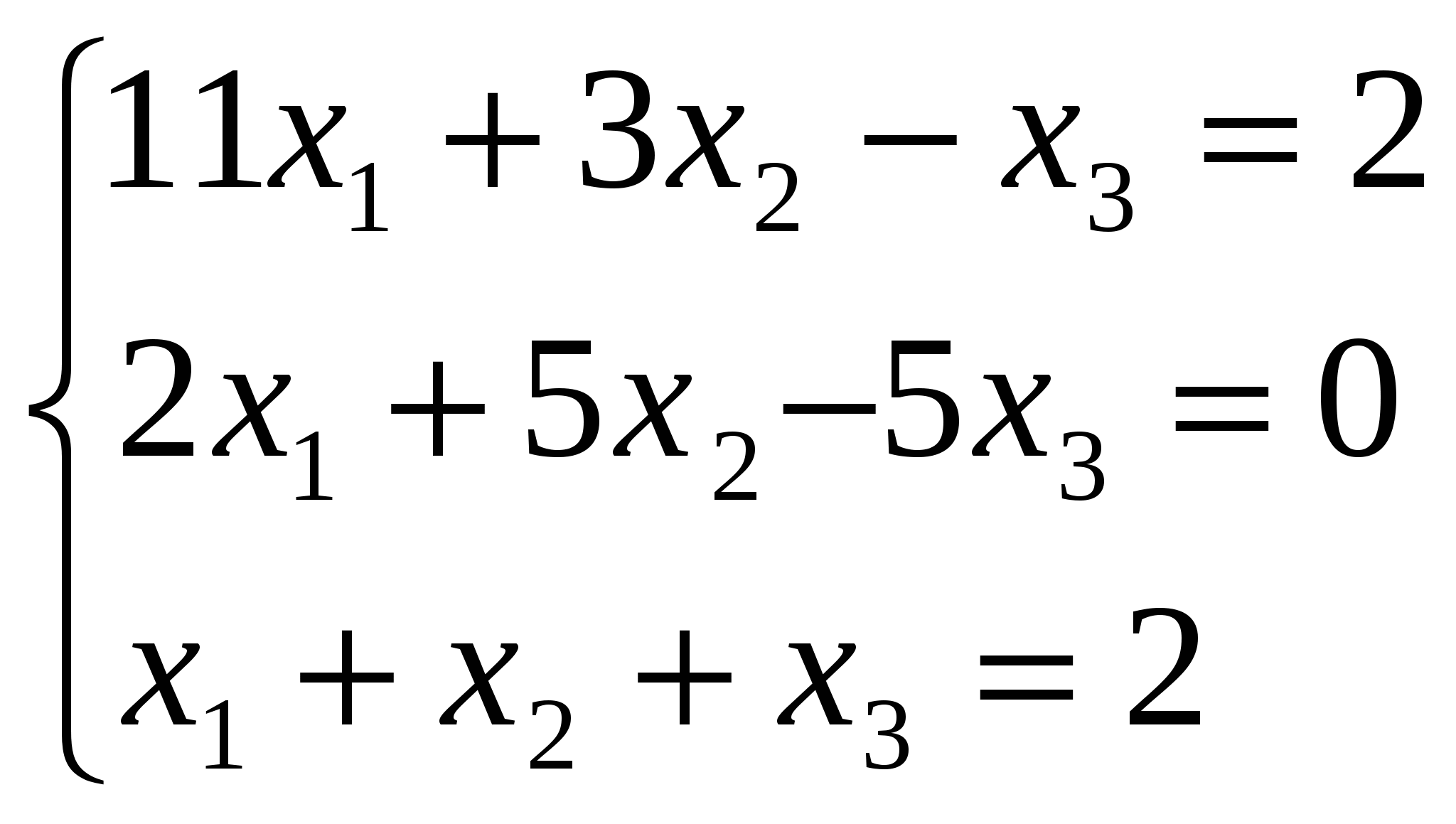
Вариант 3
При выполнении задания 1 – 11 в бланках ответа под номером соответствующего задания, поставьте номер правильного ответа.
-
Какое из указанных чисел является значением выражения
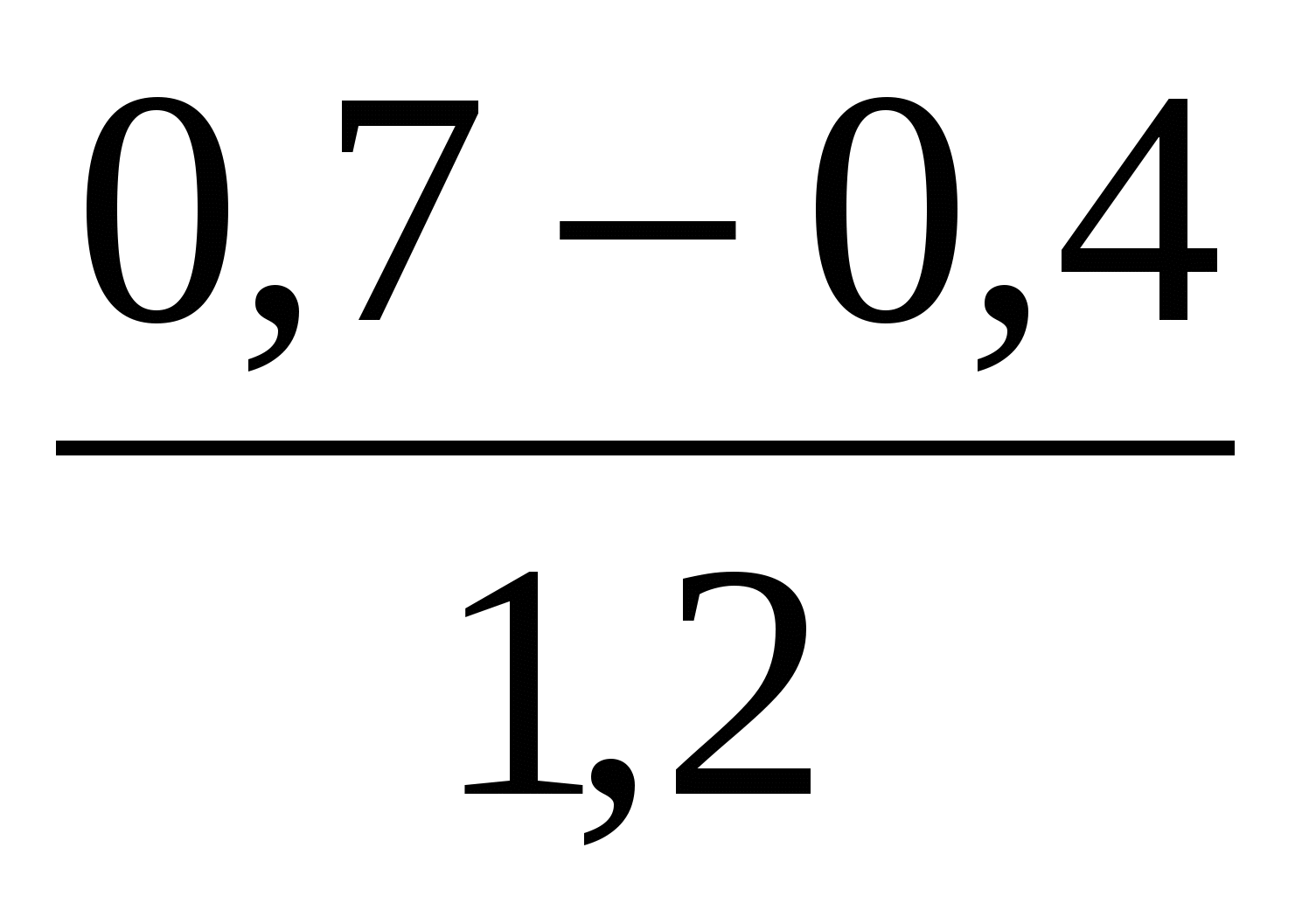 ?
?
1) 0,5 2) 0,25 3) 2,5 4) 5
-
Билет в театр стоит 150 рублей. Какое максимальное число билетов можно купить на 2000 рублей после повышения цены на 20%?
1) 10 2) 13 3) 11 4) 12
-
Найдите
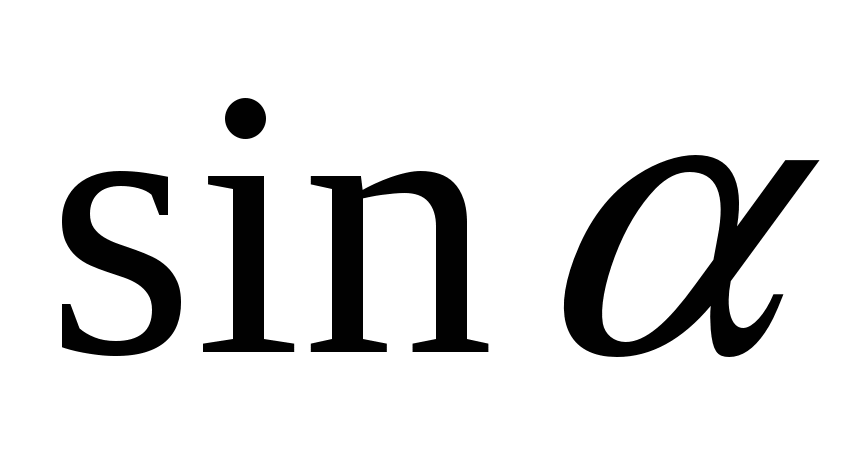 , если
, если 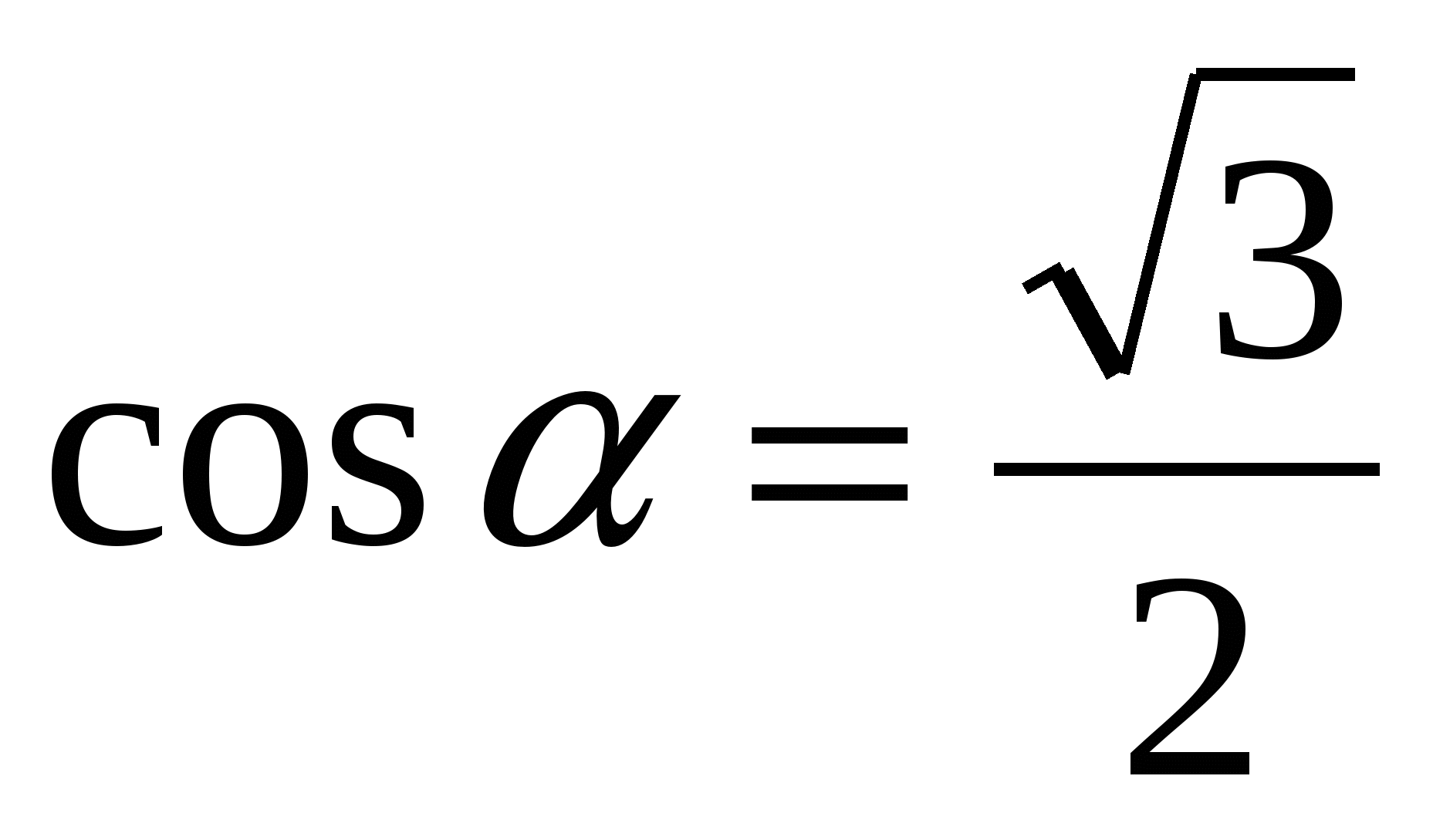 ,
, 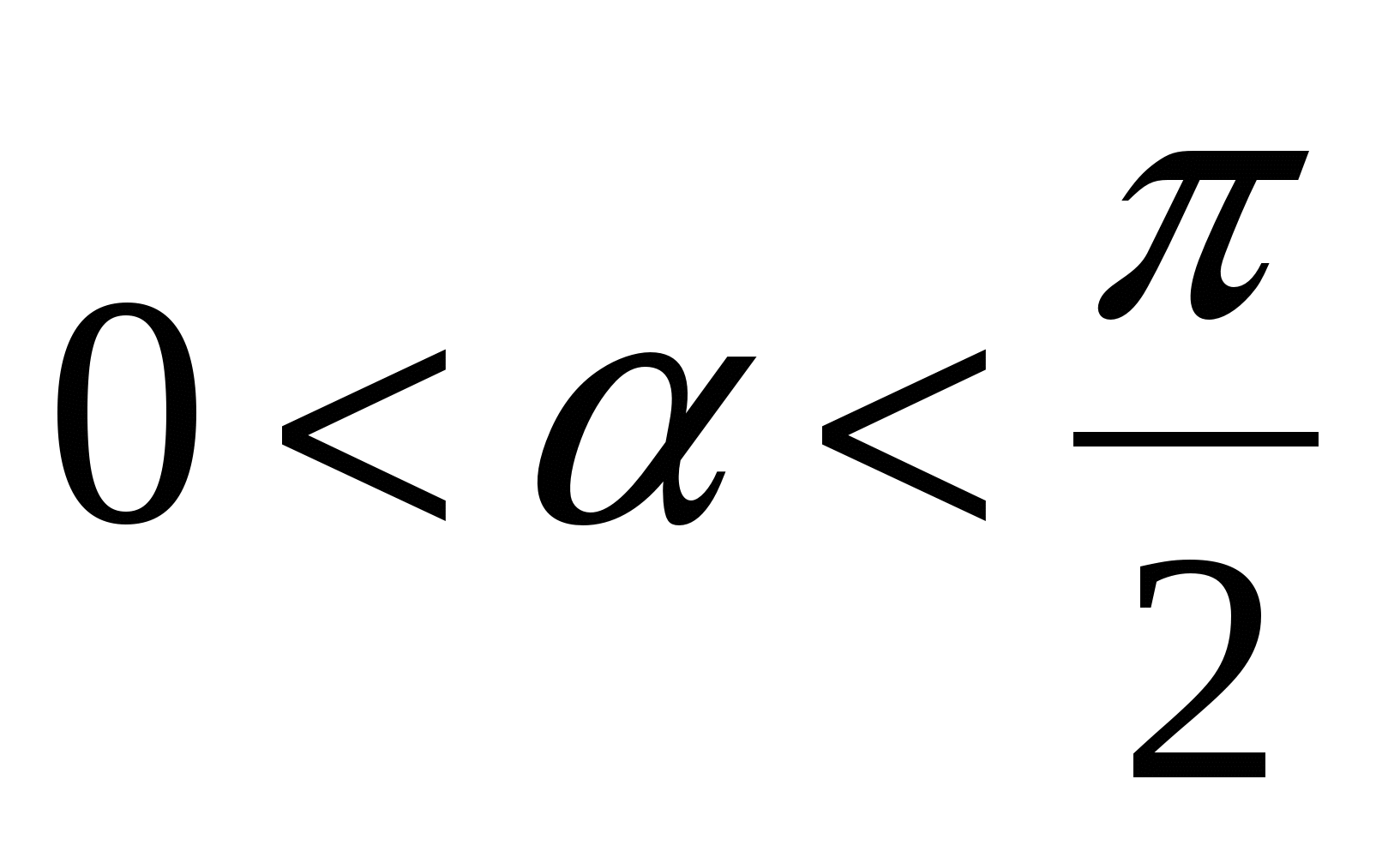 .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4) 1
4) 1
-
В сборнике по биологии всего 40 билетов, в восьми из них встречается вопрос о цветах. На экзамене школьнику достается один случайно выбранный билет из этого сборника. Какова вероятность того, что в этом билете будет вопрос о цветах?
1) 0,2 2) 0,8 3) 0,5 4) 5
-
Упростите выражение и выберите правильный ответ
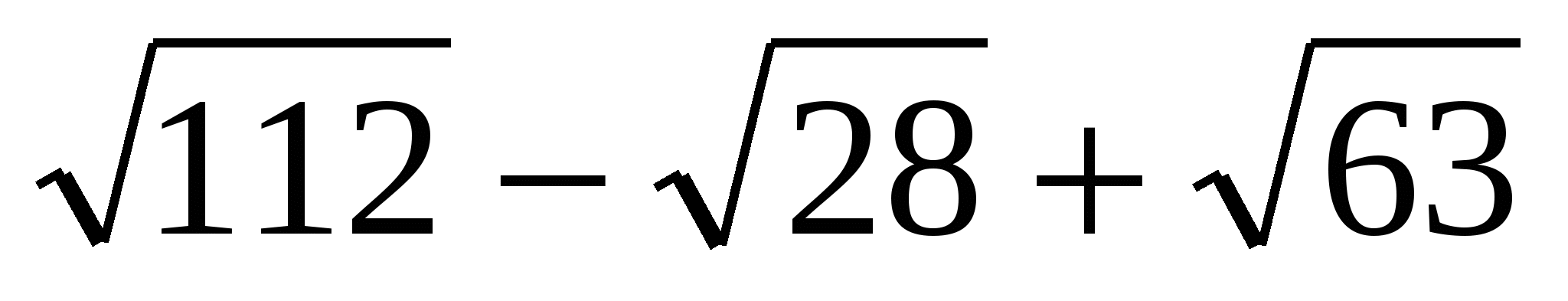 .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
-
Определите угловой коэффициент прямой
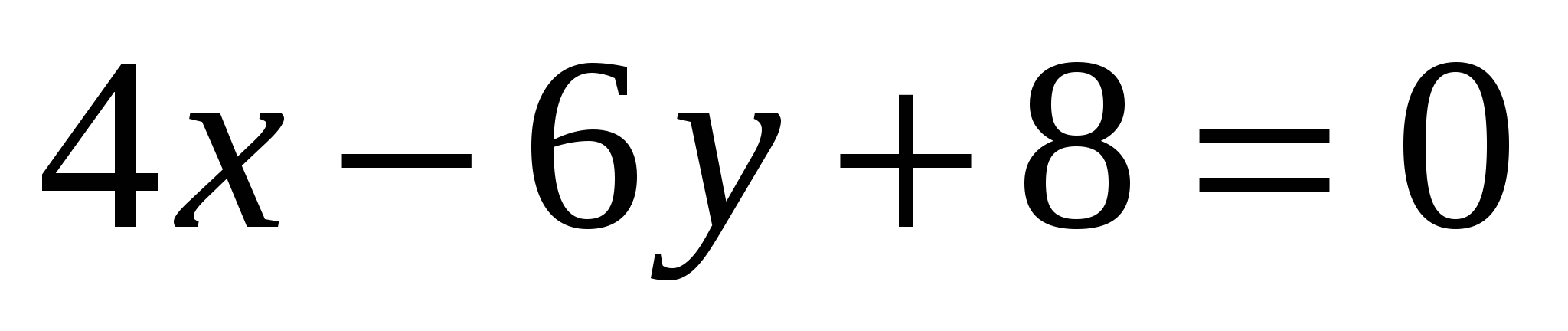 .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
-
Предел функции
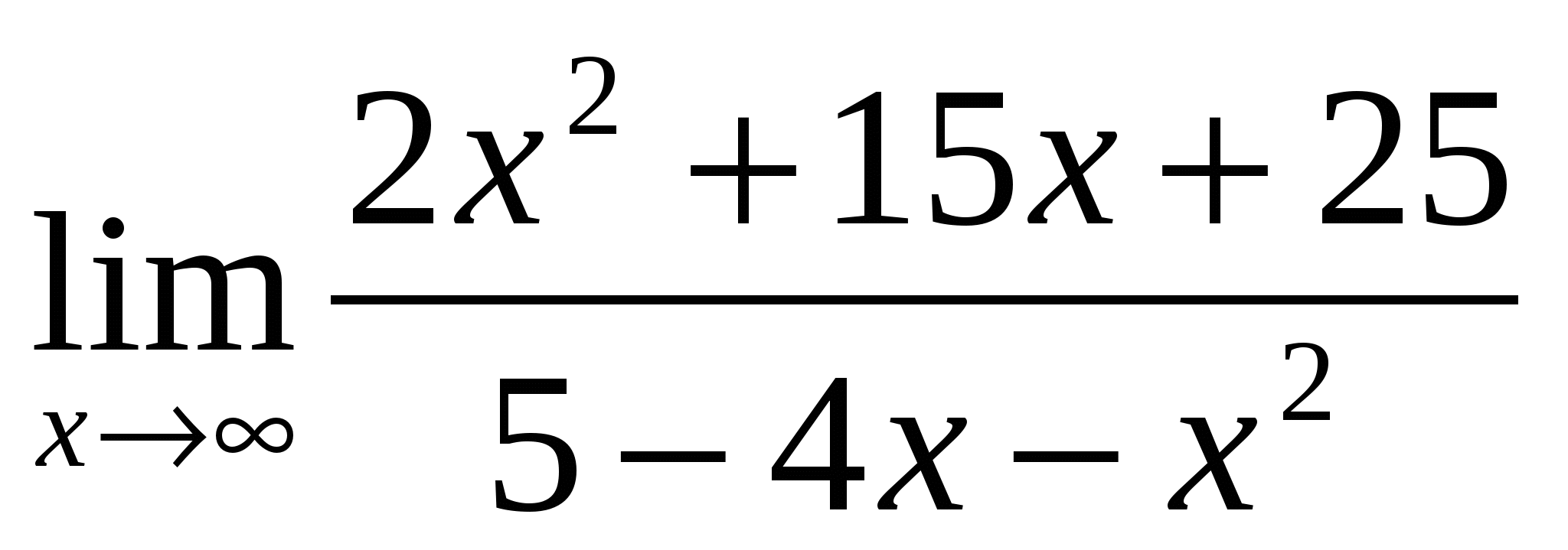 равен:
равен:
1) 5 2) – 2 3) ![]() 4)
4) ![]()
-
Объем первого цилиндра равен 9 см3. Найдите объем второго цилиндра, если при равных диаметрах, его высота в три раза меньше, чем у первого.
1) 27 2) 3 3) 1 4) 9
-
Площадь полной поверхности куба равна 150 см2. Найдите длину ребра.
1) 6 2) 37,5 3) 25 4) 5
-
Общее количество граней у икосаэдра равно
1) 20 2) 24 3) 30 4) 12
-
Число размещений 5 элементов по 3 равно
1) 120 2) 30 3) 60 4) 100
При выполнении задания 12 – 16 укажите сначала номер задания, а затем запишите его решение.
-
Вычислите значение производной заданной функции при указанном значении независимой переменной:
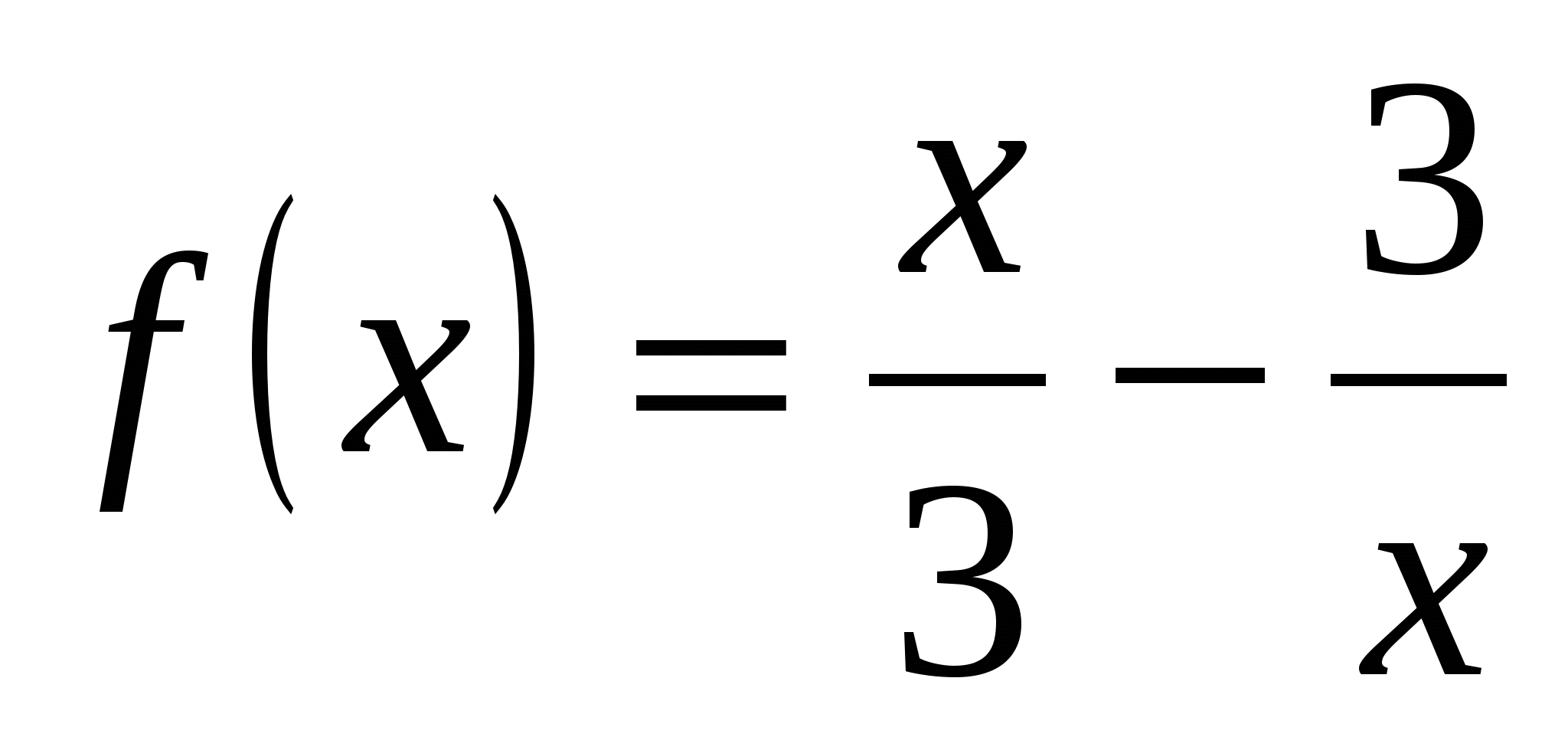 ;
; 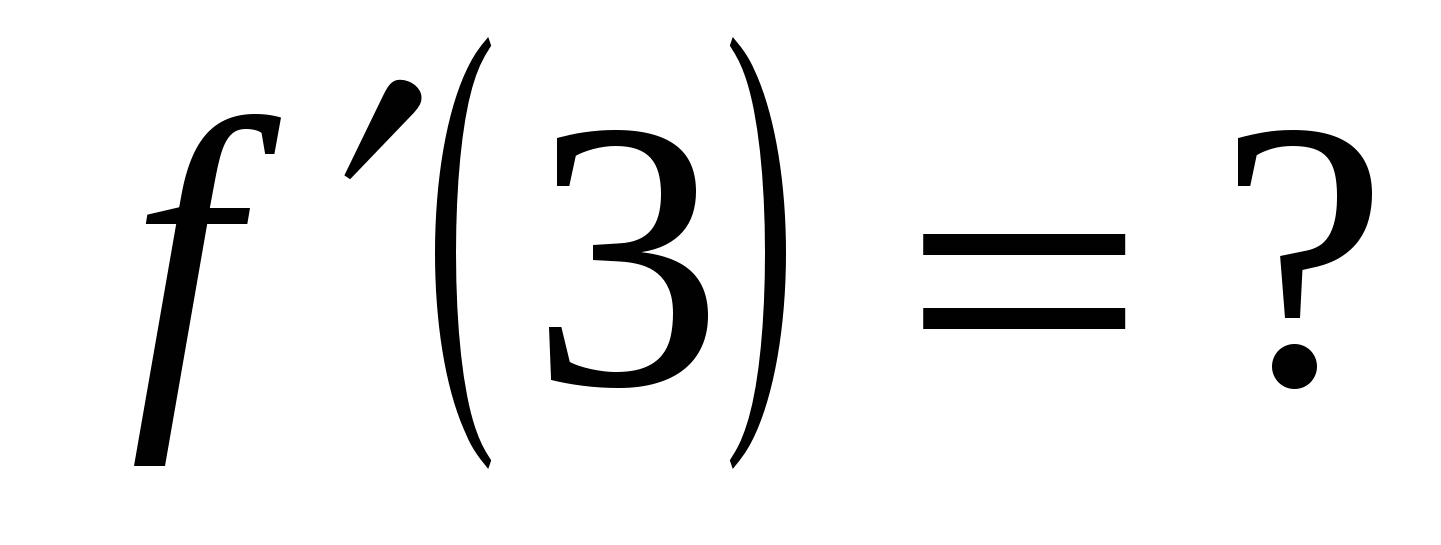
-
Найдите промежутки монотонности для функции
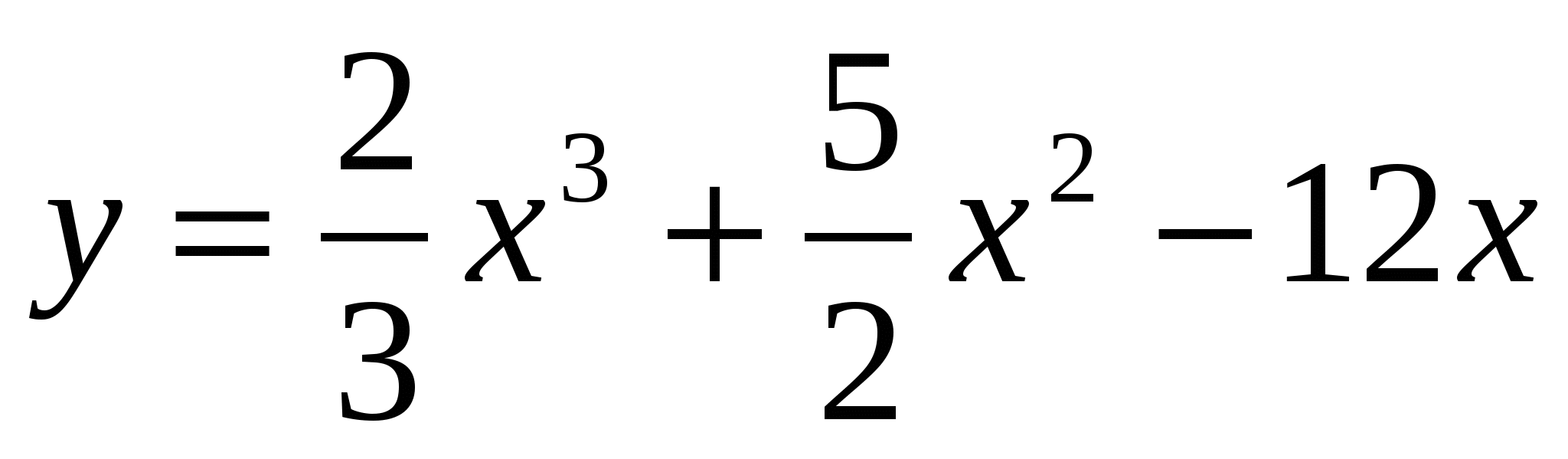 .
. -
Вычислите площадь фигуры, ограниченной заданными линиями
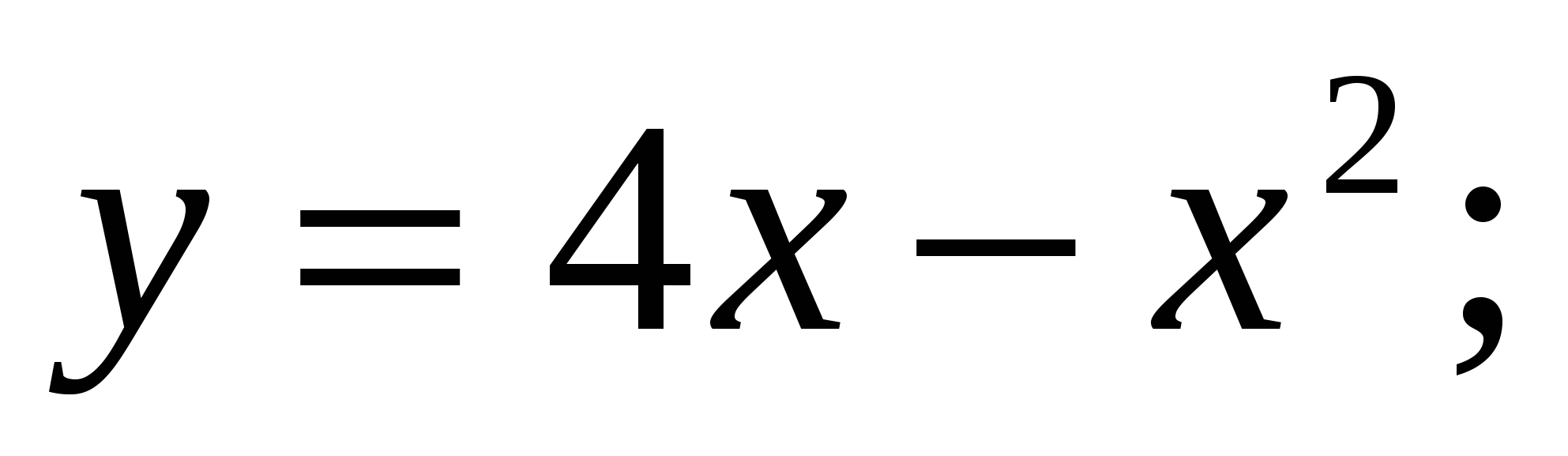
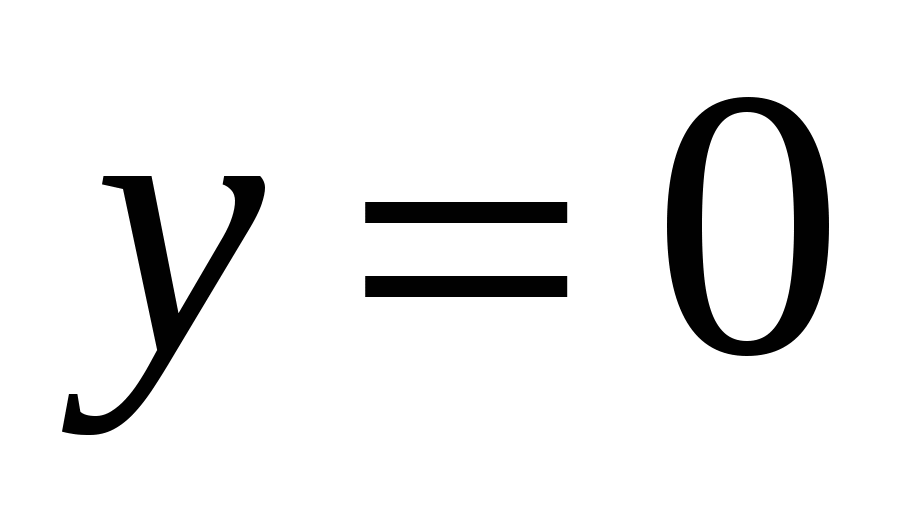 .
. -
Найдите значение выражения
 , при
, при 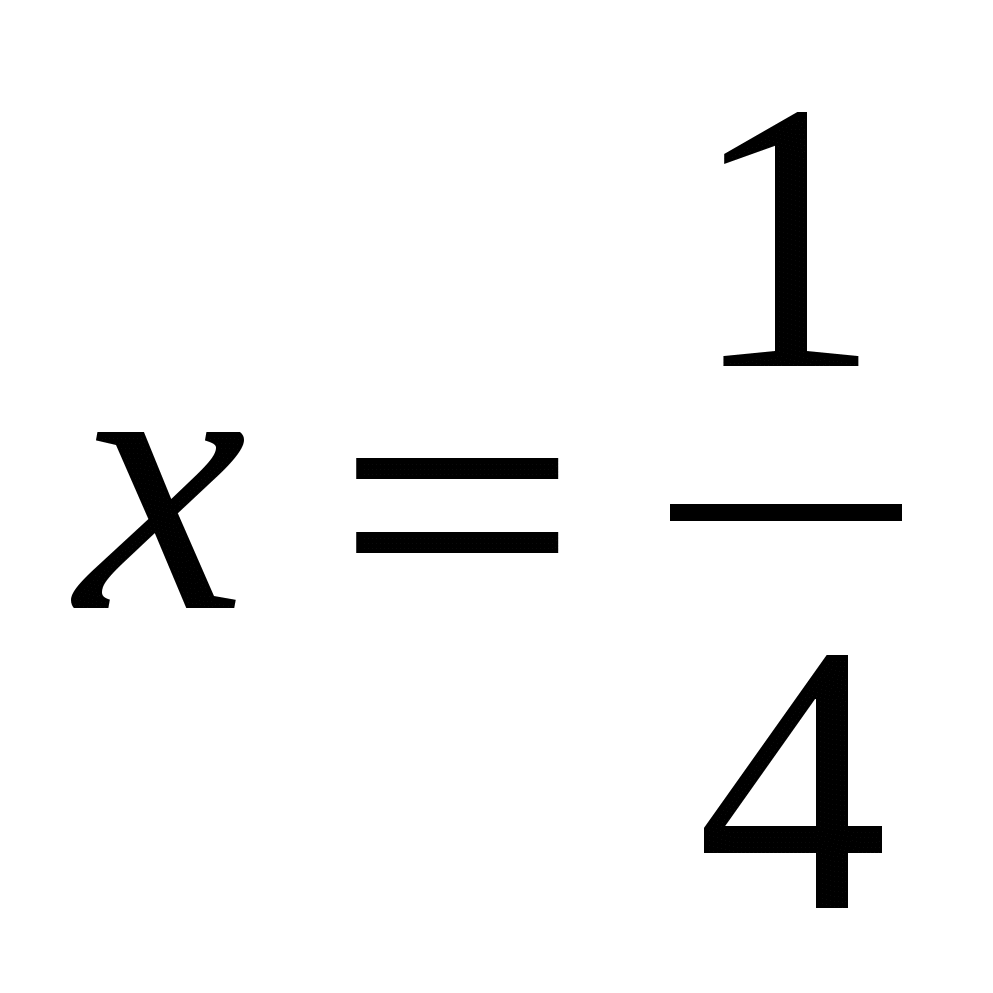 .
. -
Решите систему линейных уравнений методом Гаусса:
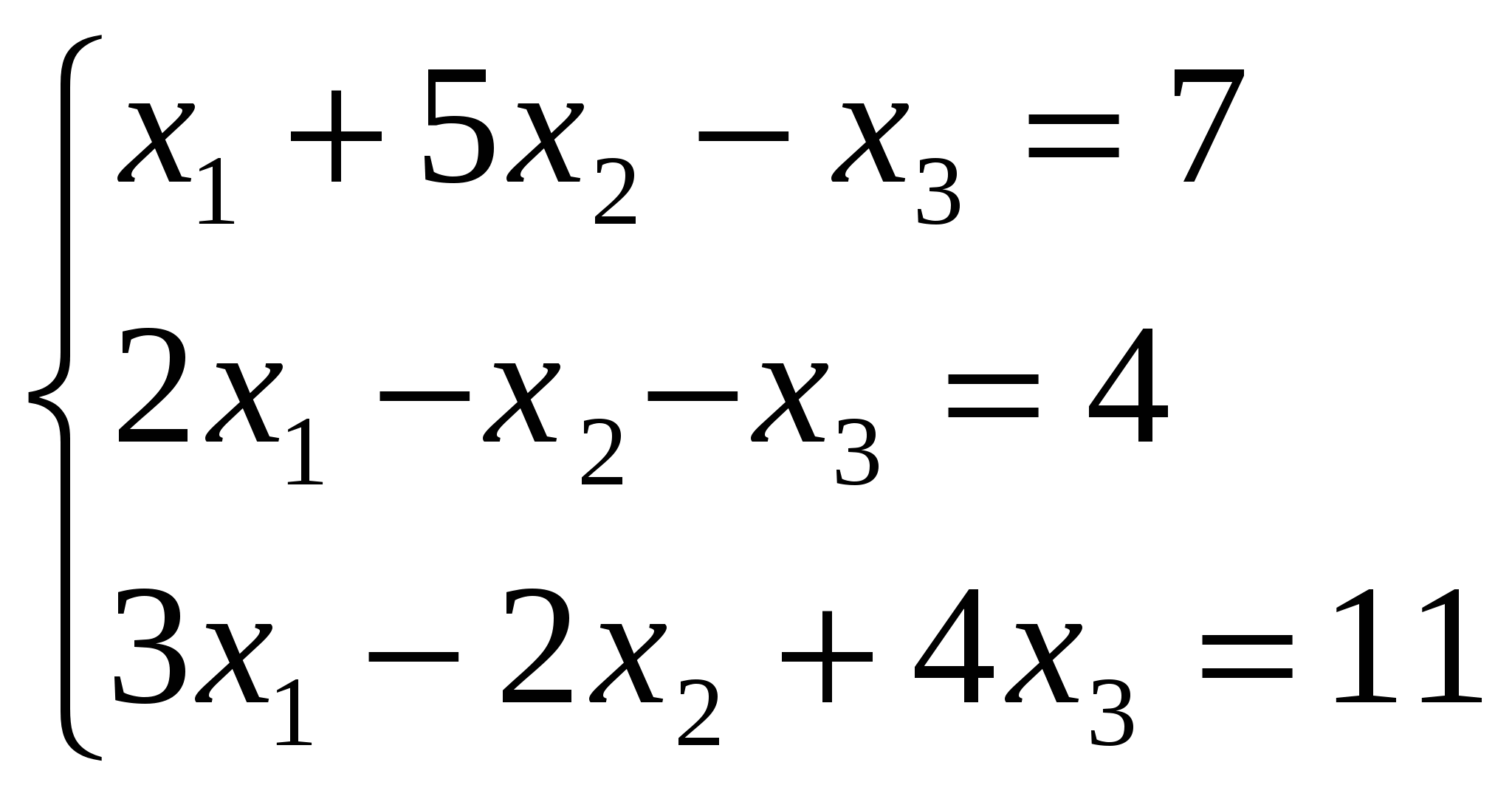
Вариант 4
При выполнении задания 1 – 11 в бланках ответа под номером соответствующего задания, поставьте номер правильного ответа.
-
Какое из указанных чисел является значением выражения
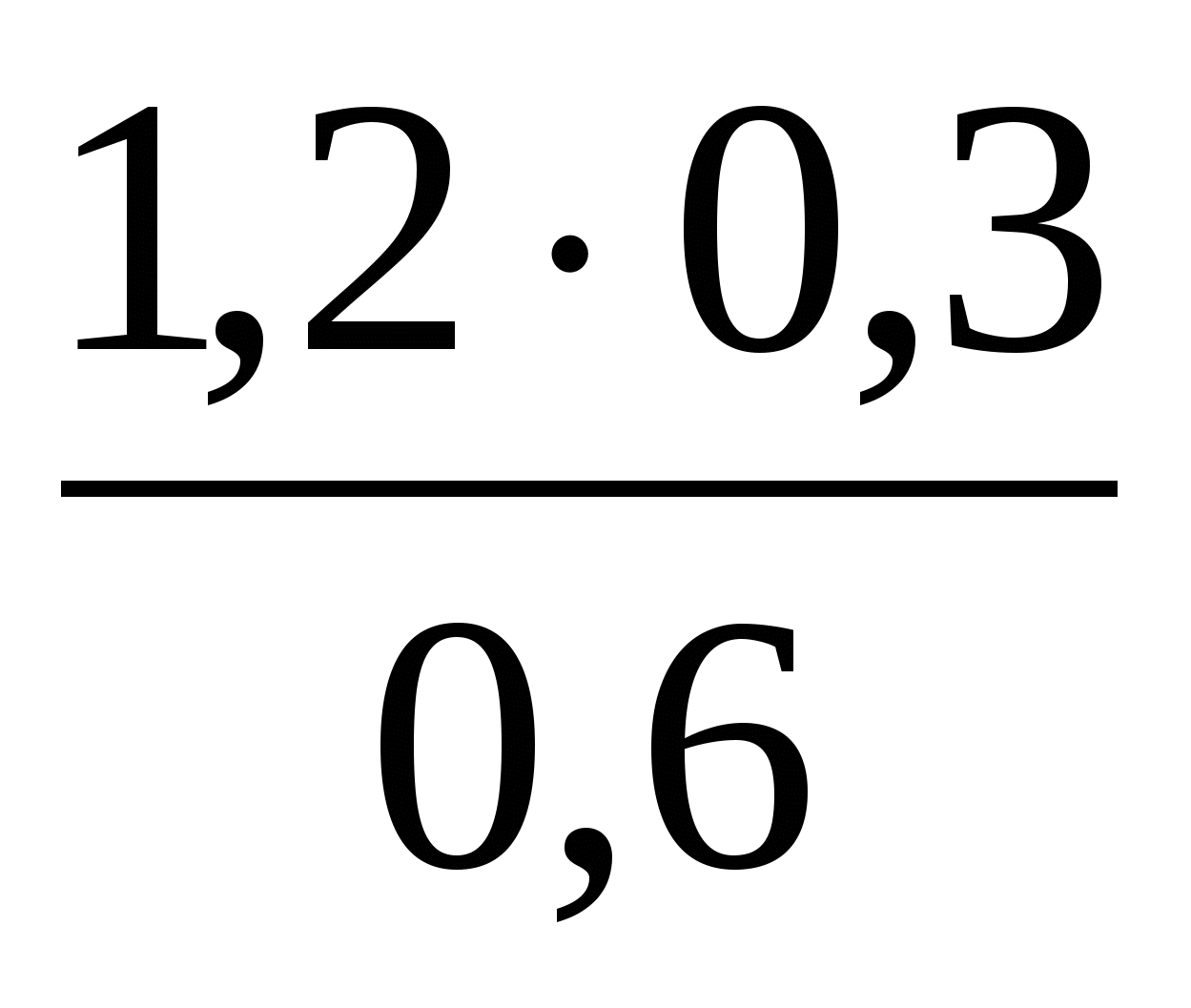 ?
?
1) 2 2) 0,6 3) 0,5 4) 6
-
Билет на автобус стоит 14 рублей. Какое максимальное число билетов можно купить на 100 рублей после повышения цены на 5%?
1) 4 2) 6 3) 5 4) 7
-
Найдите
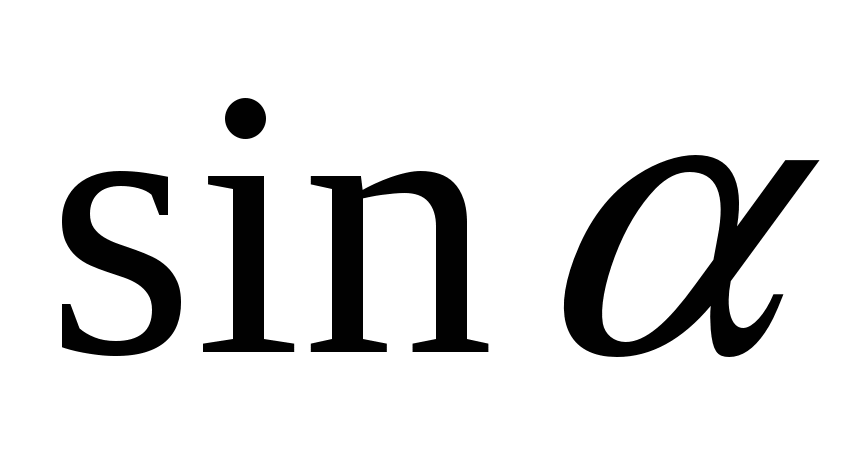 , если
, если 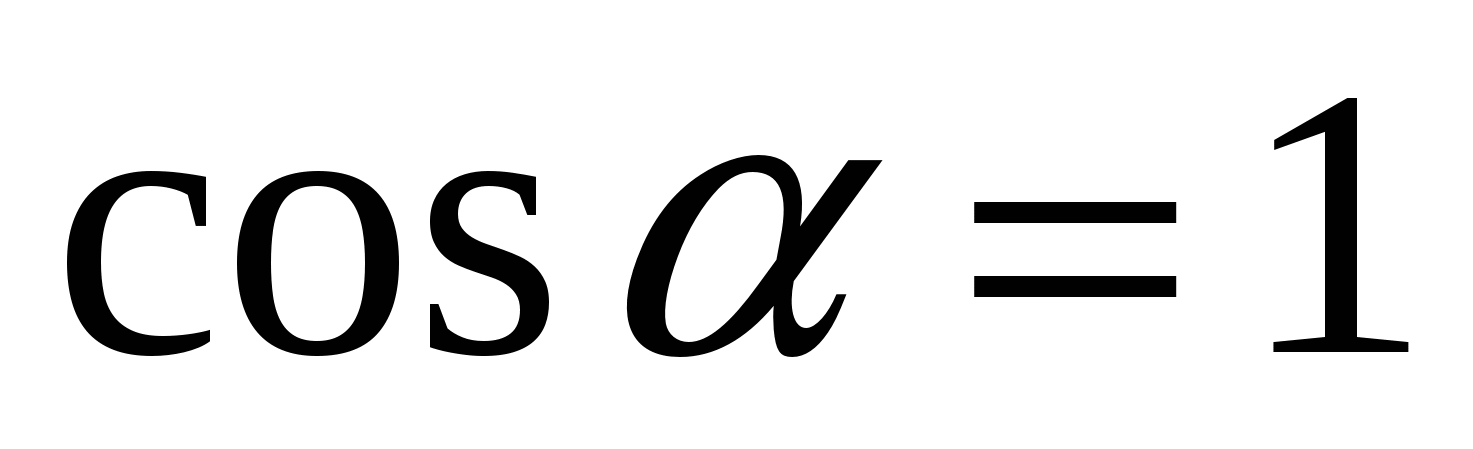 ,
, 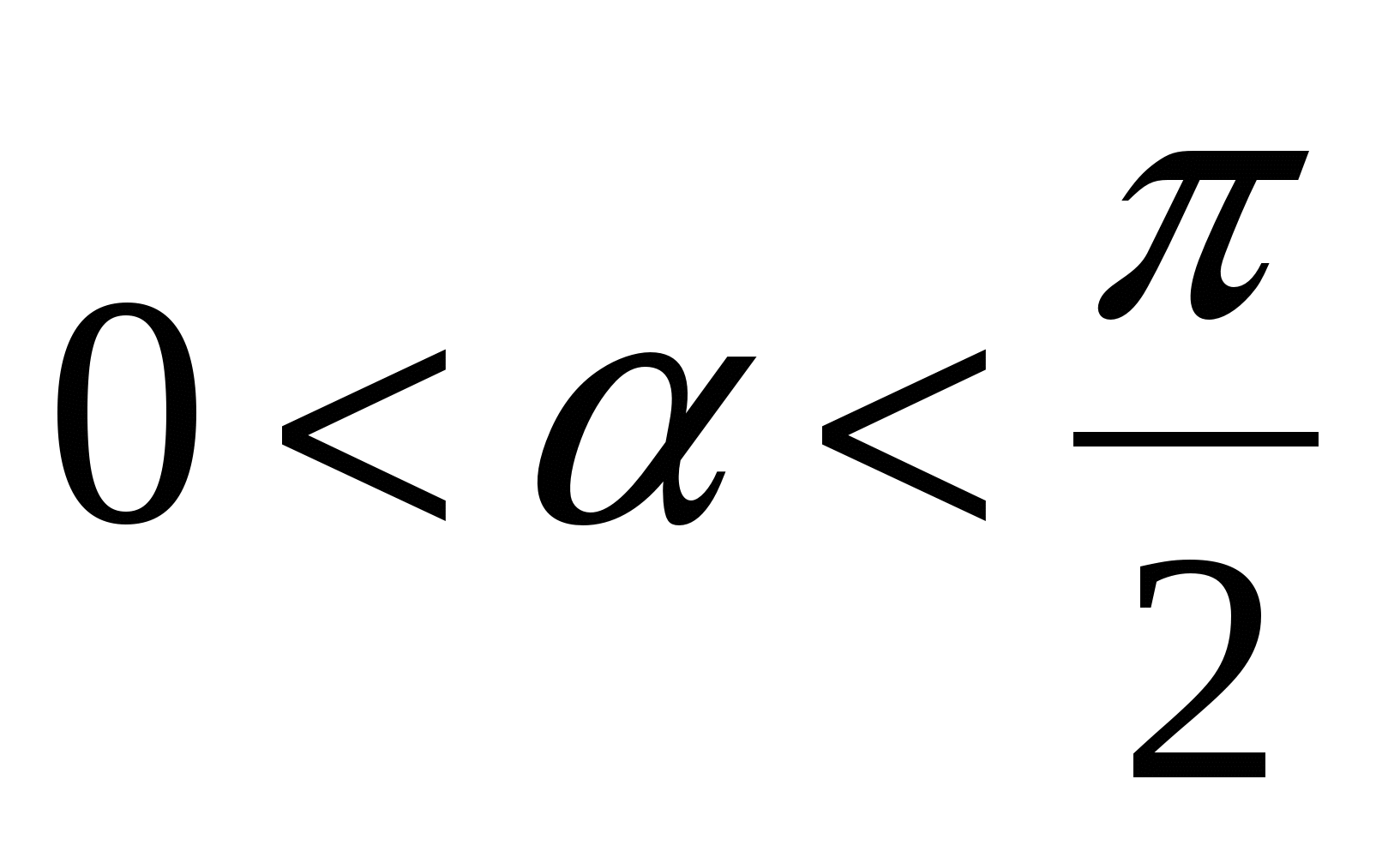 .
.
1) ![]() 2) 0 3)
2) 0 3) ![]() 4) 1
4) 1
-
В сборнике по географии всего 35 билетов, в семи из них встречается вопрос о материках. На экзамене школьнику достается один случайно выбранный билет из этого сборника. Какова вероятность того, что в этом билете будет вопрос о материках?
1) 0,2 2) 0,8 3) 0,5 4) 5
-
Упростите выражение и выберите правильный ответ
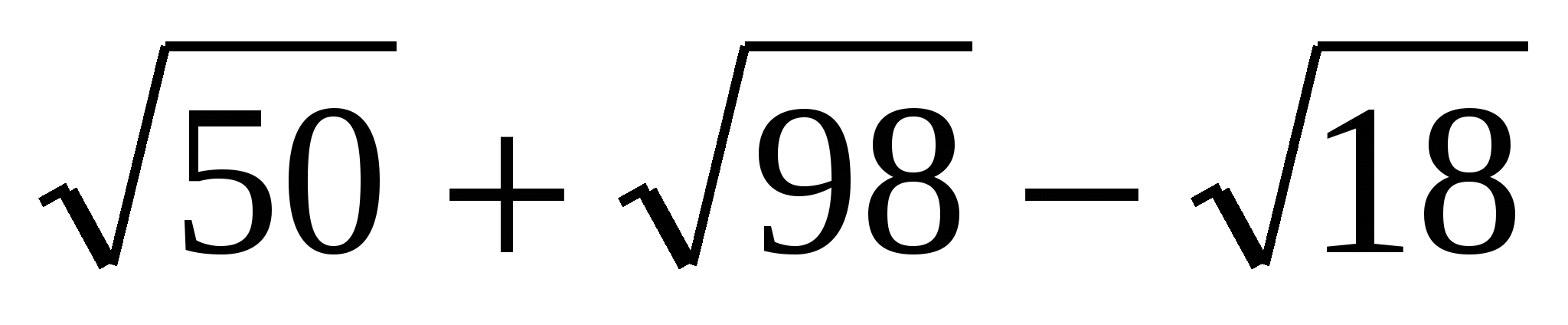 .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
-
Определите угловой коэффициент прямой
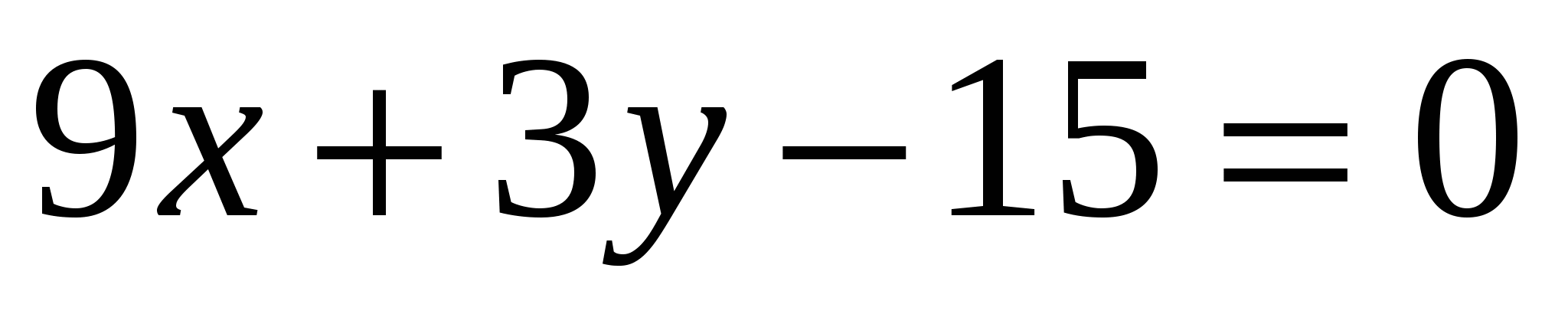 .
.
1) – 3 2) ![]() 3) 3 4)
3) 3 4)![]()
-
Предел функции
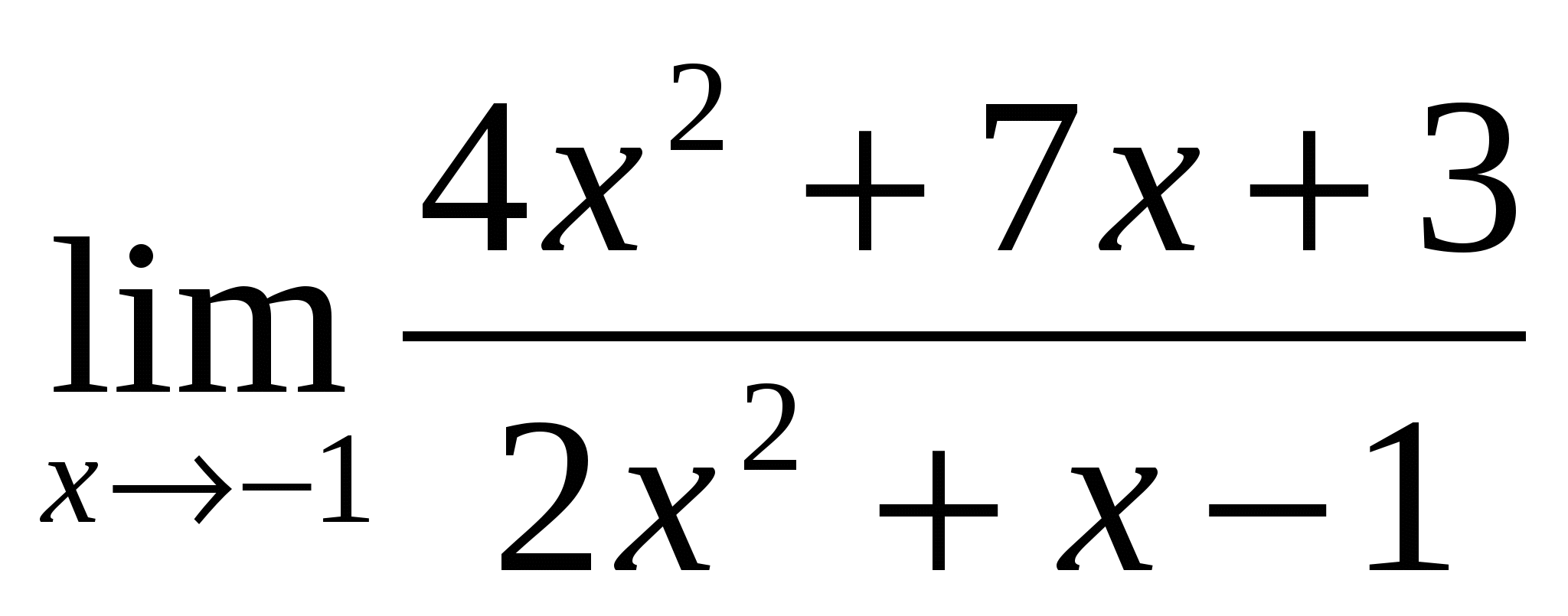 равен:
равен:
1) 2 2) 0 3) ![]() 4)
4) ![]()
-
Объем первого цилиндра равен 10 см3. Найдите объем второго цилиндра, если при равных высотах, его диаметр в два раза больше, чем у первого.
1) 2,5 2) 5 3) 40 4) 20
-
Площадь полной поверхности куба равна 24 см2. Найдите длину ребра.
1) 6 2) 8 3) 4 4) 2
-
Общее количество вершин у октаэдра равно
1) 4 2) 6 3) 10 4) 8
-
Число размещений 5 элементов по 2 равно
1) 20 2) 30 3) 10 4) 50
При выполнении задания 12 – 16 укажите сначала номер задания, а затем запишите его решение.
-
Вычислите значение производной заданной функции при указанном значении независимой переменной:
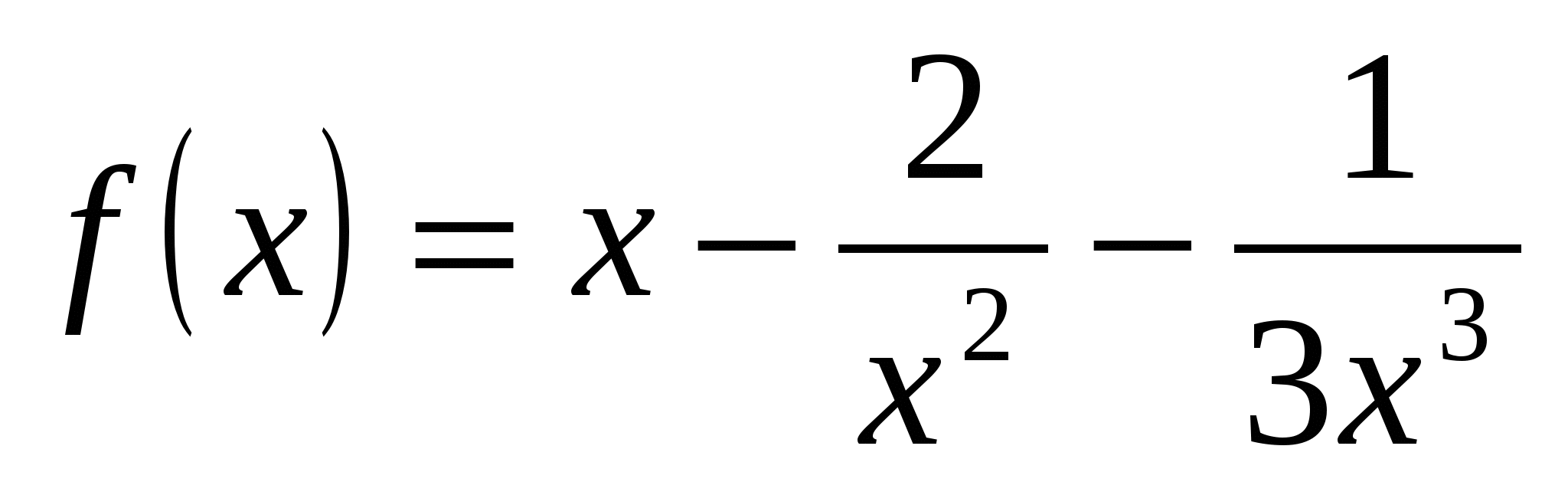 ;
; 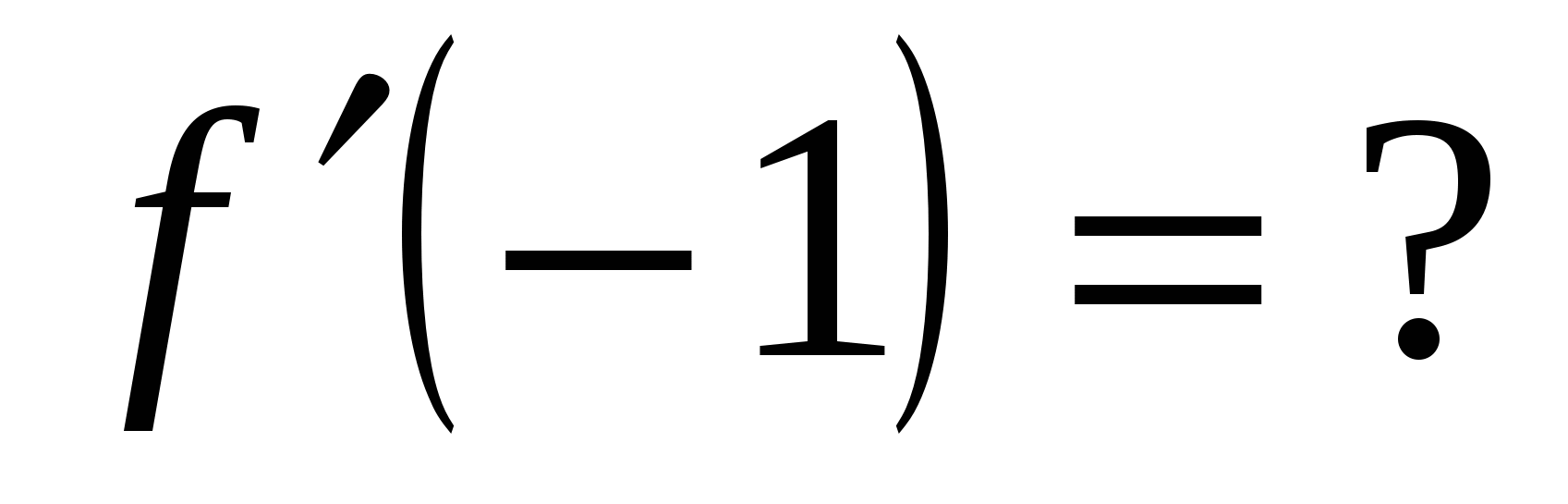
-
Найдите промежутки монотонности для функции
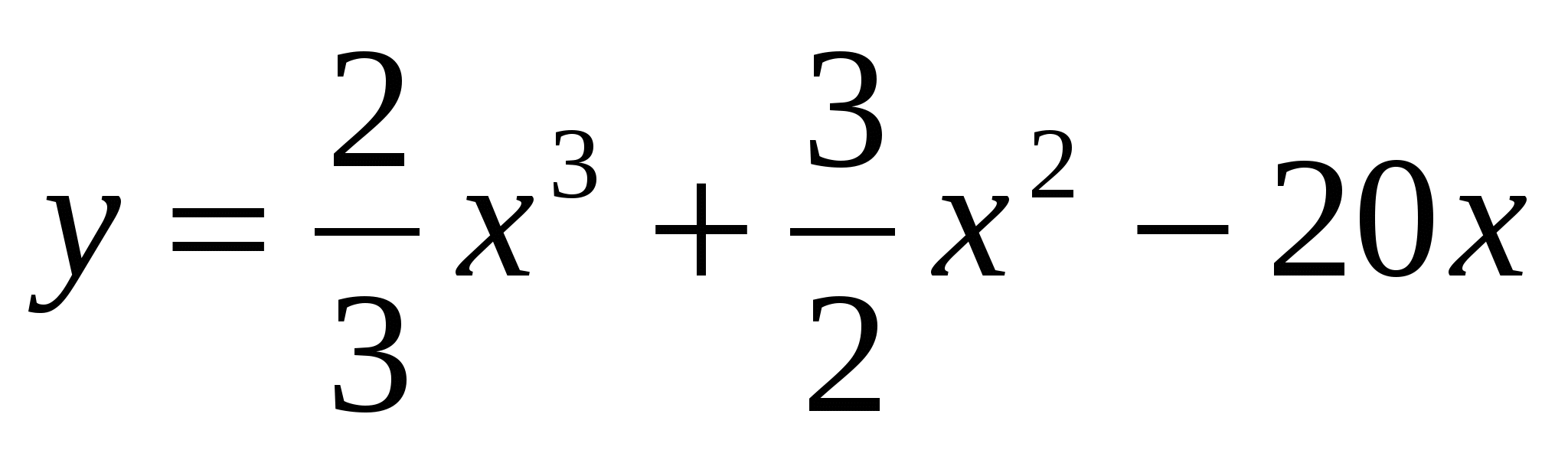 .
. -
Вычислите площадь фигуры, ограниченной заданными линиями
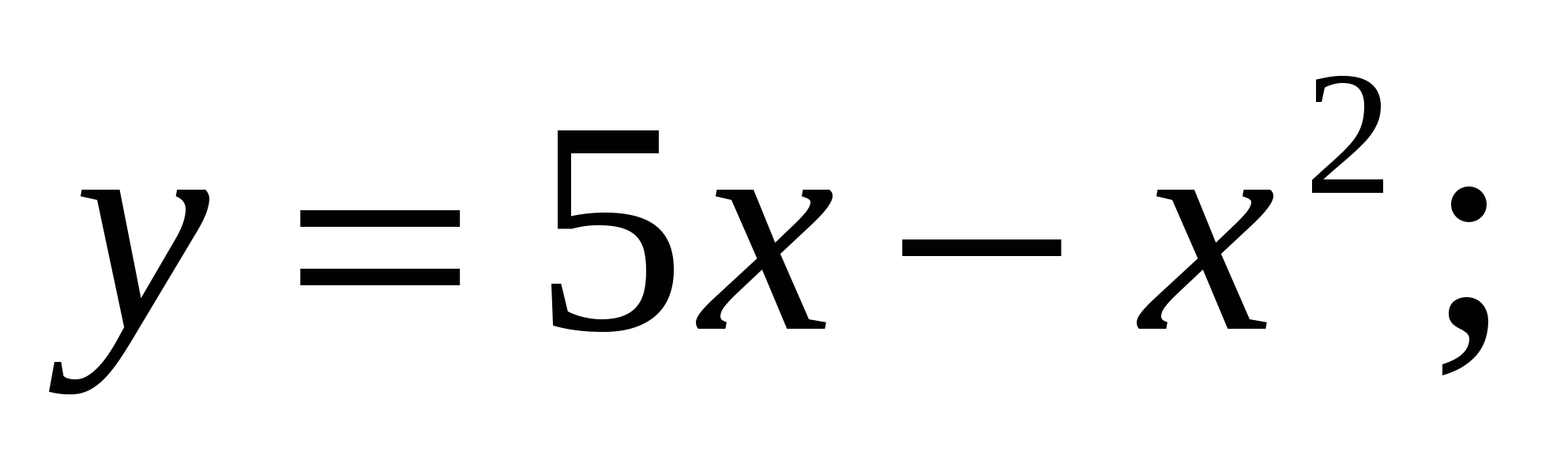
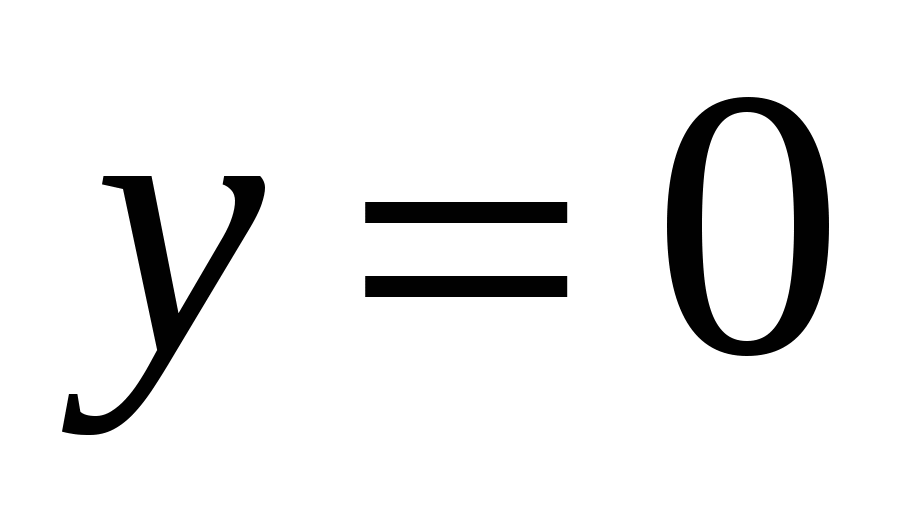 .
. -
Найдите значение выражения
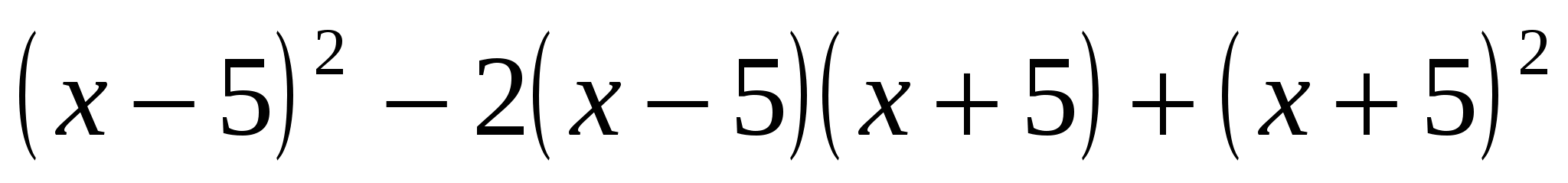 , при
, при 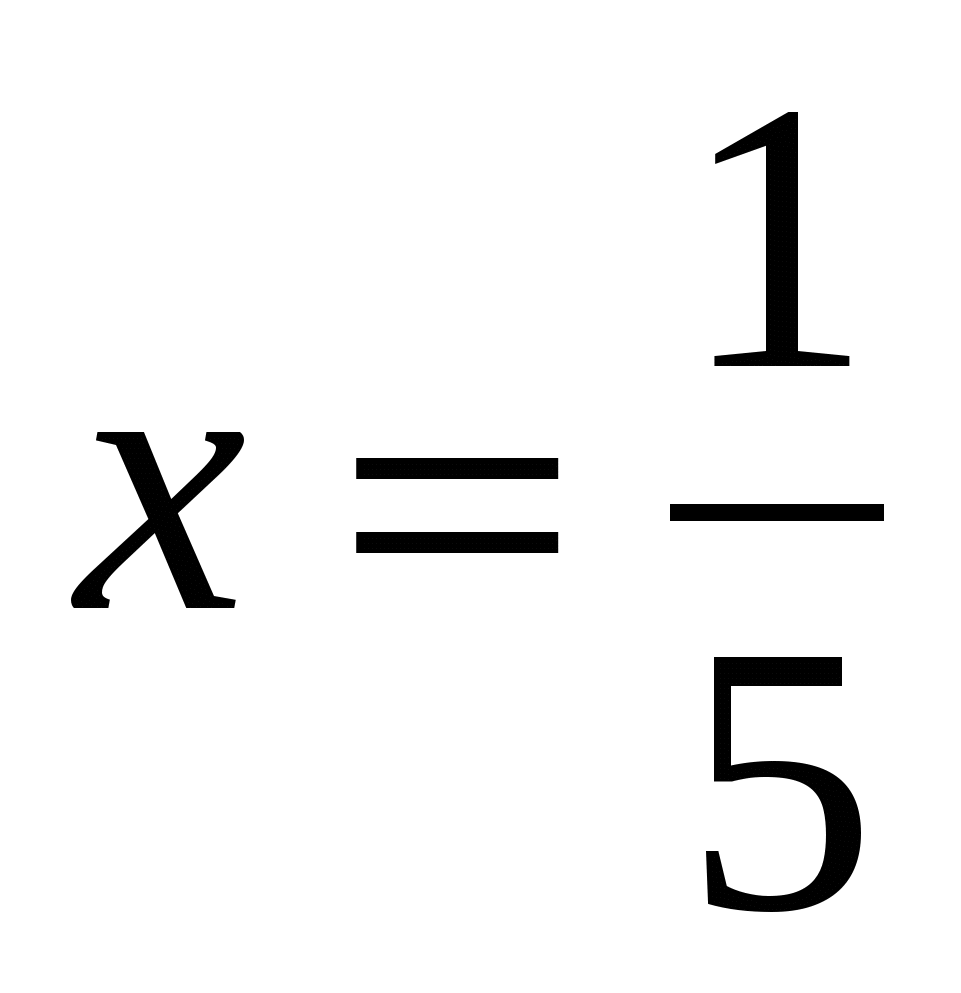 .
. -
Решите систему линейных уравнений методом Гаусса:
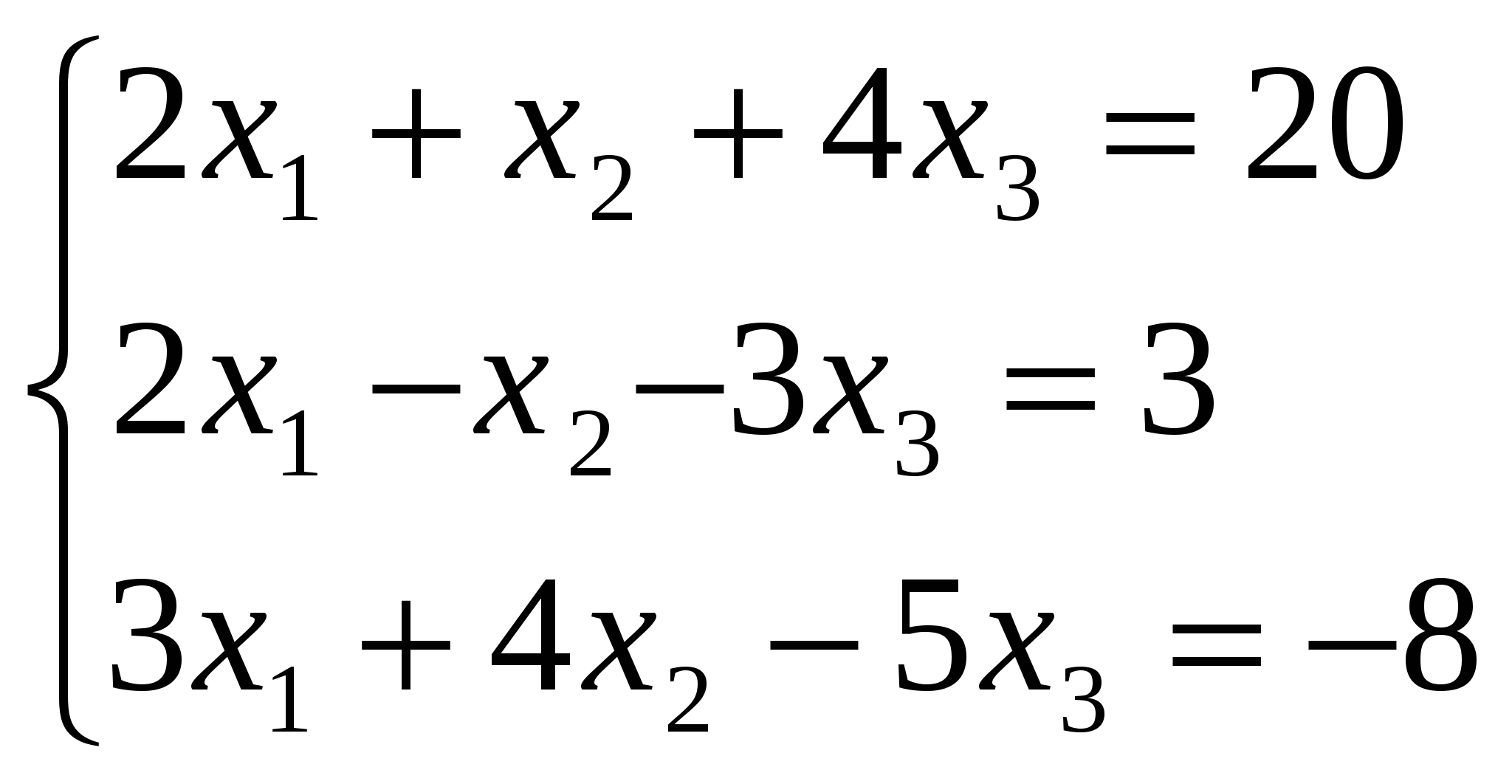
Вариант 5
При выполнении задания 1 – 11 в бланках ответа под номером соответствующего задания, поставьте номер правильного ответа.
-
Какое из указанных чисел является значением выражения
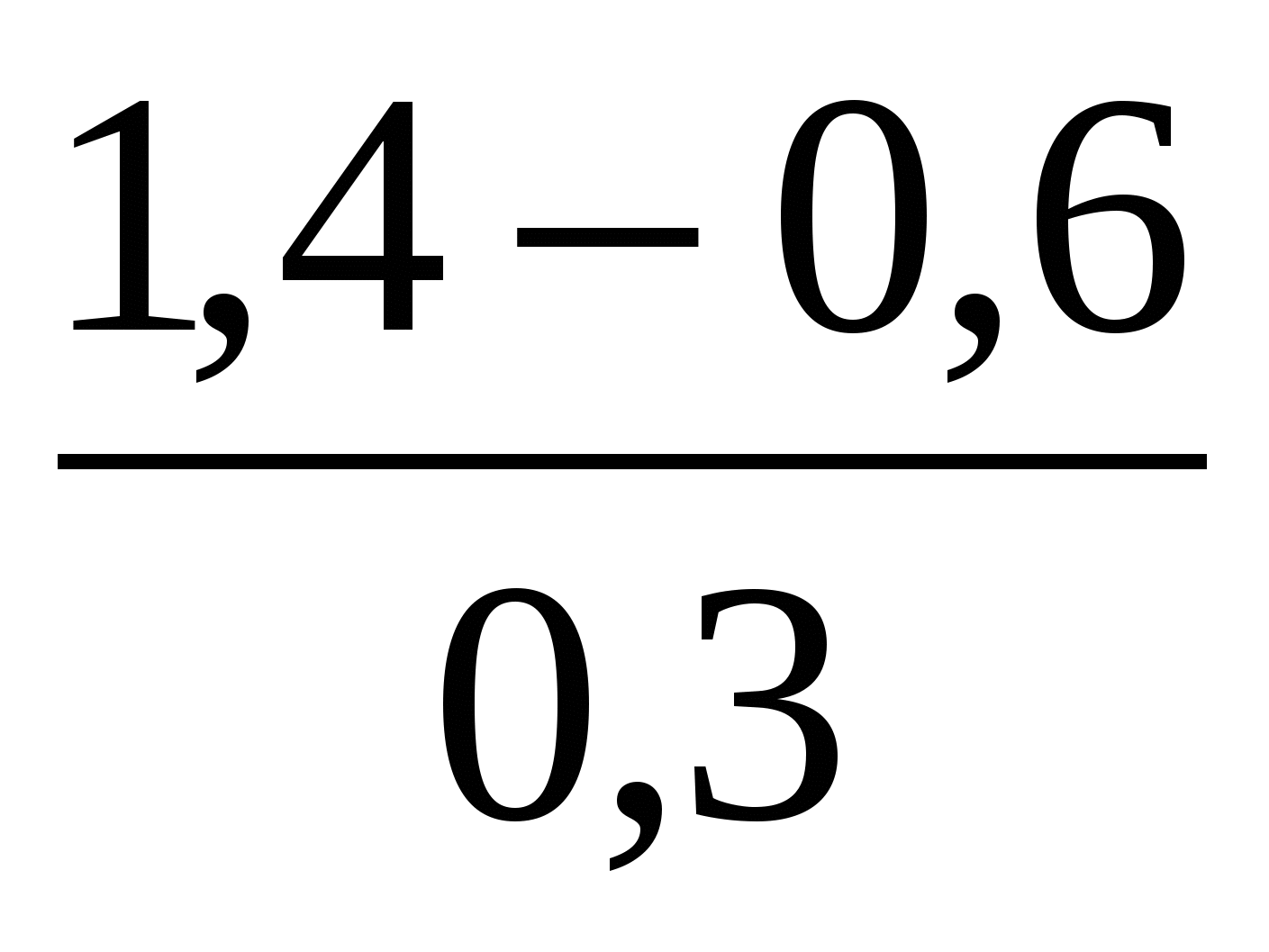 ?
?
1) ![]() 2) 4,2 3)
2) 4,2 3) ![]() 4) 2,6
4) 2,6
-
Билет в кино стоит 400 рублей. Какое максимальное число билетов можно купить на 4000 рублей после повышения цены на 20%?
1) 7 2) 8 3) 9 4) 10
-
Найдите
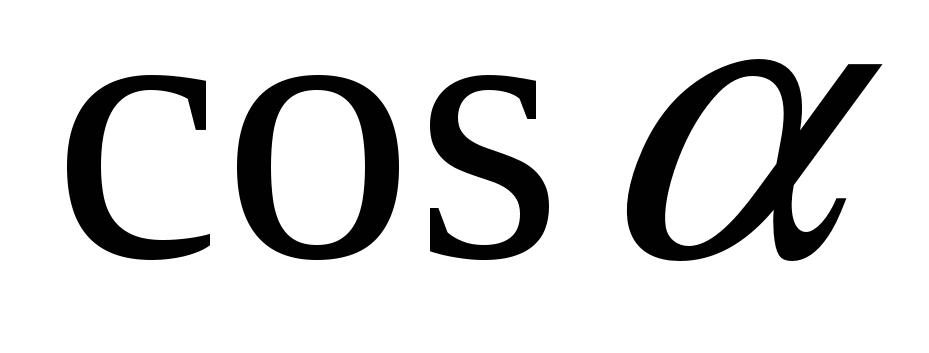 , если
, если 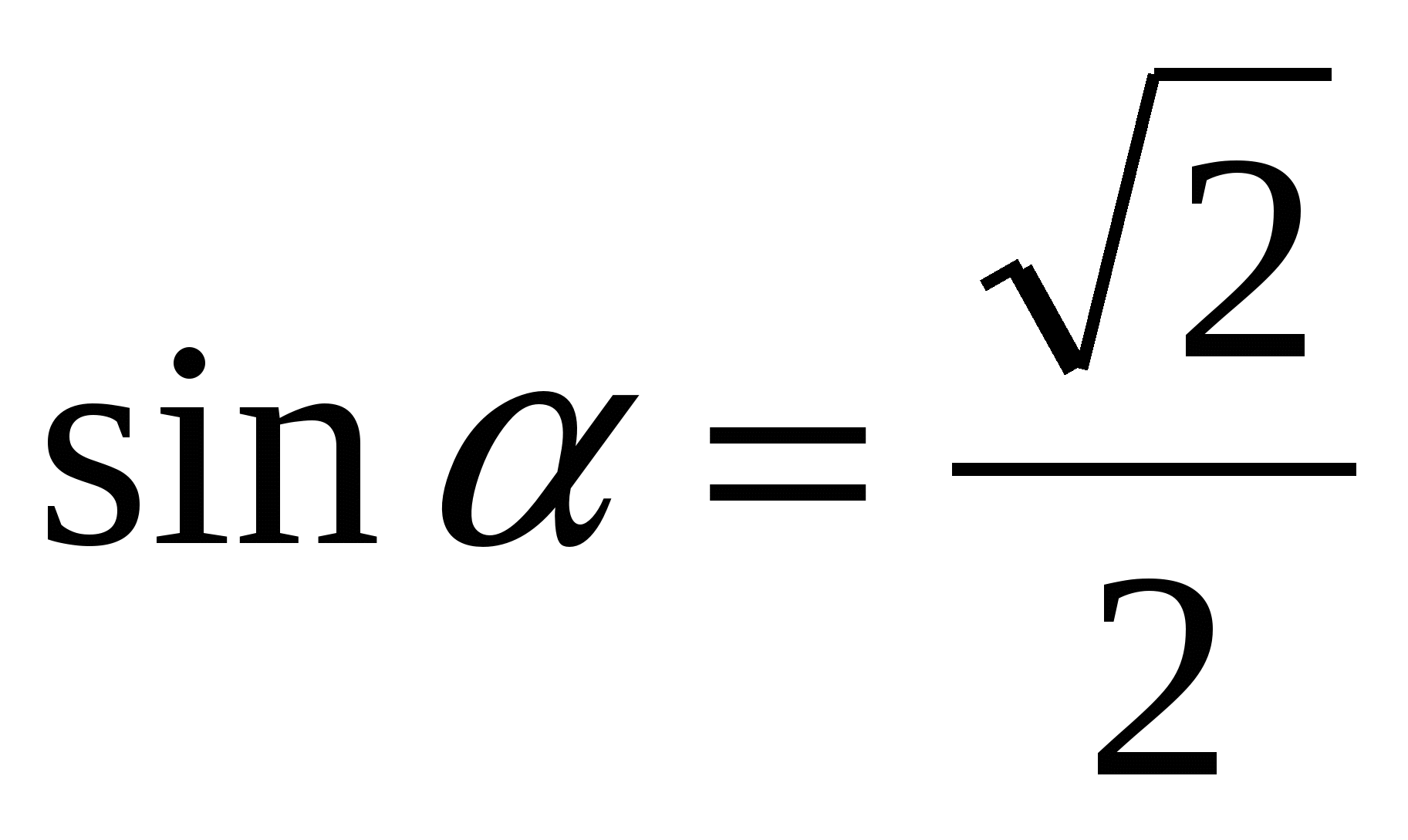 ,
, 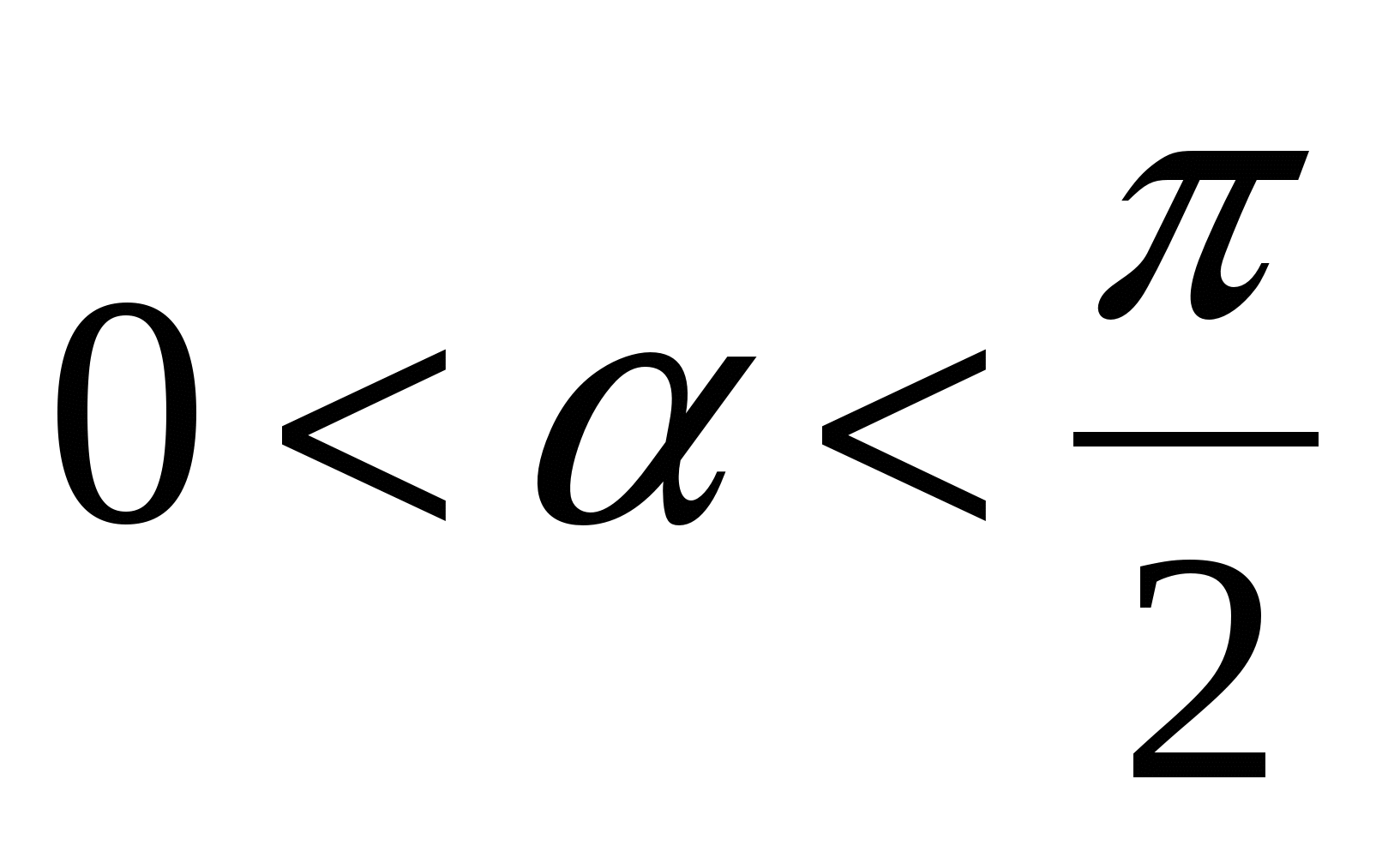 .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4) 1
4) 1
-
В сборнике по географии всего 32 билета, в восьми из них встречается вопрос о морях. На экзамене школьнику достается один случайно выбранный билет из этого сборника. Какова вероятность того, что в этом билете не будет вопроса о морях?
1) 0,25 2) 0,85 3) 0,55 4) 0,75
-
Упростите выражение и выберите правильный ответ
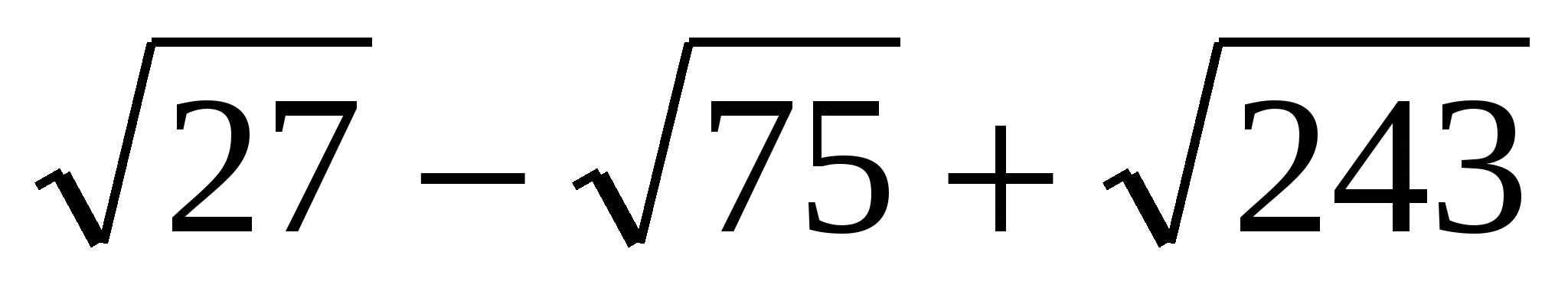 .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
-
Определите угловой коэффициент прямой
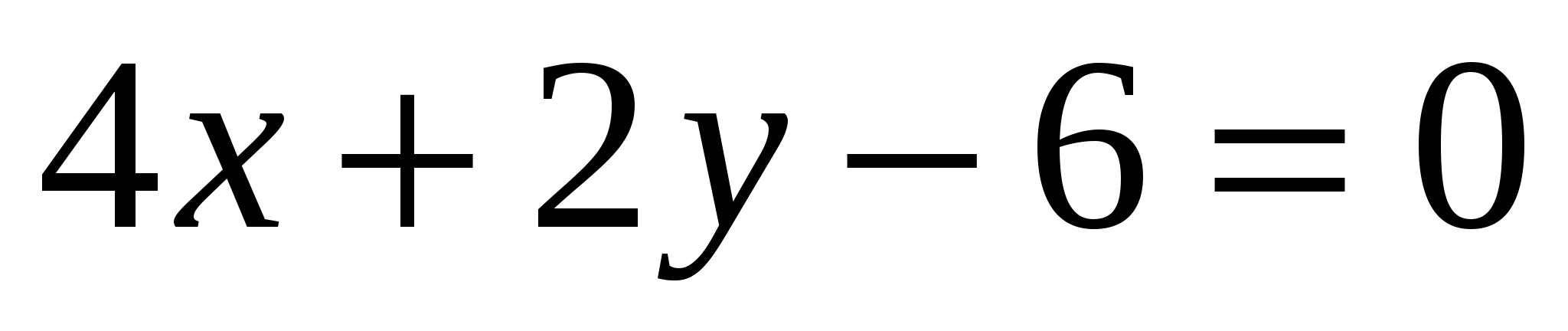 .
.
1) – 2 2) ![]() 3) 2 4)
3) 2 4)![]()
-
Предел функции
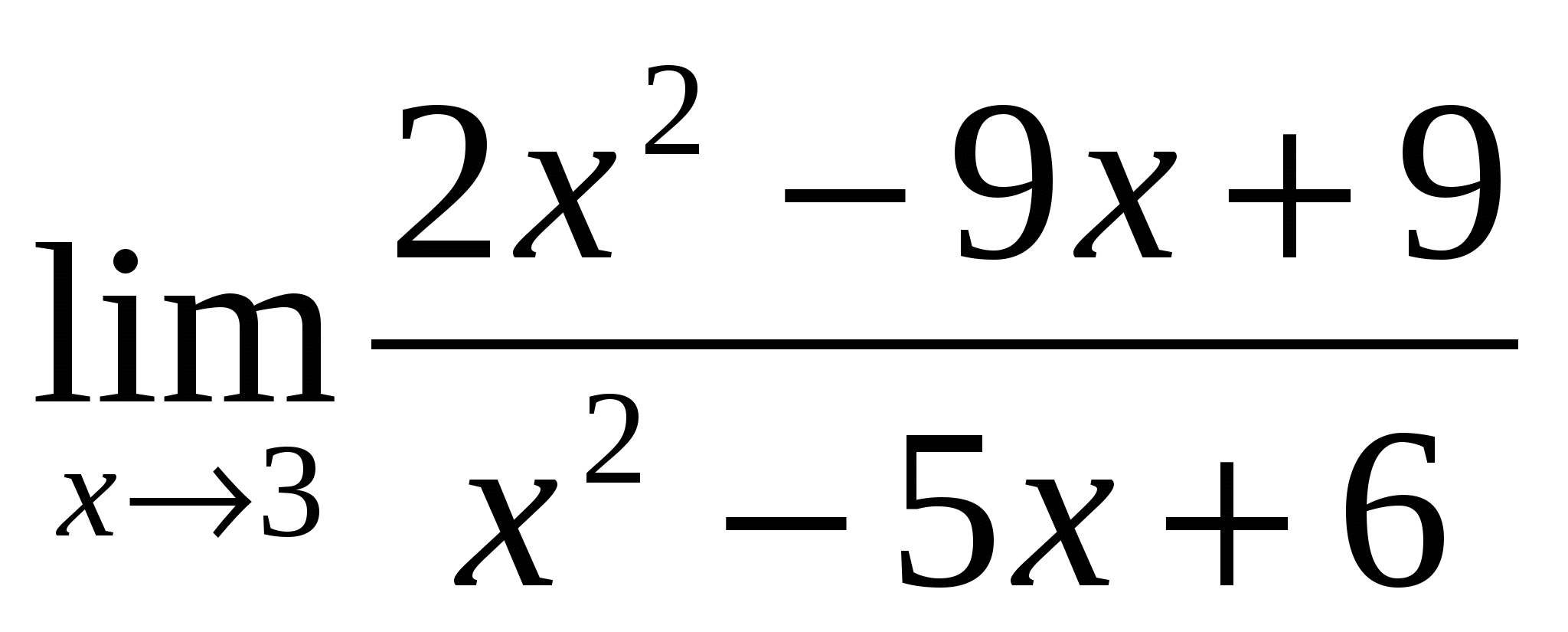 равен:
равен:
1) 2 2) 3 3) 0 4) ![]()
-
Объем первого цилиндра равен 4 см3. Найдите объем второго цилиндра, если при равных высотах, его диаметр в три раза больше, чем у первого.
1) 2 2) 12 3) 36 4) 24
-
Площадь полной поверхности куба равна 216 см2. Найдите длину ребра.
1) 6 2) 36 3) 16 4) 9
-
Общее количество граней у гексаэдра равно
1) 4 2) 6 3) 5 4) 8
-
Число размещений 6 элементов по 3 равно
1) 720 2) 320 3) 520 4) 120
При выполнении задания 12 – 16 укажите сначала номер задания, а затем запишите его решение.
-
Вычислите значение производной заданной функции при указанном значении независимой переменной:
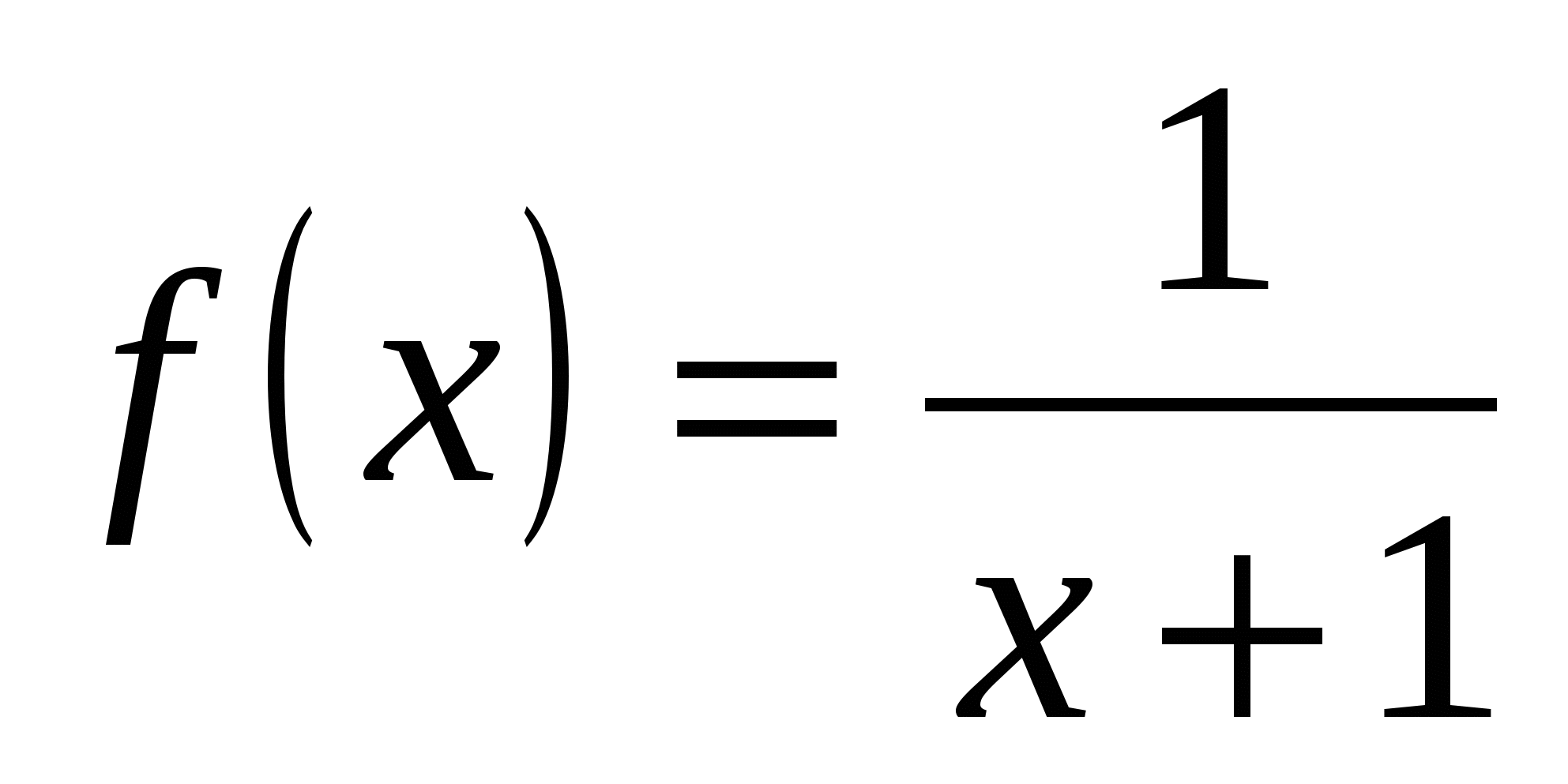 ;
; 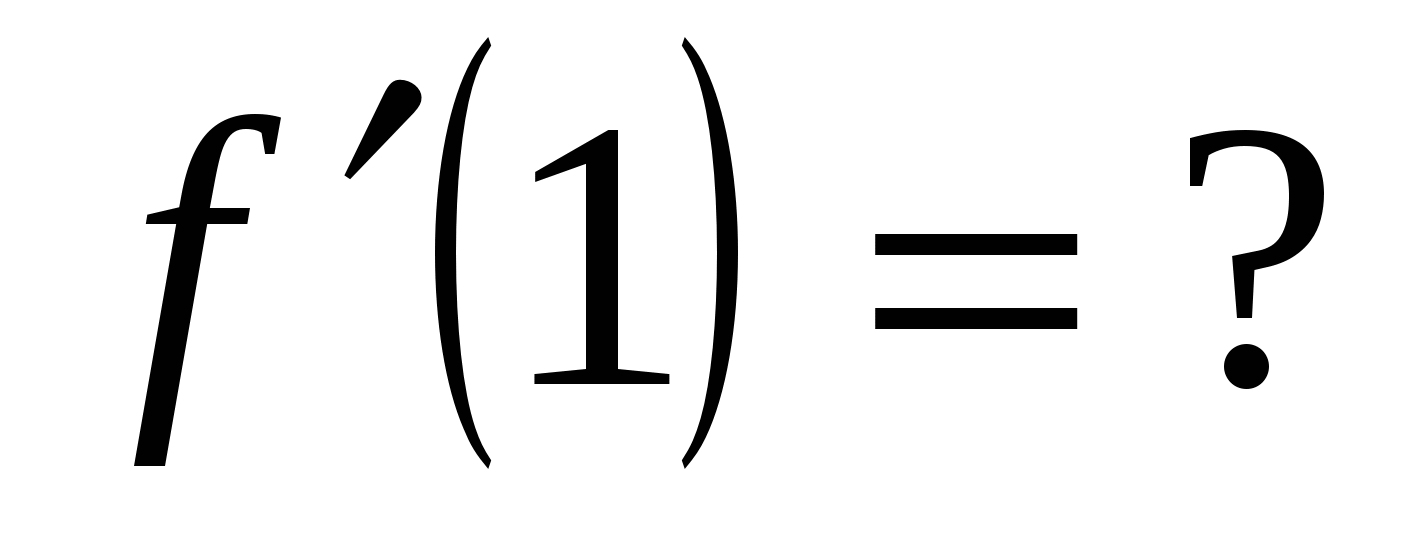
-
Найдите промежутки монотонности для функции
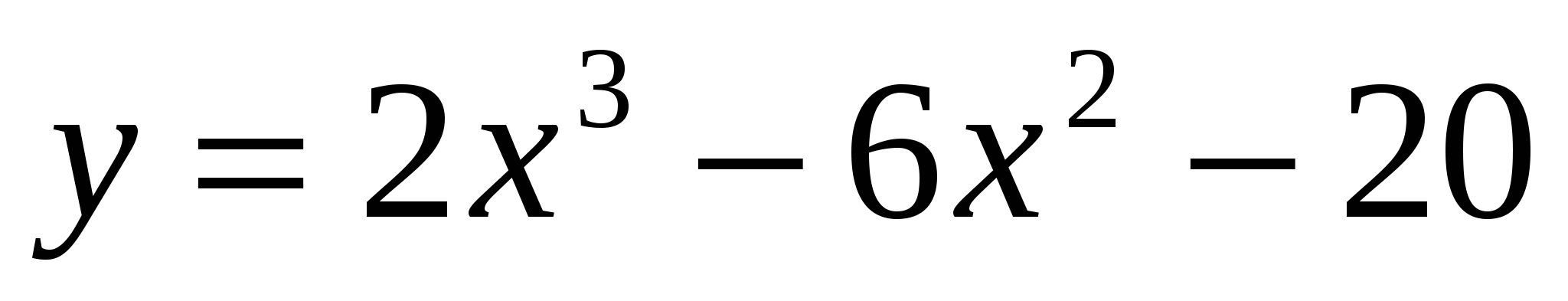 .
. -
Вычислите площадь фигуры, ограниченной заданными линиями
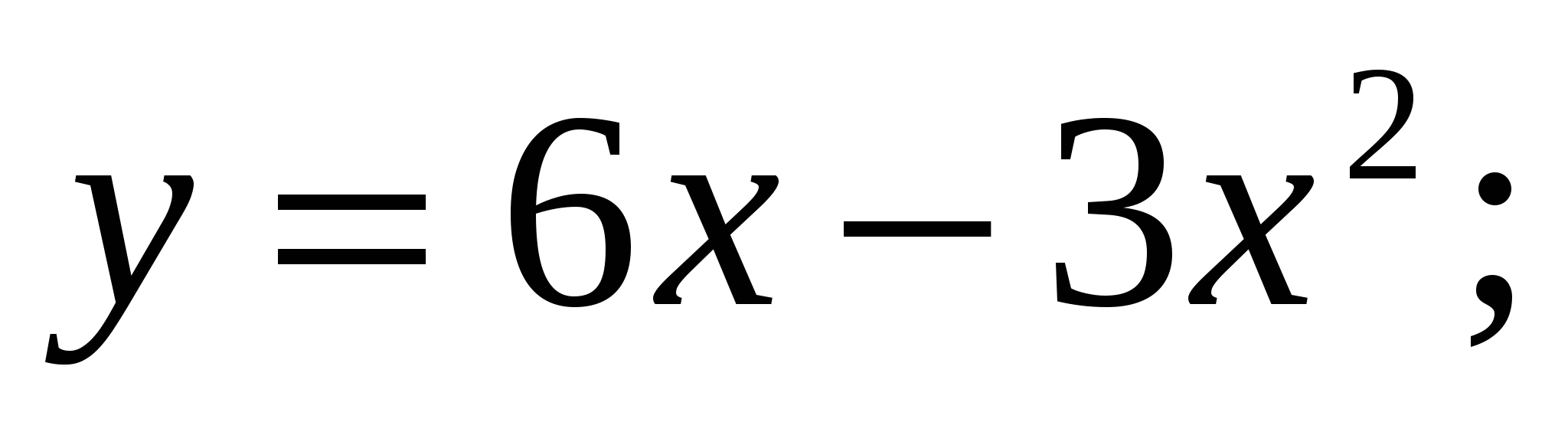
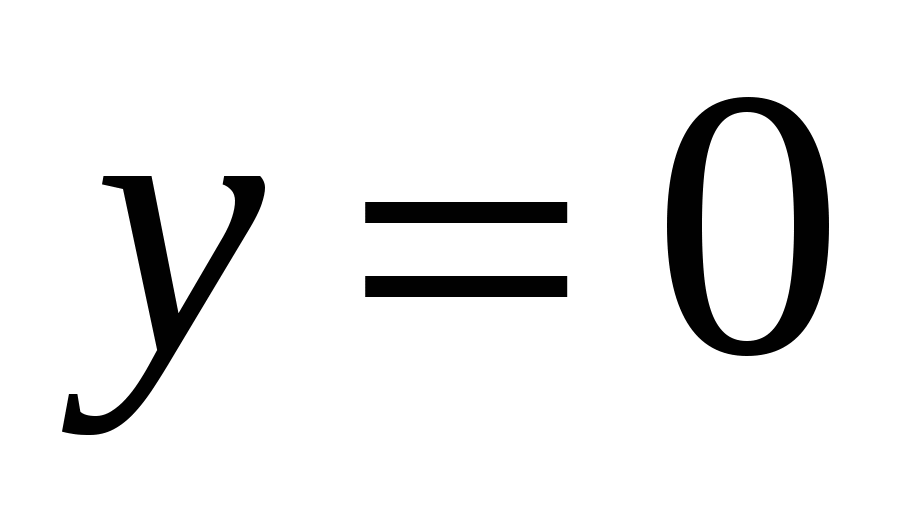 .
. -
Найдите значение выражения
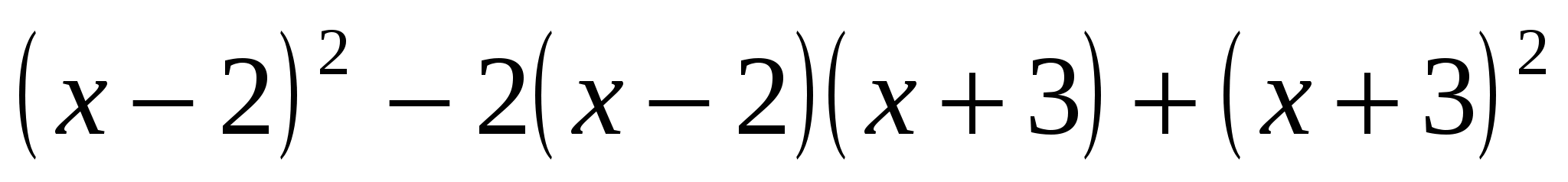 , при
, при 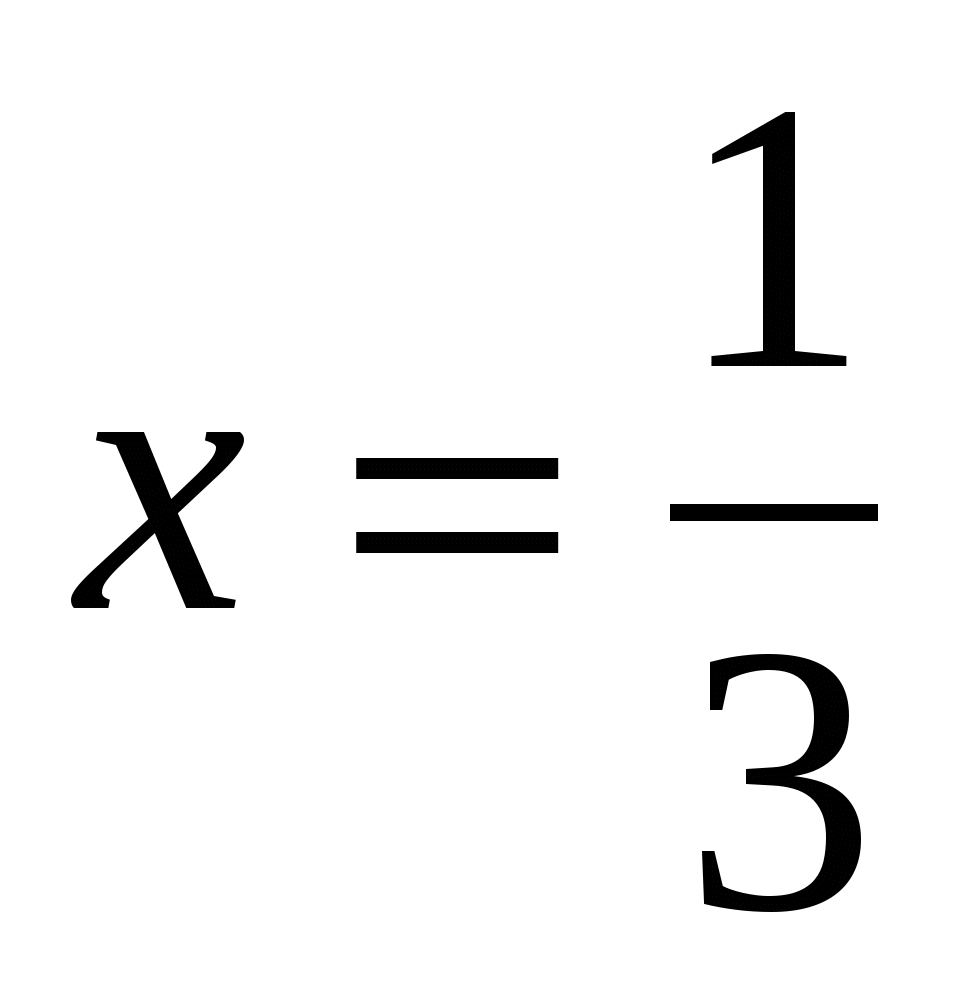 .
. -
Решите систему линейных уравнений методом Гаусса:
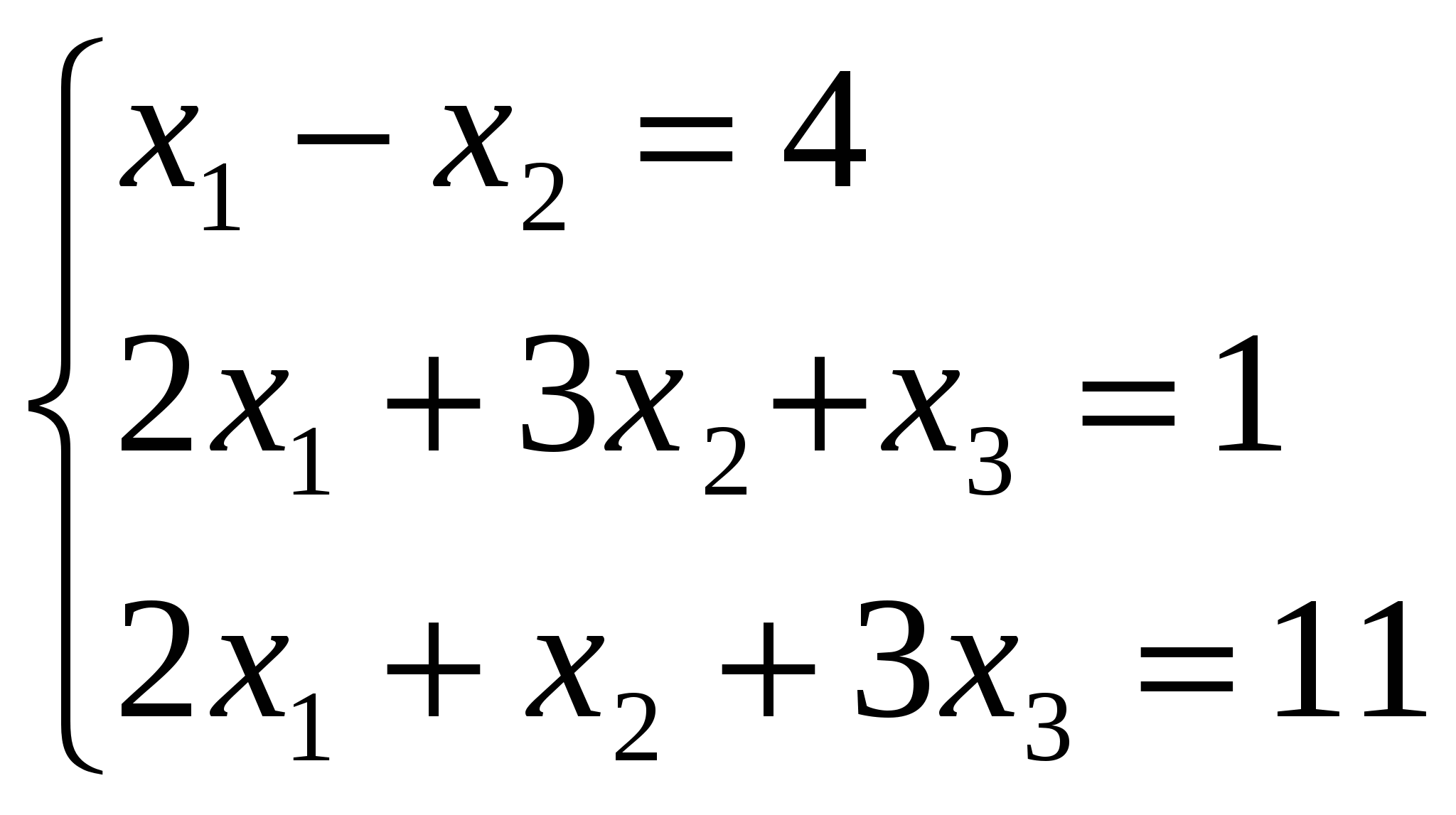
Вариант 6
При выполнении задания 1 – 11 в бланках ответа под номером соответствующего задания, поставьте номер правильного ответа.
-
Какое из указанных чисел является значением выражения
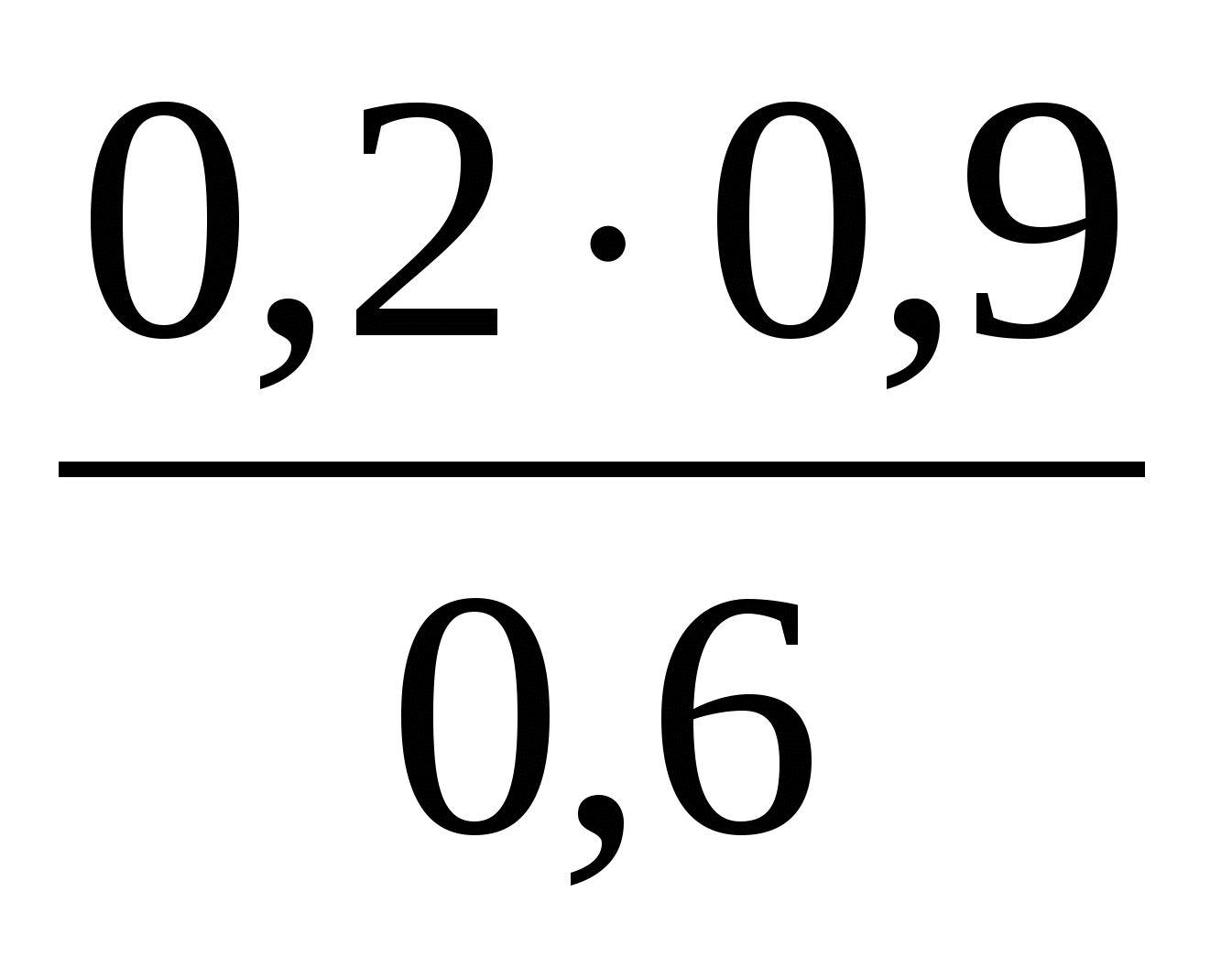 ?
?
1) 0,15 2) 3 3) 1,5 4) 0,3
-
Билет в кино стоит 300 рублей. Какое максимальное число билетов можно купить на 2500 рублей после повышения цены на 20%?
1) 8 2) 6 3) 5 4) 7
-
Найдите tg
 , если ctg
, если ctg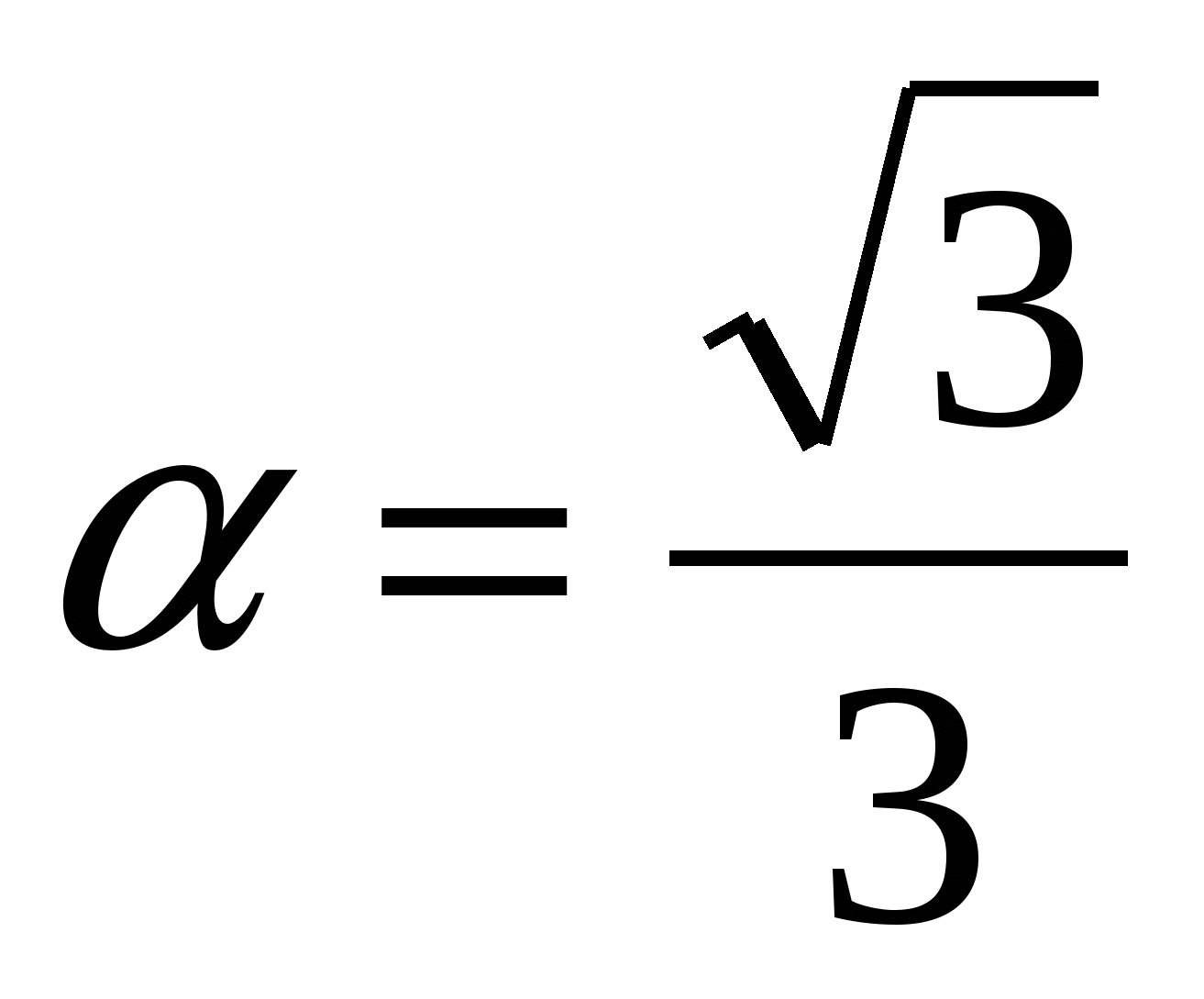 ,
, 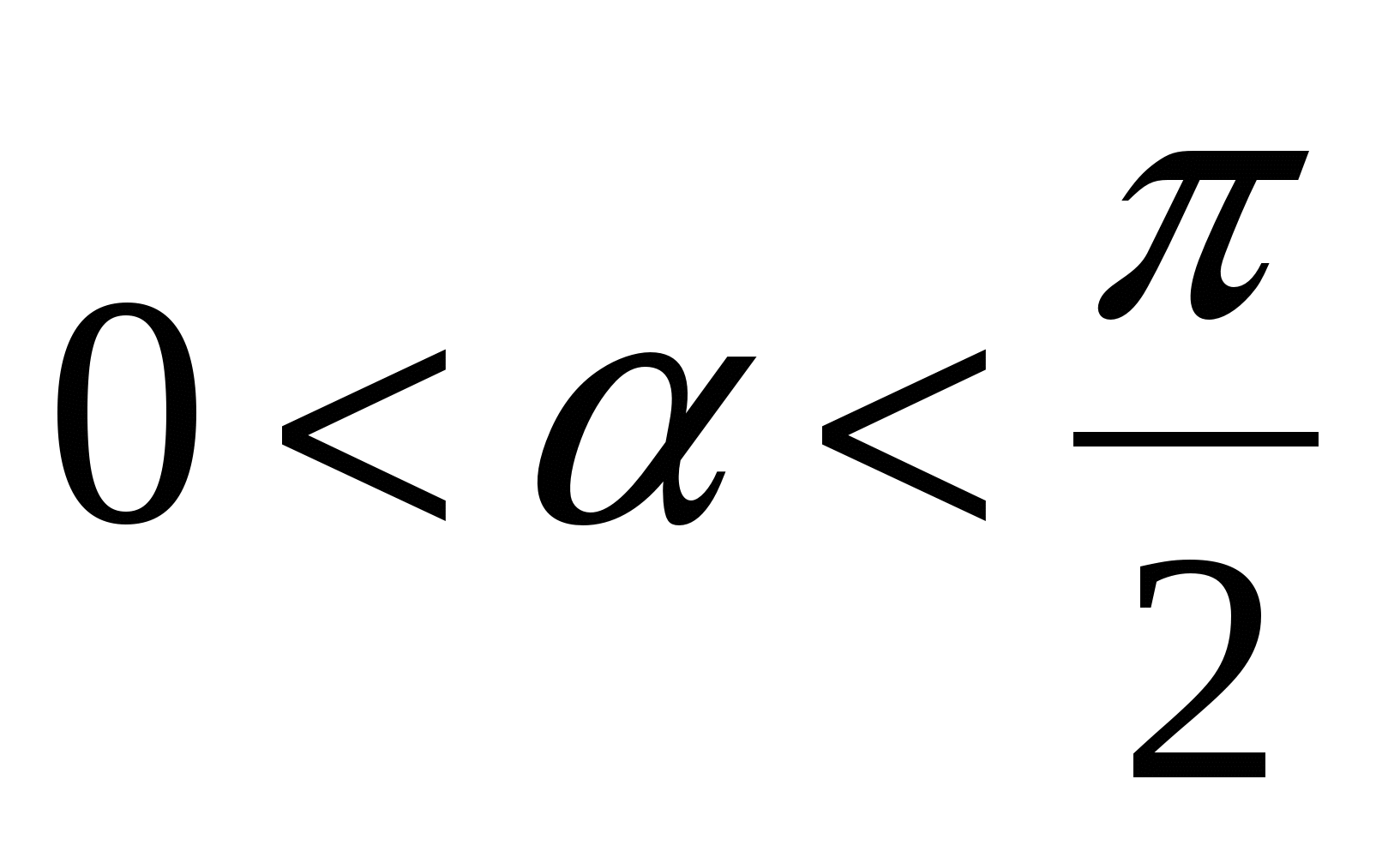 .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4) 1
4) 1
-
В сборнике по биологии всего 40 билетов, в шести из них встречаются вопросы о цветах. На экзамене школьнику достается один случайно выбранный билет из этого сборника. Какова вероятность того, что в этом билете не будет вопроса о цветах?
1) 0,15 2) 0,65 3) 0,95 4) 0,85
-
Упростите выражение и выберите правильный ответ
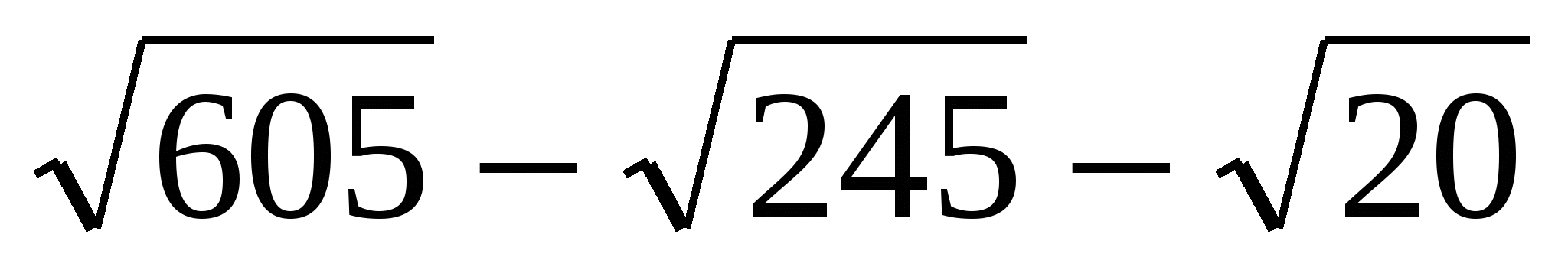 .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
-
Определите угловой коэффициент прямой
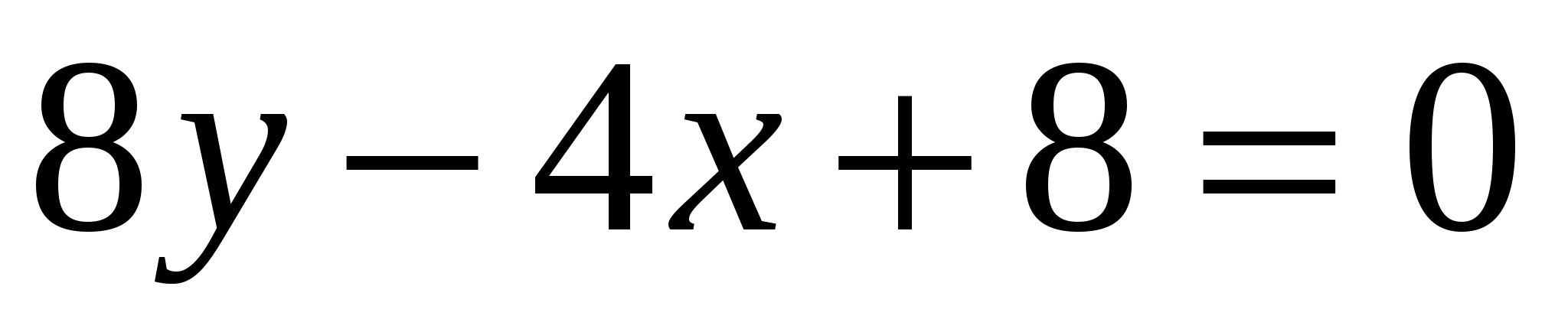 .
.
1) – 2 2) ![]() 3) 2 4)
3) 2 4)![]()
-
Предел функции
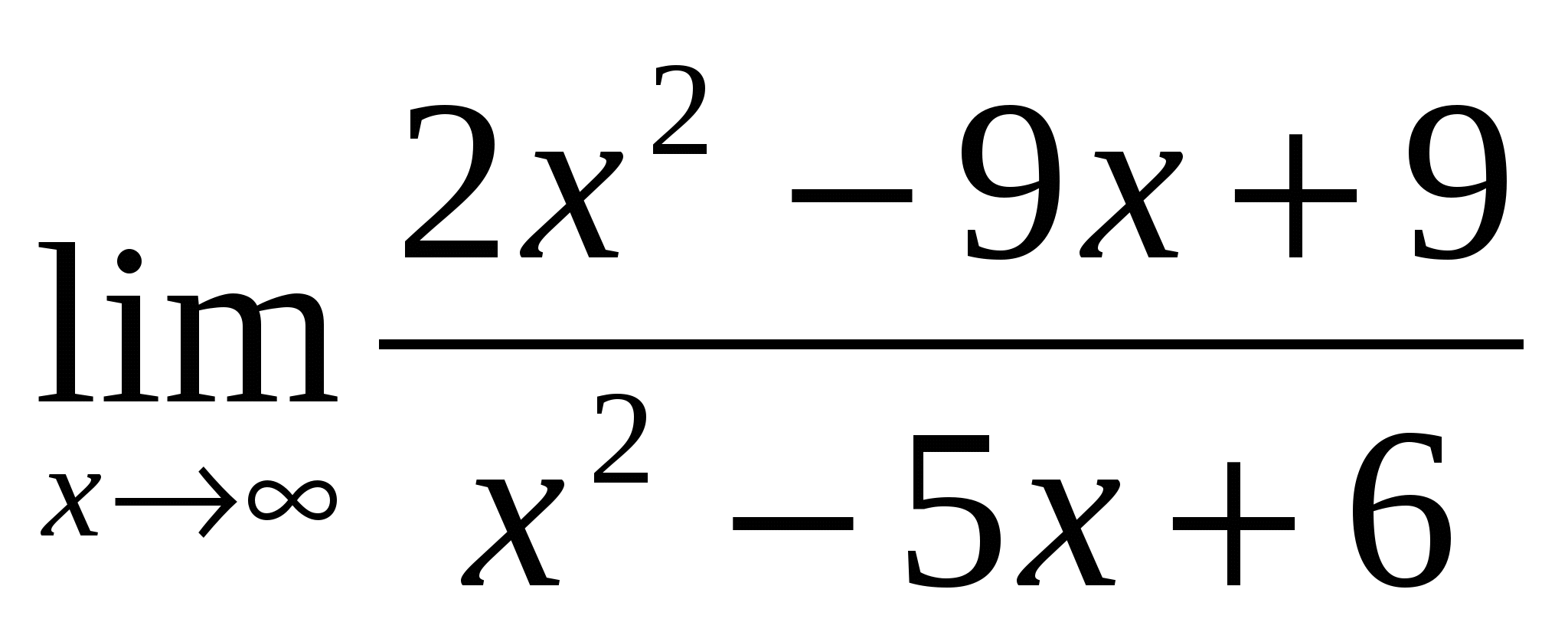 равен:
равен:
1) 2 2) ∞ 3) 0 4) ![]()
-
Объем первого цилиндра равен 36 см3. Найдите объем второго цилиндра, если при равных высотах, его радиус в три раза меньше, чем у первого.
1) 12 2) 18 3) 4 4) 8
-
Площадь полной поверхности куба равна 6 см2. Найдите длину ребра.
1) 6 2) 3 3) 2 4) 1
-
Общее количество вершин у икосаэдра равно
1) 8 2) 12 3) 20 4) 10
-
Число сочетаний 6 элементов по 3 равно
1) 20 2) 30 3) 10 4) 50
При выполнении задания 12 – 16 укажите сначала номер задания, а затем запишите его решение.
-
Вычислите значение производной заданной функции при указанном значении независимой переменной:
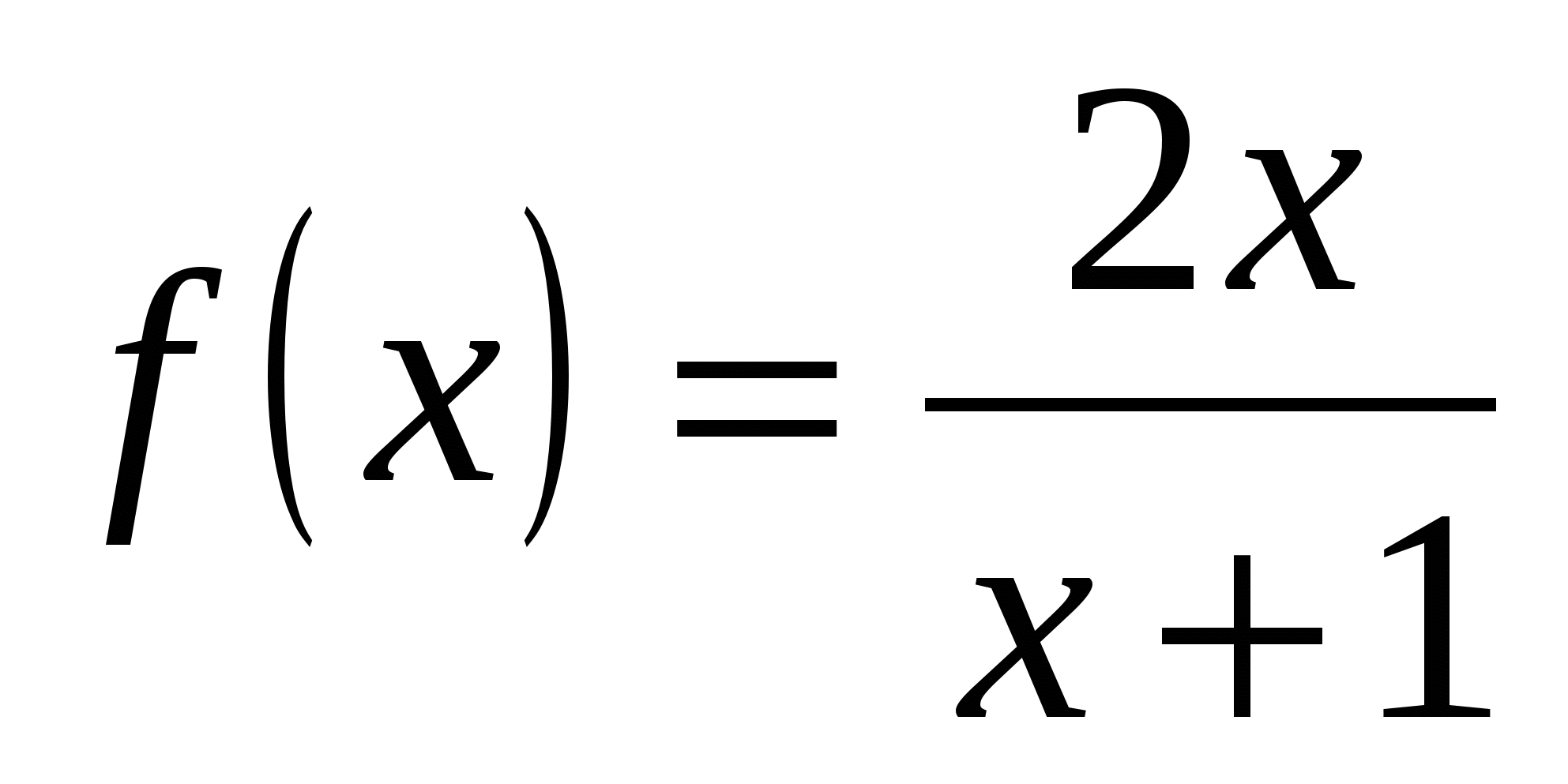 ;
; 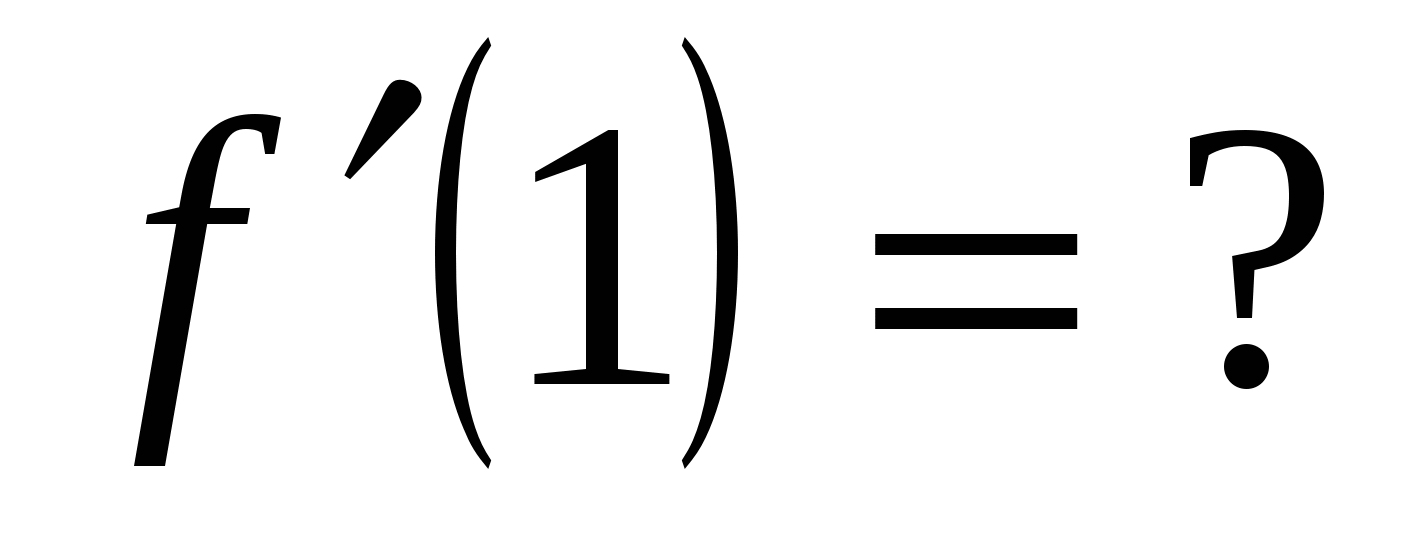
-
Найдите промежутки монотонности для функции
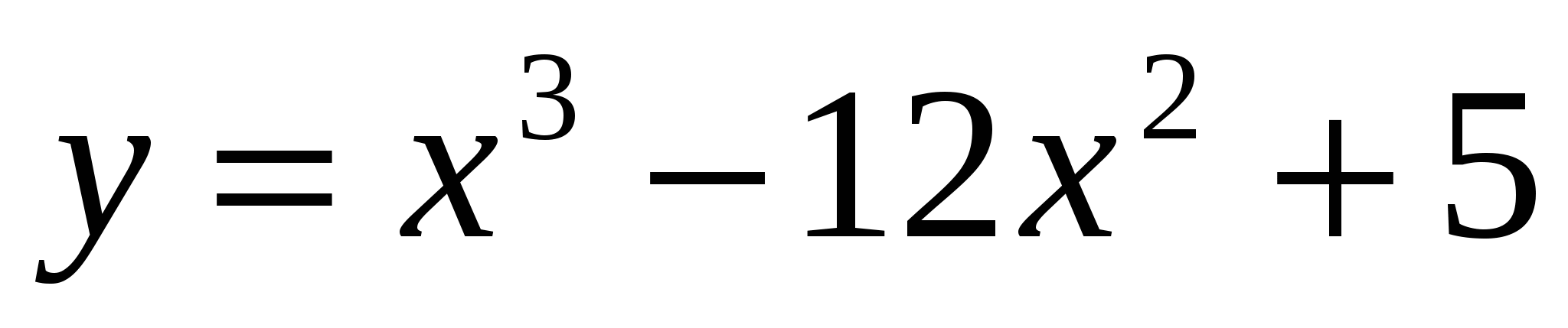 .
. -
Вычислите площадь фигуры, ограниченной заданными линиями
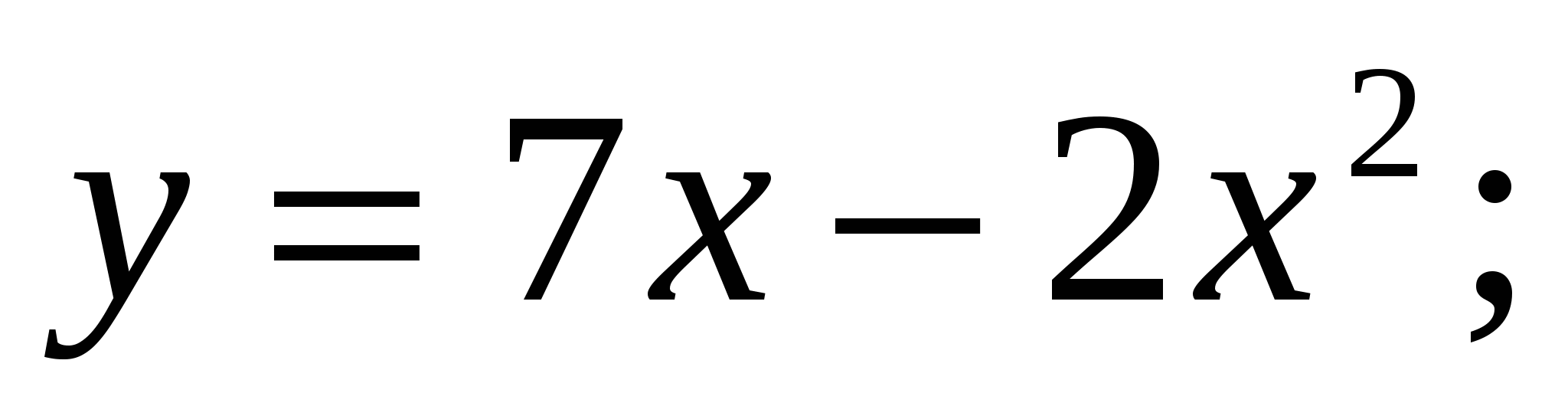
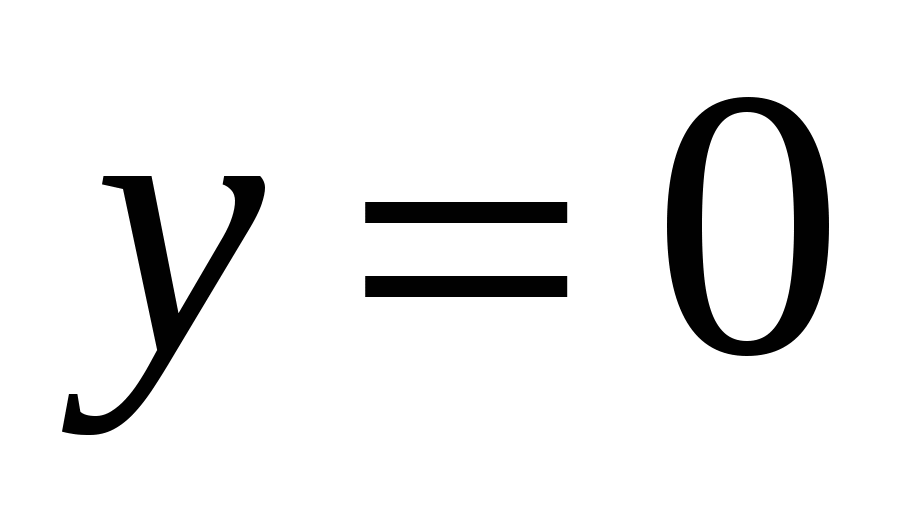 .
. -
Найдите значение выражения
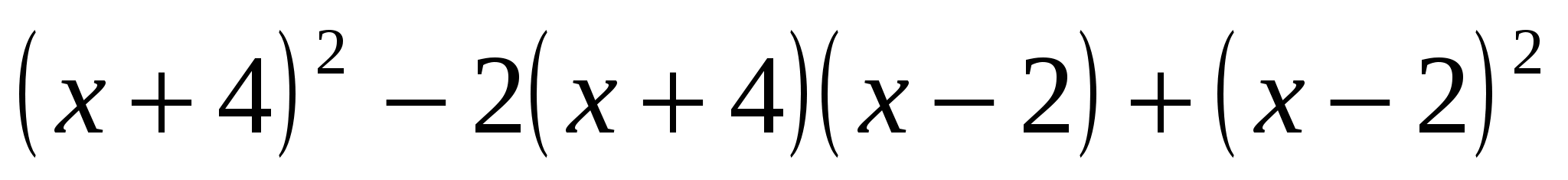 , при
, при 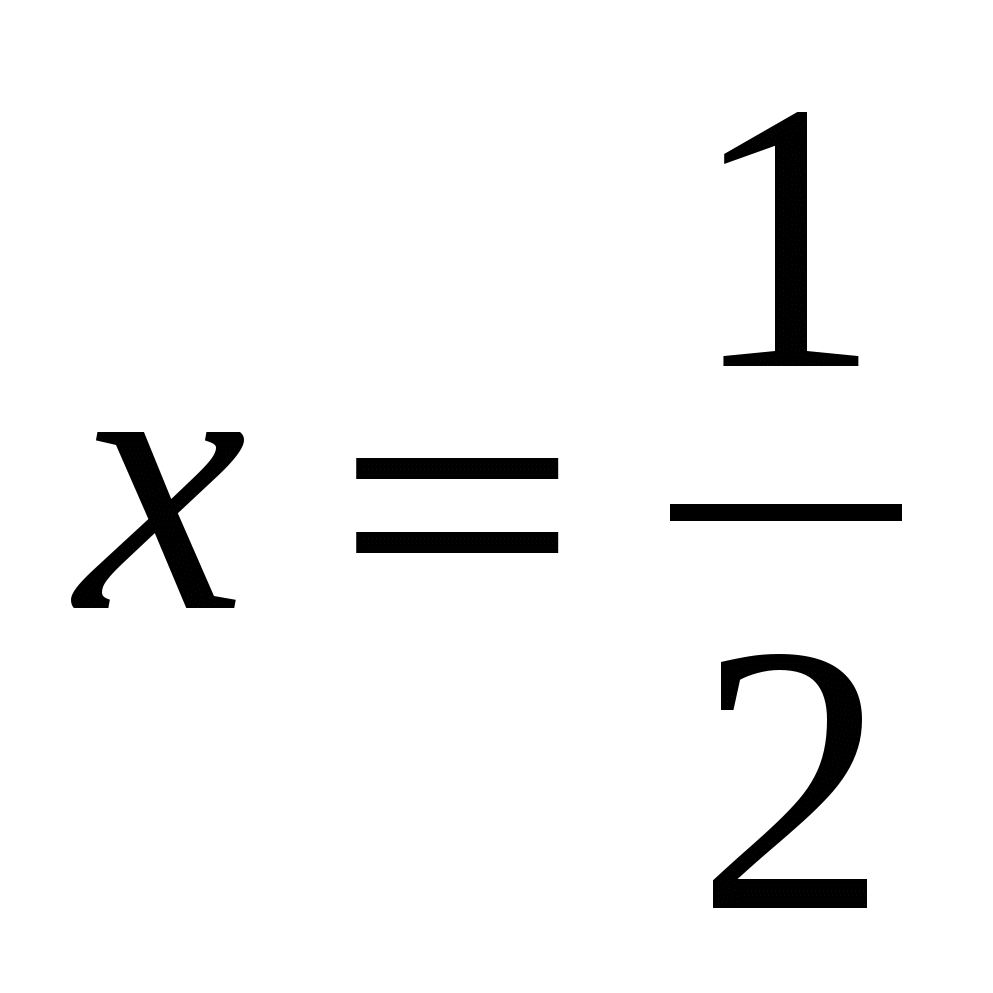 .
. -
Решите систему линейных уравнений методом Крамера:
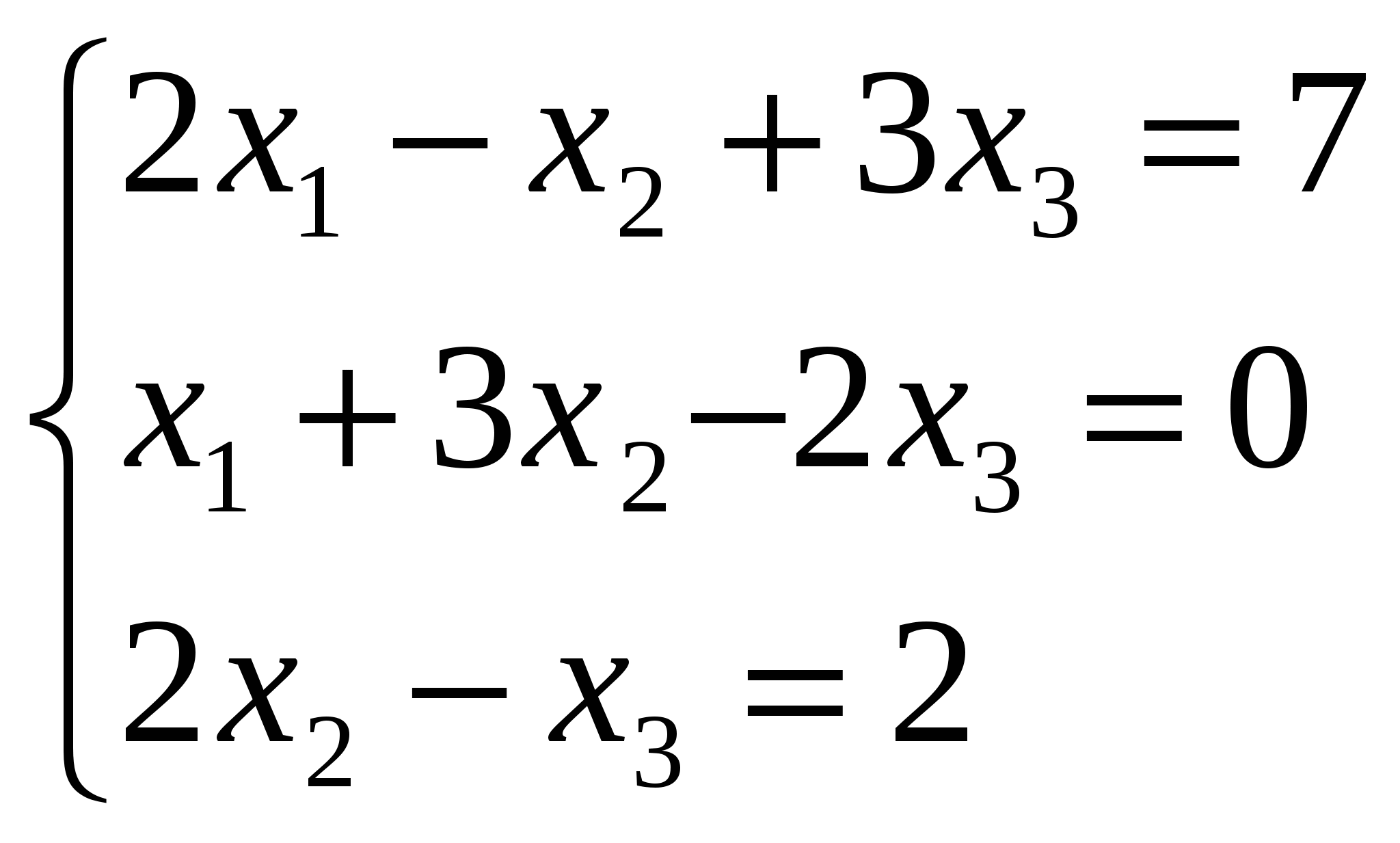
Вариант 7
При выполнении задания 1 – 11 в бланках ответа под номером соответствующего задания, поставьте номер правильного ответа.
-
Какое из указанных чисел является значением выражения
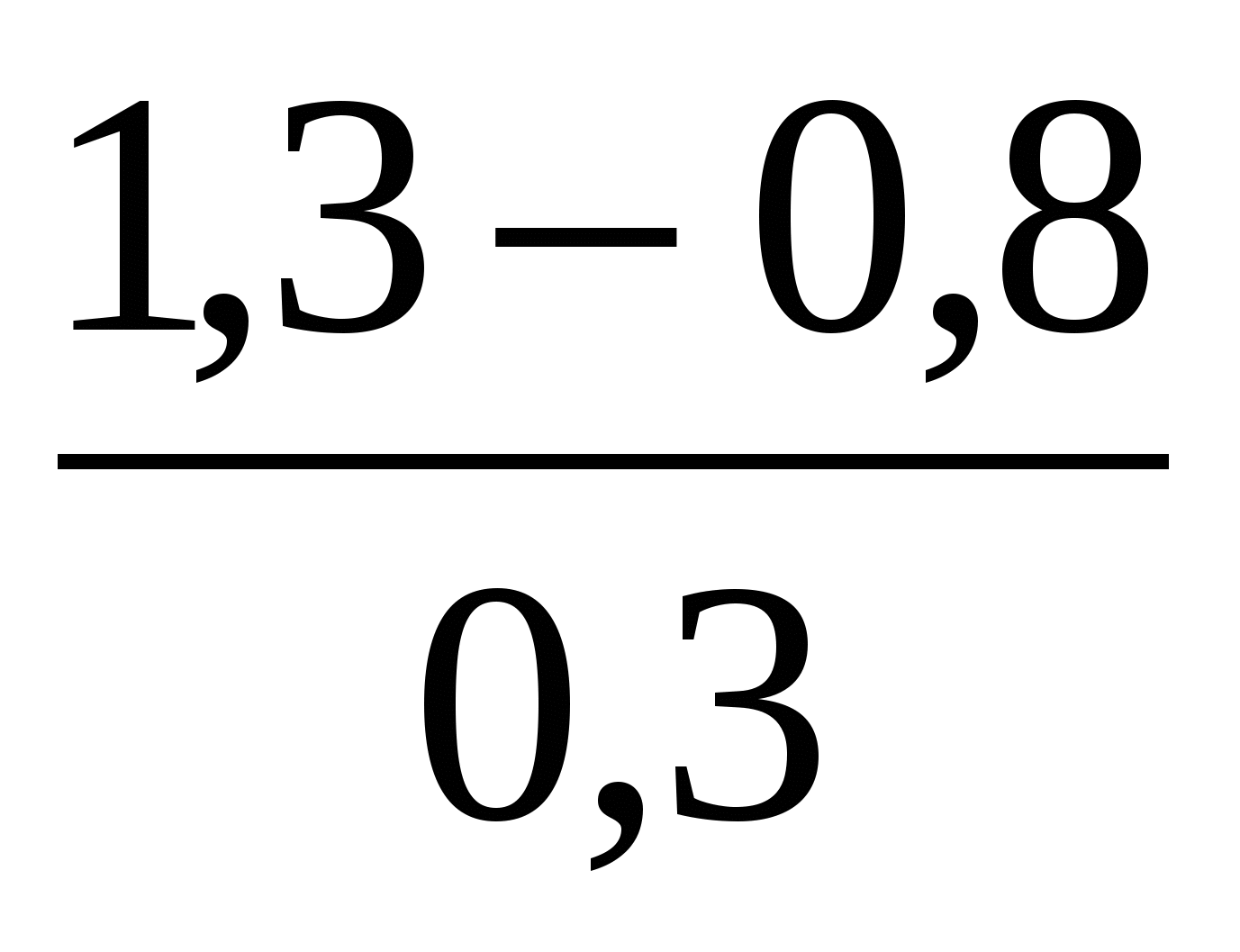 ?
?
1) 1,6 2) ![]() 3) 0,6 4)
3) 0,6 4) ![]()
-
Билет в кино стоит 120 рублей. Какое максимальное число билетов можно купить на 1000 рублей после повышения цены на 15%?
1) 4 2) 6 3) 5 4) 7
-
Найдите ctg
 , если tg
, если tg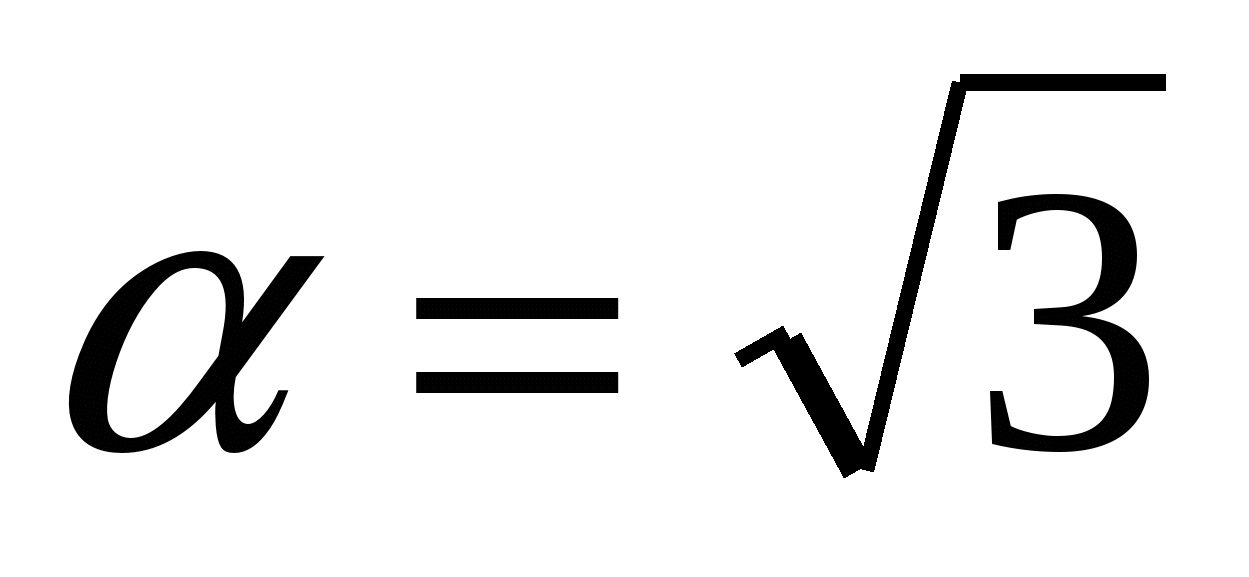 ,
, 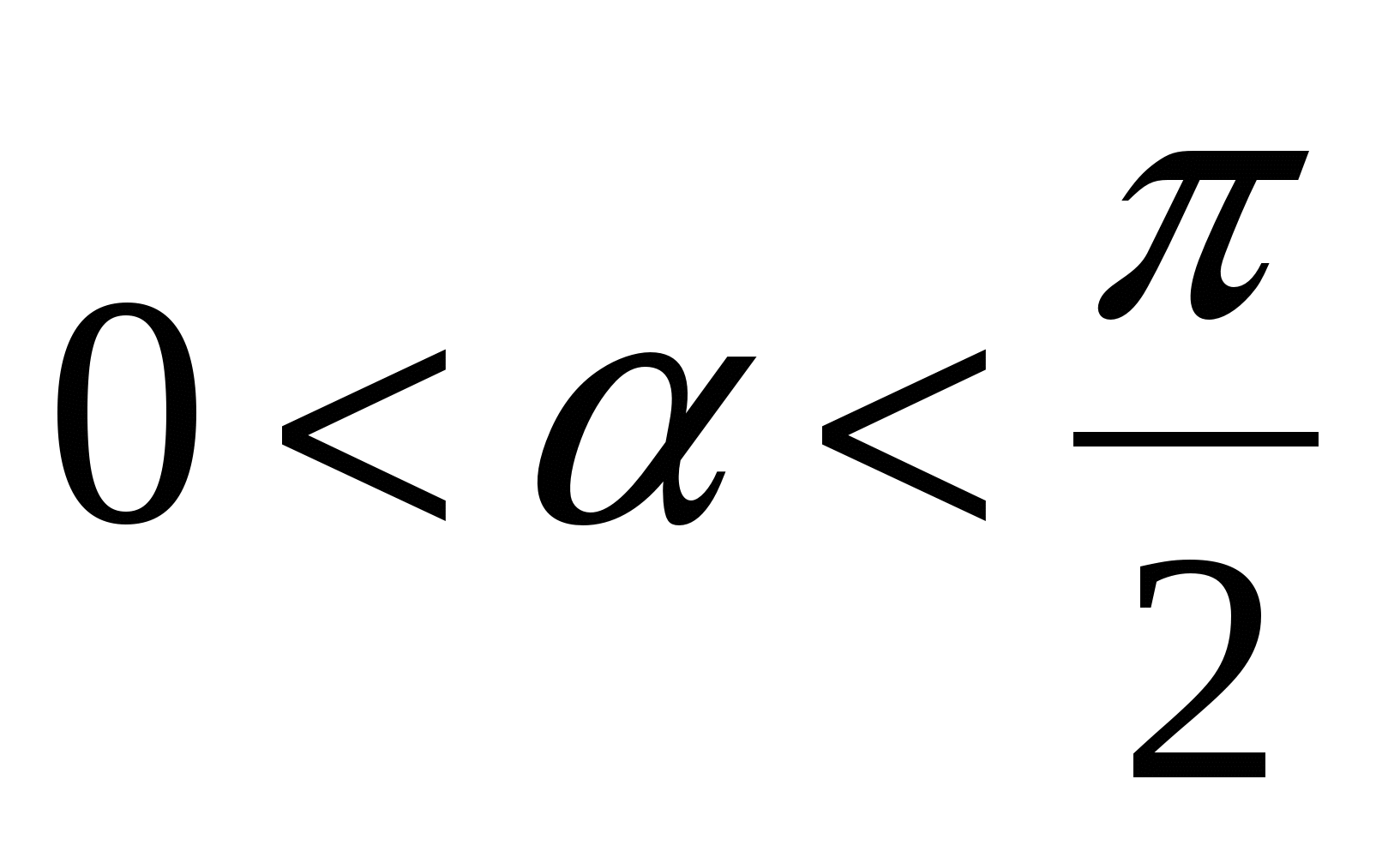 .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4) 1
4) 1
-
В сборнике по биологии всего 35 билетов, в семи из них встречается вопрос о цветах. На экзамене школьнику достается один случайно выбранный билет из этого сборника. Какова вероятность того, что в этом билете будет вопрос о цветах?
1) 0,8 2) 0,2 3) 0,5 4) 0,6
-
Упростите выражение и выберите правильный ответ
 .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
-
Определите угловой коэффициент прямой
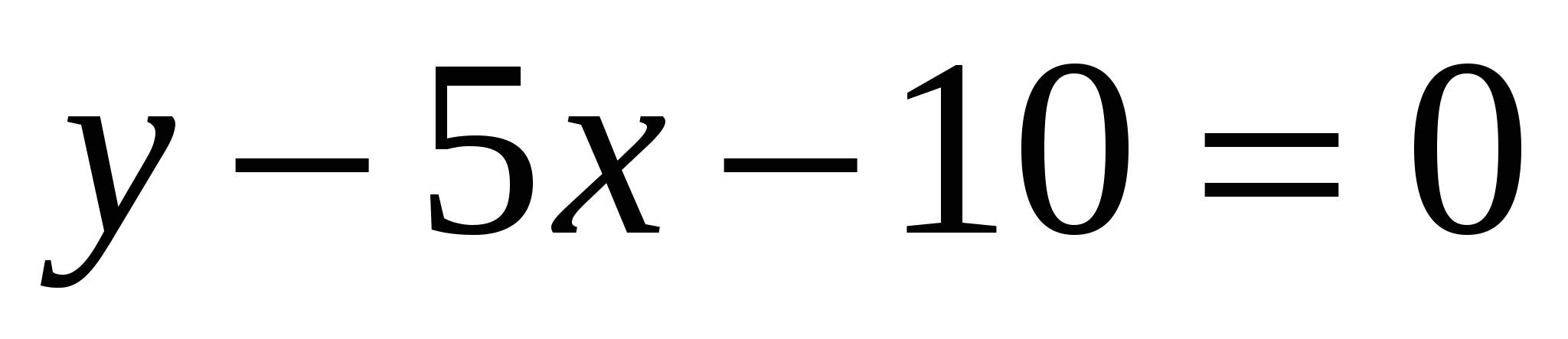 .
.
1) – 5 2) ![]() 3) 5 4)
3) 5 4)![]()
-
Предел функции
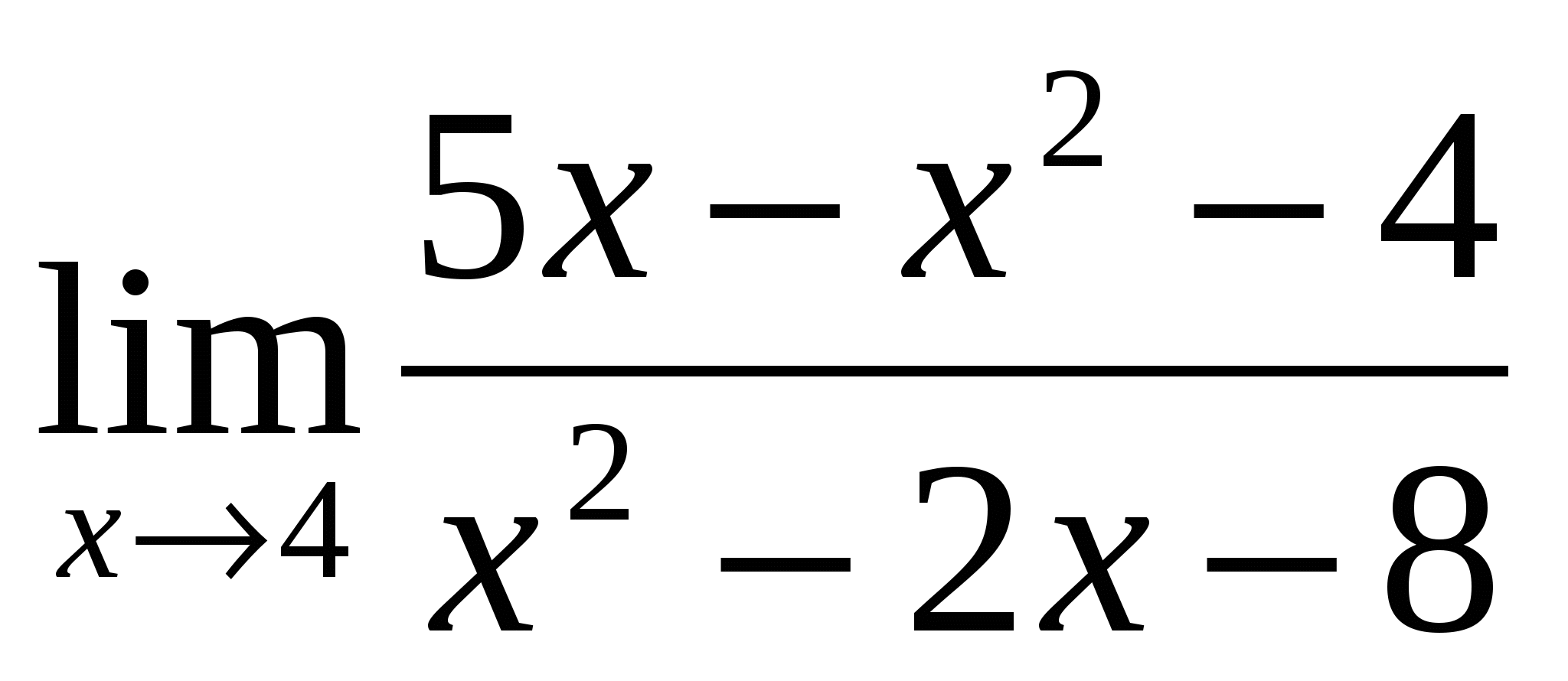 равен:
равен:
1) 5 2) ![]() 3) 0 4)
3) 0 4) ![]()
-
Объем первого цилиндра равен 20 см3. Найдите объем второго цилиндра, если при равных высотах, его радиус в два раза меньше, чем у первого.
1) 2,5 2) 5 3) 40 4) 20
-
Площадь полной поверхности куба равна 0,24 см2. Найдите длину ребра.
1) 0,4 2) 0,12 3) 0,2 4) 0,8
-
Общее количество граней у додекаэдра равно
1) 14 2) 16 3) 12 4) 18
-
Число размещений 4 элементов по 2 равно
1) 3 2) 4 3) 8 4) 12
При выполнении задания 12 – 16 укажите сначала номер задания, а затем запишите его решение.
-
Вычислите значение производной заданной функции при указанном значении независимой переменной:
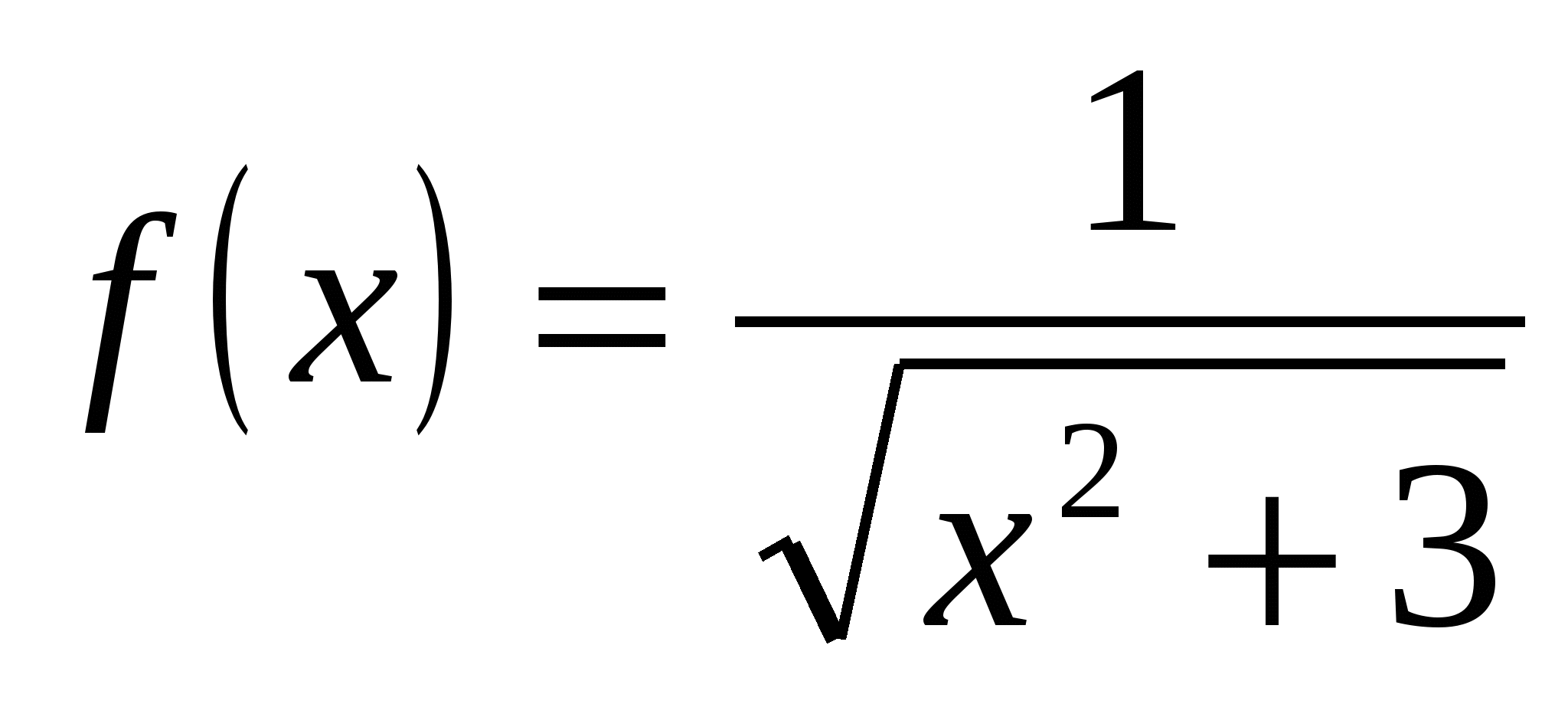 ;
; 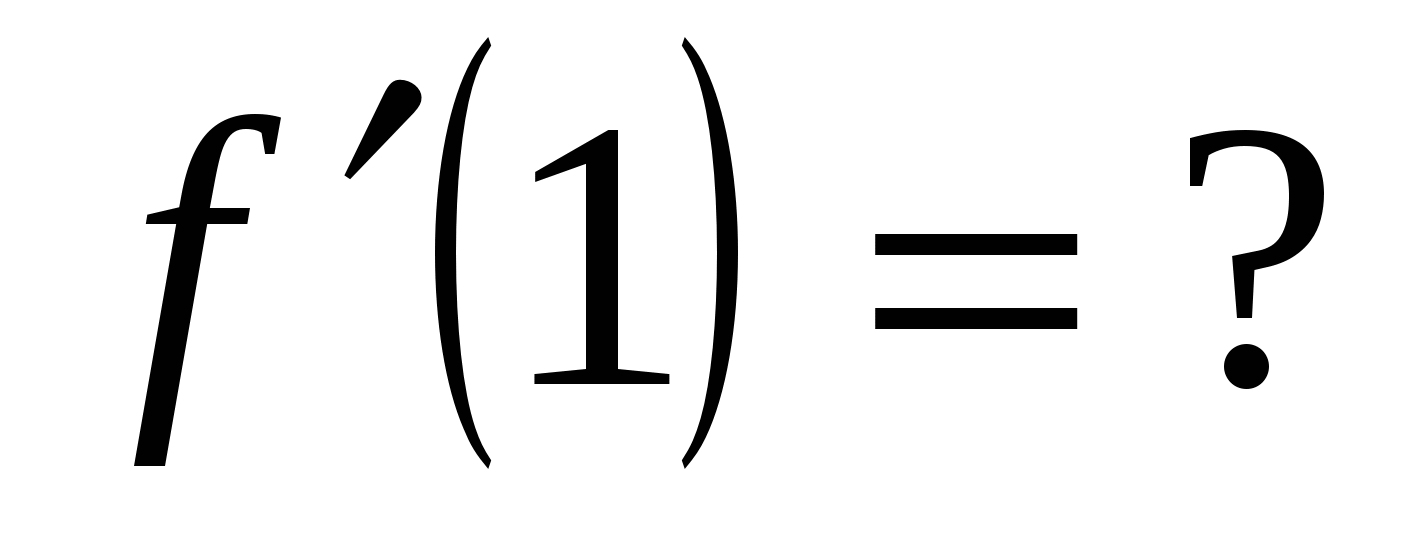
-
Найдите промежутки монотонности для функции
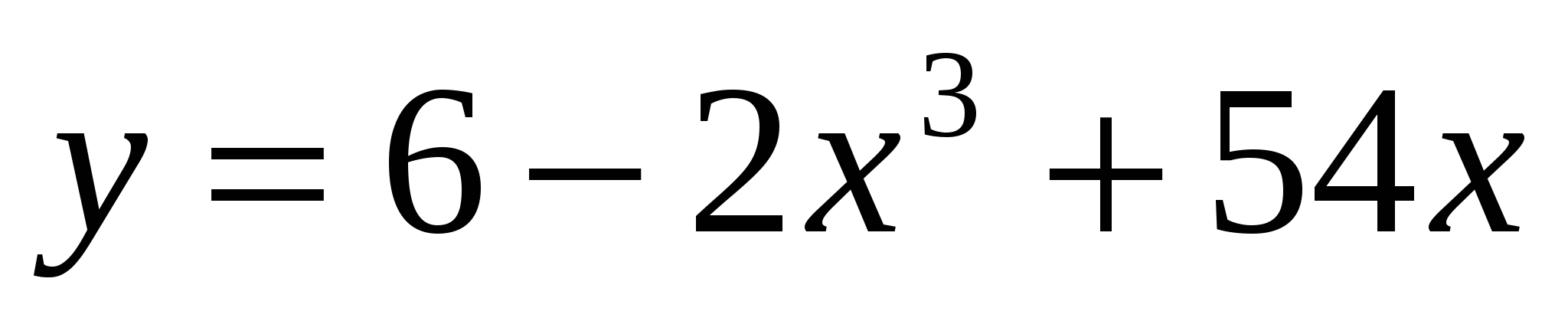 .
. -
Вычислите площадь фигуры, ограниченной заданными линиями
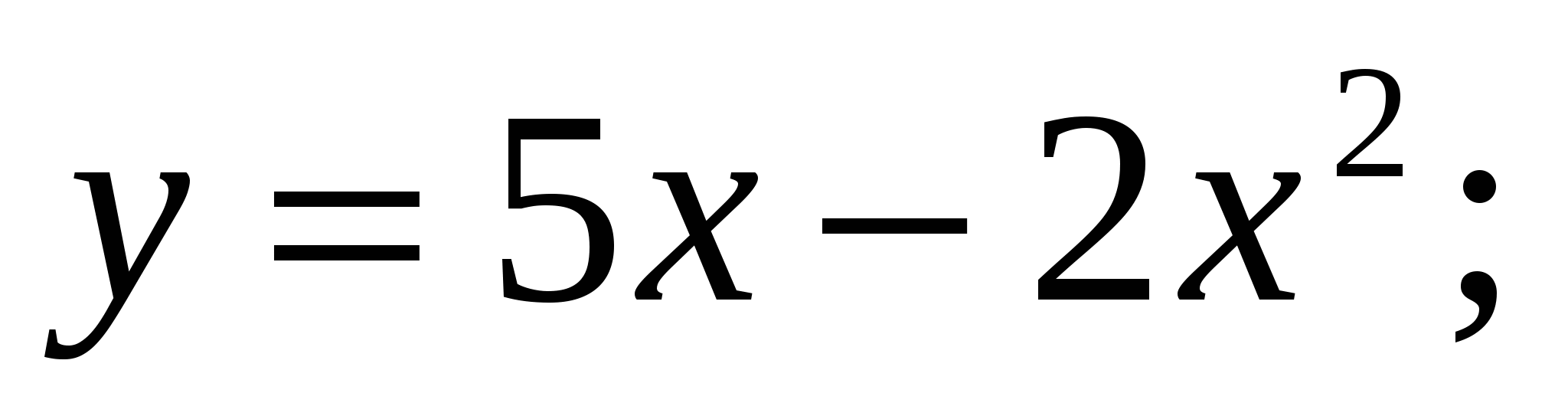
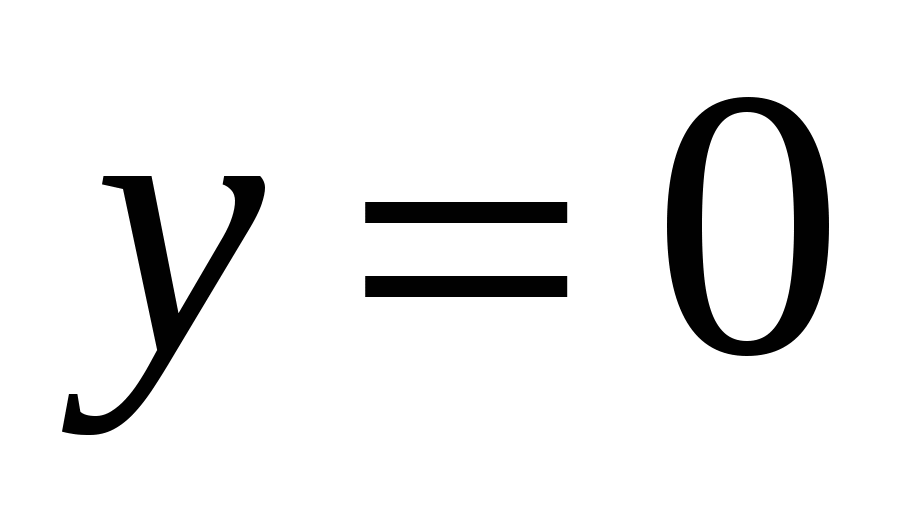 .
. -
Найдите значение выражения
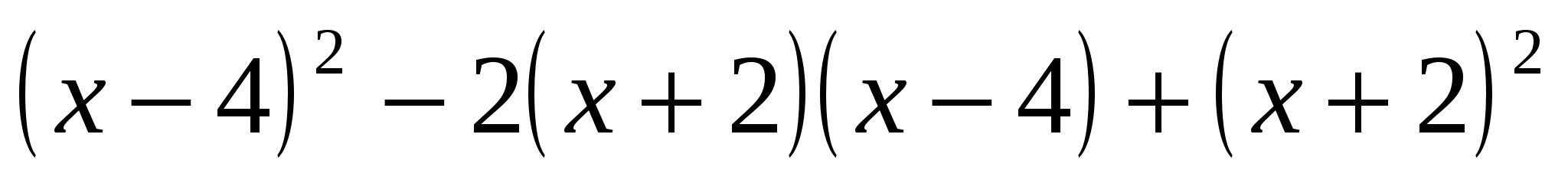 , при
, при 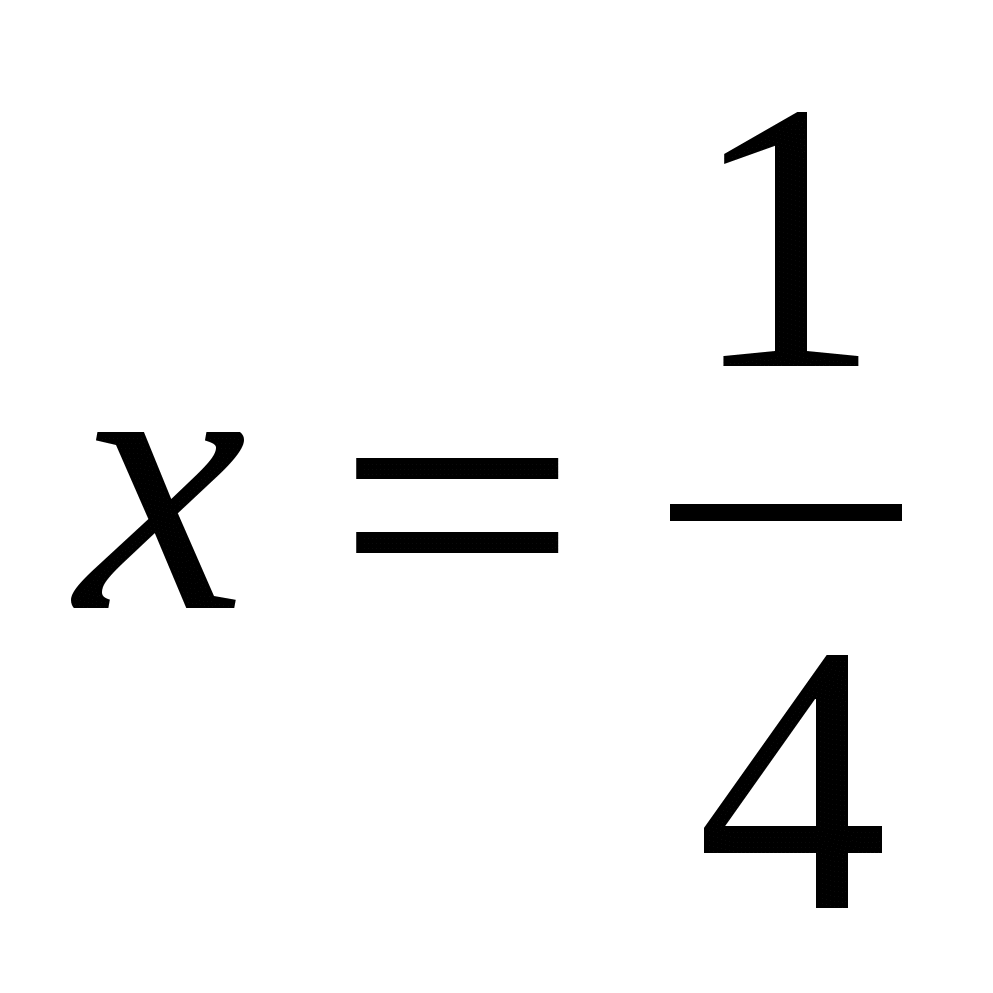 .
. -
Решите систему линейных уравнений методом Крамера:
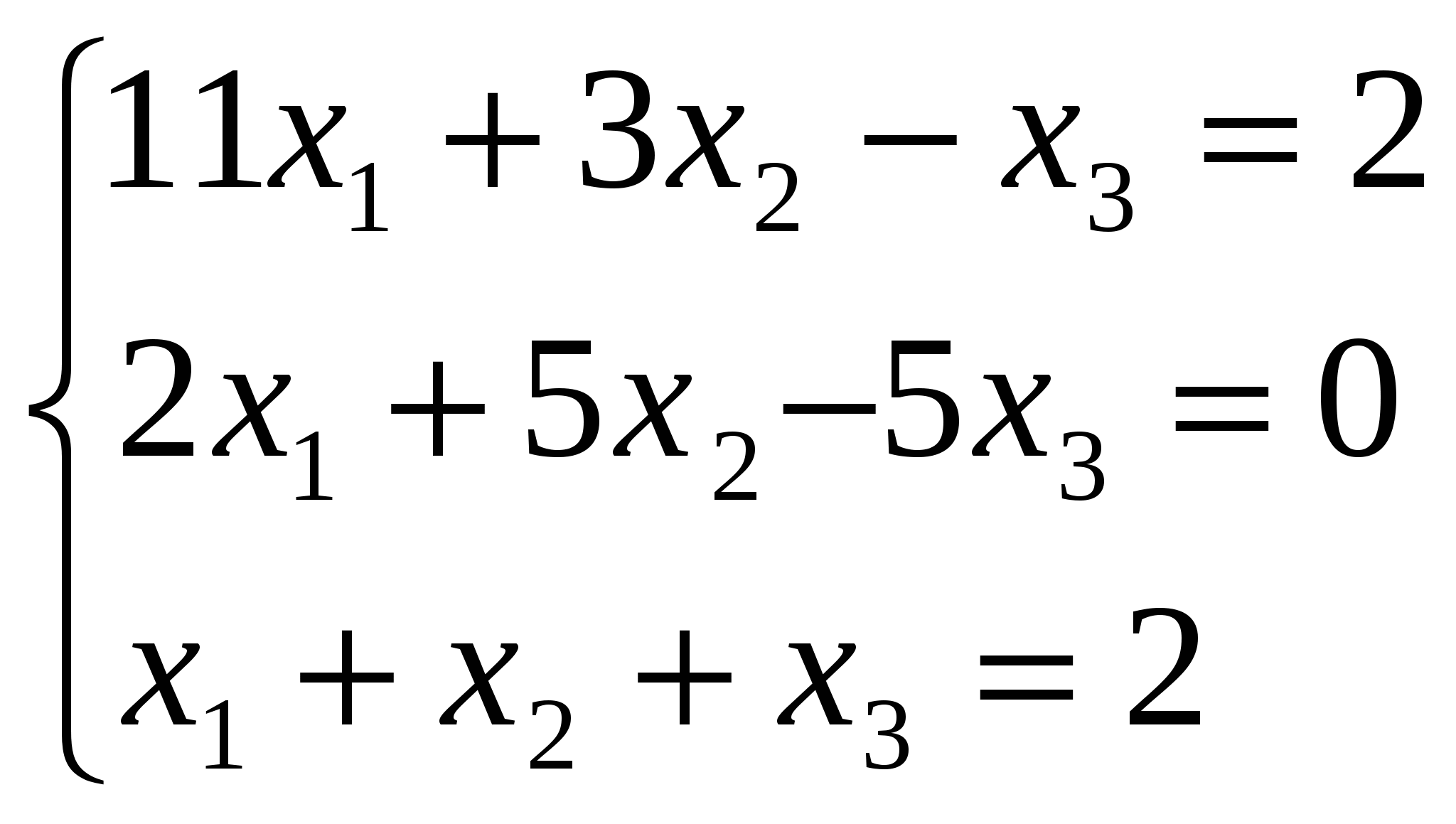
Вариант 8
При выполнении задания 1 – 11 в бланках ответа под номером соответствующего задания, поставьте номер правильного ответа.
-
Какое из указанных чисел является значением выражения
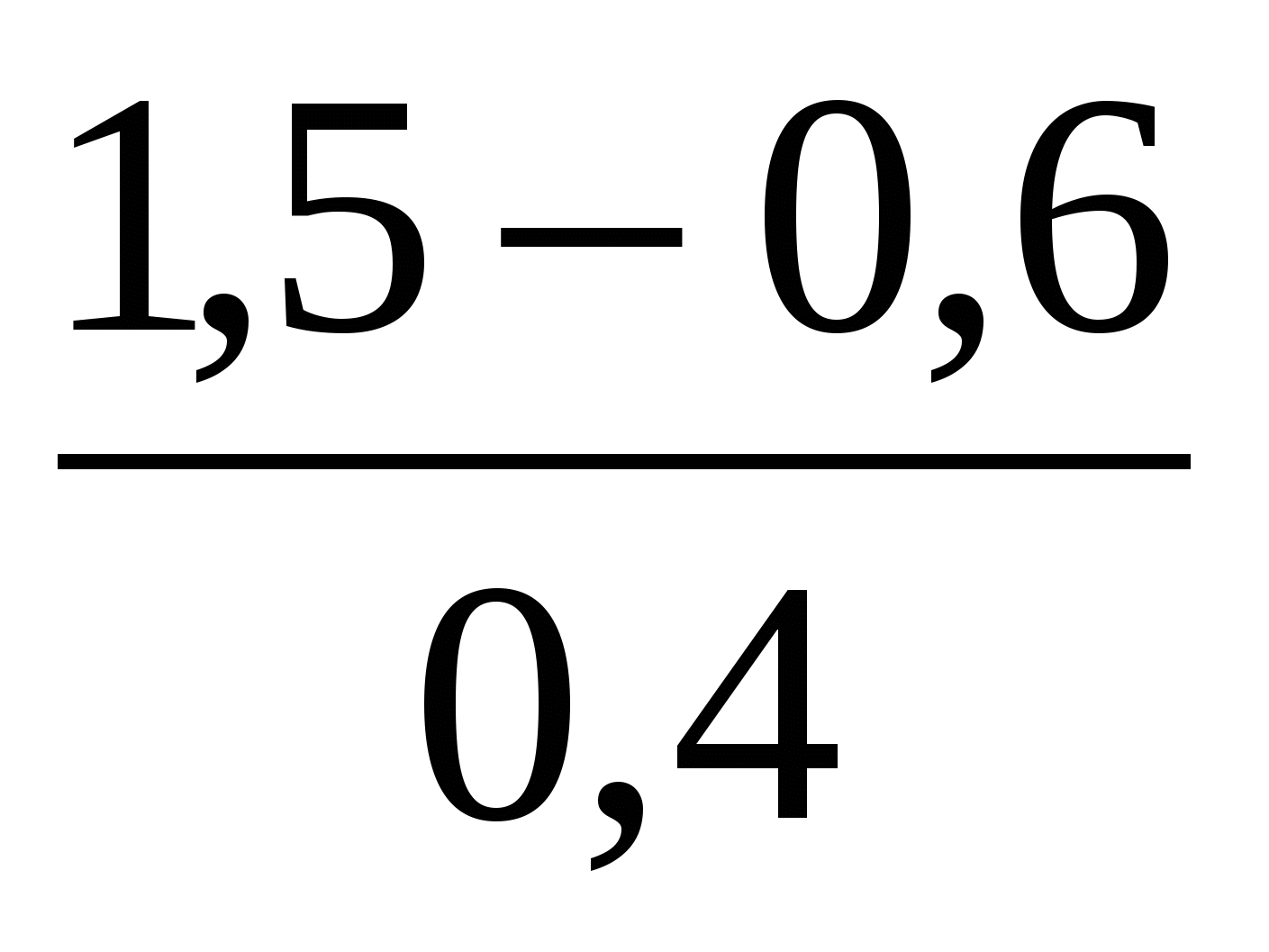 ?
?
1) ![]() 2) 2,5 3)
2) 2,5 3) ![]() 4) 2,2
4) 2,2
-
Билет в театр стоит 120 рублей. Какое максимальное число билетов можно купить на 1000 рублей после повышения цены на 10%?
1) 4 2) 6 3) 5 4) 7
-
Найдите tg
 , если ctg
, если ctg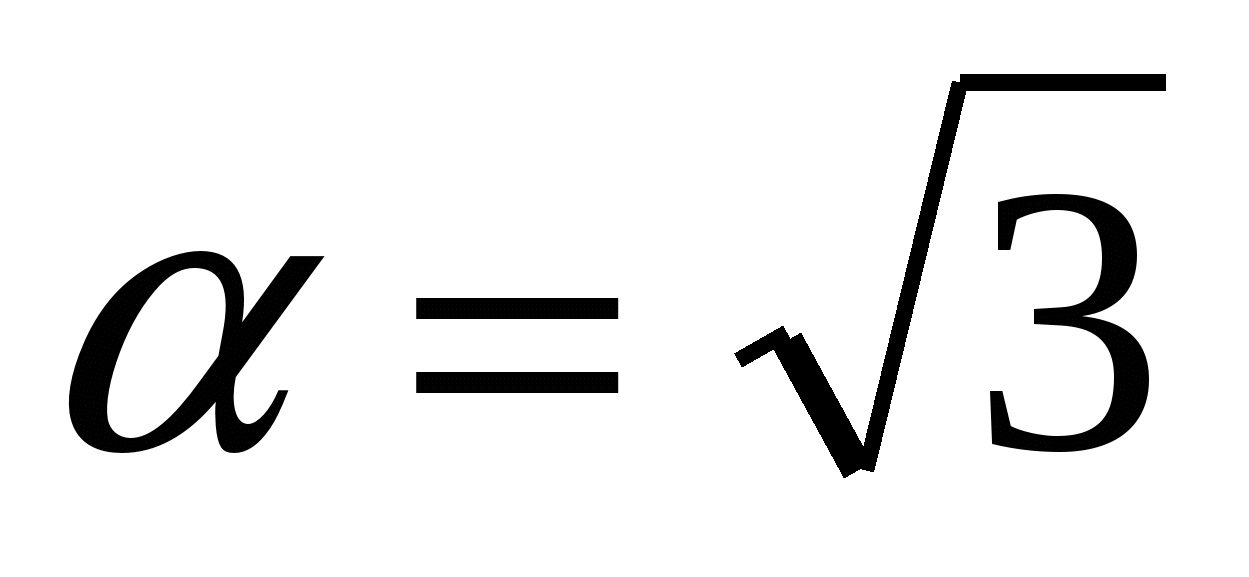 ,
, 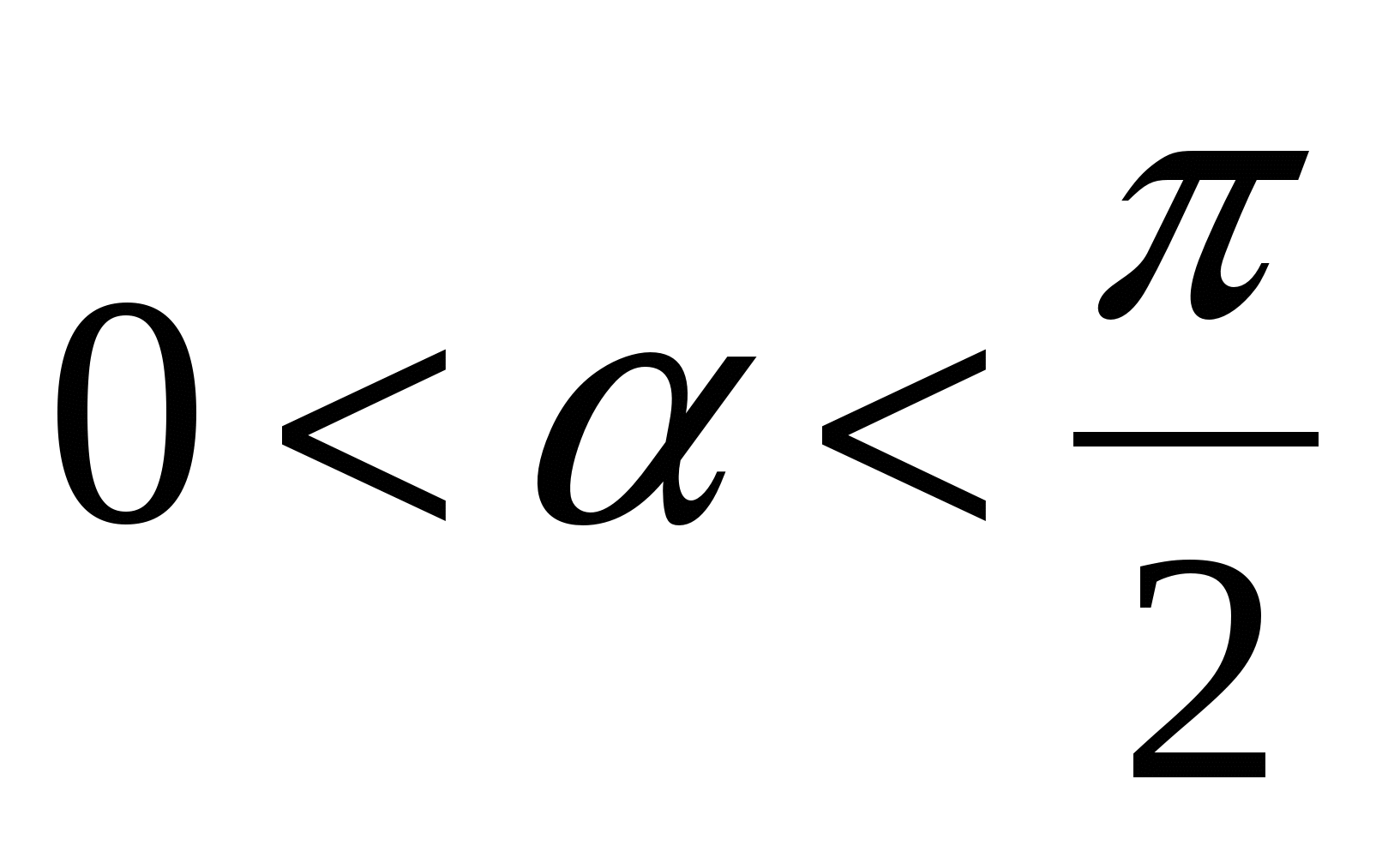 .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4) 1
4) 1
-
В сборнике по физике всего 30 билетов, в девяти из них встречается вопрос о линзах. На экзамене школьнику достается один случайно выбранный билет из этого сборника. Какова вероятность того, что в этом билете не будет вопроса о линзах?
1) 0,2 2) 0,7 3) 0,5 4) 0,3
-
Упростите выражение и выберите правильный ответ
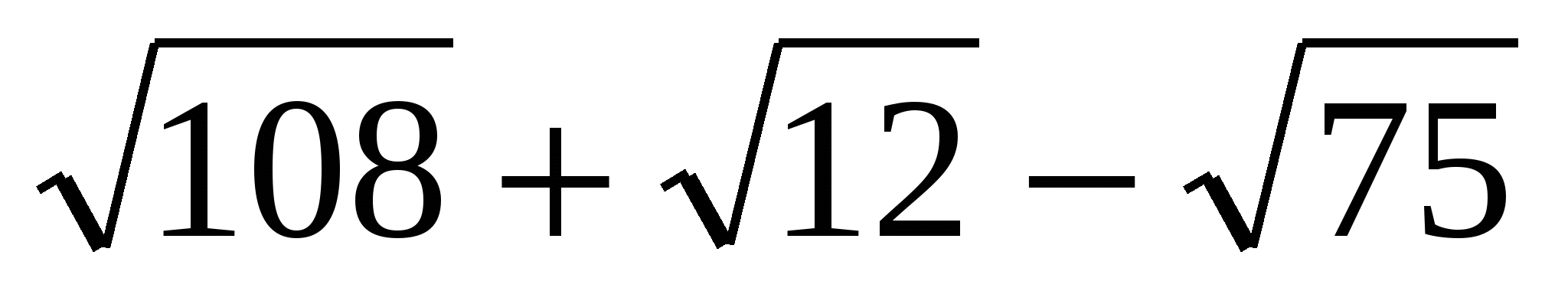 .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
-
Определите угловой коэффициент прямой
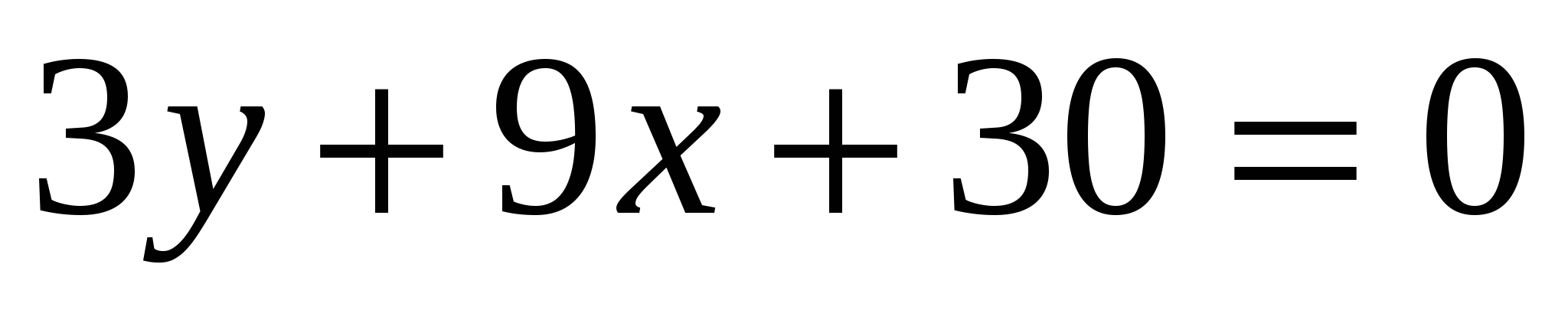 .
.
1) –3 2) ![]() 3) 3 4)
3) 3 4)![]()
-
Предел функции
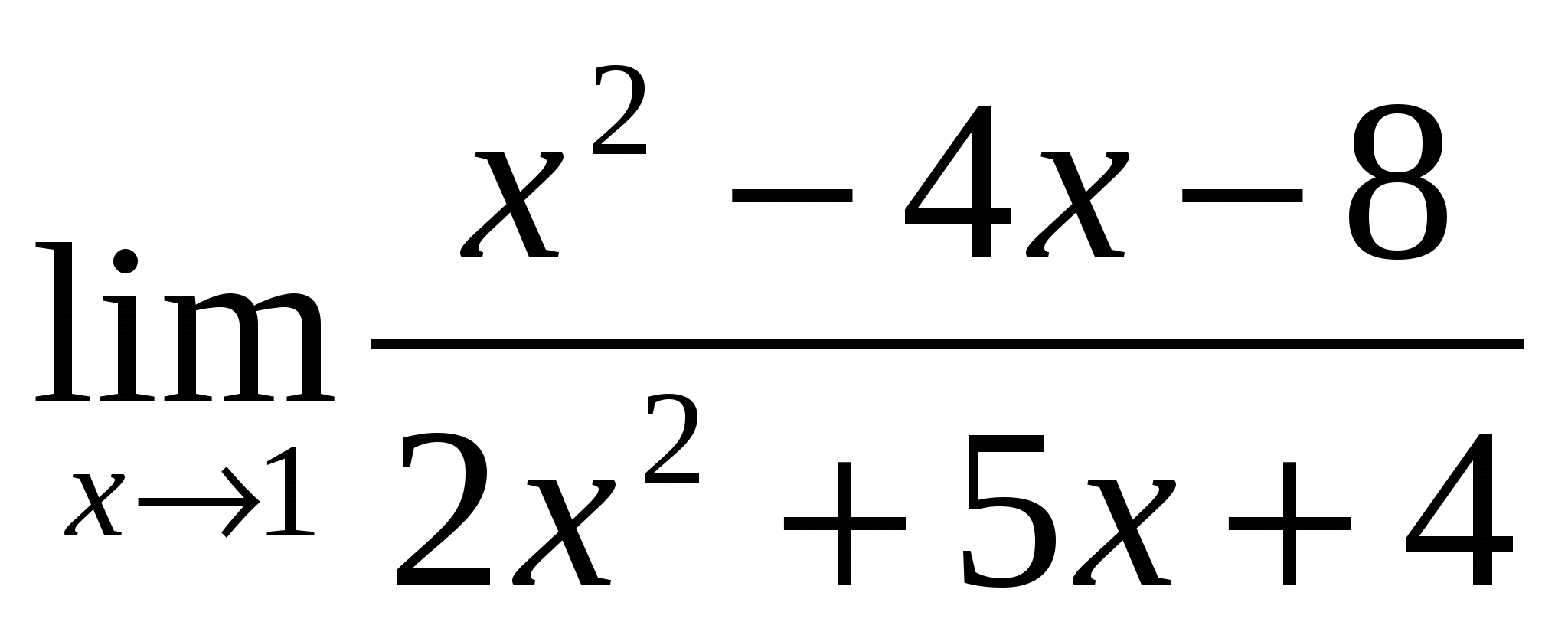 равен:
равен:
1) –2 2) –1 3) 0 4) ![]()
-
Объем первого цилиндра равен 5 см3. Найдите объем второго цилиндра, если при равных диаметрах, его высота в четыре раза больше, чем у первого.
1) 2,5 2) 25 3) 40 4) 20
-
Площадь полной поверхности куба равна 0,54 см2. Найдите длину ребра.
1) 0,6 2) 0,3 3) 0,9 4) 0,15
-
Общее количество ребер у октаэдра равно
1) 14 2) 16 3) 12 4) 10
-
Число сочетаний 4 элементов по 3 равно
1) 4 2) 3 3) 2 4) 7
При выполнении задания 12 – 16 укажите сначала номер задания, а затем запишите его решение.
-
Вычислите значение производной заданной функции при указанном значении независимой переменной:
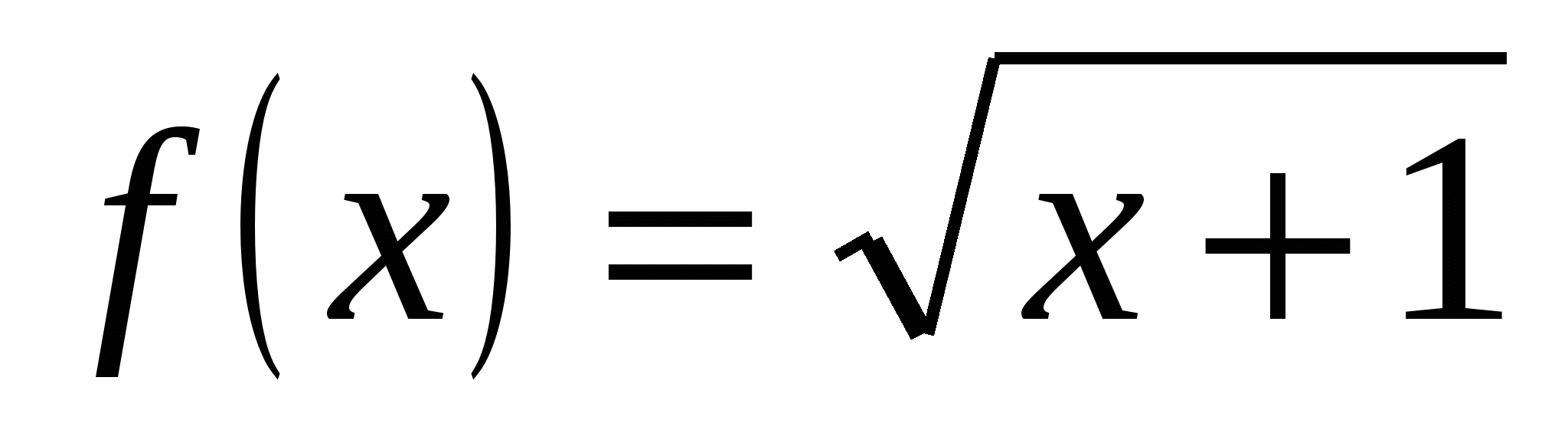 ;
; 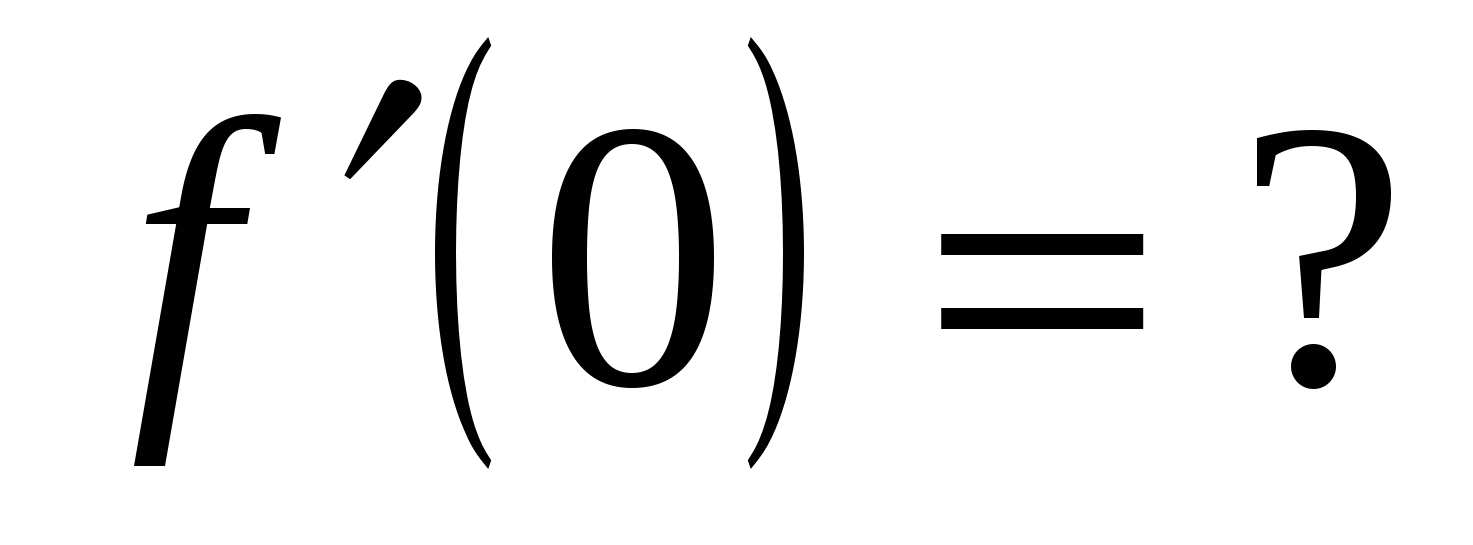
-
Найдите промежутки монотонности для функции
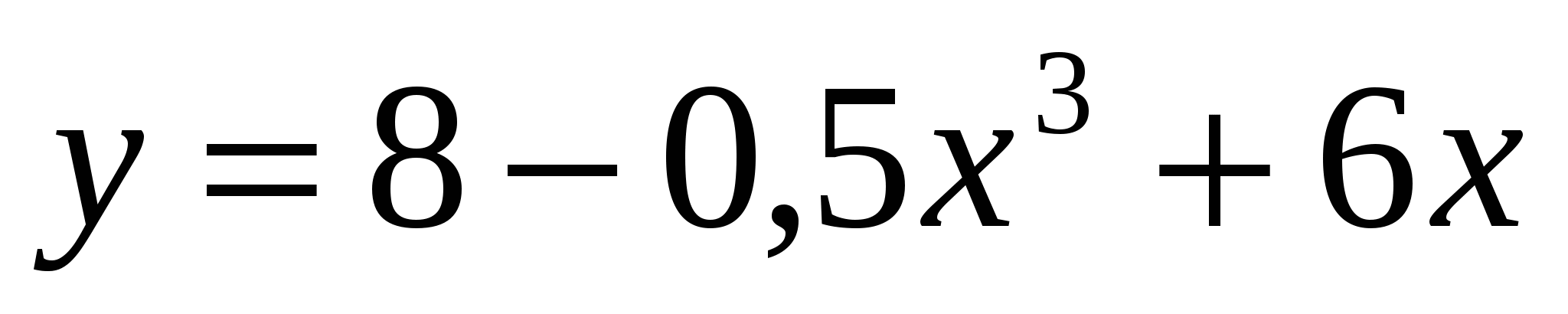 .
. -
Вычислите площадь фигуры, ограниченной заданными линиями
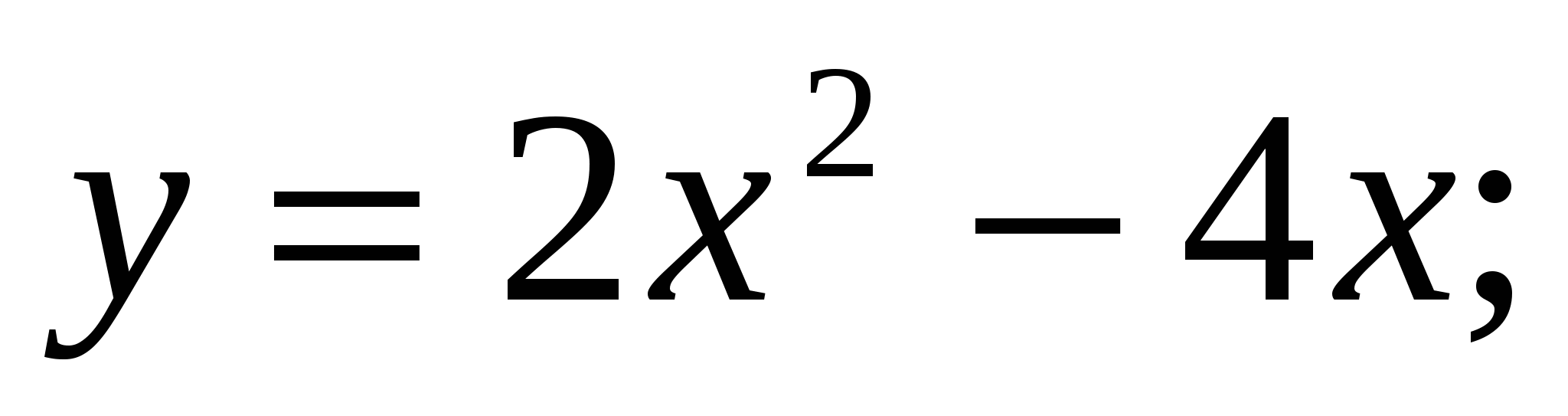
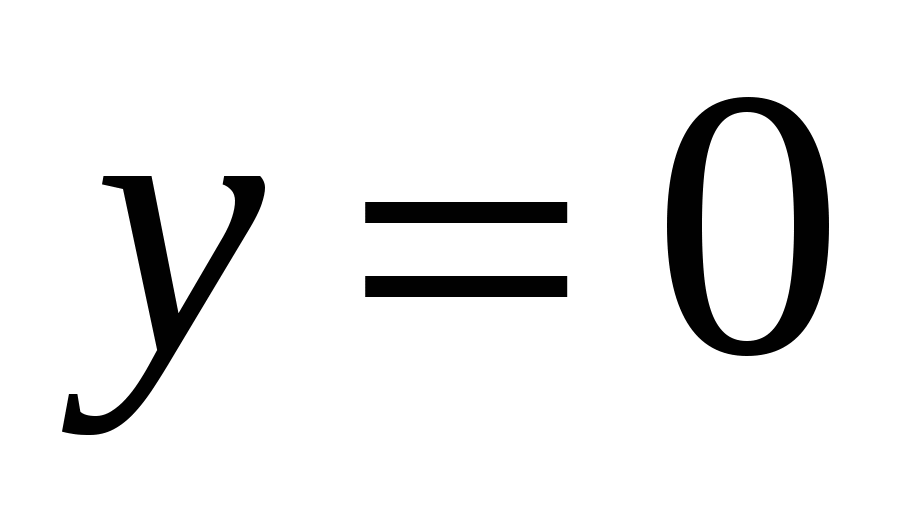 .
. -
Найдите значение выражения
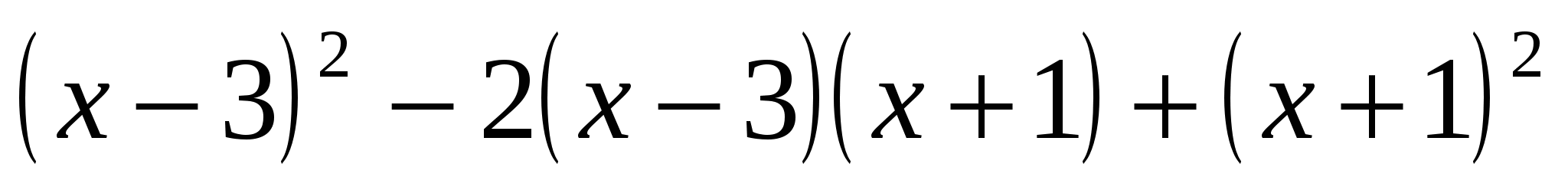 , при
, при 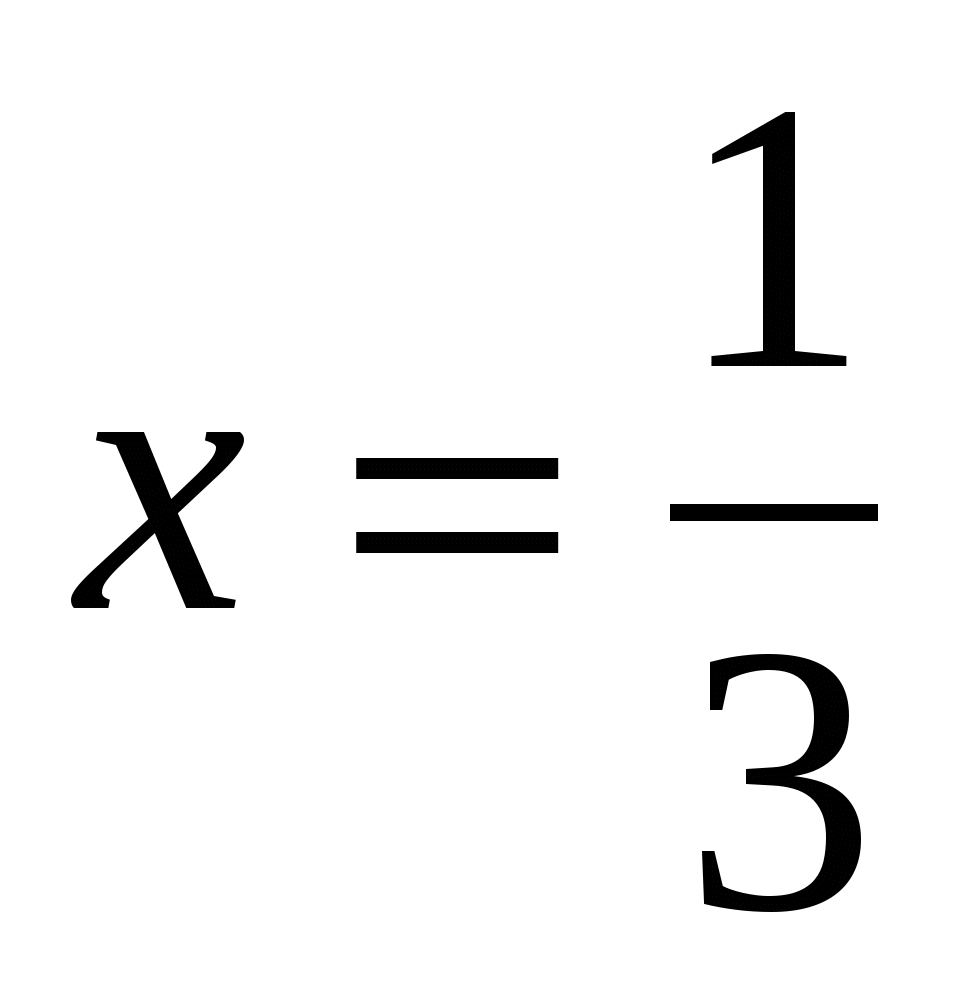 .
. -
Решите систему линейных уравнений методом Крамера:
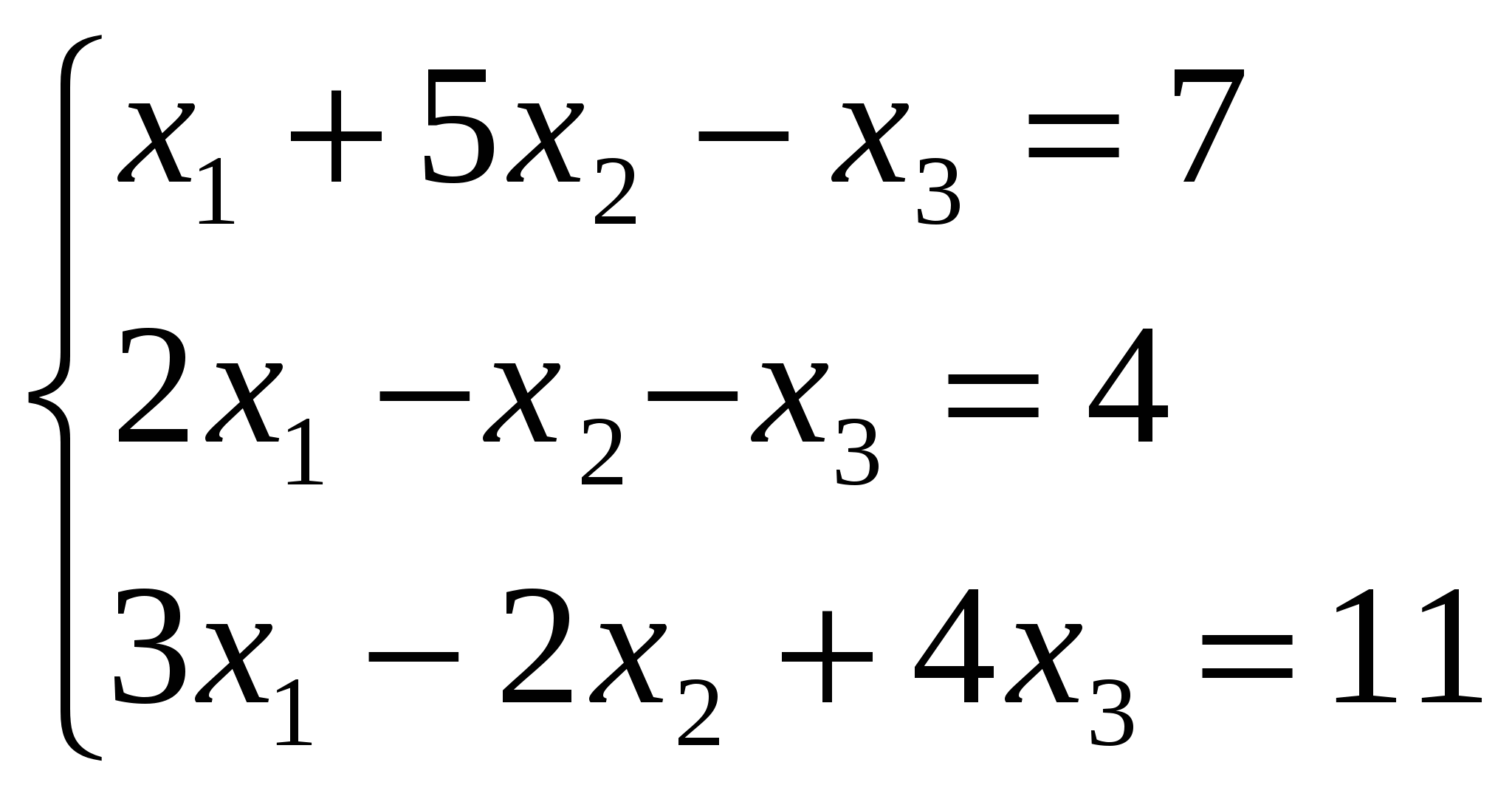
Вариант 9
При выполнении задания 1 – 11 в бланках ответа под номером соответствующего задания, поставьте номер правильного ответа.
-
Какое из указанных чисел является значением выражения
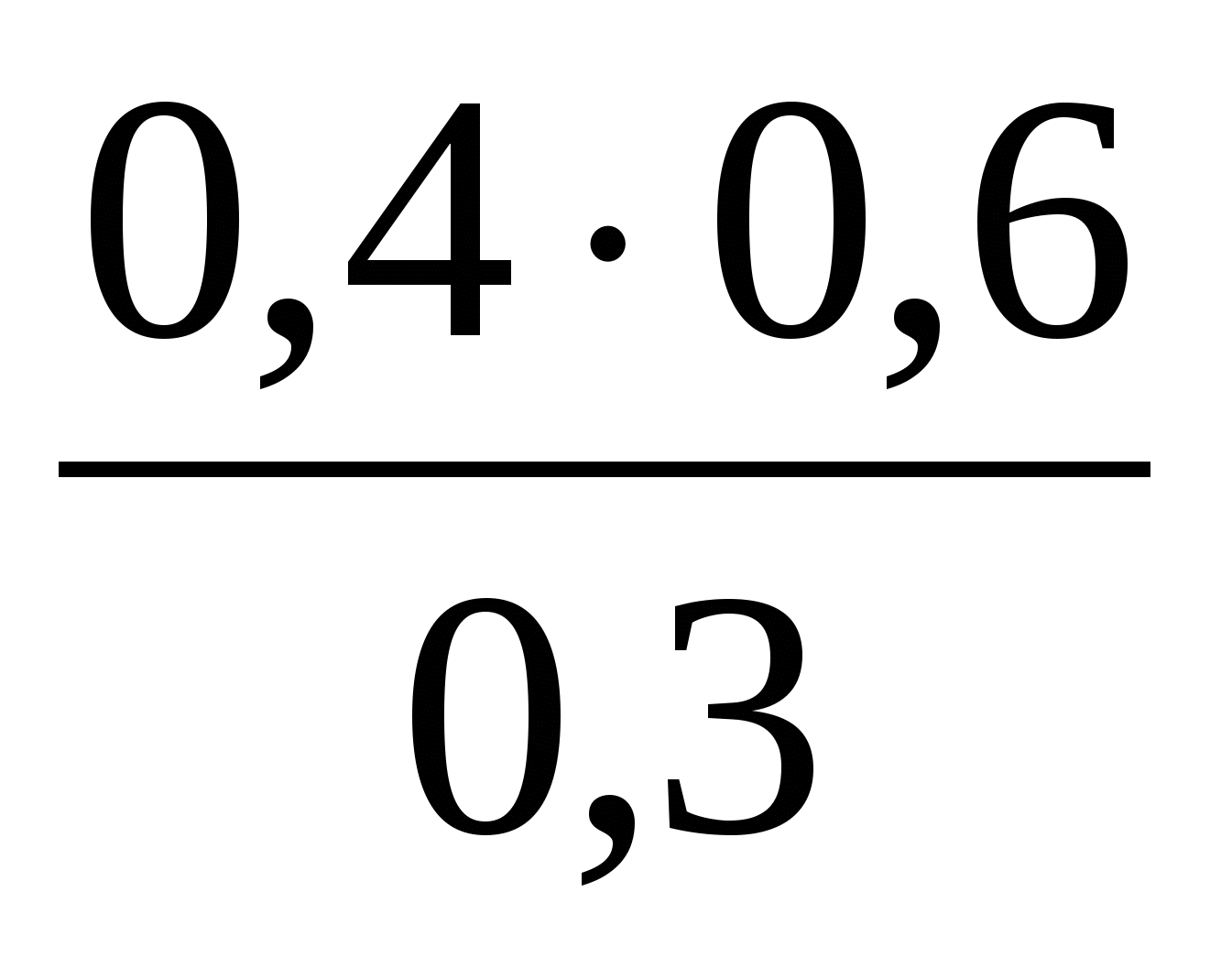 ?
?
1) 1,6 2) 0,5 3) 0,8 4) 8
-
Билет в кино стоит 350 рублей. Какое максимальное число билетов можно купить на 1500 рублей после повышения цены на 25%?
1) 4 2) 3 3) 5 4) 7
-
Найдите сtg
 , если tg
, если tg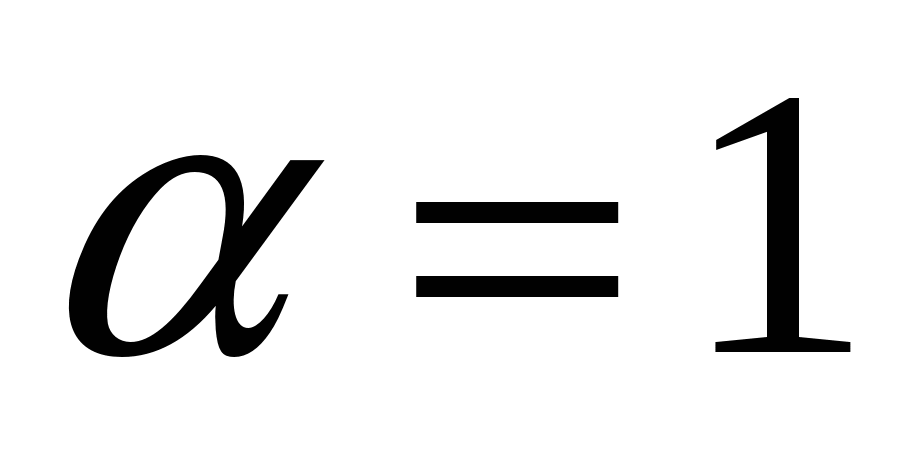 ,
, 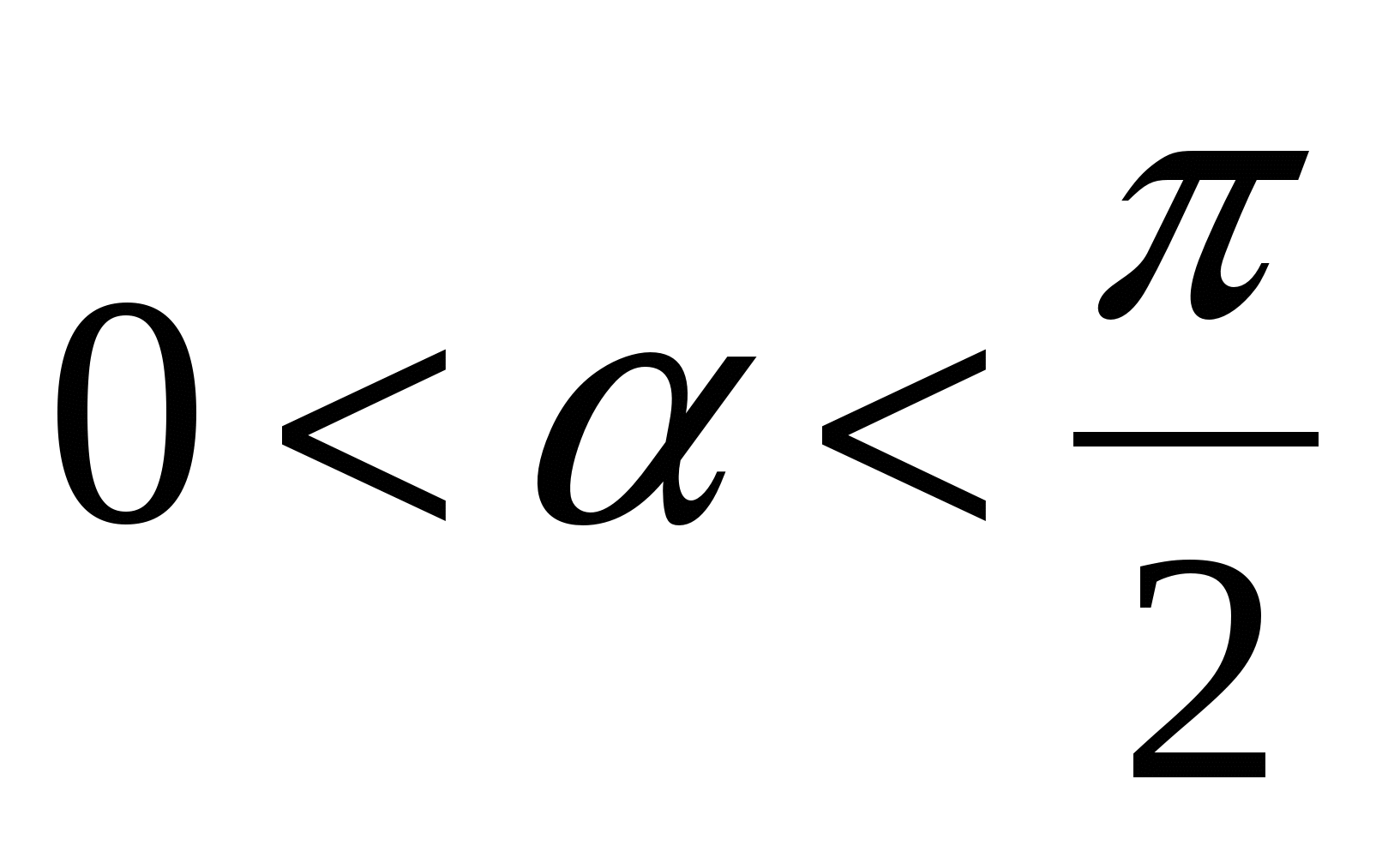 ..
..
1) ![]() 2) 0 3)
2) 0 3) ![]() 4) 1
4) 1
-
В сборнике по географии всего 40 билетов, в восьми из них встречается вопрос о морях. На экзамене школьнику достается один случайно выбранный билет из этого сборника. Какова вероятность того, что в этом билете будет вопрос о морях?
1) 0,2 2) 0,8 3) 0,5 4) 5
-
Упростите выражение и выберите правильный ответ
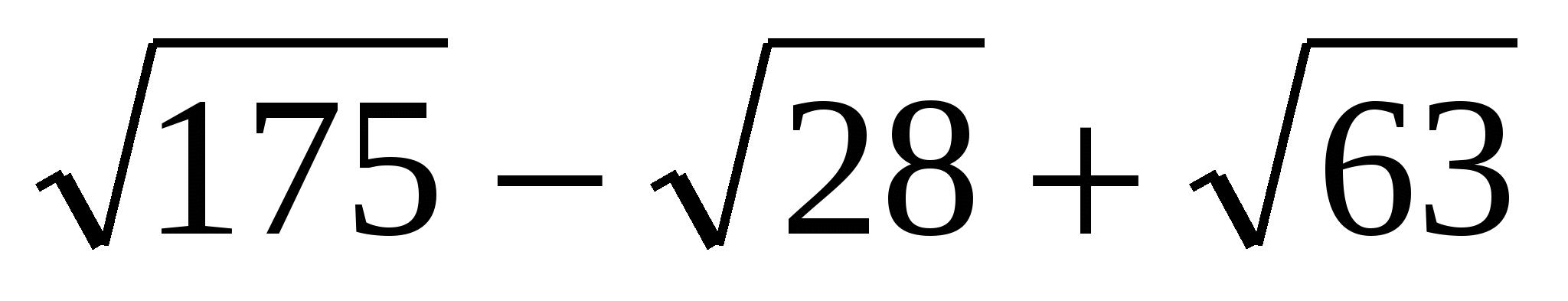 .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
-
Определите угловой коэффициент прямой
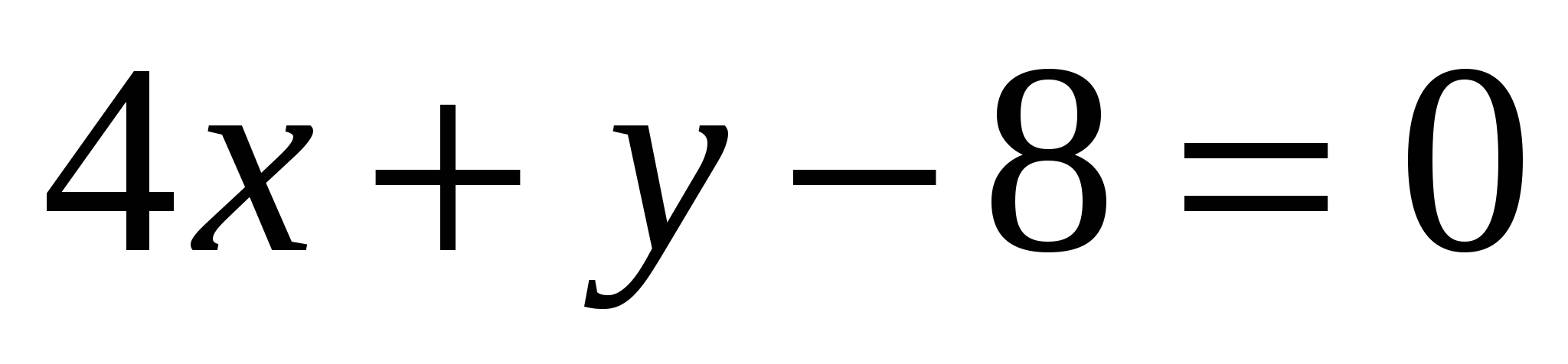 .
.
1) – 4 2) ![]() 3) 4 4)
3) 4 4)![]()
-
Предел функции
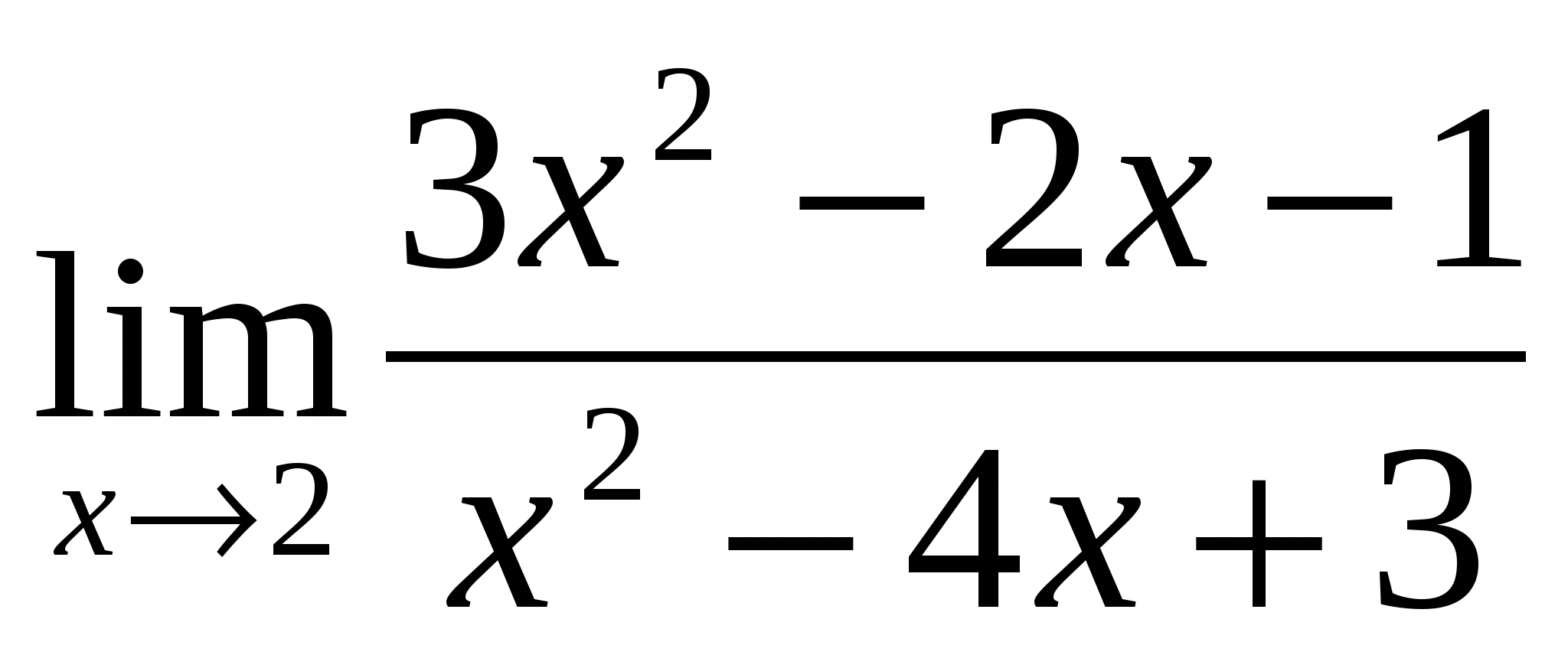 равен:
равен:
1) – 7 2) 7 3) ![]() 4)
4) ![]()
-
Объем первого цилиндра равен 6 см3. Найдите объем второго цилиндра, если при равных диаметрах, его высота в два раза больше, чем у первого.
1) 2 2) 12 3) 36 4) 24
-
Площадь полной поверхности куба равна 0,96 см2. Найдите длину ребра.
1) 0,6 2) 0,3 3) 0,9 4) 0,4
-
Общее количество граней у додекаэдра равно
1) 30 2) 20 3) 25 4) 18
-
Число сочетаний 7 элементов по 5 равно
1) 22 2) 35 3) 21 4) 36
При выполнении задания 12 – 16 укажите сначала номер задания, а затем запишите его решение.
-
Вычислите значение производной заданной функции при указанном значении независимой переменной:
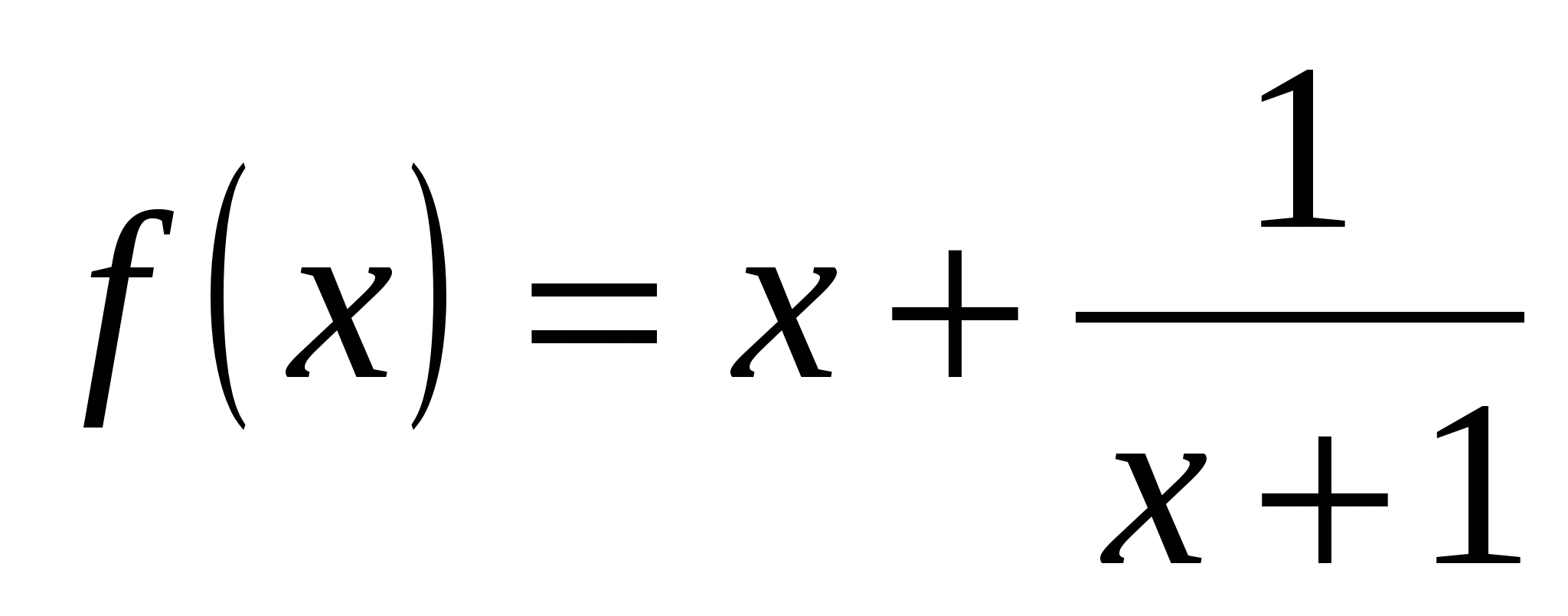 ;
; 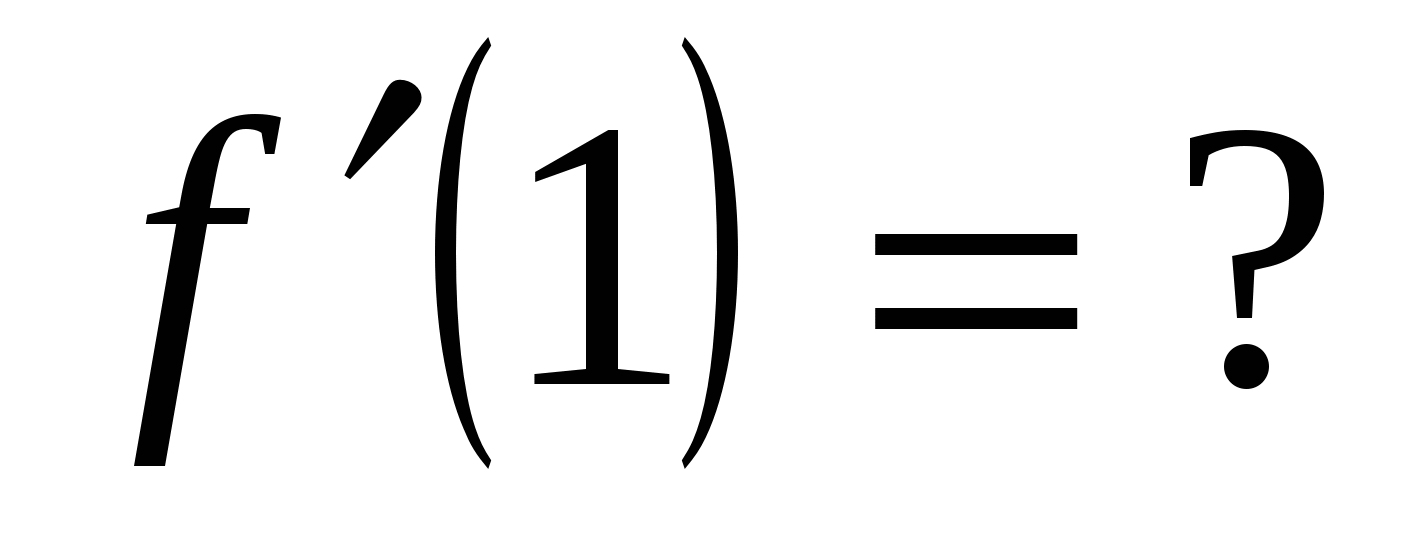
-
Найдите промежутки монотонности для функции
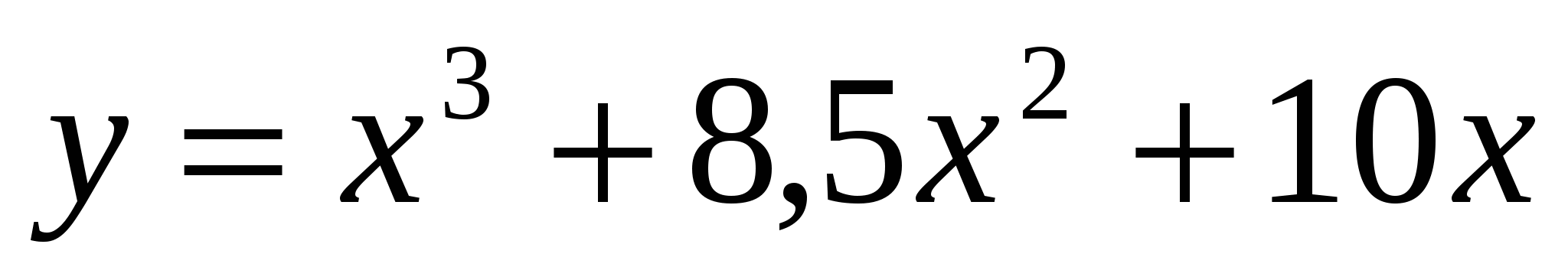 .
. -
Вычислите площадь фигуры, ограниченной заданными линиями
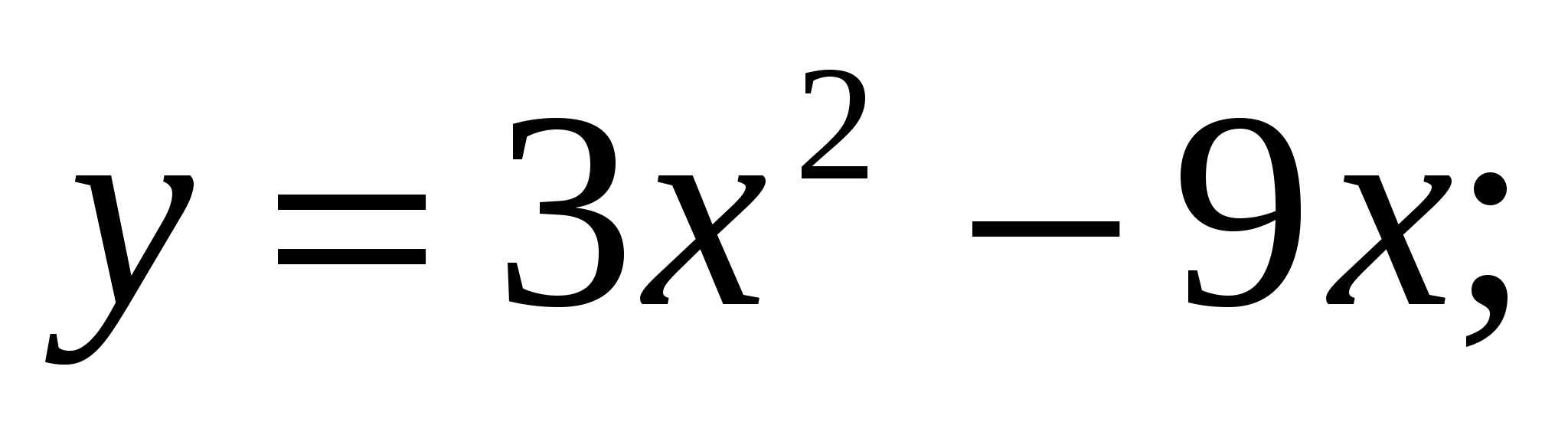
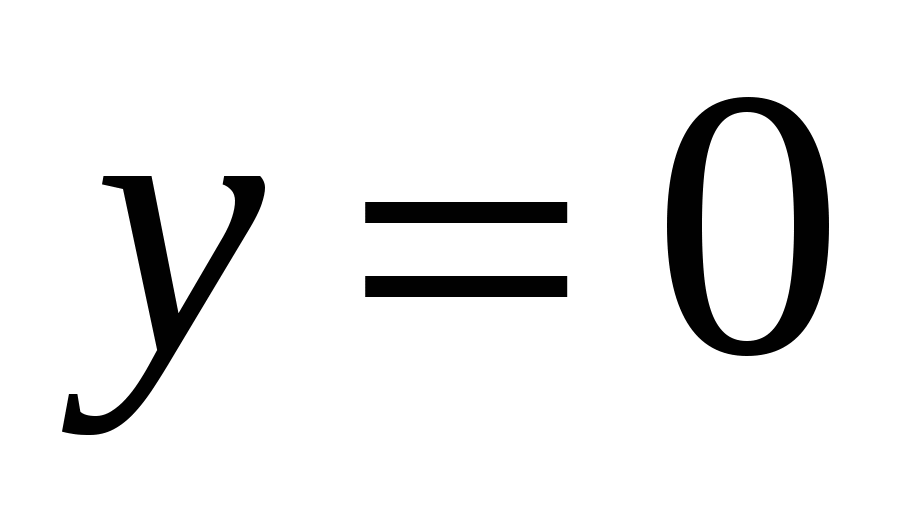 .
. -
Найдите значение выражения
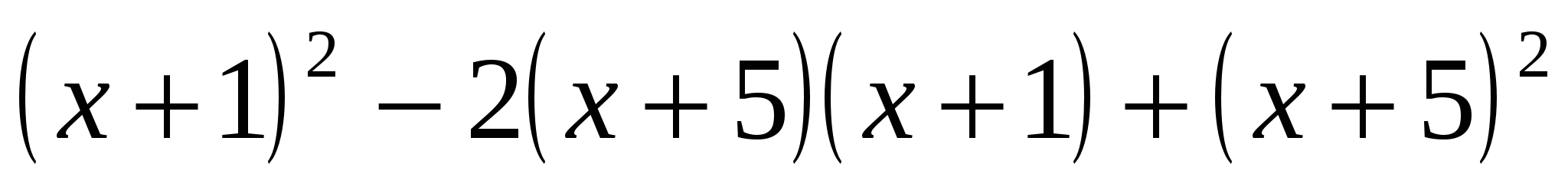 , при
, при 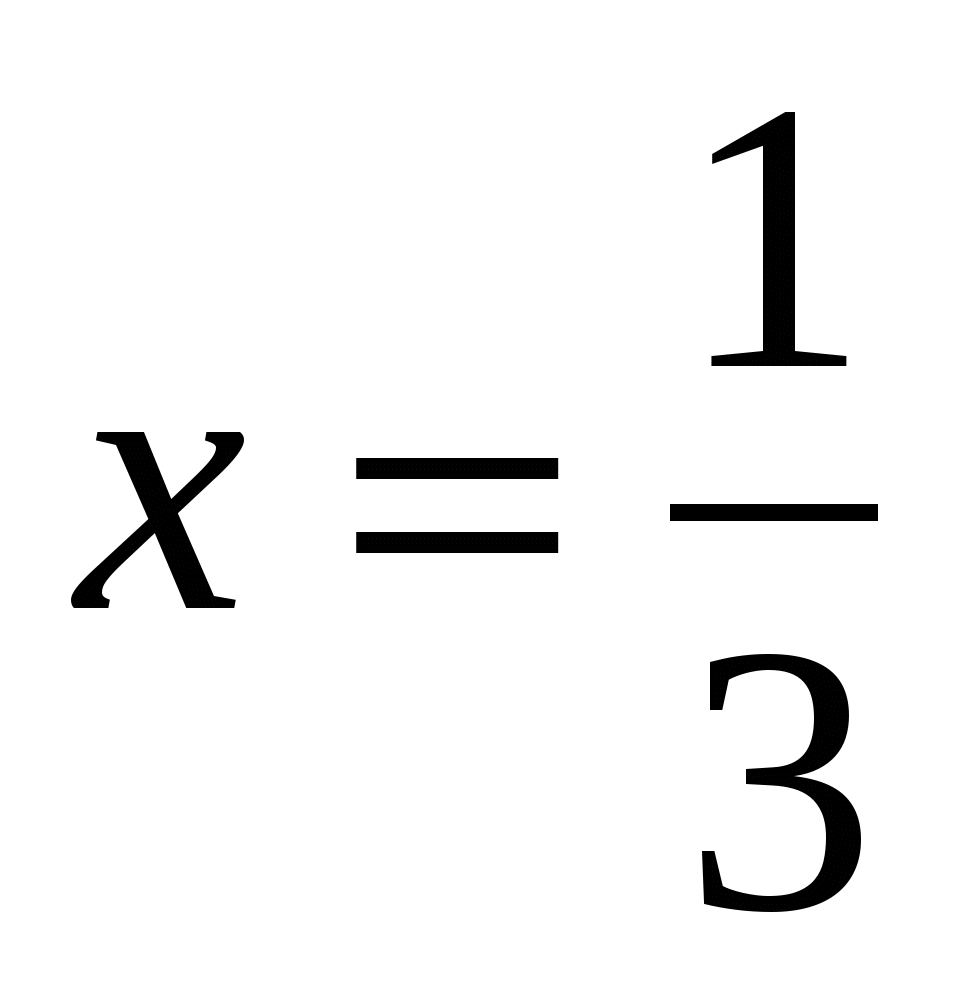 .
. -
Решите систему линейных уравнений методом Крамера:
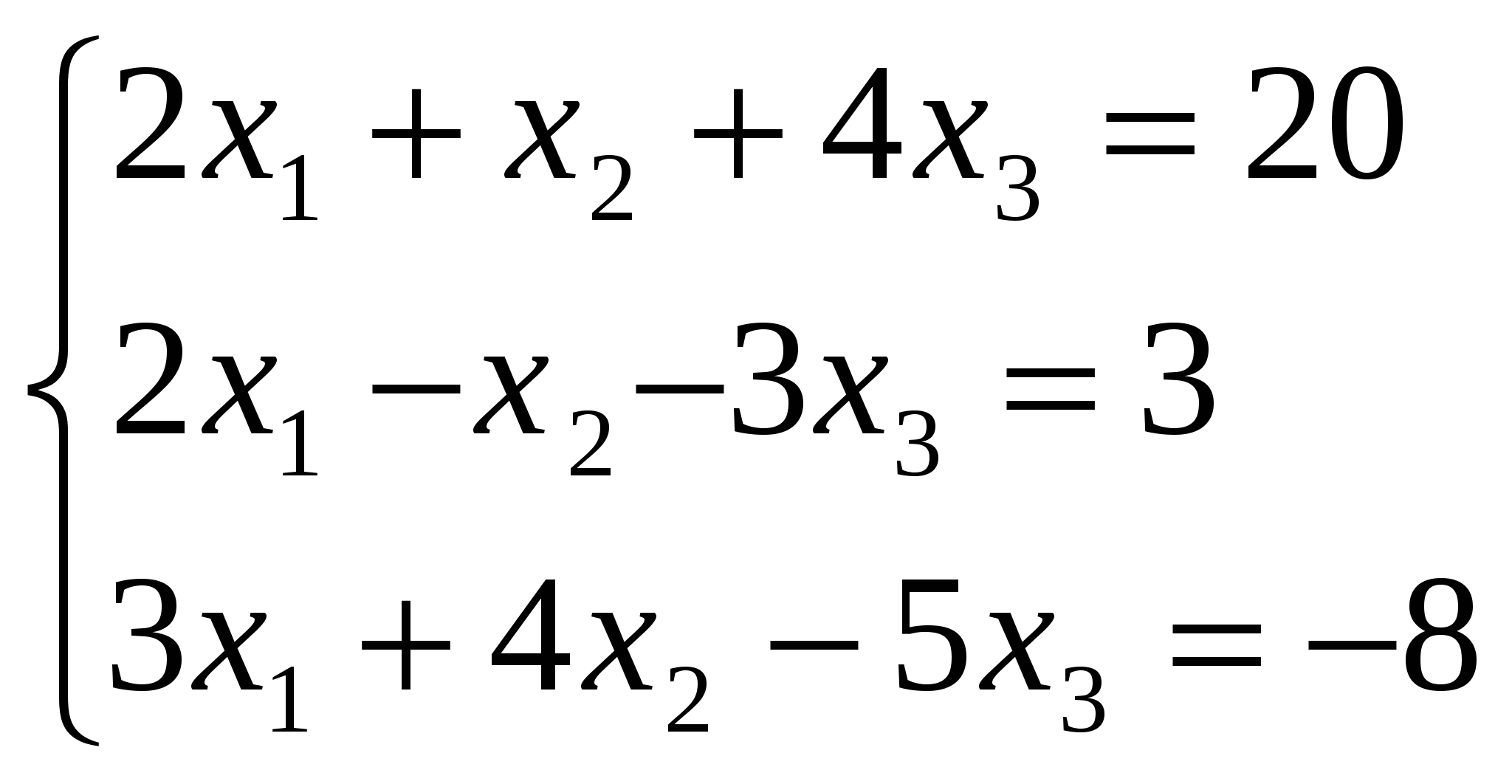
Вариант 10
При выполнении задания 1 – 11 в бланках ответа под номером соответствующего задания, поставьте номер правильного ответа.
-
Какое из указанных чисел является значением выражения
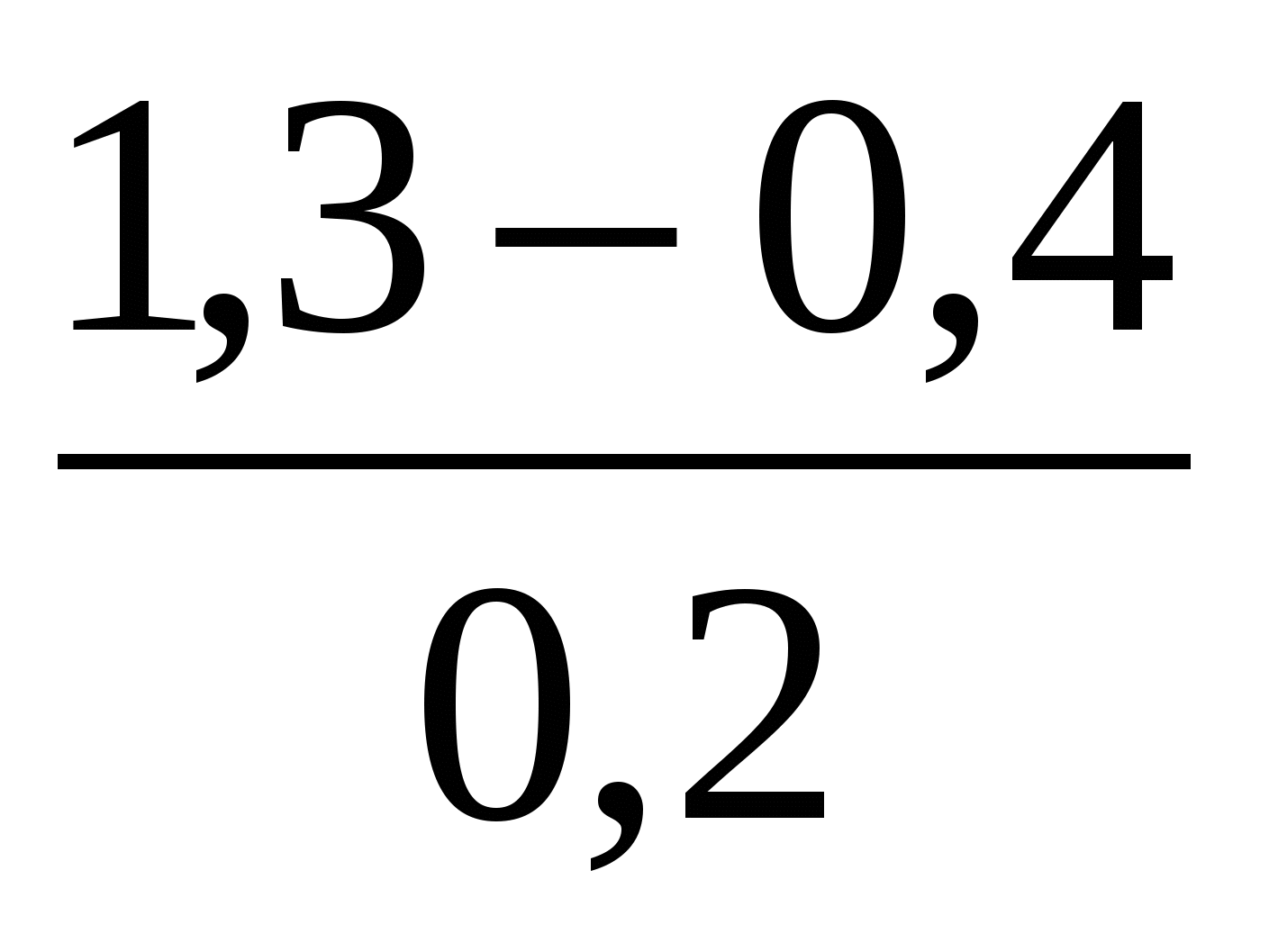 ?
?
1) 0,45 2) 4,5 3) 0,2 4) 2
-
Билет в театр стоит 125 рублей. Какое максимальное число билетов можно купить на 1500 рублей после повышения цены на 15%?
1) 9 2) 12 3) 10 4) 11
-
Найдите
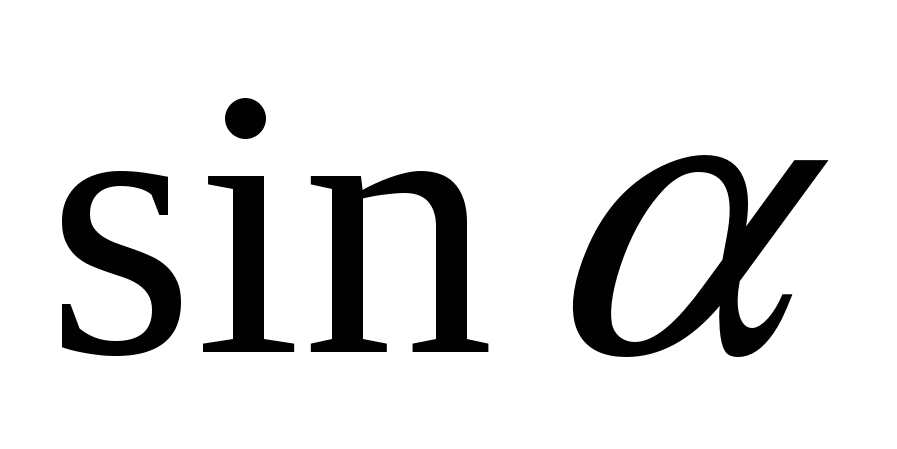 , если
, если 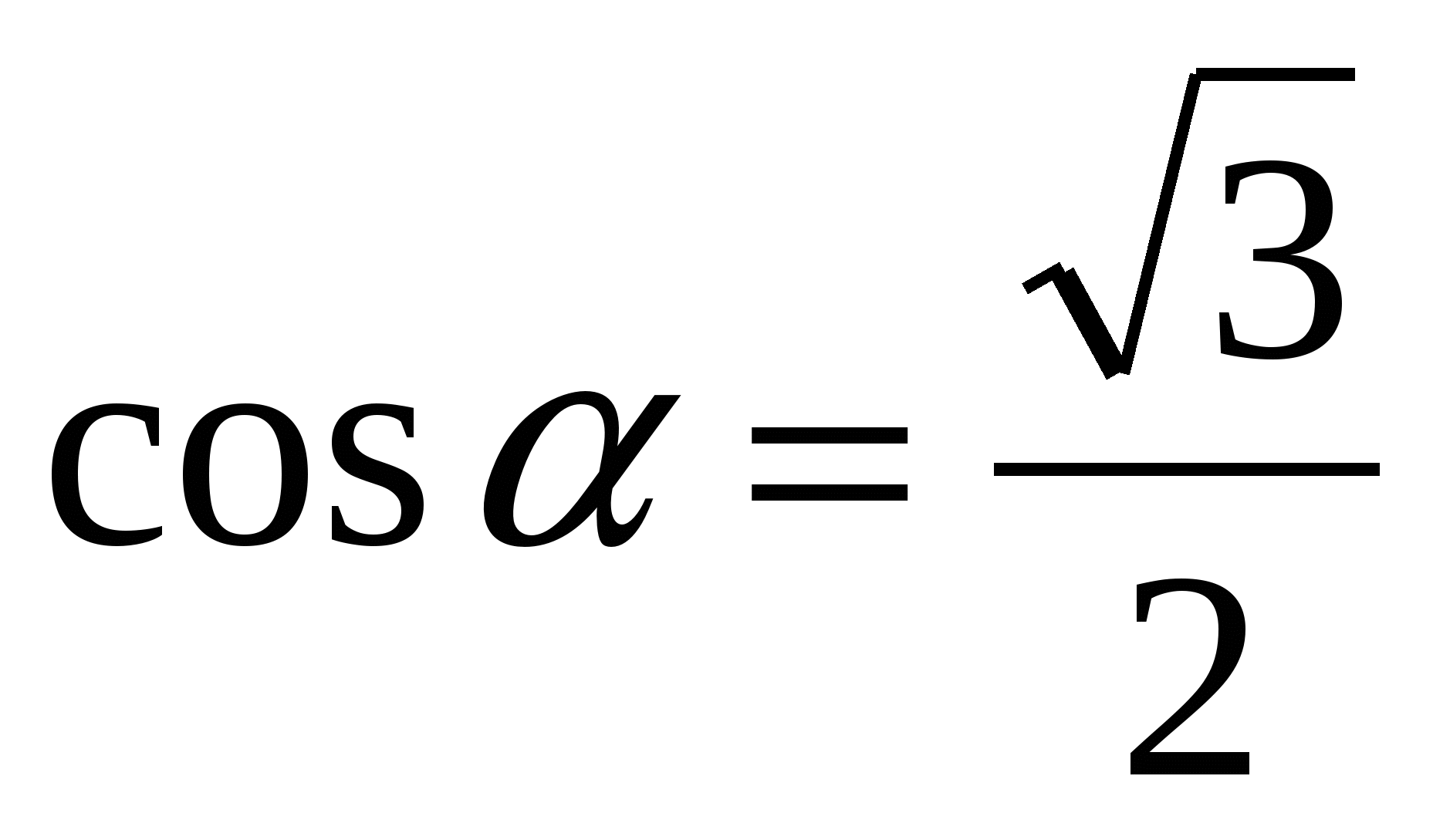 ,
, 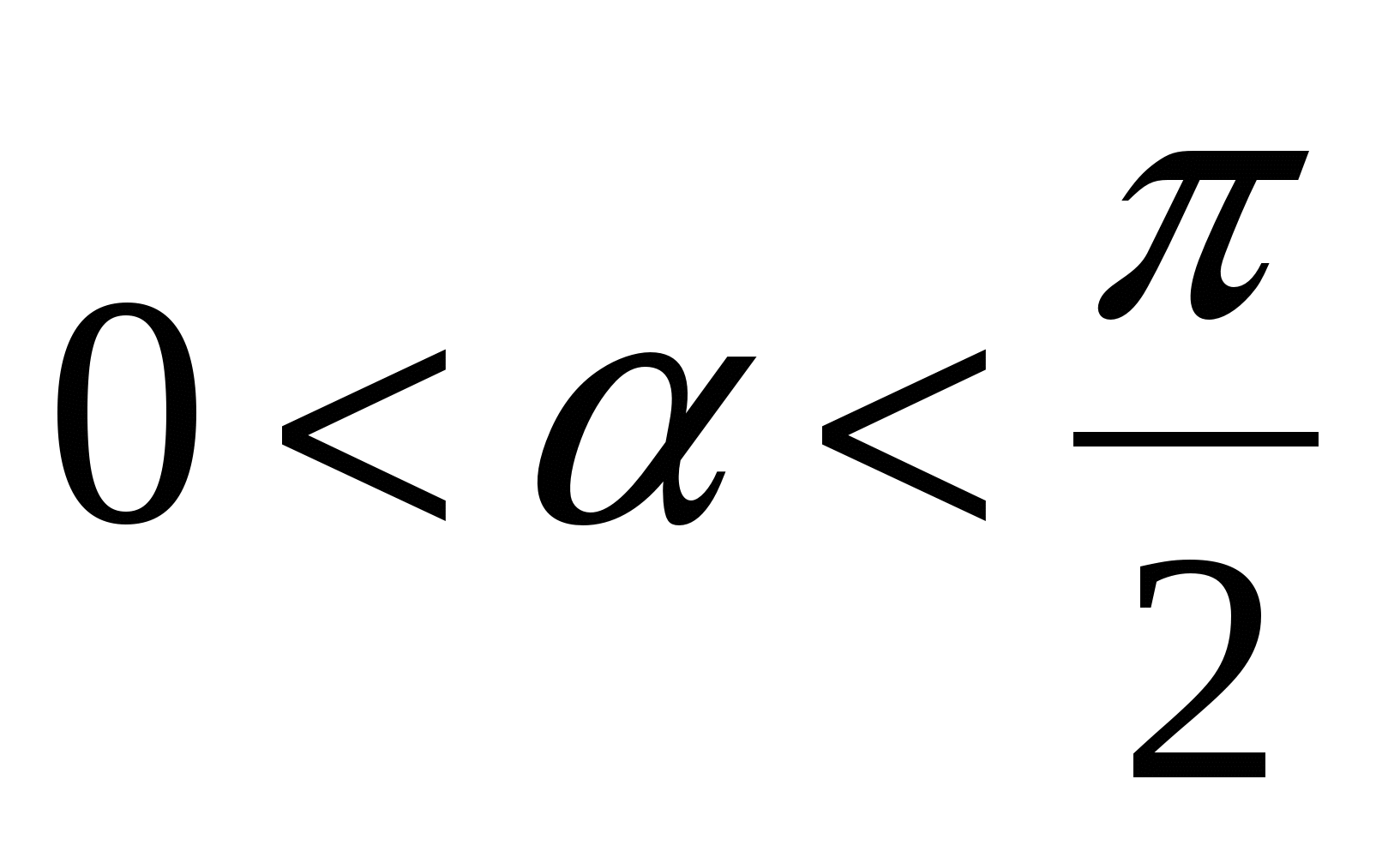 .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4) 1
4) 1
-
В сборнике по физике всего 24 билета, в шести из них встречаются вопросы о силе тяжести. На экзамене школьнику достается один случайно выбранный билет из этого сборника. Какова вероятность того, что в этом билете будет вопрос о силе тяжести?
1) 0,5 2) 0,75 3) 0,25 4) 0,3
-
Упростите выражение и выберите правильный ответ
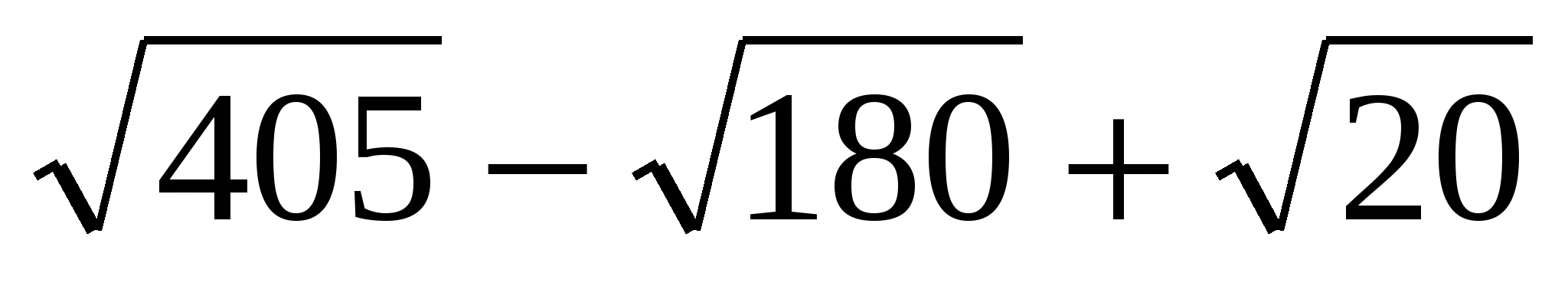 .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
-
Определите угловой коэффициент прямой
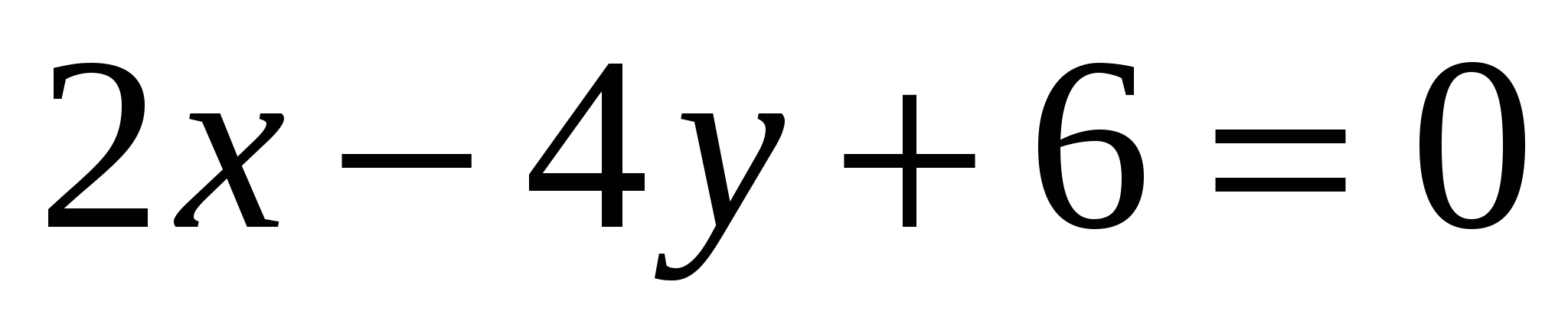 .
.
1) – 2 2) ![]() 3) 2 4)
3) 2 4)![]()
-
Предел функции
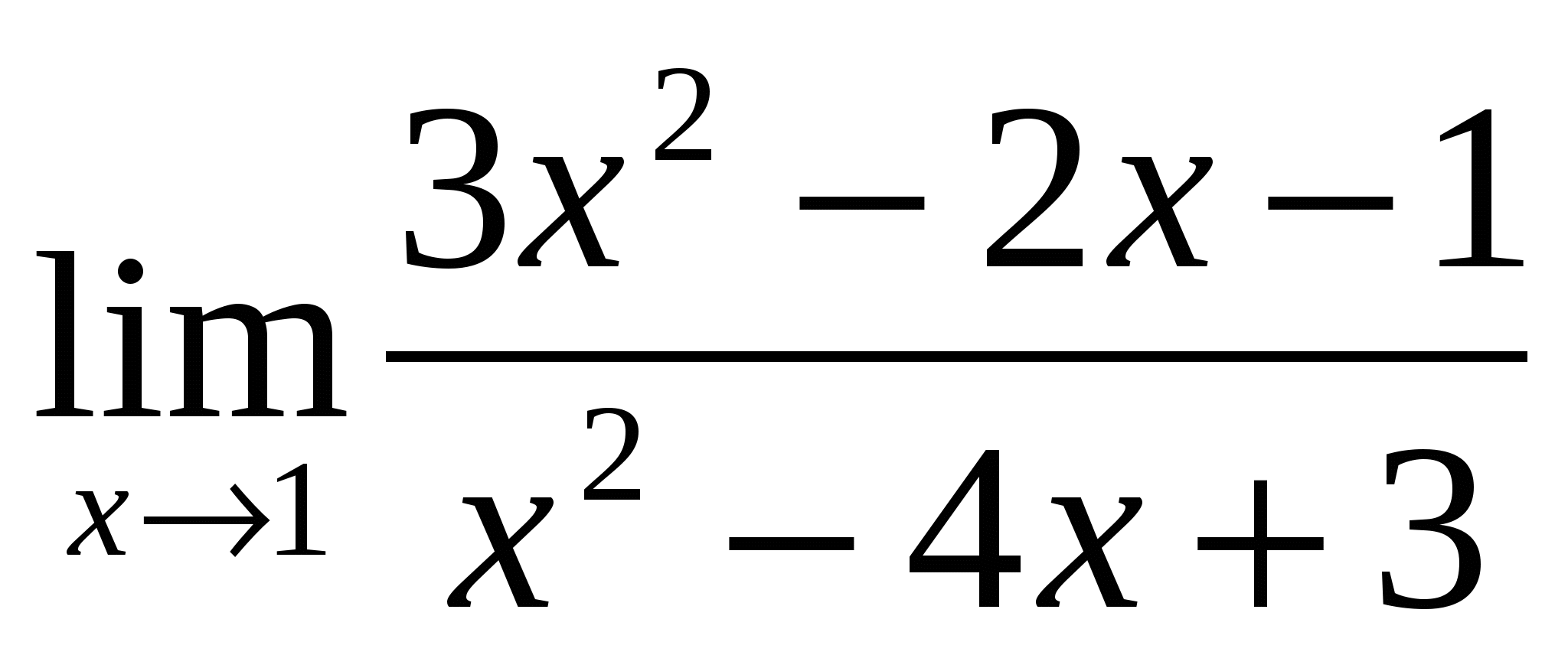 равен:
равен:
1) – 2 2) 2 3) 0 4) ![]()
-
Объем первого цилиндра равен 4 см3. Найдите объем второго цилиндра, если при равных диаметрах, его высота в четыре раза больше, чем у первого.
1) 4 2) 16 3) 8 4) 20
-
Площадь полной поверхности куба равна 1,5 см2. Найдите длину ребра.
1) 0,75 2) 0,5 3) 0,3 4) 0,25
-
Общее количество вершин у додекаэдра равно
1) 24 2) 26 3) 20 4) 22
-
Число сочетаний 7 элементов по 3 равно
1) 25 2) 35 3) 45 4) 55
При выполнении задания 12 – 16 укажите сначала номер задания, а затем запишите его решение.
-
Вычислите значение производной заданной функции при указанном значении независимой переменной:
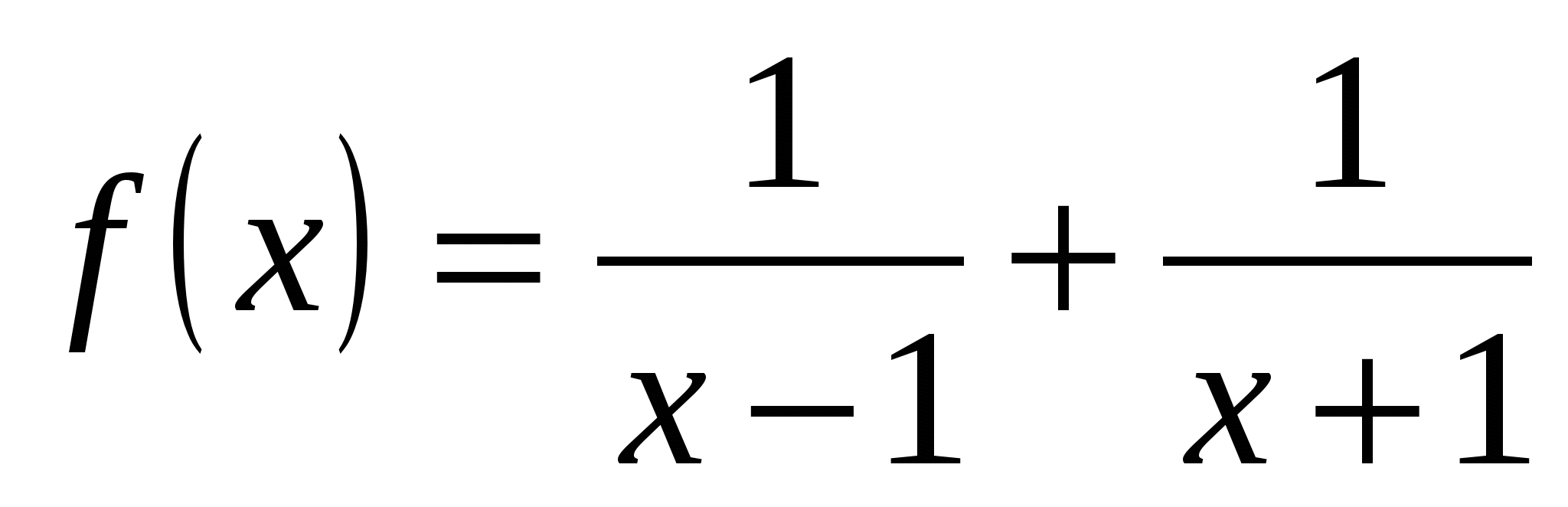 ;
; 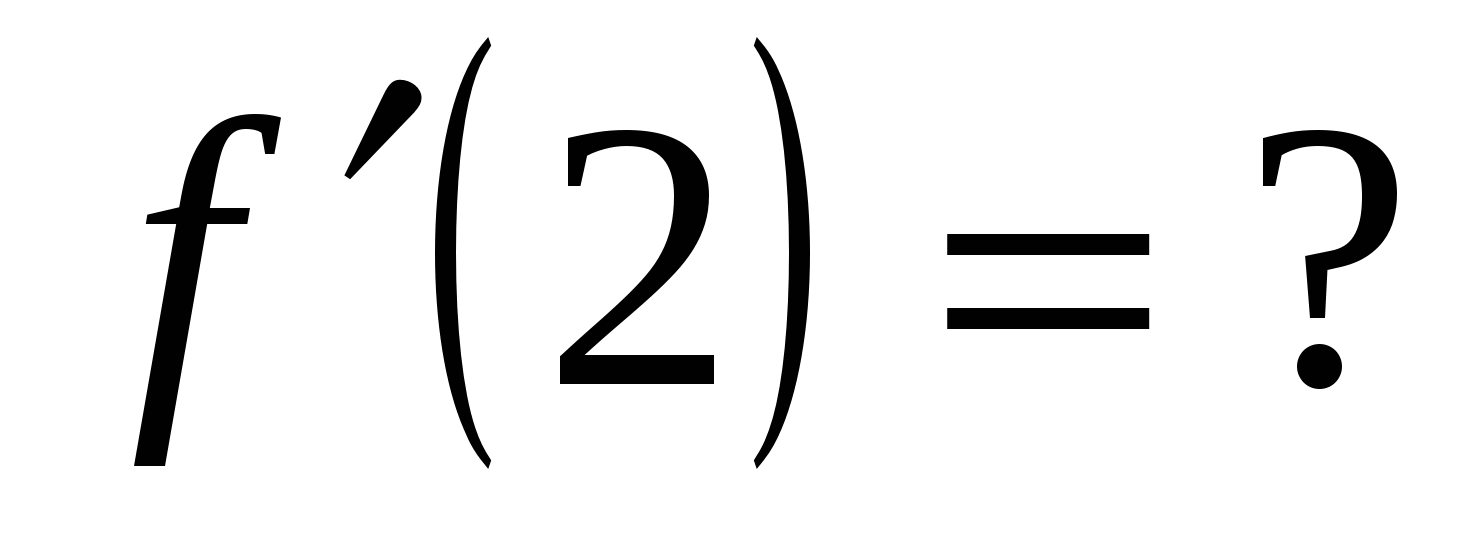
-
Найдите промежутки монотонности для функции
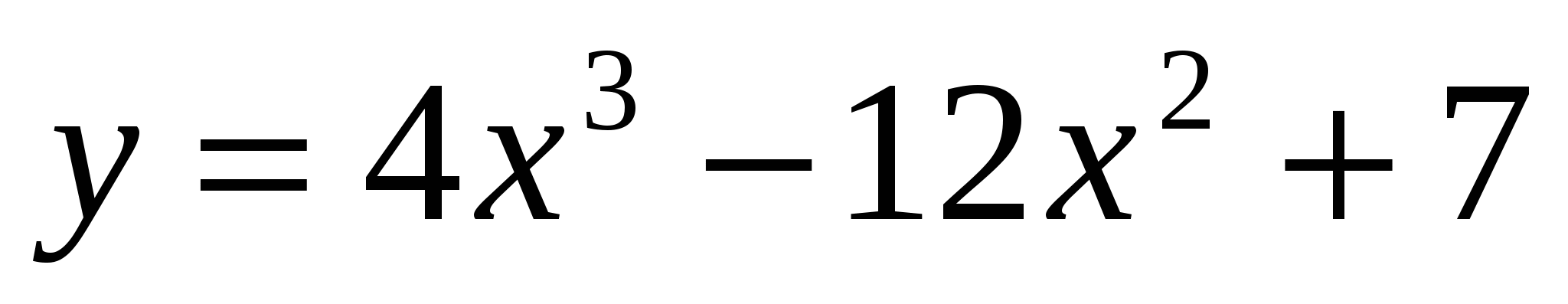 .
. -
Вычислите площадь фигуры, ограниченной заданными линиями
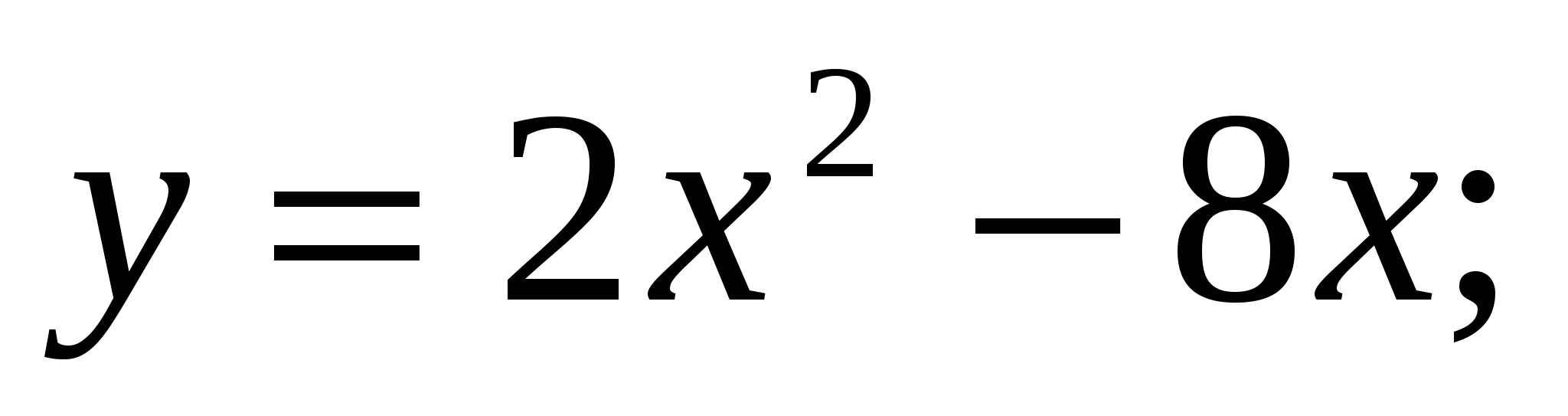
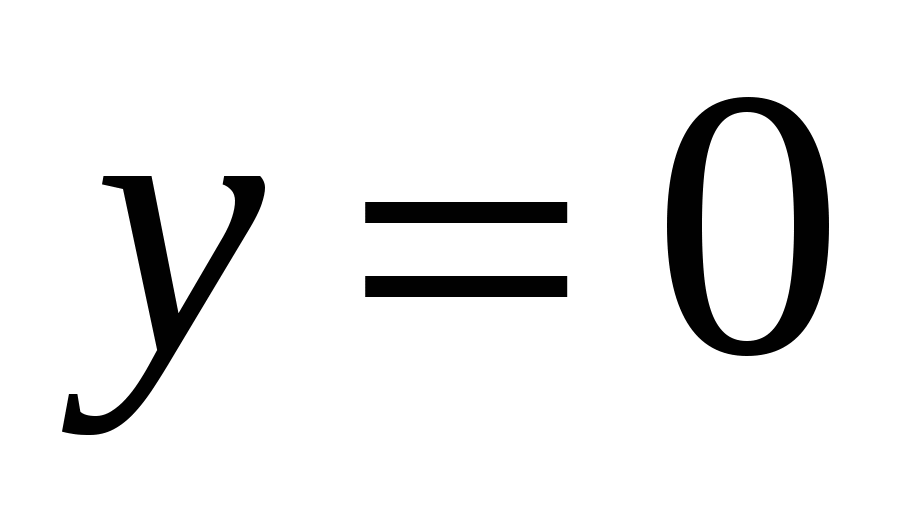 .
. -
Найдите значение выражения
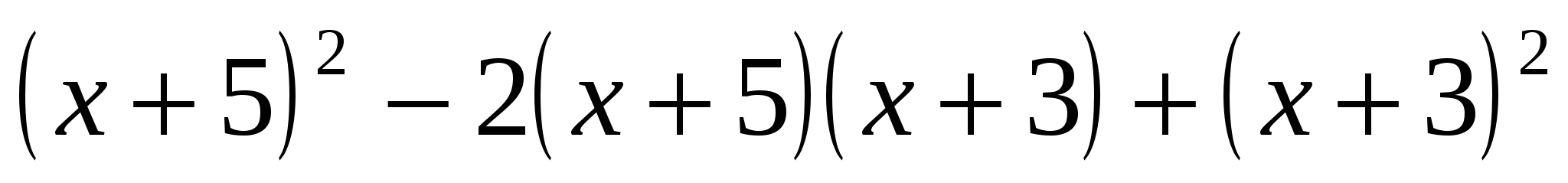 , при
, при 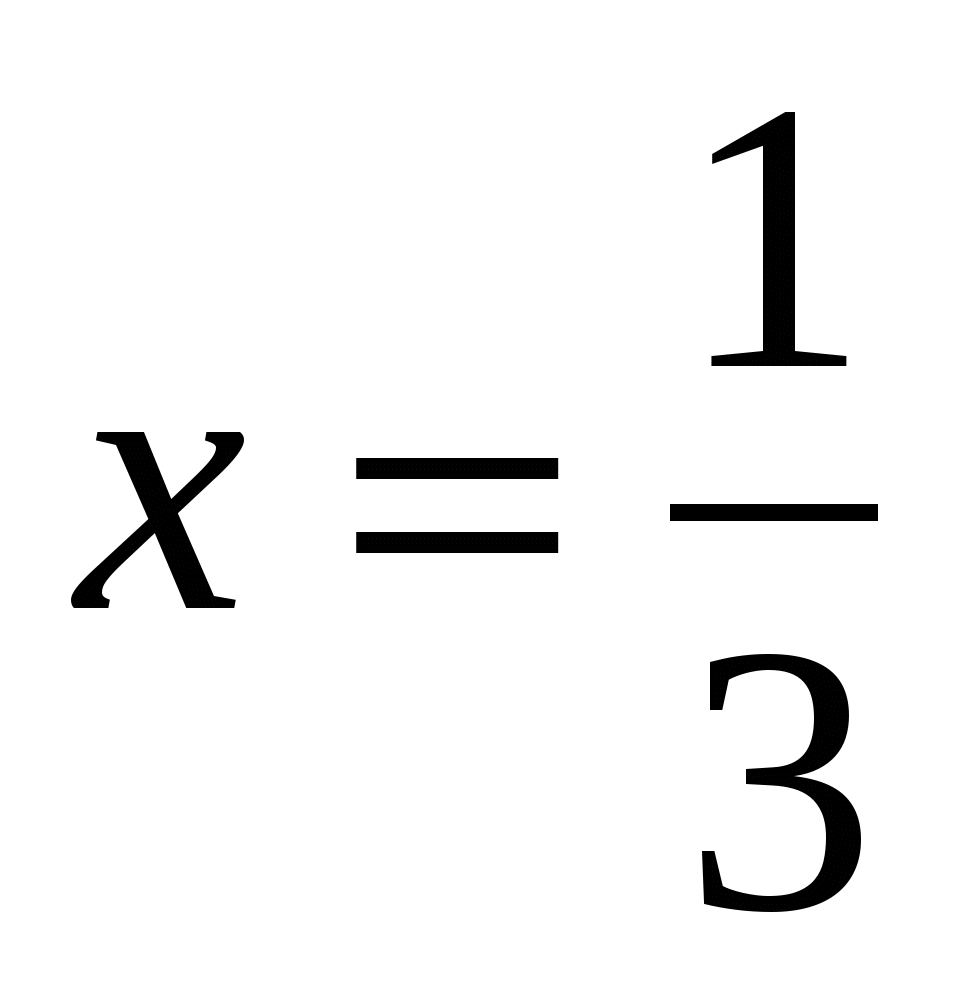 .
. -
Решите систему линейных уравнений методом Крамера:
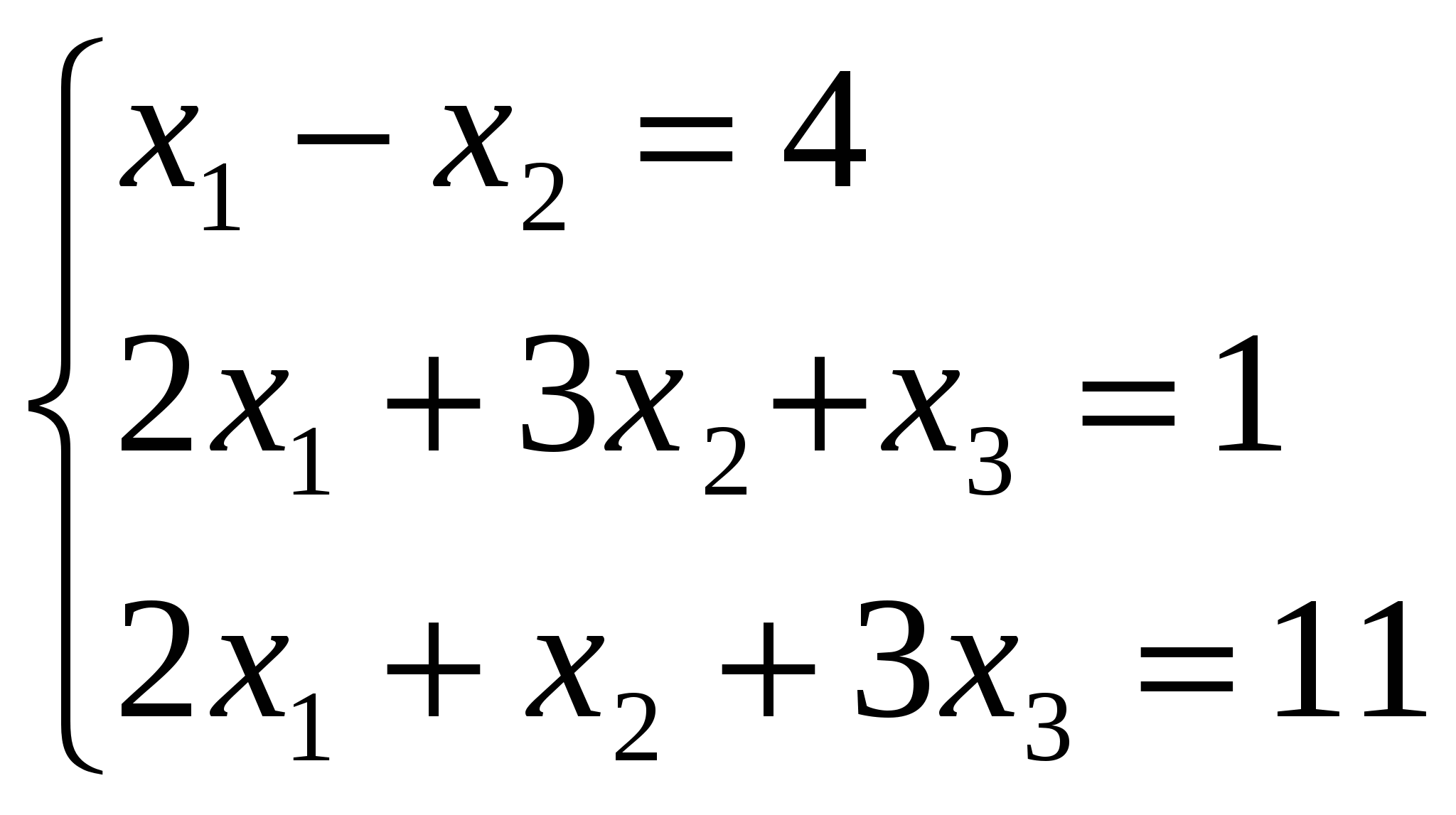
Здесь представлены материалы теста на тему «КОМПЛЕКТ ЭКЗАМЕНАЦИОННЫХ ТЕСТОВ ПО МАТЕМАТИКЕ (для студентов 1 курса дневного отделения)», которые могут быть просмотрены в онлайн режиме или же их можно бесплатно скачать. Предмет теста: Математика (все классы). Также здесь Вы найдете подборку тестов на схожие темы, что поможет в еще лучшей подготовке к тестированию.

