Олимпиадные задания по математике для учащихся 8-ых классов
Олимпиадные задания по математике
для учащихся 8-ых классов
Куст Анжела Эдвардовна
учитель математики
МБОУ гимназии г. Гурьевска
Гурьевского района Калининградской области
Олимпиада по математике
8 класс
-
Запишите число 2000, используя восемь троек, скобки и арифметические операции. (7 баллов)
-
Каково наименьшее натуральное число
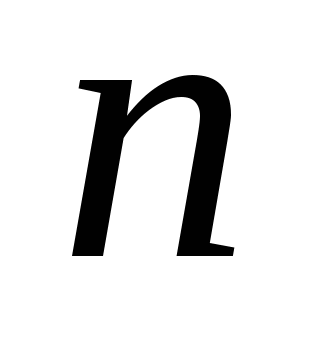 , такое, что
, такое, что 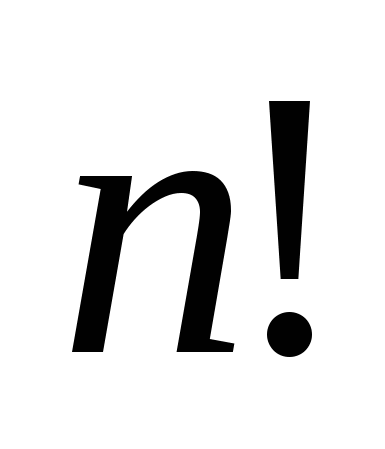
(где ![]() ) делится одновременно на 18, 19, 20 и 21? (7 баллов)
) делится одновременно на 18, 19, 20 и 21? (7 баллов)
-
Трёхзначное число
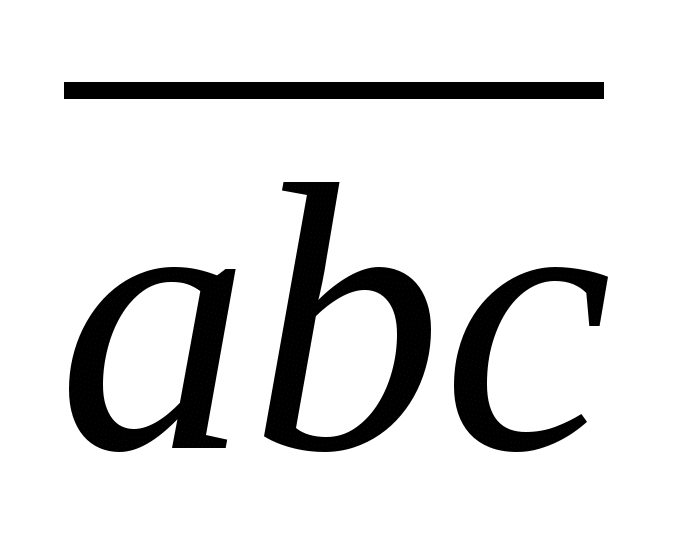 делится на 37. Докажите, что сумма чисел
делится на 37. Докажите, что сумма чисел
![]() и
и ![]() также делится на 37. (7 баллов)
также делится на 37. (7 баллов)
-
Какое наименьшее количество чисел нужно исключить из набора
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 так, чтобы оставшиеся числа можно было
разбить на две группы с одинаковым произведением чисел в группах?
Приведите пример такого разбиения на группы. (7 баллов)
-
На вопрос о возрасте его детей математик ответил: «У нас трое детей. Когда родился наш первенец, суммарный возраст членов семьи был равен 45 годам, год назад, когда родился третий ребёнок, – 70 лет, а в этом году суммарный возраст детей – 14 лет». Каков возраст детей математика? (7 баллов)
-
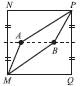
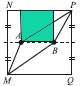
MNPQ – квадрат со стороной 6 см, А и В – две точки на его средней линии (средняя линия квадрата – отрезок, соединяющий середины двух его противоположных сторон). Ломанные МАР и МВР делят квадрат на 3 части одинаковой площади. Чему равна длина АВ? (7 баллов)
Ответы и решения
к олимпиадным задачам
-
Например:
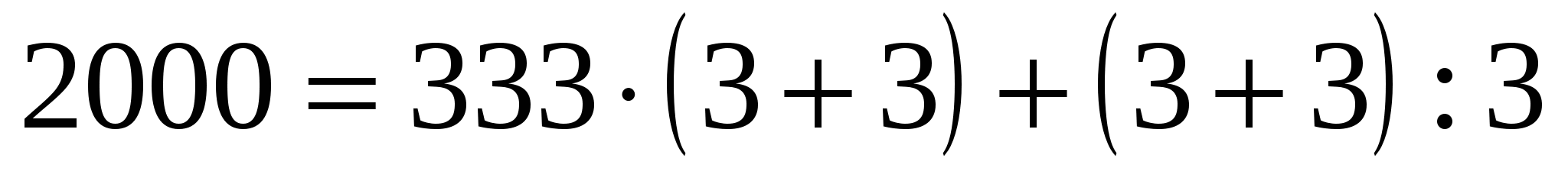 .
.
-
Ответ:
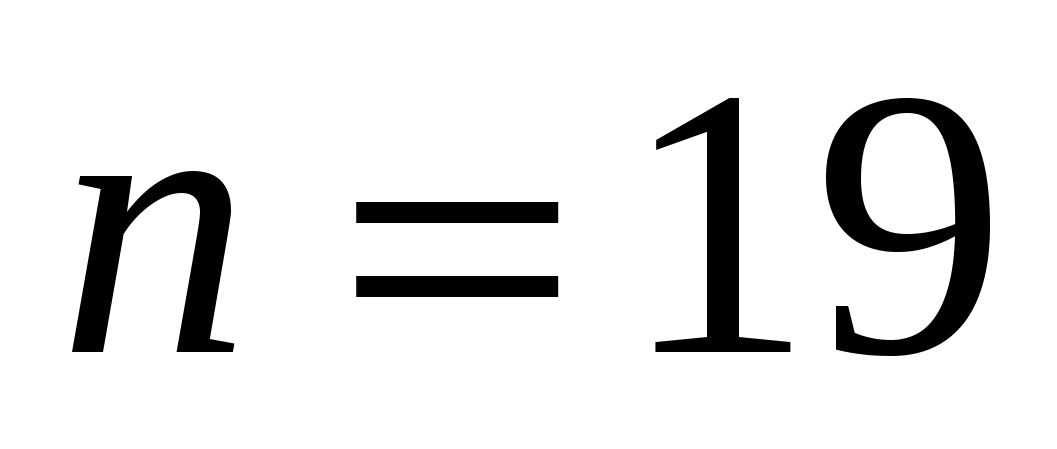 .
.
3. Ответ:
составим сумму:
![]()
По условию число ![]() делится на 37, поэтому и сумма
делится на 37, поэтому и сумма
![]() делится на 37.
делится на 37.
4. Ответ: нужно исключить три числа, например 3, 7 и 11. Подойдут
группы, произведение чисел в которых равно 1440, например {4, 5, 8, 9}
и {2, 6, 10, 12}. Очевидно, что числа 7 и 11 должны быть исключены.
Произведение остальных чисел есть ![]() , поэтому ещё необходимо
, поэтому ещё необходимо
исключить число 3 или 12 (так как в произведение число 3 входит в
нечётной степени).
5. Ответ: 1, 5 и 8 лет.
Если первенец старше второго ребёнка на x лет, а средний старше
третьего ребёнка на y лет, то 70 – 45=3(x + y) + y, так как возраст
каждого из родителей и старшего ребёнка к моменту рождения третьего
ребёнка увеличился на (x + y) лет, а возраст второго – на y лет.
Аналогично (x + y + 1) + (y + 1) + 1 = 14. Мы получили систему
уравнений 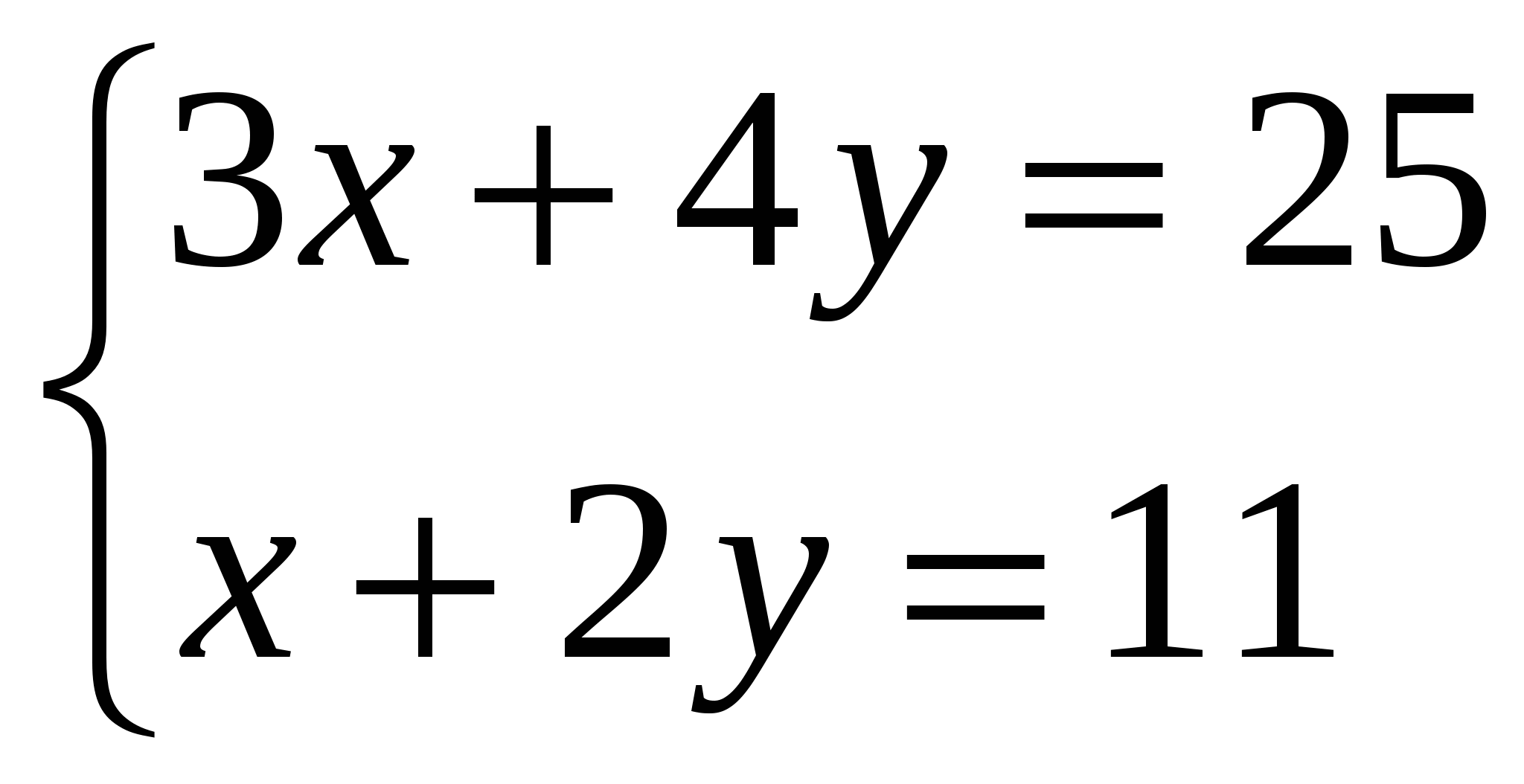 , из которой x = 3, y = 4.
, из которой x = 3, y = 4.
-
Ответ: 4 см.
Восстановим перпендикуляры из точек А и В. Рассмотрим образовавшийся зеленый прямоугольник.
Видно, что его площадь равна площади MBPA и следовательно, равна одной трети площади большого квадрата и равна (6 · 6) : 3 = 12 кв.см.
Высота зеленого прямоугольника равна 6 : 2 = 3 (см). Длина его второй
стороны АВ равна 12 кв.см : 3 см = 4 см.
Список использованной литературы
1. Агаханов Н.Х., Терешин Д.А., Кузнецова Г.М. Школьные математические
олимпиады. – М.: Дрофа, 1999.
2. Горбачёв Н.В. Сборник олимпиадных задач по математике. – М.: МЦНМО,
2004.
3. Агаханов Н.Х., Подлипский О.К. Математика. Районные олимпиады.
6 – 11 классы. – М.: Просвещение, 2010
Здесь представлены материалы теста на тему «Олимпиадные задания по математике для учащихся 8-ых классов», которые могут быть просмотрены в онлайн режиме или же их можно бесплатно скачать. Предмет теста: Математика (8 класс). Также здесь Вы найдете подборку тестов на схожие темы, что поможет в еще лучшей подготовке к тестированию.

