Олимпиадные задания по математике 5-ы (2014-2015 учебный год)
Математика 2014-2015 учебный год
5 класс
Задача 1: Сколько трёхзначных чисел можно составить из цифр 2,4,6,8, если цифры в записи числа не повторяются?
Задача 2: Сегодня Сереже исполнилось 10 лет, а Вове – 1 год. Каков будет возраст Сережи, когда он станет втрое старше Вовы?
Задача 3: Составьте из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 магический квадрат, то есть разместите их в таблице 3 × 3 так, чтобы суммы чисел по строкам, столбцам и двум диагоналям были одинаковы.
Задача 4: Девочка заменила каждую букву в своем имени ее номером в русском алфавите и получила число 2011533. Как ее зовут? Имеет ли задача однозначный ответ? Почему?
Задача 5: Школьники посадили вдоль дороги (по прямой) 25 деревьев. Расстояние между двумя любыми соседними деревьями одинаковое. Найдите это расстояние, если между крайними деревьями 600 дм.
6 класс
Задача 1: В правление фирмы входят 9 человек. Из своего состава правление должно выбрать президента и вице-президента. Сколькими способами это можно сделать?
Задача 2: Найдите пропущенное число:
| 60 | 17 | |
| 16 | | 14 |
| 20 | 14 | |
| 19 | | 31 |
Задача 3: Петя говорит: позавчера мне еще было 10 лет, а в следующем году мне исполнится 13. Может ли такое быть?
Задача 4: В портовом городе начинаются три туристских теплоходных рейса, первый из которых длится 15 суток, второй – 20 суток и третий – 12 суток. Вернувшись в порт, теплоходы в этот день снова отправляются в рейс. Сегодня из порта вышли теплоходы по всем маршрутам. Через сколько суток они впервые снова вместе уйдут в плавание?
Задача 5: Немецкого учёного Карла Гаусса называли королём математиков. Однажды в школе (Гауссу тогда было 10 лет) учитель предложил классу сложить все числа от 1до 100. пока он диктовал задание, у Гаусса уже был готов ответ. Попробуйте догадаться, как Карл Гаусс складывал числа от 1 до 100 и запишите результат вычислений.
7 класс
Задача 1: Составьте числовое выражение, значение которого равно 100, используя цифры 1,2,3,4,5 и не меняя порядок их следования
Задача 2: На двух кустах сидело 25 воробьев. После того как с первого куста перелетело на второй 5, а со второго улетело 7 воробьев, то на первом кусте осталось вдвое больше воробьев, чем на втором. Сколько воробьев было на каждом кусте первоначально?
Задача 3: Из 35 учащихся класса 22 выписывают журнал, 27 – газету, а 3 ученика не выписывают ни газету, ни журнал. Сколько учащихся выписывают и газету, и журнал?
Задача 4: Дана точка М(1,5). Найдите координаты точек L и N таких, что МN= =2МL, если NL=10,5. сколько решений имеет задача?
Задача 5: Сколько нечётных четырёхзначных чисел можно составить из цифр 0,1,2,3,4?
8 класс
1. Расставьте скобки и знаки арифметических действий так, чтобы получилось правильное равенство:
![]()
2. Петя тратит 1/3 своего времени на игру в футбол, 1/5 — на учебу в школе, 1/6 — на просмотр кинофильмов, 1/7 — на решение олимпиадных задач, и 1/3 — на сон. Можно ли так жить?
3. У колхозника было несколько одинакового веса поросят и несколько ягнят также одинакового веса. Пионер спросил колхозника, сколько весит один поросенок и один ягненок. Колхозник ответил, что 3 поросенка и 2 ягненка весят 22 кг, а 2 поросенка и 3 ягненка весят 23 кг. Как узнать, сколько весит один поросенок и сколько весит один ягненок?
4. Один из углов треугольника на 120° больше другого. Докажите, что биссектриса треугольника, проведённая из вершины третьего угла, вдвое длиннее, чем высота, проведенная из той же вершины.
5. У подводного царя служат осьминоги с шестью, семью или восемью ногами. Те, у кого 7 ног, всегда лгут, а у кого 6 или 8 ног, всегда говорят правду. Встретились четыре осьминога. Синий сказал: "Вместе у нас 28 ног", зеленый: "Вместе у нас 27 ног", желтый: "Вместе у нас 26 ног", красный: "Вместе у нас 25 ног". У кого сколько ног?
9 класс
1. Решить уравнение ( х 2 + 6 х - 4)( х 2 + 6 х - 3) = 12
2. В плоскости расположено 11 зубчатых колёс таким образом, что первое колесо сцеплено своими зубцами со вторым, второе — с третьим и т.д. Наконец, последнее, одиннадцатое, колесо сцеплено с первым. Могут ли вращаться колёса такой системы?
3. В треугольнике АВС медиана ВМ в два раза меньше стороны АВ и образует с ней угол 40o . Найдите угол АВС .
4. Какое наибольшее число белых и черных фишек можно расставить на шахматной доске так, чтобы на любой горизонтали и на любой вертикали белых фишек было ровно в два раза больше, чем черных?
5. Три друга сделали по одному заявлению про целое число х. Петя: «Число х больше 4, но меньше 8». Вася: «Число х больше 6, но меньше 9». Толя: «Число х больше 5, но меньше 8». Найдите число х, если известно, что двое из друзей сказали правду, а третий солгал. Нужно не только проверить, что найденное число годится, но и объяснить, почему другие варианты ответа невозможны.
Решение
5 класс
Задача: Сколько трехзначных чисел можно составить из цифр 2.4,6,8, если цифры в записи числа не повторяются?
Решение: стр. 39 учебника, 4*3*2= 24 трехзначных числа
Задача : Сегодня Сереже исполнилось 10 лет, а Вове – 1 год. Каков будет возраст Сережи, когда он станет втрое старше Вовы?
Решение: Серёже-15, Вове 5 через 5 лет
Задача: Составьте из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 магический квадрат, то есть разместите их в таблице 3 × 3 так, чтобы суммы чисел по строкам, столбцам и двум диагоналям были одинаковы.
Решение:

Задача: Девочка заменила каждую букву в своем имени ее номером в русском алфавите и получила число 2011533. Как ее зовут? Имеет ли задача однозначный ответ? Почему?
Решение: Таня, зависит от того, как читать числа
Задача: Школьники посадили вдоль дороги (по прямой) 25 деревьев. Расстояние между двумя любыми соседними деревьями одинаковое. Найдите это расстояние, если между крайними деревьями 600 дм.
Решение: 600:24 = 25 дм – расстояние между двумя любыми соседними деревьями.
6 класс
Задача: В правление фирмы входят 9 человек. Из своего состава правление должно выбрать президента и вице-президента. Сколькими способами это можно сделать?
Решение: Президентом фирмы можно избрать одного из 9 человек, и для каждого выбранного президента 8 способами можно выбрать вице- президента.Значит: 9х8=72 способа
Задача: Найдите пропущенное число:
Решение: 60- удвоенная сумма крайних чисел; 20- полусумма крайних чисел
Задача: Петя говорит: позавчера мне еще было 10 лет, а в следующем году мне исполнится 13. Может ли такое быть?
Решение: Да, может, если день рождения Пети – 31 декабря, а указанную фразу он произносит 1 января.
Задача : В портовом городе начинаются три туристских теплоходных рейса, первый из которых длится 15 суток, второй – 20 суток и третий – 12 суток. Вернувшись в порт, теплоходы в этот день снова отправляются в рейс. Сегодня из порта вышли теплоходы по всем маршрутам. Через сколько суток они впервые снова вместе уйдут в плавание?
Решение: НОК=60 суток
Задача : Немецкого учёного Карла Гаусса называли королём математиков. Однажды в школе (Гауссу тогда было 10 лет) учитель предложил классу сложить все числа от 1до 100. пока он диктовал задание, у Гаусса уже был готов ответ. Попробуйте догадаться, как Карл Гаусс складывал числа от 1 до 100.
Решение: (1+99) + (2+98) + (3+97) + … + 100 +50 =5050
7 класс
Задача : Составьте числовое выражение, значение которого равно 100, используя цифры 1,2,3,4,5 и не меняя порядок их следования
Решение: (1+23-4) х 5 =100
Задача : На двух кустах сидело 25 воробьев. После того как с первого куста перелетело на второй 5, а со второго улетело 7 воробьев, то на первом кусте осталось вдвое больше воробьев, чем на втором. Сколько воробьев было на каждом кусте первоначально?
Решение: Пусть x – количество воробьёв на первом кусте. Тогда x – 5 = 2 × (25 – (x – 5 + 7)). Решаем, и получаем, что x = 17.
Задача : Из 35 учащихся класса 22 выписывают журнал, 27 – газету, а 3 ученика не выписывают ни газету, ни журнал. Сколько учащихся выписывают и газету, и журнал?
Решение:
35-3=32 что-нибудь выписывают
32-22=10 только газету
32-27=5 только журнал
10+5 = 15 или газету или журнал
32-15=17 и газету и журнал
Задача : Дана точка М(1,5). Найдите координаты точек L и N таких, что М N =2МL, если NL=10,5. сколько решений имеет задача?
Решение: 4 решения в зависимости от того как расположены точки
Задача : Сколько нечётных четырёхзначных чисел можно составить из цифр 0,1,2,3,4?
Решение: На первом месте в записи числа может стоять любая цифра, кроме нуля, - 4 варианта. На втором и третьем местах – любая из пяти цифр. Так кА число нечётное, то на последнем месте могут быть только цифры 1 или 3 – т.е. получаем ещё два варианта: 4 х5 х5х 2=200
8 класс
1. ![]()
2. Петя тратит 1/3 своего времени на игру в футбол, 1/5 — на учебу в школе, 1/6 — на просмотр кинофильмов, 1/7 — на решение олимпиадных задач, и 1/3 — на сон. Можно ли так жить?
Решение Поскольку 1/5 + 1/6 > 1/3, то сумма данных дробей 1/3 + 1/5 + 1/6 + 1/7 + 1/3 > 1, что противоречит здравому смыслу. Нет, так жить нельзя.
3. У колхозника было несколько одинакового веса поросят и несколько ягнят также одинакового веса. Пионер спросил колхозника, сколько весит один поросенок и один ягненок. Колхозник ответил, что 3 поросенка и 2 ягненка весят 22 кг, а 2 поросенка и 3 ягненка весят 23 кг. Как узнать, сколько весит один поросенок и сколько весит один ягненок?
Решение. Если сложить вес трех поросят и двух ягнят с весом двух поросят и трех ягнят, то получим вес пяти поросят и пяти ягнят, равный 45 кг. Значит, один поросенок и один ягненок весят 9 кг, а два поросенка и два ягненка весят 18 кг. Вычтя это из первого данного веса, получим вес поросенка, равный 4 кг. Тогда ягненок весит 5 кг.
4. Один из углов треугольника на 120° больше другого. Докажите, что биссектриса треугольника, проведённая из вершины третьего угла, вдвое длиннее, чем высота, проведенная из той же вершины.
Решение
Пусть ABC — данный треугольник, ![]() B = a,
B = a, ![]() A = 120° + a. Тогда
A = 120° + a. Тогда ![]() C = 60° - 2a. Если CL — биссектриса данного треугольника, то
C = 60° - 2a. Если CL — биссектриса данного треугольника, то ![]() CLA =
CLA = ![]() LCB +
LCB + ![]() LBC = (30° - a) + a = 30°. Пусть CH - высота треугольника АВС, тогда в треугольнике CLH катет CH, лежащий против угла в 30°, в два раза меньше, чем гипотенуза CL.
LBC = (30° - a) + a = 30°. Пусть CH - высота треугольника АВС, тогда в треугольнике CLH катет CH, лежащий против угла в 30°, в два раза меньше, чем гипотенуза CL.
5. Три друга сделали по одному заявлению про целое число х. Петя: «Число х больше 4, но меньше 8». Вася: «Число х больше 6, но меньше 9». Толя: «Число х больше 5, но меньше 8». Найдите число х, если известно, что двое из друзей сказали правду, а третий солгал. Нужно не только проверить, что найденное число годится, но и объяснить, почему другие варианты ответа невозможны.
Ответ: 6. Решение. Ясно, что число х должно быть больше 4, но меньше 9, иначе все солгали. Поэтому для числа х есть всего четыре возможности: 5, 6, 7, 8. Если х=5, то правду сказал только Петя. Если х=8, то правду сказал только Вася. Если х=7, то правду сказали все трое. И только при х=6 правду скажут двое: Петя и Толя.
9 класс
1. Решить уравнение ( х 2 + 6 х - 4)( х 2 + 6 х - 3) = 12
Решение. Раскрывать скобки не имеет смысла, так как получится уравнение четвертой степени. В таких случаях применяется метод подстановки, ведь в скобках присутствует одинаковый блок х 2 + 6 х .
Обозначая х 2 + 6 х = у , получим уравнение ( у - 4)( у - 3) = 12, отсюда у ( у - 7) = 0, у 1 = 0, у 2 = 7. Делаем обратную замену х 2 + 6 х = у . Если х 2 + 6 х = 0, то х 1 = 0, х 2 = - 6. Если х 2 + 6 х = 7, то, решая квадратное уравнение х 2 + 6 х - 7 = 0, получим х 1 = 0, х 2 = - 6, х 3 = -7, х 4 = 1 . Ответ: 0, -6, -7, 1
2. В плоскости расположено 11 зубчатых колёс таким образом, что первое колесо сцеплено своими зубцами со вторым, второе — с третьим и т.д. Наконец, последнее, одиннадцатое, колесо сцеплено с первым. Могут ли вращаться колёса такой системы?
Решение: нет. Соседние колёса должны вращаться в противоположных направлениях. Поэтому колёса с номерами 1 и 11 должны вращаться в одном направлении (все колёса с нечётными номерами вращаются в одном направлении, а с чётными — в противоположном). С другой стороны, колёса с номерами 1 и 11 соседние, поэтому они должны вращаться в противоположных направлениях.
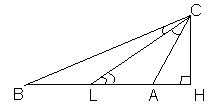
3. В треугольнике АВС медиана ВМ в два раза меньше стороны АВ и образует с ней угол 40o . Н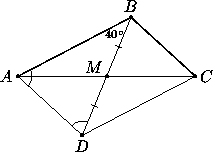 айдите угол АВС .
айдите угол АВС .
Решение Продлим медиану BM за точку M на ее длину и получим точку D (см. рис.). Так как AB = 2BM , то AB = BD , то есть треугольник ABD — равнобедренный. Следовательно, ![]() BAD =
BAD = ![]() BDA = (180o - 40o) : 2 = 70o .
BDA = (180o - 40o) : 2 = 70o .
Четырёхугольник ABCD является параллелограммом, так как его диагонали точкой пересечения делятся пополам. Значит, ![]() CBD =
CBD = ![]() ADB = 70o . Тогда
ADB = 70o . Тогда ![]() ABC =
ABC = ![]() ABD +
ABD + ![]() CBD = 110o . Ответ 110o .
CBD = 110o . Ответ 110o .
4. Какое наибольшее число белых и черных фишек можно расставить на шахматной доске так, чтобы на любой горизонтали и на любой вертикали белых фишек было ровно в два раза больше, чем черных?
Решение Число фишек на каждой вертикали кратно 3, значит, их не больше 6, а на всей доске - не более 48. Пример расстановки 48 фишек: 32 белые фишки ставим на белые поля, а 16 черных - вдоль главной "черной" диагонали и вдоль двух параллельных диагоналей "длины" 4.Ответ48 фишек.
5. У подводного царя служат осьминоги с шестью, семью или восемью ногами. Те, у кого 7 ног, всегда лгут, а у кого 6 или 8 ног, всегда говорят правду. Встретились четыре осьминога. Синий сказал: "Вместе у нас 28 ног", зеленый: "Вместе у нас 27 ног", желтый: "Вместе у нас 26 ног", красный: "Вместе у нас 25 ног". У кого сколько ног?
Решение Так как осьминоги противоречат друг другу, то возможны два случая: либо все осьминоги лгут, либо ровно один из них говорит правду. Если все осьминоги лгут, то у каждого из них по 7 ног. Значит, вместе у них 28 ног. Но тогда синий осьминог сказал правду - противоречие.
Если же три осьминога солгали, а четвёртый сказал правду, то у солгавших осьминогов должно быть по 7 ног, а у сказавшего правду - либо 6, либо 8. Поэтому вместе у них либо 27, либо 29 ног, то есть правду сказал зелёный осьминог. Таким образом, у зелёного осьминога 6 ног, а у остальных по 7 ног.
Здесь представлены материалы теста на тему «Олимпиадные задания по математике 5-ы (2014-2015 учебный год)», которые могут быть просмотрены в онлайн режиме или же их можно бесплатно скачать. Предмет теста: Математика (5 класс). Также здесь Вы найдете подборку тестов на схожие темы, что поможет в еще лучшей подготовке к тестированию.

