Презентация "Многокритериальные задачи. Метод ограничений" – проект, доклад
Презентацию на тему "Многокритериальные задачи. Метод ограничений" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Разные. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 19 слайд(ов).
Слайды презентации
Список похожих презентаций
Метод синектики
СИНЕКТИКА. метод коллективной творческой деятельности, основанный на целенаправленном использовании интуитивно-образного, метафорического мышления ...Метод наблюдения
Наблюдение – это…. метод познания какого-либо процесса или явления путем целенаправленного, планомерного, непосредственного их восприятия, прослеживания ...Метод наблюдения
Наблюдение. общенаучный метод исследования. Он применяется и как ведущий метод, и как дополнительный – подкрепляющий (например, при опросе). Он является ...Метод математического моделирования
Моделирование. исследование объектов познания на их моделях; построение и изучение моделей реально существующих объектов, процессов или явлений с ...Метод мозгового штурма
Сущность метода мозгового штурма заключается в том, что отбирается группа квалифицированных экспертов, но оценки и выводы делаются в ходе заседания. ...Метод фокальных объектов
– метод поиска новых идей путем присоединения к исходному объекту свойств или признаков случайных объектов. Применяется при поиске новых модификаций ...Итерационные методы решения линейных алгебраических систем1. Метод простой итерации или метод Якоби
Предположим, что диагональные элементы матриц A исходной системы не равны 0 (aii ≠ 0, i = 1, 2, …, n). Разрешим первое уравнение системы относительно ...Метод Дельфи
Метод Дельфи (иногда дельфийский метод) был разработан в 1950—1960 годы в США для прогнозирования влияния будущих научных разработок на методы ведения ...Метод Дельфи
История разработки метода. Метод Дельфи разрабатывался в 50-60-е годы XX века в США. Основной его задачей было прогнозирование воздействия научных ...Метод парных сравнений
Согласно методу осуществляются парные сравнения целей во всех возможных сочетаниях. В каждой паре выделяется наиболее предпочтительная цель. Конечная ...Метод «Морфологический анализ»
Создание метода. В современном виде морфоанализ создан швейцарским астрофизиком Ф. Цвикки. В 30-е годы ХХ века Ф. Цвикки интуитивно применил морфологический ...Метод исследования: Эксперимент
Эксперимент- один из основных методов научного познания вообще, психологического исследования в частности. ЭКСПЕРИМЕНТ (от лат. experimentum — проба, ...Менеджмент-цели и задачи
Задачи и цели менеджмента. Задачами менеджмента - как науки являются разработка, экспериментальная проверка и применение на практике научных подходов, ...Маркетинг взаимоотношений: цели, задачи, содержание
. Планирование создания ценности. Пять «К» и одно «Г» Кто – покупатель, в котором заинтересована фирма, каков его портрет Какие – товары или услуги, ...Метод Сократа
Сократ — жил в 469-399 годах до нашей эры. Древнегреческий философ из Афин, один из родоначальников диалектики. Сократ утверждал, что сам он «ничего ...Метод капитализации доходов
Это метод оценки, применяемый в рамках доходного подхода, при котором стоимость объекта определяется путем деления текущих (за год) доходов, от использования ...Метод управленческого консультирования. Консалтинг.
Метод управленческого консультирования. Управленческое консультирование - это предоставление независимых советов и помощи по вопросам управления, ...Метод контрольных вопросов (МКВ)
«Вопрос есть повивальная бабка, помогающая родиться новой мысли…» Сократ. Древнегреческий философ Сократ умел в диалоге так искусно задавать вопросы, ...Метод эквивалентного генератора
Суть метода эквивалентного генератора состоит в нахождении тока в одной выделенной ветви, при этом остальная часть сложной электрической цепи заменяется ...Занимательные задачи по информатике
В настоящее время главным стратегическим направлением развития системы школьного образования в России является личностно-ориентированное образование ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:19 июня 2019
Категория:Разные
Содержит:19 слайд(ов)
Поделись с друзьями:
Скачать презентацию





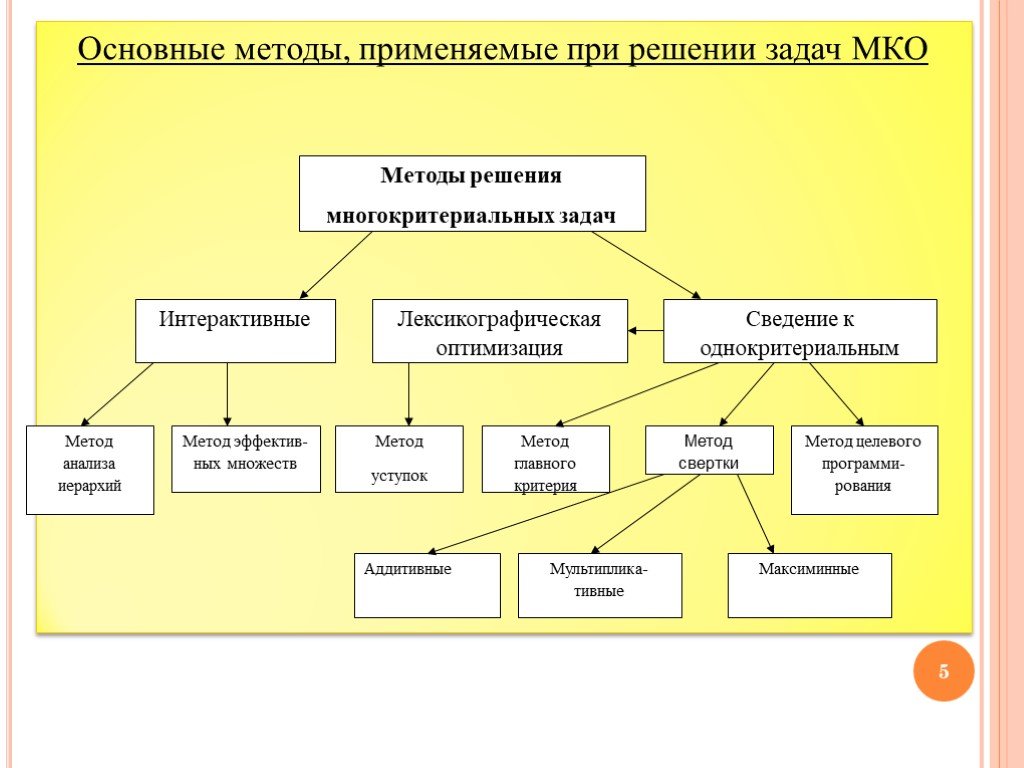
















![Рассмотрим задачу многокритериальной оптимизации min Х? ? ? Ф Х =Ф Х ∗ , (1) где Ф Х =( ф 1 Х , ф 2 Х ,…, ф ? Х ) — векторный критерий оптимальности, ф ? Х , ??[1,?] — частные критерии оптимальности (скалярные), ? Х — множество допустимых значений вектора варьируемых параметров. Рассмотрим задачу многокритериальной оптимизации min Х? ? ? Ф Х =Ф Х ∗ , (1) где Ф Х =( ф 1 Х , ф 2 Х ,…, ф ? Х ) — векторный критерий оптимальности, ф ? Х , ??[1,?] — частные критерии оптимальности (скалярные), ? Х — множество допустимых значений вектора варьируемых параметров.](https://prezentacii.org/upload/cloud/19/06/155477/images/thumbs/screen8.jpg)




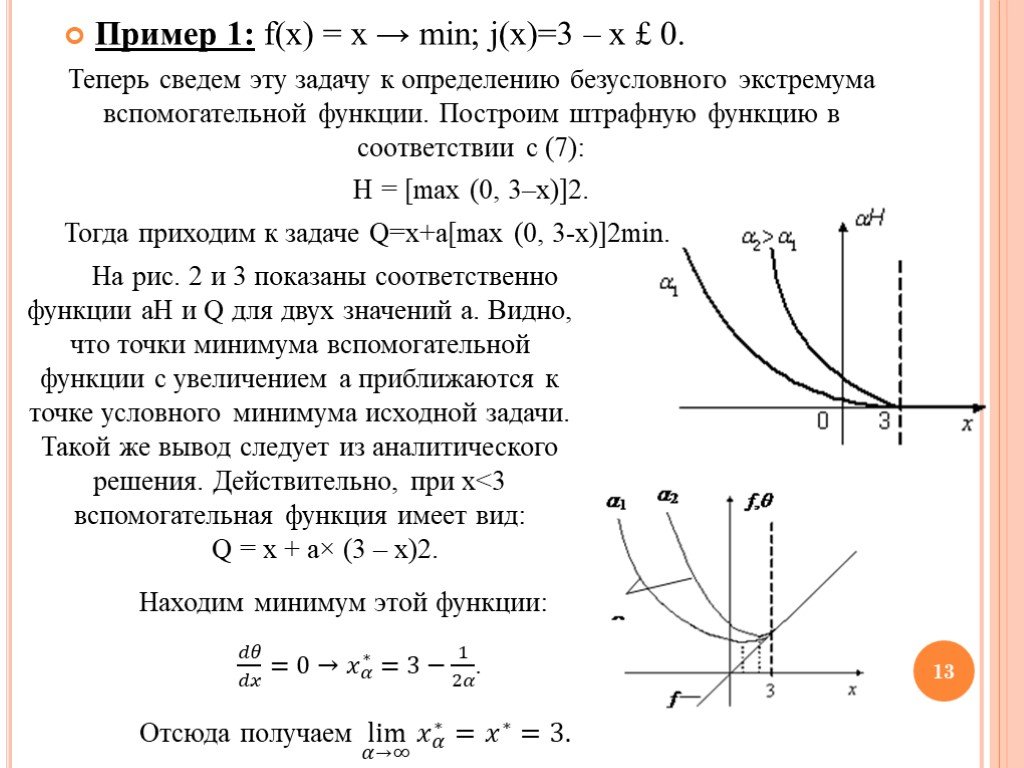
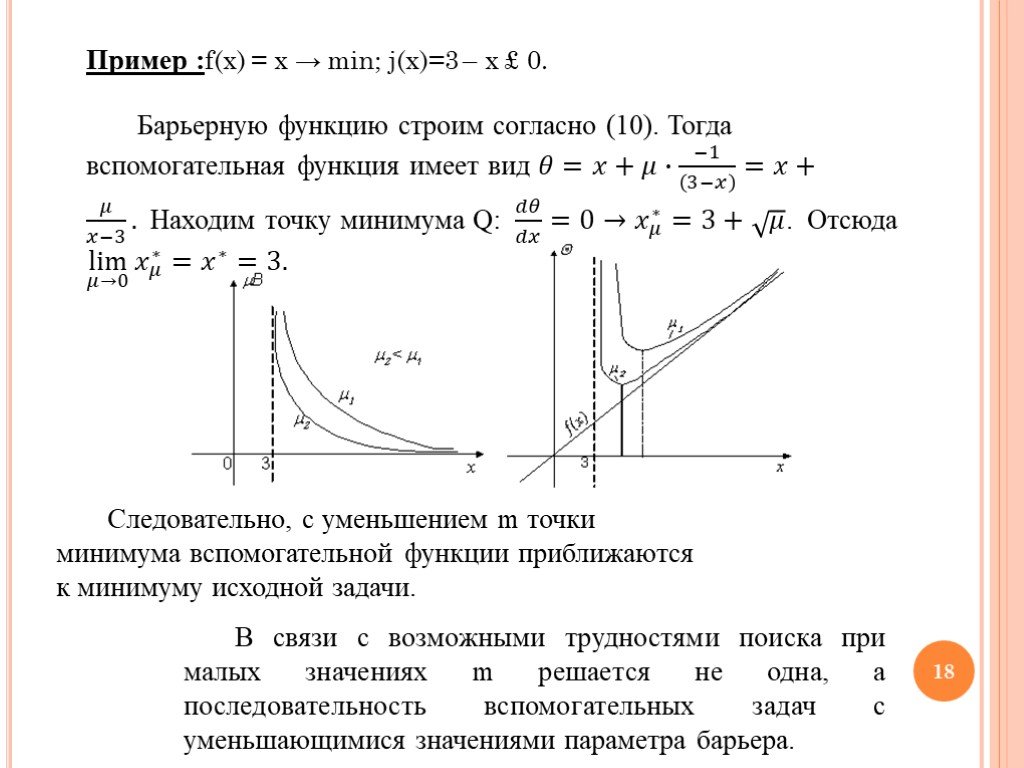
![Пример 1: f(x) = x → min; j(x)=3 – x £ 0. Теперь сведем эту задачу к определению безусловного экстремума вспомогательной функции. Построим штрафную функцию в соответствии с (7): H = [max (0, 3–x)]2. Тогда приходим к задаче Q=x+a[max (0, 3-x)]2min. На рис. 2 и 3 показаны соответственно функции aH и Q Пример 1: f(x) = x → min; j(x)=3 – x £ 0. Теперь сведем эту задачу к определению безусловного экстремума вспомогательной функции. Построим штрафную функцию в соответствии с (7): H = [max (0, 3–x)]2. Тогда приходим к задаче Q=x+a[max (0, 3-x)]2min. На рис. 2 и 3 показаны соответственно функции aH и Q](https://prezentacii.org/upload/cloud/19/06/155477/images/thumbs/screen13.jpg)



































