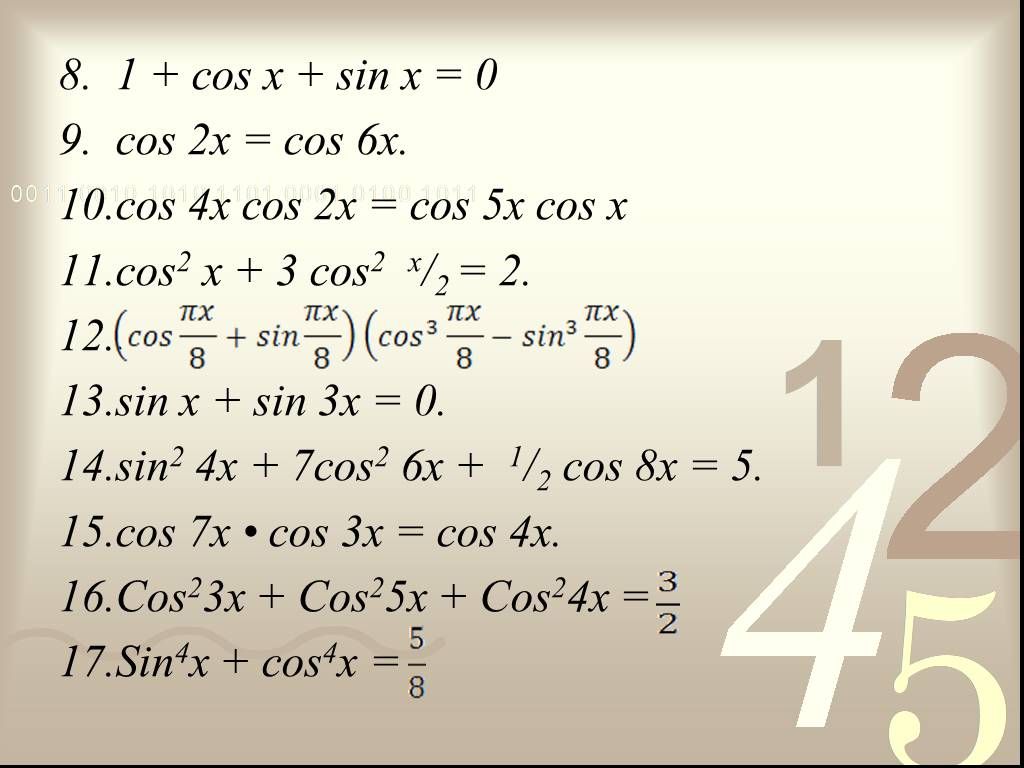Презентация "Решение тригонометрических уравнений при помощи формулы понижения степени." – проект, доклад
Презентацию на тему "Решение тригонометрических уравнений при помощи формулы понижения степени." можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Разные. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 20 слайд(ов).
Слайды презентации
Список похожих презентаций
Осмотр наружных половых органов, влагалища и шейки матки при помощи зеркал
Для проведения гинекологического осмотра пациентке предлагают расположиться на гинекологическом кресле. Гинекологический осмотр проводят при помощи ...Основные возражения при продаже. Oriflame
Что вы узнаете на тренинге:. Что такое возражение? Истинная причина возражений Как с ними работать? Практика. Возражение — это хороший знак, гораздо ...Организация медицинской помощи сельскому населению
Цель лекции. Ознакомить студентов с особенностями организации медицинской помощи жителям села. План лекции. 1.Факторы, определяющие особенности в ...Общие меры безопасности при производстве работ и нахождении на железнодорожных путях
Общие требования безопасности для работников железнодорожного транспорта при нахождении на путях во время исполнения служебных обязанностей. Прежде ...Методы исследования при заболеваниях сердечнососудистой системы
В диагностическом процессе при заболеваниях сердечнососудистой системы используются как субъективные и объективные методы исследования больного, так ...Массаж при заболеваниях и повреждениях мышц
Массаж при ушибах и растяжениях связок и мышц. При свежей травме мягких тканей, растяжении сумочно-связочного аппарата без нарушения его целости к ...ЛФК при гипертензии
Гипертензия – повышенное гидростатическое давление в полых органах, сосудах и полостях организма. Такое заболевание может привести к сердечному приступу, ...Первая помощь при солнечном и тепловом ударе
Солнечный удар. Солнечный удар — болезненное состояние, расстройство работы головного мозга вследствие продолжительного воздействия солнечного света ...Гласные в приставках пре - и при -.
При- обозначает 1.присоединение: прибить пришить прикрепить. 2.приближение: прискакать примчаться прилететь. 3.близость: пришкольный приречной приморский. ...Виды работ педагога-психолога при реализации основных направлений деятельности
Группы работ по психологическому сопровождению образования. Оказание психологической помощи и повышение психологической компетентности участников ...Взаимодействие элементов ЗРС СД-ДД при ее функционировании
Занятие №6 Взаимодействие элементов ЗРС СД-ДД при её функционировании. Учебные вопросы: 1. Обеспечение целеуказанием с КП системы 2. Поиск, обнаружение ...Ведение внебольничных родов. Неотложная помощь при задержке отделившегося последа
Транспортировка беременных средствами скорой медицинской помощи. Не все беременные с предвестниками родов госпитализируются машиной скорой помощи, ...Биохимические исследования при заболеваниях печени
Печень играет важную роль в обмене белков, углеводов, липидов. Клетки печени метаболизируют, детоксицируют и экскретируют экзо- и эндогенные вещества. ...Алгоритм действий при тяжелой преэклампсии (догоспитальная помощь)
КРИТЕРИИ ДИАГНОСТИКИ ЭКЛАМПСИИ (на догоспитальном этапе). Подергивание мышц лица, судороги (тонические или тонико-клонические), потеря сознания в ...Острые аллергические реакции в практике фельдшера скорой помощи
цель: Изучить особенности клинического течения острых аллергических реакций, алгоритмы скорой и неотложной помощи, показать, что повышение качества ...Первая медицинская помощь при ушибах, вывихах, растяжениях
Ушибы - повреждения тканей и органов, при которых не нарушена целость кожи и костей. Клинические признаки на месте ушиба быстро появляется припухлость, ...Деятельность медицинской сестры в профилактике осложнений при проведении инвазивных манипуляций
Актуальность. обусловлена тем, что несмотря на значительный прогресс медицины, увеличение объема медицинской помощи, оказываемой населению, повышение ...Аварийно-спасательные работы при пожарах
Классификация пожаров. Пожаром называется неконтролируемое горение, причиняющее материальный ущерб, вред жизни и здоровью граждан, интересам общества ...Диета при заболевании сахарным диабетом
Одним из обязательных компонентов лечения (образа жизни) при сахарном диабете является рациональное питание (диета). Во многих случаях, одно только ...ЛФК при травмах позвоночника
Травмы опорно-двигательного аппарата вызывают нарушения анатомической целости тканей и их функций, сопровождаются как местной, так и общей реакцией ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:17 марта 2019
Категория:Разные
Содержит:20 слайд(ов)
Поделись с друзьями:
Скачать презентацию