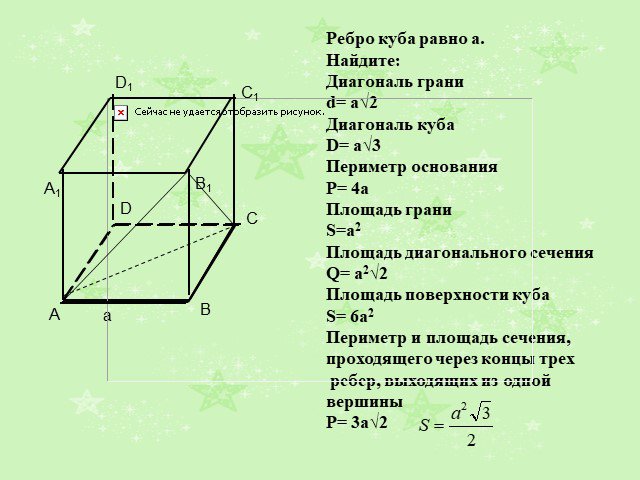
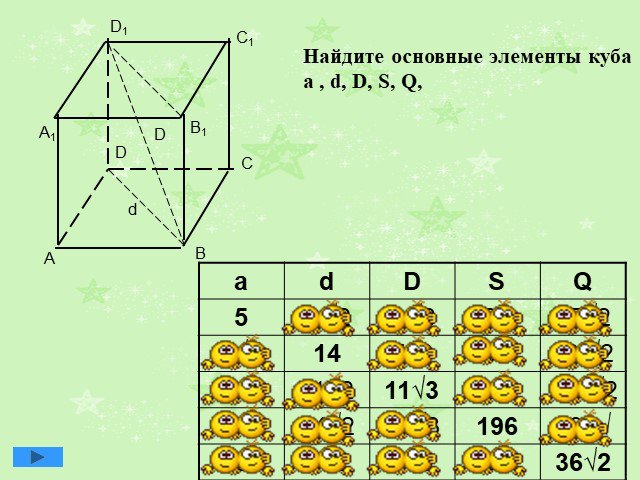
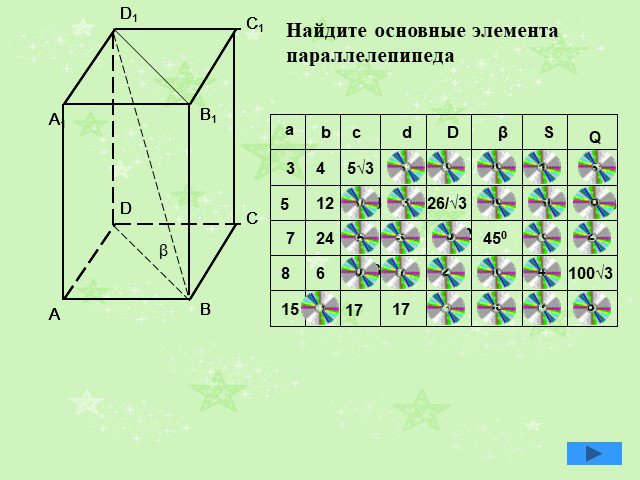
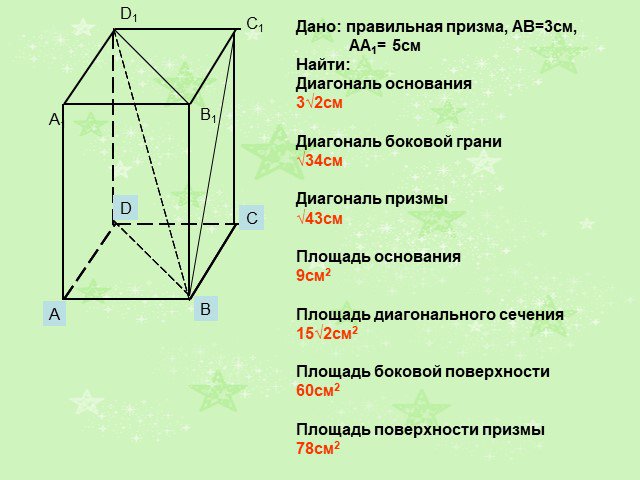
Презентация "Решения задач по теме «Призма»" по математике – проект, доклад
Презентацию на тему "Решения задач по теме «Призма»" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 14 слайд(ов).
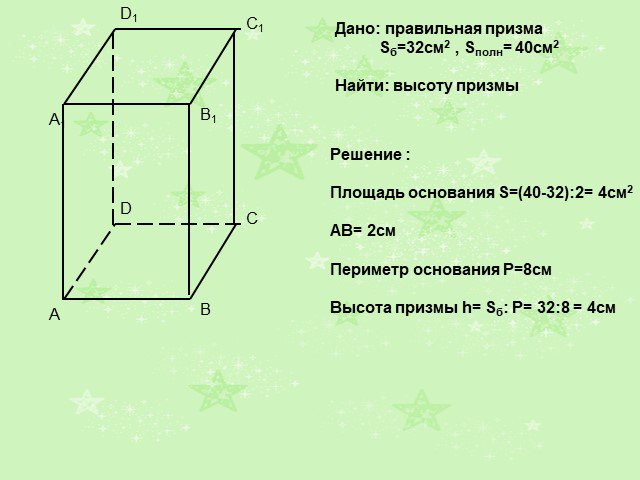
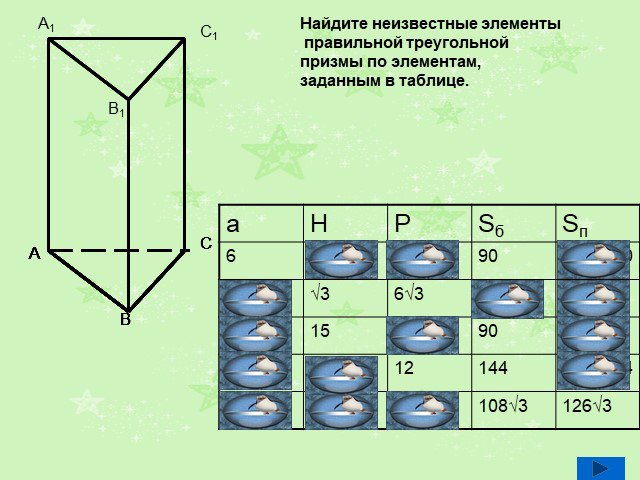
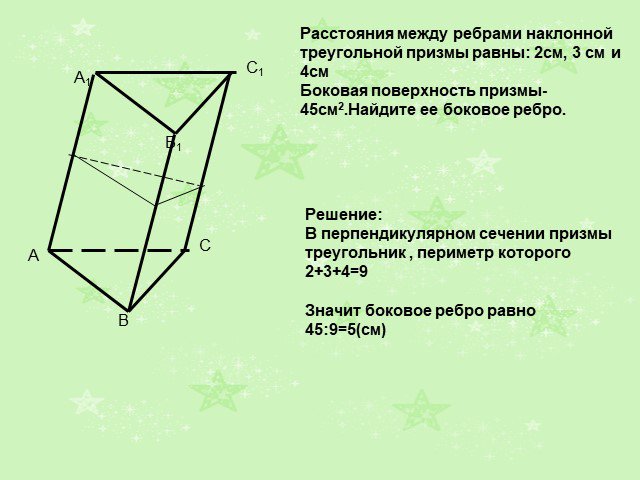
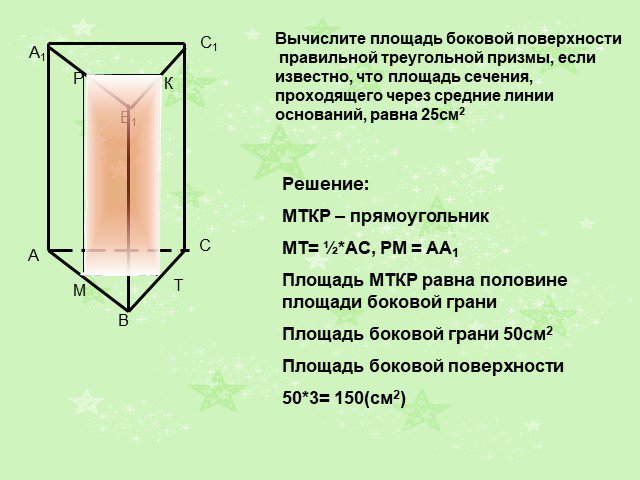
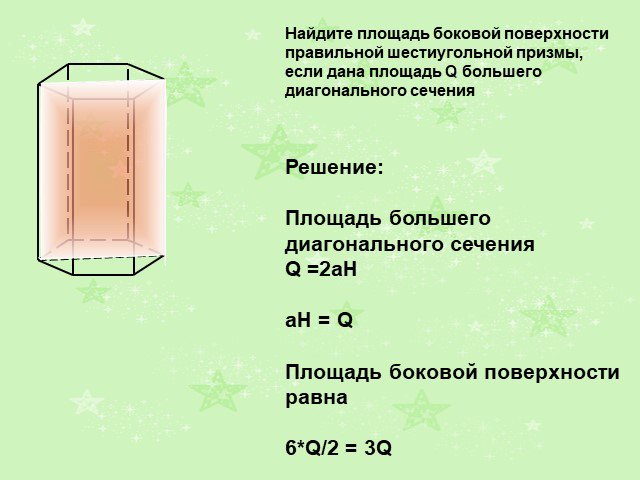
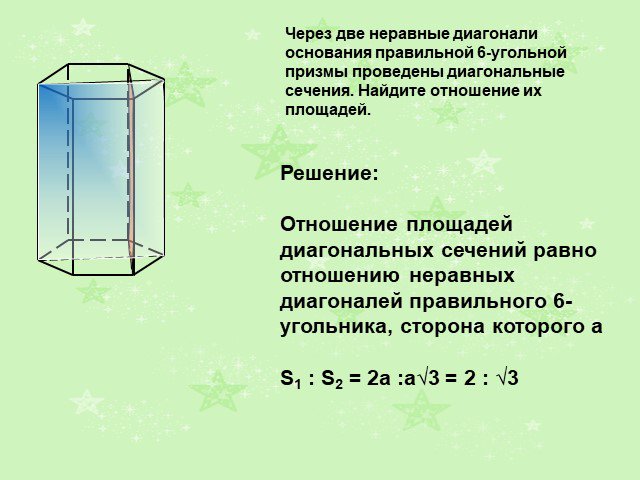
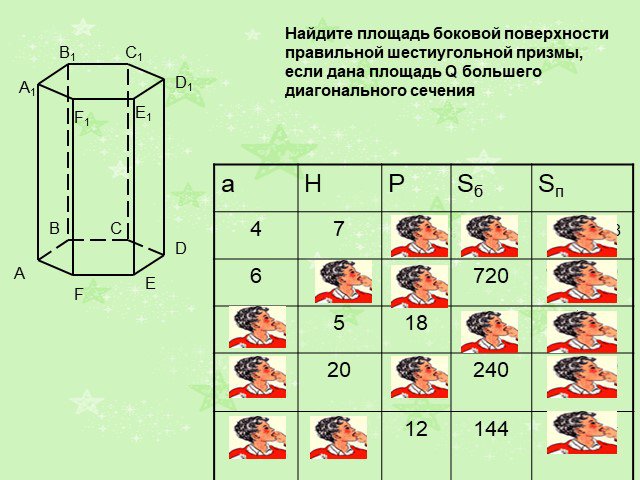
Слайды презентации
Список похожих презентаций
ГИА-2012. Решение задач по теме "Чтение графиков функций"
График какой из приведенных ниже функций изображен на рисунке? Задание 17 (№ 197785). Задание 17 (№ 193087). Задание 17 (№ 197695). Задание 17 (№ ...Алгоритм решения задач на пропорции
Эпиграф: «Математика обладает двумя великими сокровищами. Первое-это теорема Пифагора, второе-деление отрезка в крайнем и среднем отношении.» Иоганн ...«Решение задач с помощью пропорций»
Найти значение Х: Х:3=4:6 5:Х=2:6 7:3=Х:18 Устная работа. Указать вид пропорциональной зависимости:. Какова зависимость пути от времени? Какова зависимость ...«Решение задач по математике»
10 февраля. В классе. Задача условие вопрос решение ответ. Быстро и правильно считать. Правильно записывать решение задачи. Кричать и сердиться, когда ...«Олимпийский» задачник по математике
Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи — решайте их Д. Пойа. Если мы действительно что-то ...Графические приемы решения задач с параметрами
Решение уравнений и неравенств, содержащих параметры, является одним из самых трудных разделов элементарной математики. Для их решения обычно требуются ...«Задачи по математике»
Успех каждого – это шаг к успеху всего класса. Реши примеры 5 ·8 5·5 4·6 8·8 25-5 36-6. 48-8 99-9 6·10 50·10 4·10 7·100. =40 =25 =24 =64 =20 =90 =60 ...Авторские задачи по математике и физике, составленные по повести Н.В. Гоголя «Ночь перед Рождеством
Методологическая основа: Класс арифметических задач огромен. Учащиеся старших классов обычно пытаются решать такие задачи алгебраически, так как владеют ...Вычитание. Решение задач с помощью действия вычитания
Определение целей урока. Чему должны научиться сегодня на уроке? Какими свойствами вычитания будем пользоваться? Что нужно будет знать, чтобы решить ...Геометрическая экскурсия по теме "Круглые тела в архитектуре"
Павловское начато строиться в 1777 году. Круг в Древней Греции считался венцом совершенства. Возможно, для того чтобы подчеркнуть совершенство природы ...Бинарный урок математики и природоведения по теме "Итоговое повторение"
Итоговое повторение. Ну-ка, проверь дружок, Ты готов начать урок? Всё ль на месте, Всё ль в порядке, Ручка, книжка и тетрадка? Все ли правильно сидят? ...Веселые задачки по математике
Задача 1. Попугай, удав и мартышка вместе съели 50 бананов. Попугай съел 3 банана. Сколько процентов всех бананов съел попугай? Задача 1. Решение. ...Алгоритм решения простых задач
. ЗАДАЧА условие Вопрос, задание. Работа в парах. 1. Налетело 5 гусей-лебедей, подхватили и унесли братца Иванушку. 2. Печка испекла девять ржаных ...Башни Кремля. Задачи по математике
Башни Кремля. Спасская башня считается самой красивой и стройной башней. Построена в 1491 году под руководством архитектора Пьетро Антонио Солари ...Викторина по математике в 7 классе
14 декабря 2012г. Цели викторины: развивать логическое мышление учащихся; закрепить знания полученные на уроках математики; развивать умение быстро ...Авторалли по городам математики
Цель: Закрепить навык выполнения действий, возведения чисел в квадрат и куб, закрепить формулы пути и площади. Расширение кругозора учащихся, развитие ...ГИА-2012. Решение планиметрических задач на нахождение углов геометрических фигур
1 3 4 5 6 7 8 9 10 11. Вашему вниманию представлено двенадцать прототипов задачи № 11 Открытого банка заданий по математике. ГИА – 2012. Два острых ...Аксиомы стереометрии Решение задач
Через любые две точки пространства проходит единственная прямая. Через любые три точки пространства, не принадлежащие одной прямой, проходит единственная ...ВПР по математике
Цель:. Познакомить уч-ся с подробным разбором заданий ВПР по математике ; Развивать мышление и логику учащихся. Выявить задания, вызывающие наибольшие ...Внеклассное мероприятие по математике для учащихся 6 -ов
Цель внеклассного мероприятия:. 1. Повышение интереса к изучению математики, развитие творческих способностей учащихся и логического мышления. 2. ...Конспекты
Дополнение условия задачи. Решение задач
Конспект урока по математике для 1 класса по УМК 21 век. ТЕМА. :. «Дополнение условия задачи. Решение задач». ЦЕЛИ:. 1. Учить выделять части задачи, ...Деление и умножение на однозначное число. Решение задач с использованием экологических понятий и терминов
Полякова Елена Александровна. учитель начальных классов. НОУ «Школа – интернат №8 ОАО «РЖД». УРОК . МАТЕМАТИКИ. (3. класс). Тема. : «. ...Диаграммы. Решение задач
Автор (фамилия, имя, отчество полностью) загружаемого материла. . . Гиль Наталья Николаевна. . . Место работы (полное наименование ОУ, город, ...Деление с остатком. Решение задач на деление с остатком
. Урок математики. . «Деление с остатком. Решение задач на деление с остатком». . Учитель:. Московченко Е. Н. ...Деление с остатком. Решение задач
Урок математики в 3 классе по теме. «Деление с остатком. Решение задач». . Учитель начальных классов. МОУ «СОШ № 8» г.Саранск. Клёмина Татьяна ...Деление на группы по несколько предметов
Технологическая карта урока. Учитель:. Панюкова Ольга Васильевна. . Класс. . . 1. . . . Предмет:. . Математика. . . ...Вычисление по формулам
Полная разработка открытого урока по математике в 6 классе "Вычисление по формулам". Урок соответсвует ФГОС. Разработка включает в себя конспект урока, ...Животноводство в нашем крае. Решение задач на движение
Муниципальное общеобразовательное учреждение. «Туендатская основная общеобразовательная школа». Первомайского района Томской области. ...Действия с составными именованными числами. Решение задач различного вида
Урок математики в 4 классе. . По программе «Школа 2100». Тема урока:. “Действия с составными именованными числами. Решение задач различного вида. ...Действия с величинами. Соотношение цены, количества, стоимости. Решение задач, выражений
Автор: Енина Н.В. учитель начальных классов МКОУ НОШ №17 ст.Зольской,. . Ставропольский край. . Урок математики в 3-м классе. УМК «Гармония». ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Математика
Автор презентации:Богдановской В.М.
Содержит:14 слайд(ов)
Поделись с друзьями:
Скачать презентацию