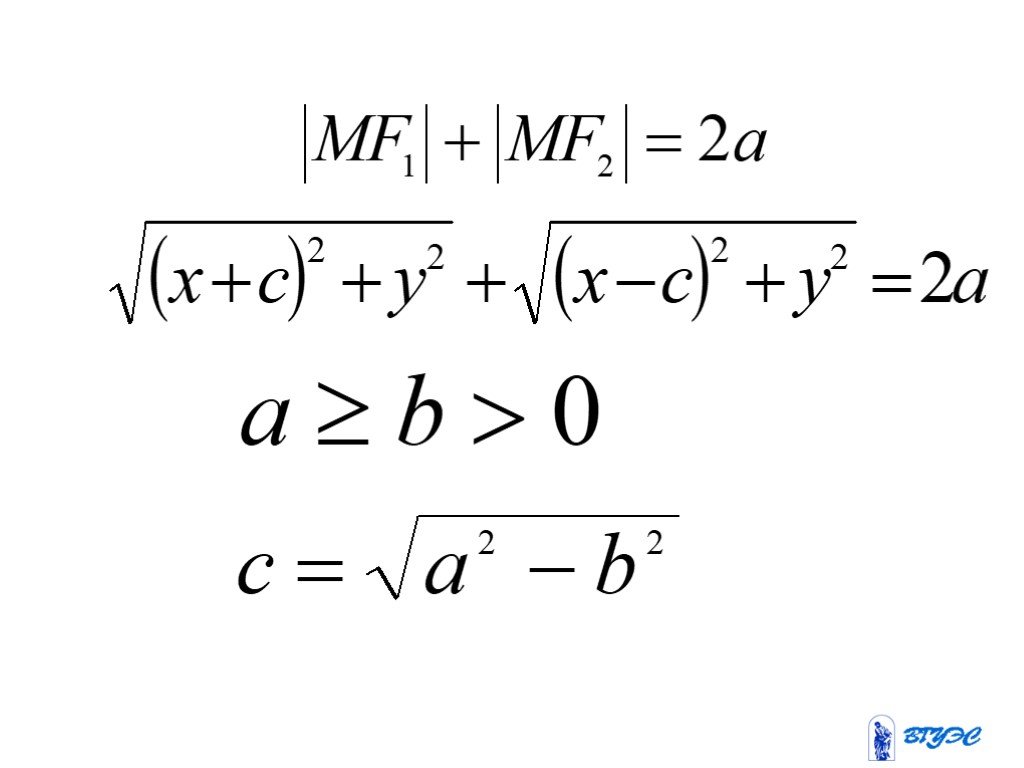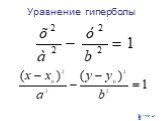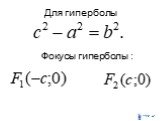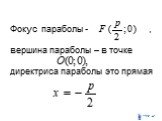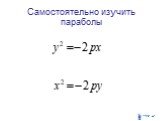Презентация "Кривые второгопорядка" по математике – проект, доклад
Презентацию на тему "Кривые второгопорядка" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 39 слайд(ов).
Слайды презентации
Список похожих презентаций
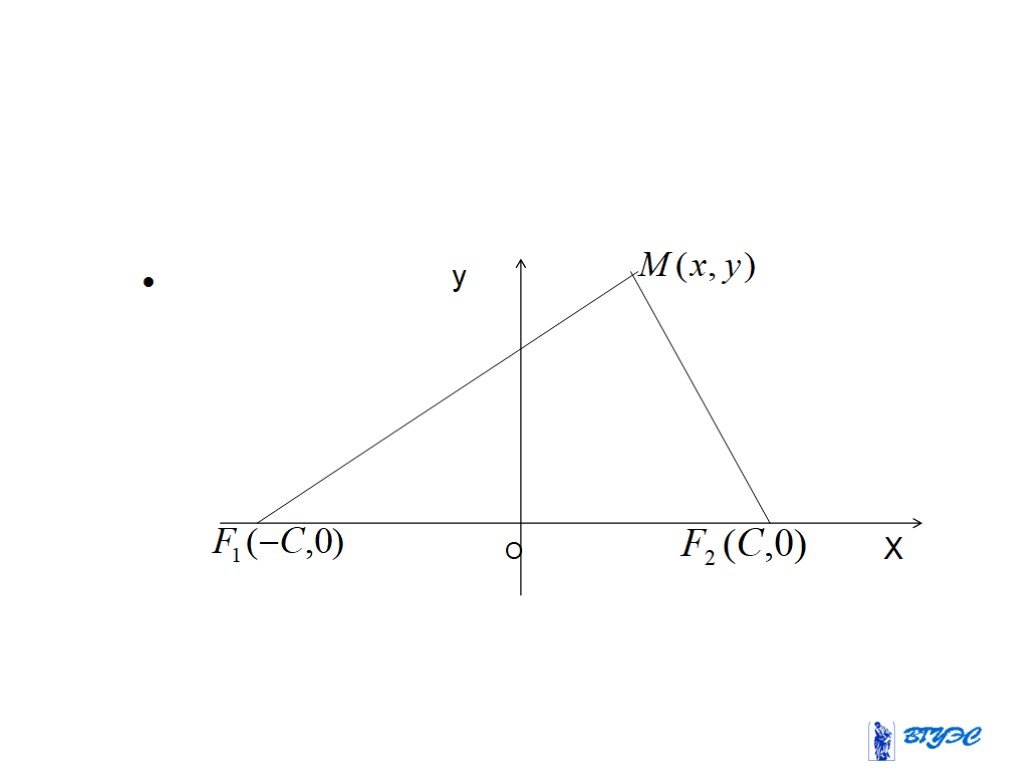
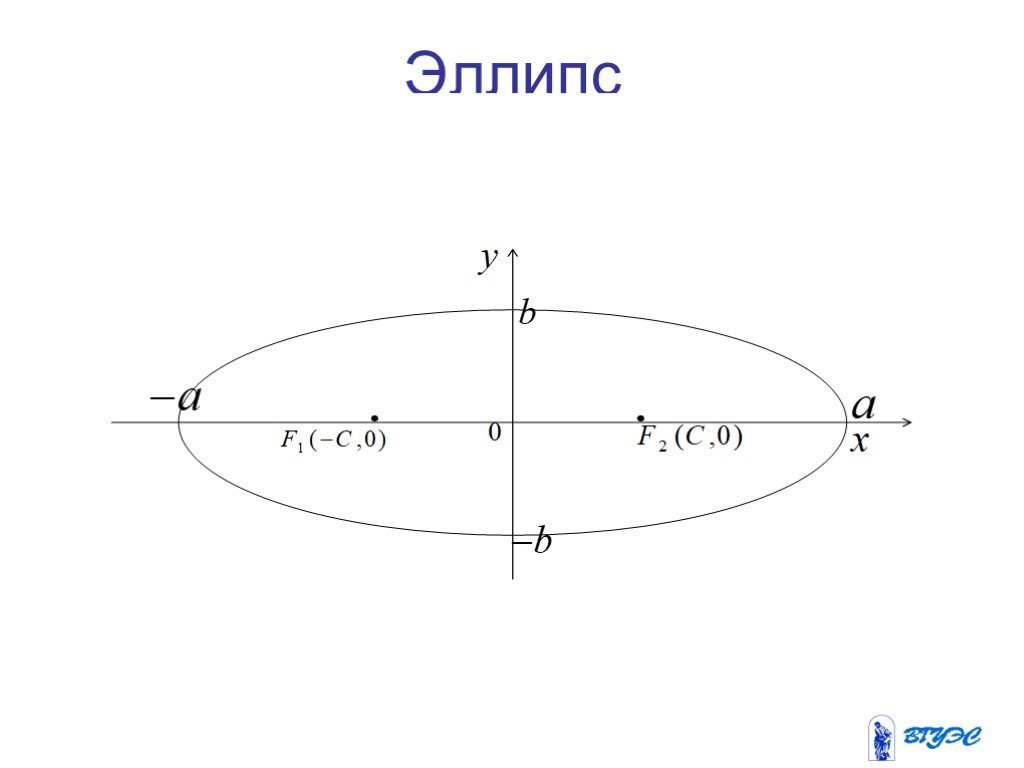
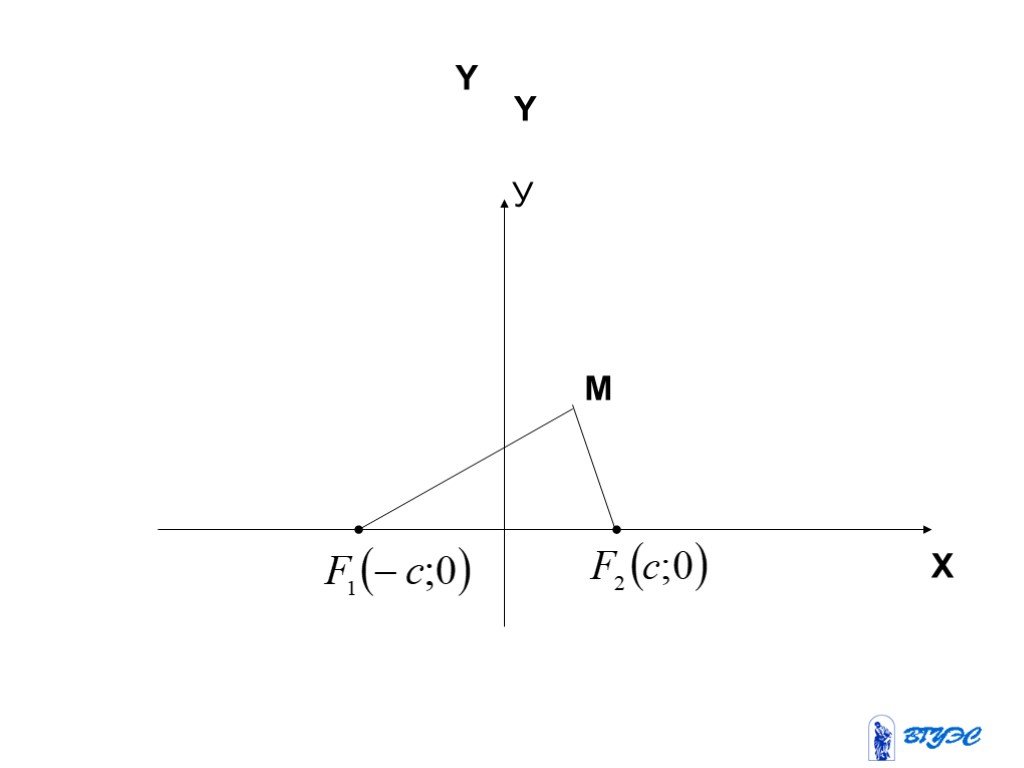
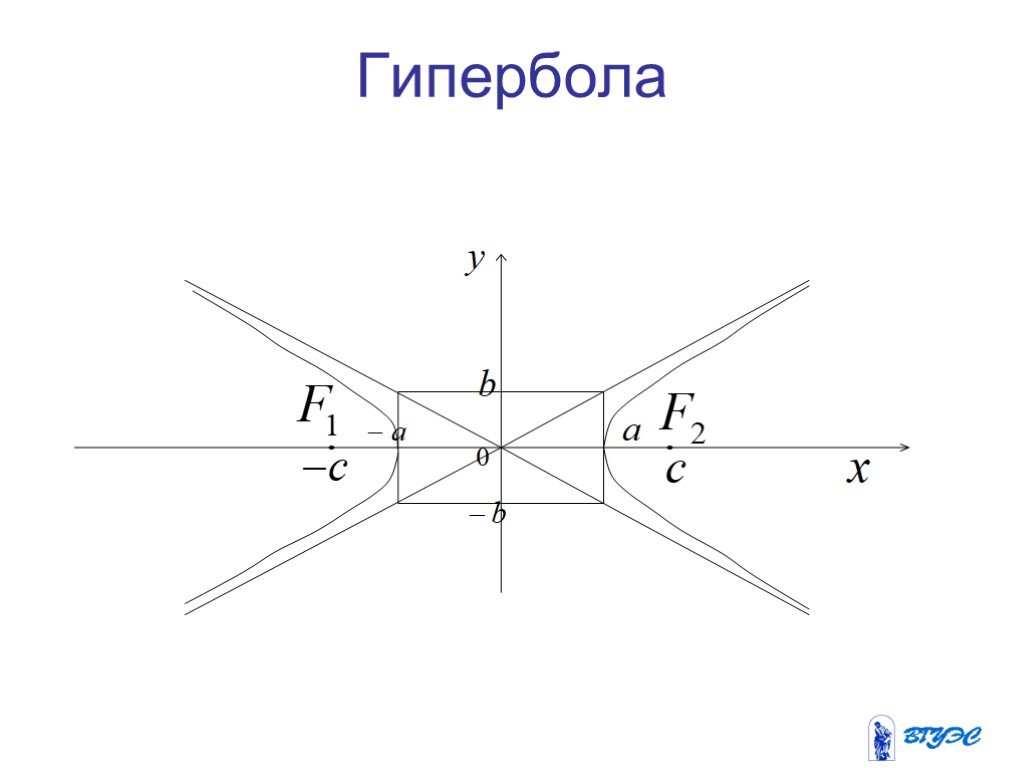
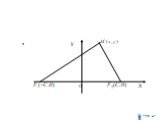
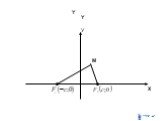
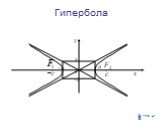
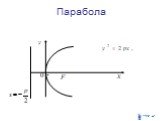
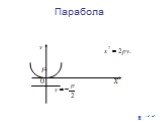
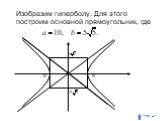
Кривые второго порядка
Цели и задачи. Цели: Рассмотреть основные понятия по теме «Кривые второго порядка» Задачи: Рассмотреть понятие кривой второго порядка Исследовать ...Занимательная математика
Внеклассное мероприятие по математике. Михаил Юрьевич Лермонтов. Автор: Лазарева Ирина Владимировна Учитель математики, г. Москва, ГБОУ ЦСиО «Самбо-70» ...Занимательная математика
На день какого святого наши предки имели обычай отдавать своих детей в учение? Чтобы ответить на вопрос, выполните действия и составьте слово, расположив ...Занимательная математика
Задачи: Закрепление умений и навыков, полученных на уроках математики. Расширение кругозора учащихся. Привитие интереса к математике. Цели урока: ...Занимательная и информатика и математика для начальной школы
Постановка задачи: Разработка Интернет ресурса, содержащего комплекты иллюстрированных заданий и филвордов. Особенности разработки: 1. Поиск занимательных ...Куда пропала математика?
Замочек №1. Задача 1. Часто знает и дошкольник, Что такое треугольник. А уж вам-то как не знать! Но совсем другое дело: Очень быстро и умело Треугольники ...Интересная математика
Франция Герб Франции Флаг Франции. . Страна граничит с 8 странами: Италией, Испанией, Бельгией, Люксембургом, Германией, Швейцарией, Монако и Андоррой. ...Занимательная математика для
23 х 25 = 7)42 + 22 = 54 : 5= 8)52 +14 = 119 = 9)62 – 23 = 291 = 10)102 – 92 = 42 = 52 =. I. Немного по теме. II. Задачи без возраста. Задача 1. Четверо ...Арифметические действия над числами или зачем туристу математика?
27 сентября – день туриста. 34 х 2 = 90 : 30 = 9 + 45 = 11 х 3 = 80 – 19 = 55 : 5 = И У Р Т С 68 3 54 33 61 11. Что лежит в рюкзаке туриста? спички ...«Устный счёт» математика
1- 0,4 3 +2,4 3,2 – 2 3,2- 0,2 12,3 + 3,4 2,04 + 3,6 12 – 1,5 6,2- 2,6 ( 12,4 + 3,67)- 2,67 ( 45,06 + 23,5) – 40 ,06. 0,6 5,4 1,2 3 15,7 5,64 10,5 ...«Углы» математика
Цель урока:. познакомить учащихся с геометрической фигурой углом, с видами углов (прямой, тупой, острый), сформировать представления о существенных ...«Своя игра» математика
Математическая игра-викторина «Своя игра». Конец игры Литература. Задачи – шутки 50. Вопрос: Один господин написал о себе: «Пальцев у меня двадцать ...«Своя игра» математика
Условия игры:. Участники сами выбирают темы и вопросы. Вопрос выбирает правильно ответившая команда. 210 – 250 баллов – отметка «5». 110 -200 баллов ...«Координатная плоскость» математика
Цели и задачи урока:. 1. Ввести понятие координатной плоскости, уметь определять координаты точек, строить точки по их координатам. 2. Развивать мышление, ...Занимательная математика
Хочу стать фокусником…. Искусство отгадывать числа. Есть фокус по отгадыванию чисел: «фокусник» просит вас складывать, умножать, вычитать задуманное ...Занимательная математика
Добрый день! Приветствую вас, мои юные друзья математики. Удачи вам! Ваш друг Математик. Славянская кириллическая десятеричная алфавитная нумерация. ...береза глазами математика
Цель. Целью данного исследования является выявление в повседневной жизни различных законов, которым нас обучают еще в школе. И как же все можно связать ...Занимательная математика Думай, считай, отгадывай!
г.Санкт-Петербург. Ростральная колонна. телевизионная башня. Исаакиевский собор. Зимний дворец. Нева. а) Высота Ростральных колонн (в метрах). б) ...Веселая математика
1. Разминка «Веселый урок». 2. Конкурс художников. Нарисуйте фигуры, не отрывая карандаша от бумаги и не проводя дважды по одной и той же линии. 3. ...Конкурсный урок математика
У Ромы не «3», а у Лены не «3» и не «5». Кто какую отметку получил? Проверь себя! 4 5. Запомни! . . Какую из этих схем составила Таня? I способ: 90 ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:13 июня 2019
Категория:Математика
Содержит:39 слайд(ов)
Поделись с друзьями:
Скачать презентацию