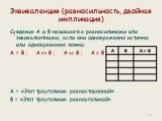
Презентация "Алгебра суждений" (6 класс) по информатике – проект, доклад
Презентацию на тему "Алгебра суждений" (6 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Информатика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 12 слайд(ов).
Слайды презентации
Список похожих презентаций
Алгебра логики Логические операции
Логика. Логика – это наука о формах и законах человеческой мысли, о законах доказательных рассуждений, изучающая методы доказательств и опровержений, ...Алгебра логики Логическое умножение, сложение и отрицание
Алгебра высказываний. Алгебра высказываний была разработана для того, чтобы можно было определять истинность или ложность составных высказываний, ...Алгебра логики вторая часть
Мышление. Логика – наука о формах и способах мышления. Основные формы мышления – понятие, высказывание, умозаключение. Понятие – форма мышления, фиксирующая ...Алгебра логики
Еще живший в 384 - 322 г.г. до нашей эры древнегреческий ученый и философ Аристотель (Ἀριστοτέλης) пытался найти ответ на вопрос “Как мы рассуждаем”, ...Алгебра логики
Понятие- это форма человеческого мышления, где фиксируются основные, существенные признаки объекта. Любое понятие состоит из двух составляющих: объёма ...Алгебра логики первая часть
Логика - это наука о формах и способах мышления. Понятие; Высказывание; Умозаключение. Основные формы мышления:. это форма мышления, фиксирующая основные, ...Алгебра логики
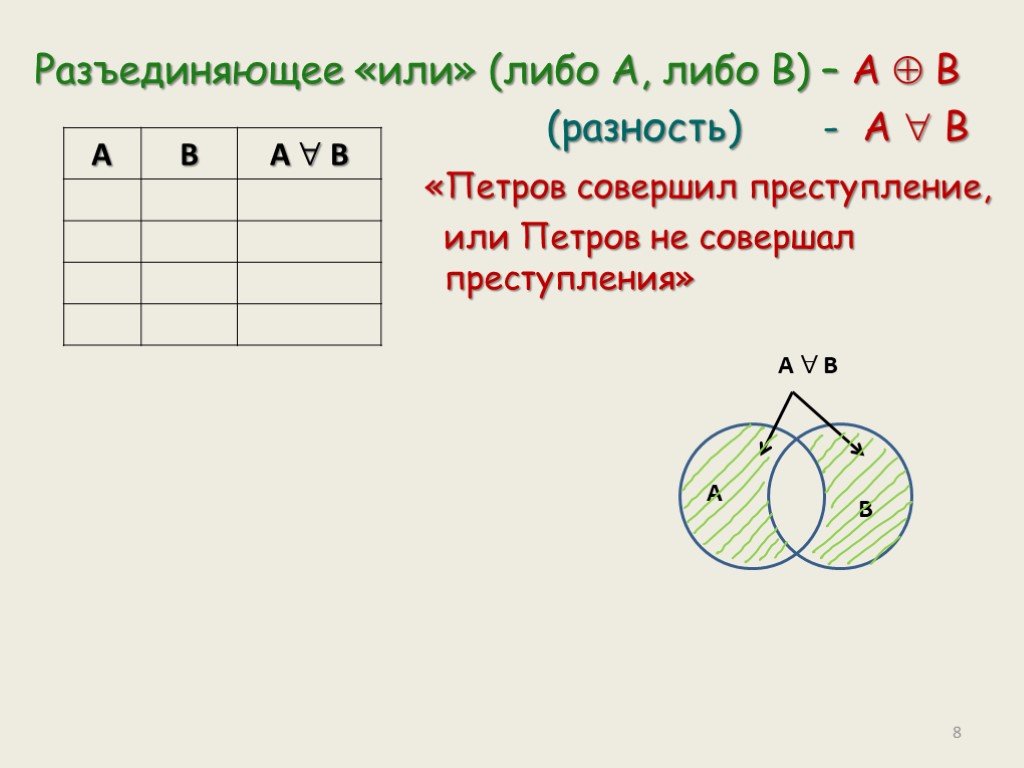
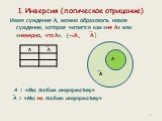
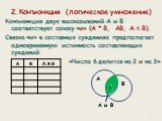
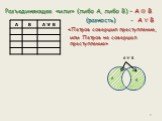
Функции алгебры логики (булевы функции). . Основные законы алгебры логики. 1) Законы нулевого множества. 2) Законы универсального множества. 3) Законы ...Алгебра логики
Содержание. Алгебра логики Логическое высказывание Простое и сложное высказывания Основные логические связки Основные логические операции Триггер ...Алгоритмизация и программирование в Pascal
Вводная часть. Процесс решения задачи на ПК – это совместная деятельность человека и машины. Его условно можно разделить на несколько этапов. Человеку ...Тест Алгоритмизация и программирование
В этой презентации приводятся тренировочные задания из нескольких источников: открытого сегмента федерального банка тестовых заданий, демонстрационных ...Фрагментированное программирование
Цель работы. Распараллеливание исполнительной системы (ИС) фрагментированного программирования и её оптимизация. Постановка задачи. Разработка многопоточной ...Правовая информатика
Исполнение и цели. Правовая информатика – это междисциплинарная отрасль знания о закономерностях и особенностях информационных процессов в сфере юридической ...Социальная информатика
Социальная информатика - это наука, изучающая комплекс проблем, связанных с прохождением информационных процессов в социуме. Один из основоположников ...Основы логики и логические основы построения компьютера
Процессор компьютера выполняет арифметические и логические операции над двоичными кодами. И поэтому чтобы иметь представление об устройстве компьютера, ...Основы логики
ФОРМЫ МЫШЛЕНИЯ. Логика – это наука о формах и способах мышления. Это учение о способах рассуждения и доказательств. Мышление. Понятие – выделение ...Основы логики
Логика – это наука о формах и способах мышления. ОСНОВНЫЕ ПОНЯТИЯ: Д. Буль (1815-1864). Основные формы мышления. Понятие Умозаключение Высказывание. ...Объекты и их свойства информатика
Объект - ЯБЛОКО красное круглое вкусное висит съедается продается зеленое кислое. о нем рассказывают. Объект - КНИГА листать читать. закрывать закладывать. ...Алгоритмизация и программирование
Исполнители алгоритмов. КАЛЬКУЛЯТОР 1. У исполнителя Калькулятор две команды, которым присвоены номера: вычти 1; умножь на 3. Первая из них уменьшает ...Основы логики
Алгебра логики (булева алгебра) - это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ...Алгоритмы и программирование
АЛГОРИТМ Линейный Циклический С ветвлением С процедурой. Программа – запись алгоритма на языке программирования для компьютера. Алфавит языка. Алфавит ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 апреля 2019
Категория:Информатика
Классы:
Содержит:12 слайд(ов)
Поделись с друзьями:
Скачать презентацию