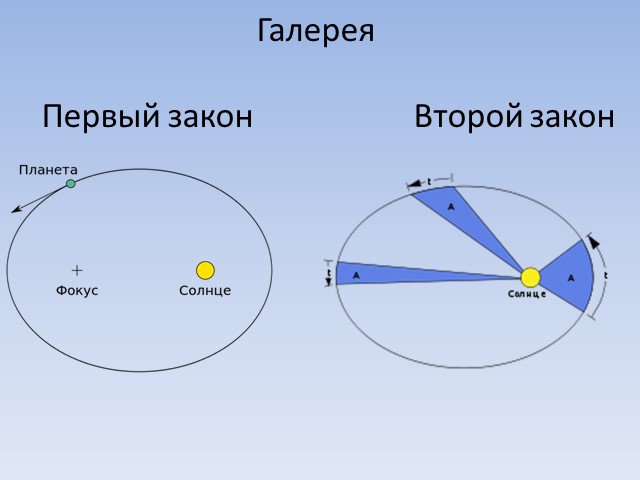
Презентация "Законы Кеплера" (11 класс) по физике – проект, доклад
Презентацию на тему "Законы Кеплера" (11 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 12 слайд(ов).
Слайды презентации
Список похожих презентаций
Законы постоянного тока
Элементы содержания, проверяемые на ЕГЭ 2010: Электрический ток. Сила тока, напряжение, электрическое сопротивление Закон Ома для участка цепи Электродвижущая ...Законы постоянного тока. Энергия конденсаторов
Закон сохранения электрического заряда. Справедлив для замкнутой системы зарядов. Сумма зарядов алгебраическая, то есть с учетом знаков зарядов. Конденсатор ...Фотоэффект. Законы фотоэффекта
Завершение классической физики. В конце XIX в. многие ученые считали, что развитие физики завершилось по следующим причинам: 1. Больше 200 лет существуют ...Законы постоянного тока
ТЕМА УРОКА. ЗАКОНЫ ПОСТОЯННОГО ТОКА. Цель урока. Поставим пред собою цель, Чтоб после этого урока Мог каждый другу рассказать Как вычислить сопротивление, ...Законы термодинамики
НУЛЕВОЕ НАЧАЛО ТЕРМОДИНАМИКИ. Нулевое начало термодинамики сформулированное всего около 50 лет назад , по существу представляет собой полученное «задним ...Оптика. Законы отражения и преломления света. Линзы. Построение изображения в линзах
Свет – электромагнитное излучение, воспринимаемое глазом. Геометрическая оптика- раздел оптики, изучающий законы распространения световой энергии ...Законы Кирхгофа
Густав Роберт Кирхгоф (1824-1887). Gustav Robert Kirchhoff Немецкий физик, один из великих физиков XIX века. Законы кирхгофа. Зако́ны Кирхго́фа — ...Законы сохранения
Содержание:. Закон Сохранения Импульса Закон Сохранения Механической Энергии Работа и Энергия. Закон Сохранения Импульса. Импульсом называют векторную ...Законы движения тел
1. Можно ли считать материальной точкой поезд при определении: пути, который он проехал а) за 2 ч;. 2. Можно ли считать бревно плывущее по реке за ...Законы идеальных газов
ГАЗОВЫЕ ЗАКОНЫ (10 класс). Цели урока. 1.Способствовать формированию у учащихся знания молекулярно-кинетической теории идеального газа; выявить причинно-следственные ...Законы геометрической оптики
Содержание: Кроссворд.Прочитайте пословицу и ответьте на вопросы.
Решаем задачи.
Какая картинка лишняя. 1). Область пространства, в которую свет ...
Законы газов
. Материя Вещество Поле. Состояния вещества:. Твердое Жидкое Газ Плазма. Электрическое Магнитное Гравитационное Торсионное Биологическое Информационное. ...Законы волновой оптики
Волновая оптика Развитие представлений о природе света Первые представления о природе света возникли у древних греков и египтян. По мере изобретения ...Законы преломления
Преломление света Примеры явления . При переходе из одной среды в другую световые лучи меняют свое направление. Наблюдается кажущееся изменение размеров ...Законы механики
Физика и реальность. Физика – это наука о природных явлениях. Физика изучает законы природы. Методы физики: наблюдение, эксперимент, теория, практика. ...Законы распространения света
Тема урока: «Отражение и преломление света». Закон отражения света:. Падающий луч Отражённый луч Перпендикуляр Угол падения Угол отражения. Граница ...Законы механики Ньютона
Введение. Кинематика позволяет определить вид движения, но не объясняет почему тело движется так, а не иначе? Опыты и наблюдения показывают, что:. ...Законы сохранения в механике
Импульс тела. Импульс тела - векторная величина равная произведению массы тела на его скорость. P=m v P (кг м /с). Примеры реактивного движения: полет ...Законы молекулярной физики
объясняет тепловые явления и свойства тел с точки зрения внутреннего строения вещества. МКТ молекулярно-кинетическая теория. Основные положения МКТ. ...Законы фотоэффекта
Домашнее задание. Г.Н.Степанова, Физика 11(1), § 22,23 Знать: Способы наблюдения фотоэффекта, Физическую суть явления, Цель опытов А.Г.Столетова, ...Конспекты
Отражение света. Законы отражения. Плоское зеркало
Урок по физике в 8 классе. «Отражение света. Законы отражения. Плоское зеркало». . ЦЕЛИ УРОКА. :. 1.ОБРАЗОВАТЕЛЬНА. Я – способствовать формированию ...Законы Кирхгофа
Тема. «Законы Кирхгофа». Цель:. . 1. . Изучить законы Кирхгофа; рассмотреть их назначение;. 2. Научить применять законы Кирхгофа для расчета ...Законы термодинамики
Урок рок физики по теме " Законы термодинамики". . Познавательные цели и задачи урока. Повторить и закрепить понятия: внутренняя энергия, тепловое ...Корпускулярно-волновой дуализм. Гипотеза де Бройля о волновых свойствах частиц. Соотношение неопределённостей Гейзенберга. Законы отражения и преломления света; поляризация, дисперсия света
Урок № 56-169 Корпускулярно-волновой дуализм. Гипотеза де Бройля о волновых свойствах частиц. Соотношение неопределённостей Гейзенберга. Законы отражения ...Законы сохранения в механике
"Законы сохранения в механике". . Урок физики в 10-м классе. . Тип занятия:. Семинар. Урок комплексного применения знаний. Продолжительность ...Законы сохранения в механике
Повторительно - обобщающий урок. Решение задач по теме «Законы сохранения в механике». Урок проводится в 10 классе при обобщающем повторении темы ...Законы Ньютона
Урок по физике 9 класс «Законы Ньютона» (повторение). Цель урока. :. создать условия для обобщения и закрепления знаний, полученных по теме ...Законы постоянного тока Урок-приглашение к эксперименту и рассуждениям
Северо-Казахстанская область. Акжарский район. Горьковская средняя школа. Жуманова Ж.Н. Урок физики. Тема:Законы постоянного тока. Урок-приглашение ...Законы Ньютона
. Урок в 10 классе. На уроке используется технология естественного обучения по методике д.п.н. . . Суртаевой Н.Н. . ТЕМА УРОКА. : Обобщение ...Законы Ньютона
Векленко Светлана Ильинична. . Приложение №5. Разработка урока в 9 классе по теме «Законы Ньютона». Предлагаемый урок физики проводится ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:19 июня 2015
Категория:Физика
Классы:
Содержит:12 слайд(ов)
Поделись с друзьями:
Скачать презентацию