Презентация "Потенциал, работа сил электростатического поля" по физике – проект, доклад
Презентацию на тему "Потенциал, работа сил электростатического поля" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 61 слайд(ов).
Слайды презентации
Список похожих презентаций
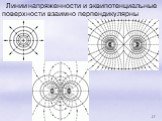
Напряжение электростатического поля
10. Электростатика. 10.1. Электрические заряды. Единица электрического заряда — кулон (Кл) — электрический заряд, проходящий через поперечное сечение ...Напряженность электростатического поля
Самостоятельная работа ( 3мин ). Вариант 1. Два точечных заряда величиной -3мКл и 4мКл притягиваются с силой 750 Н. На каком расстоянии находятся ...Потенциал поля
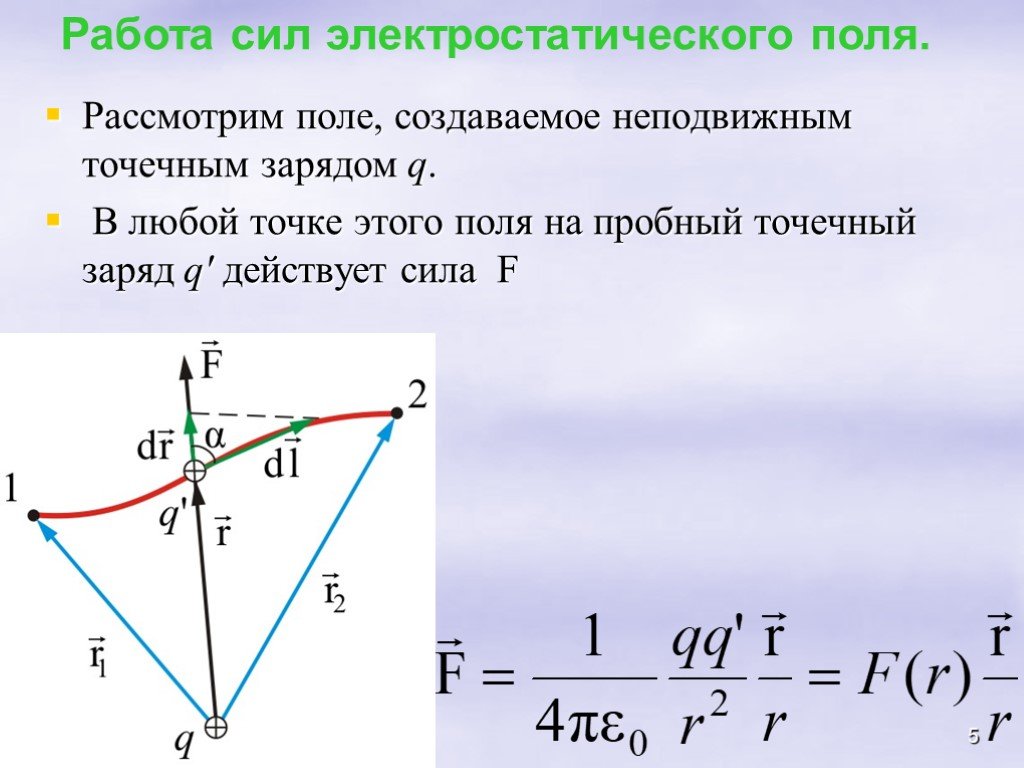
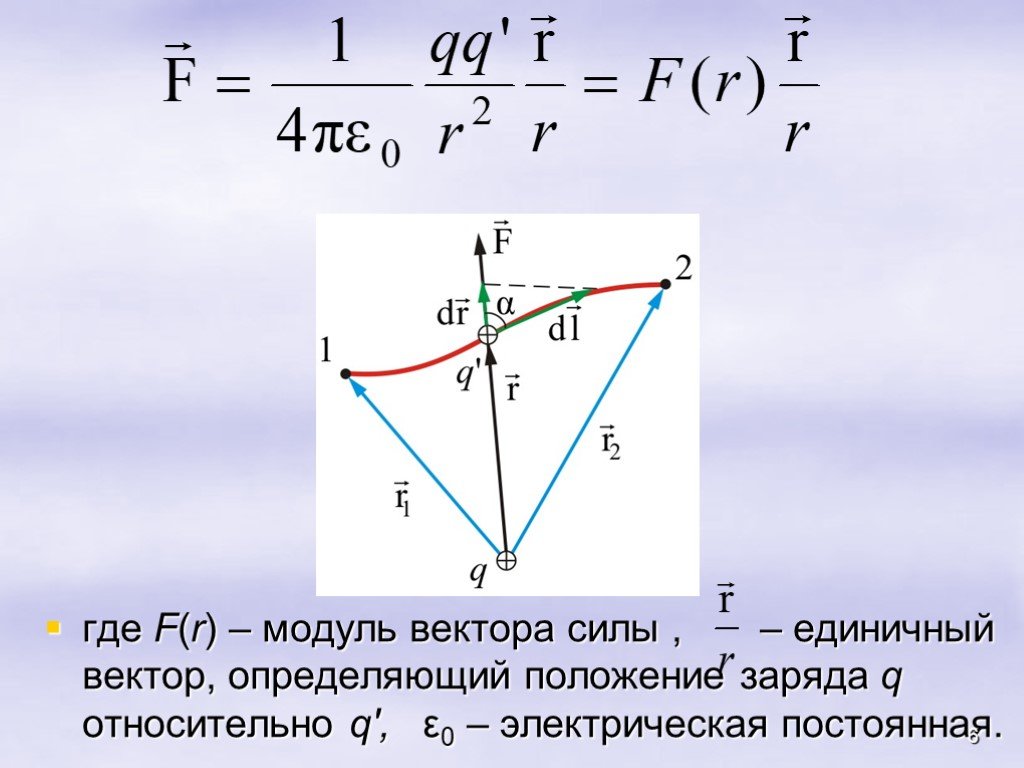
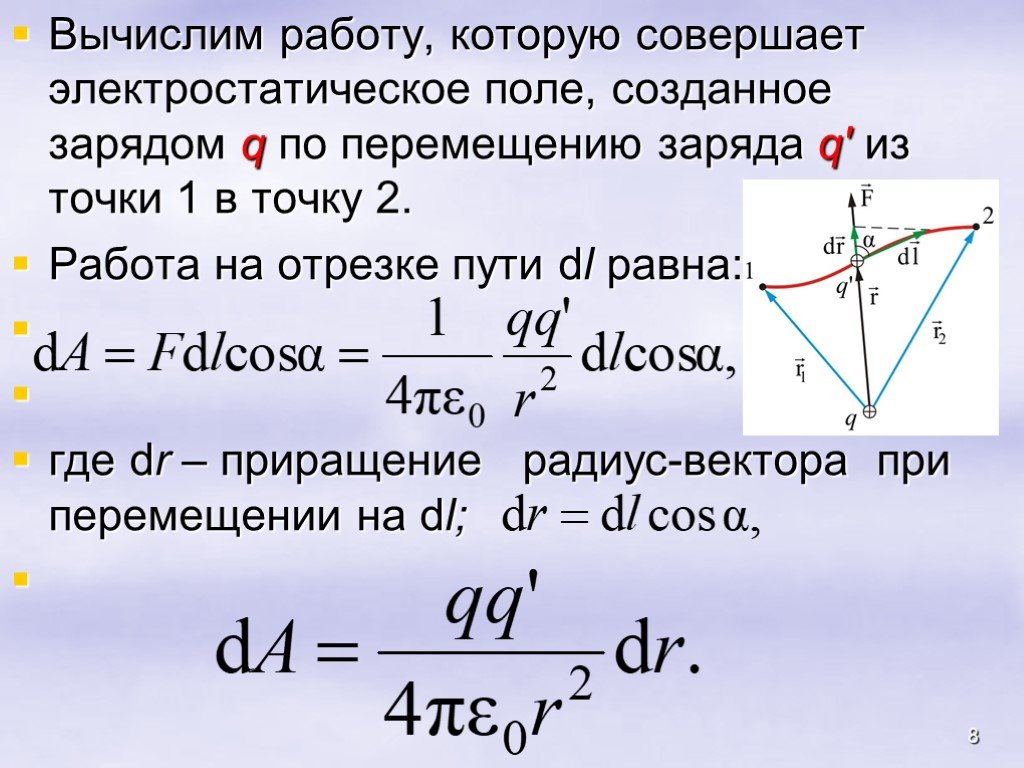
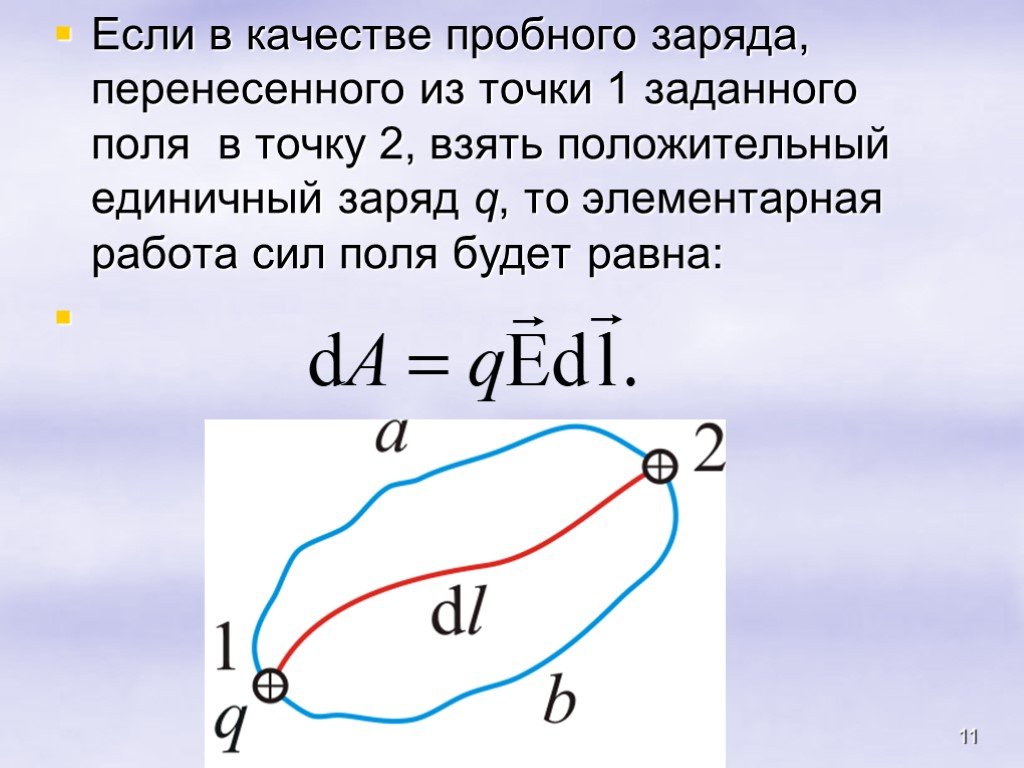
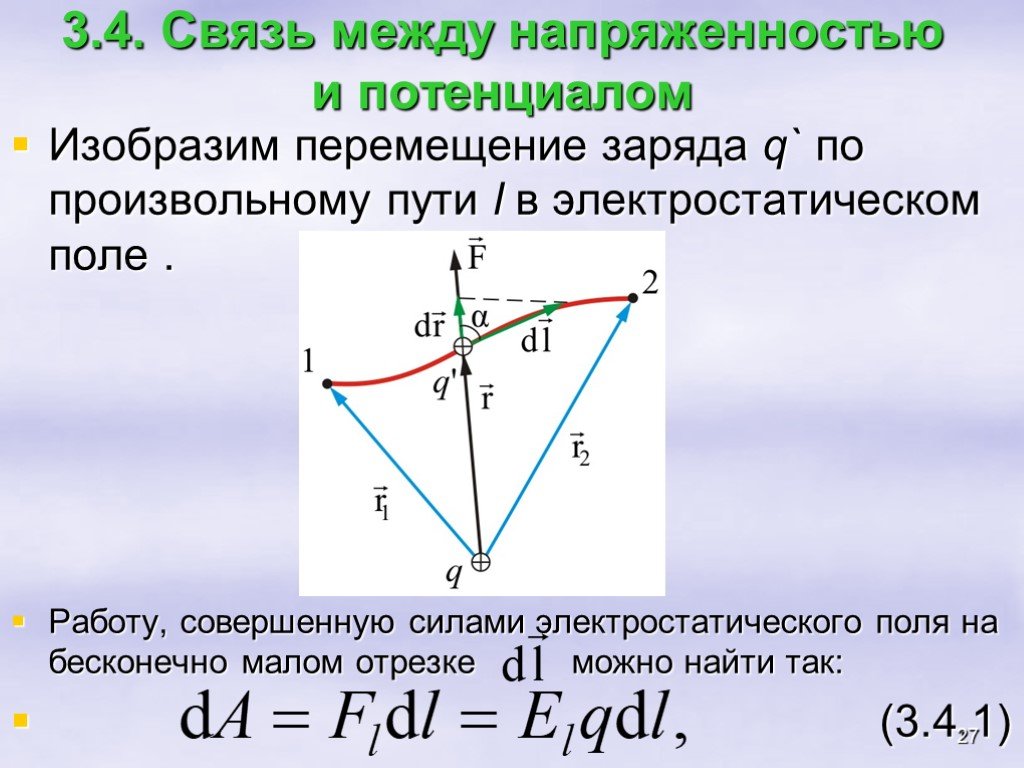
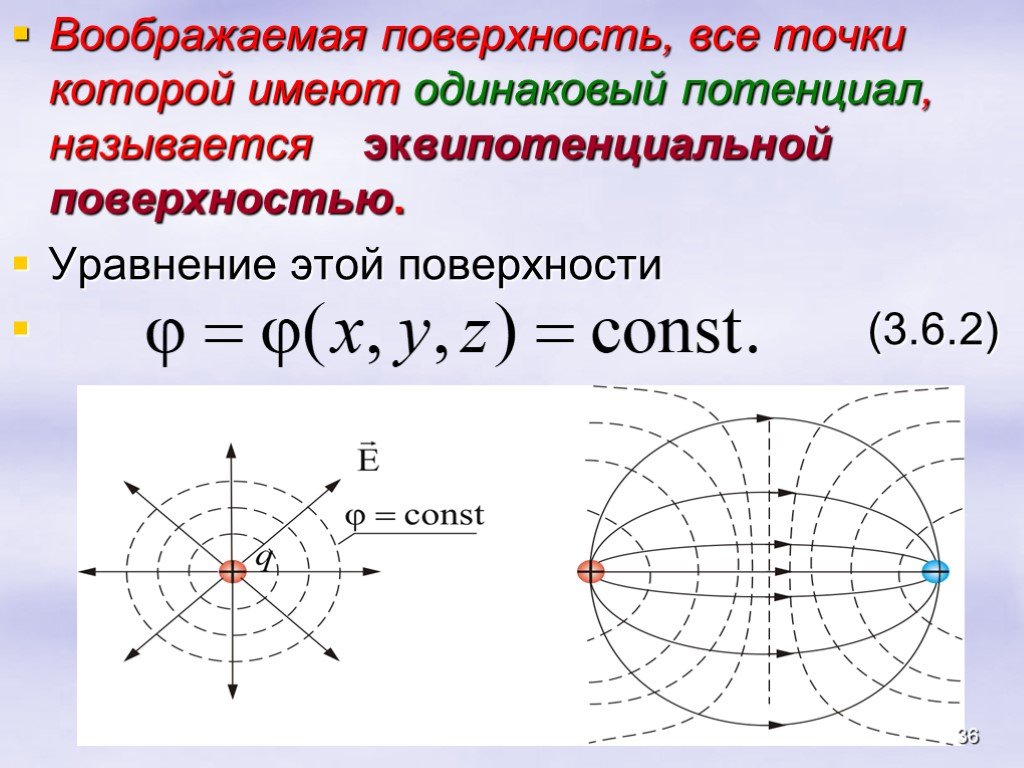
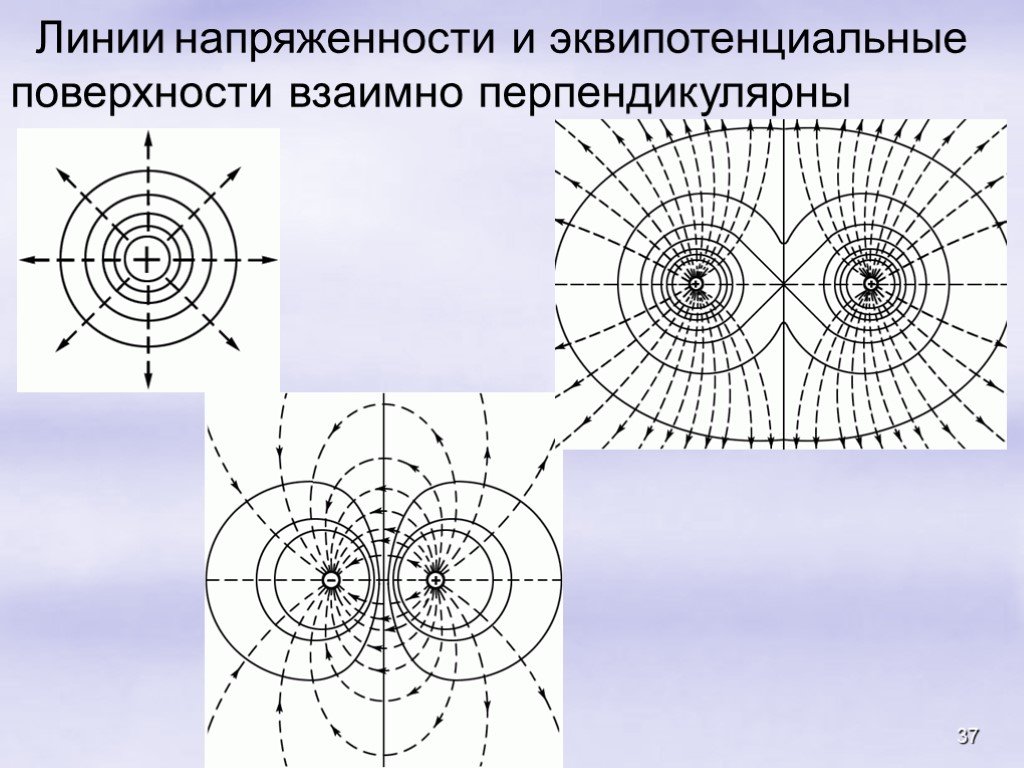
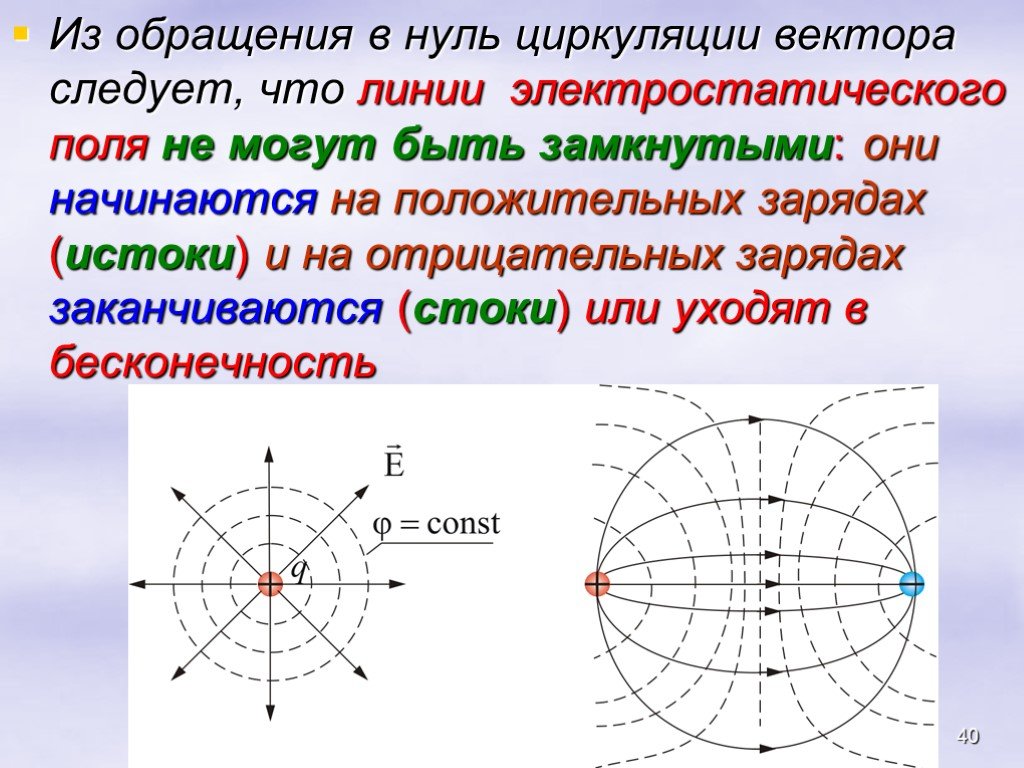
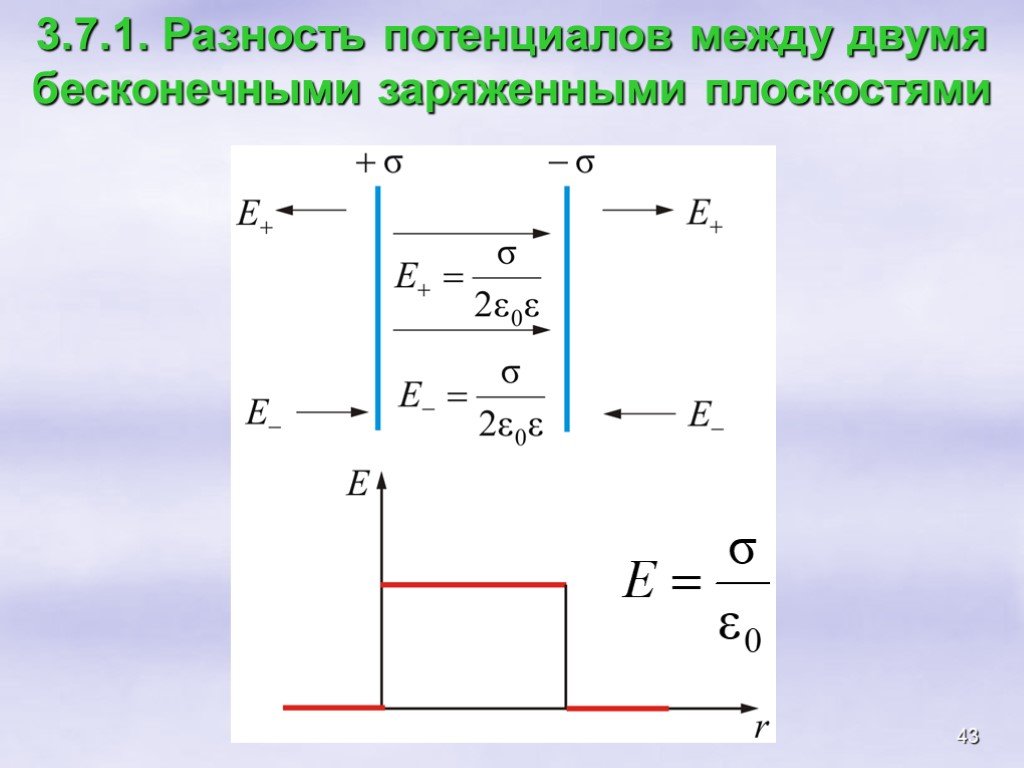
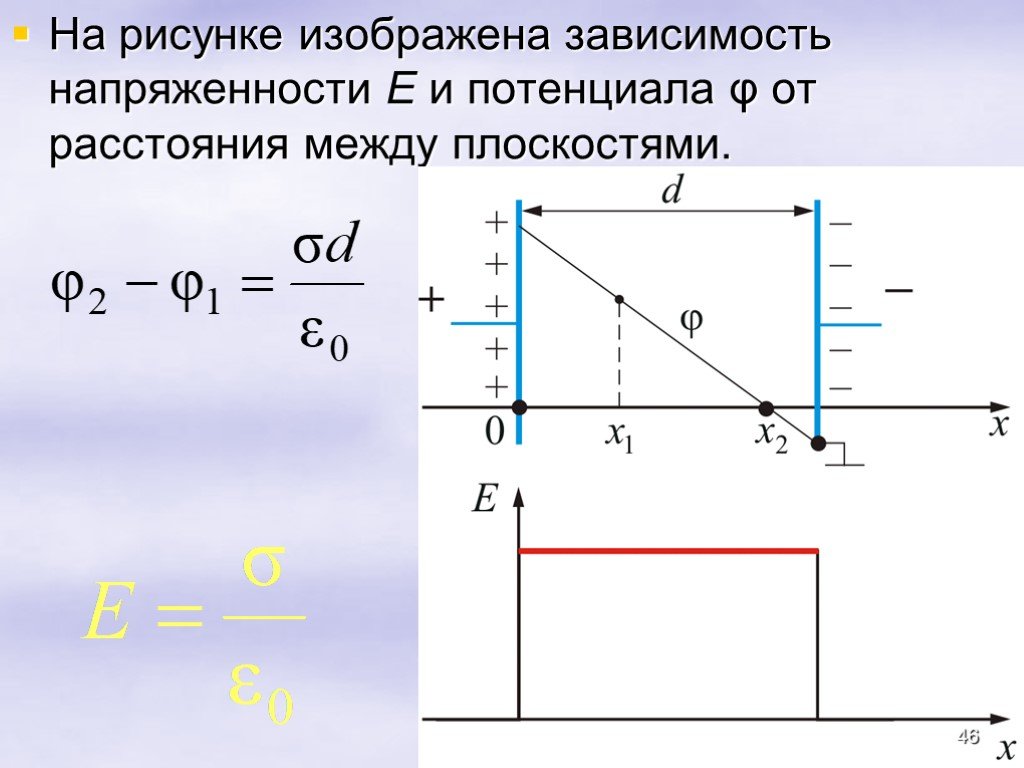
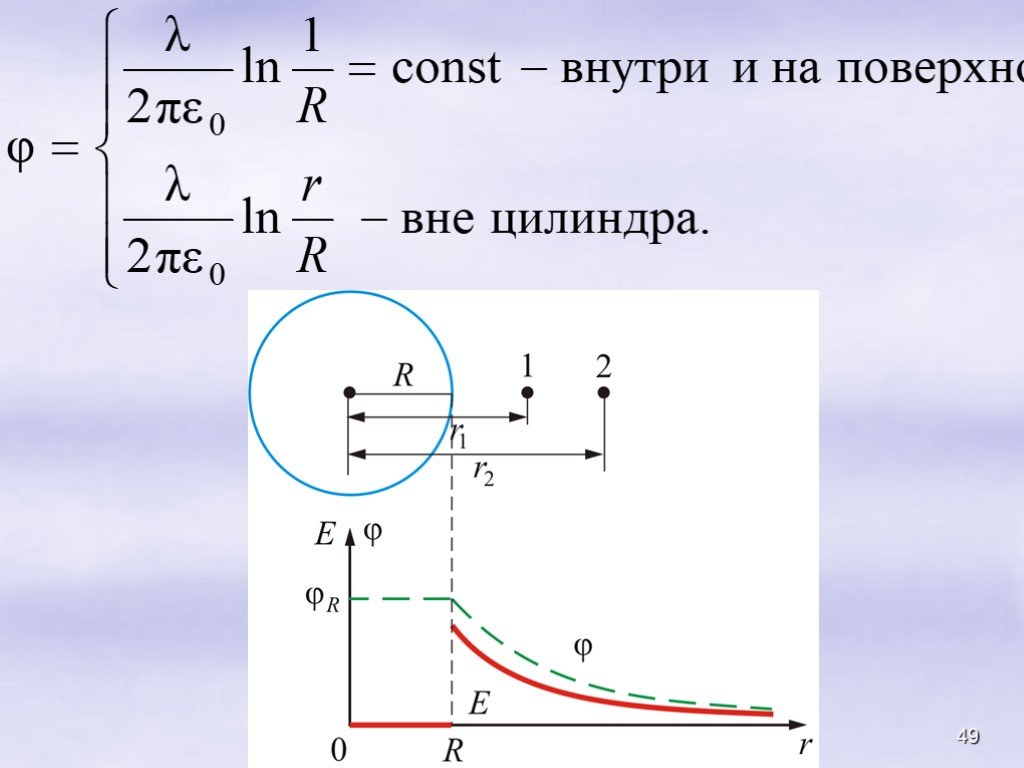
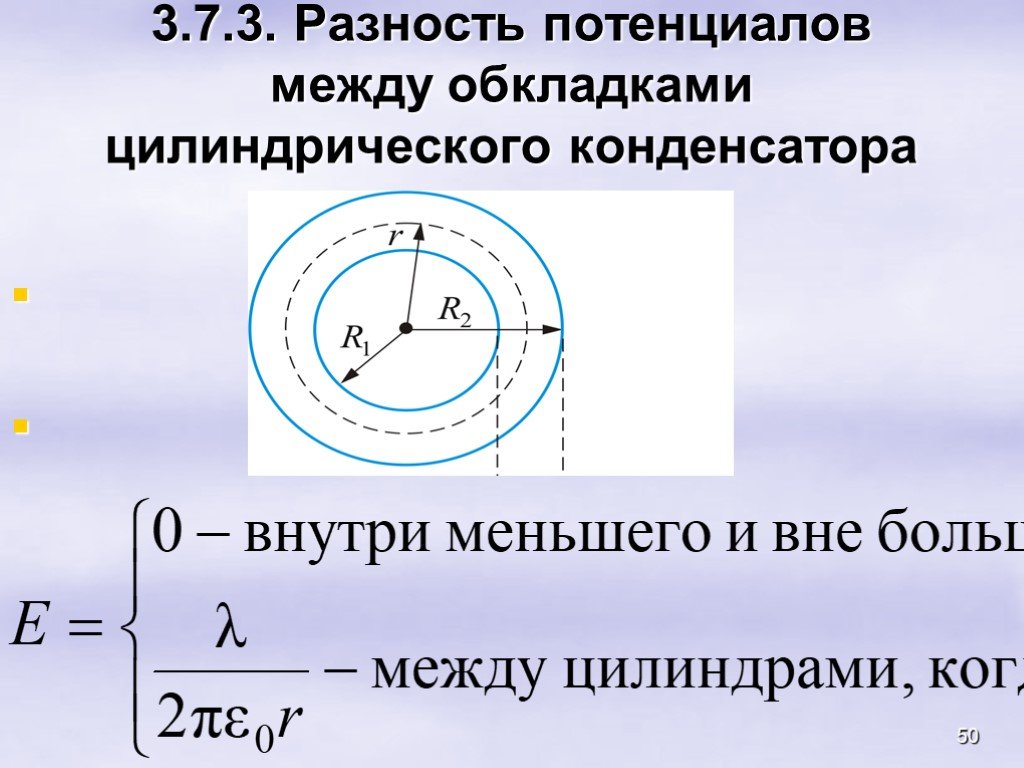
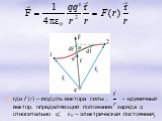
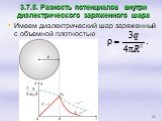
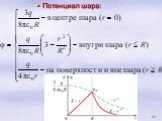
Всякое электростатическое поле-потенциально. (т.к. оно способно совершить работу по перемещению заряда). Свойства. Если поле совершает положительную ...Конденсатор-энергия электростатического поля
Чему равен суммарный заряд незаряженного проводника? Как размещается избыточный заряд на изолированном проводнике в отсутствие внешнего электростатического ...Самостоятельная работа
Вопрос 1. 1 вариант Два автомобиля движутся в одном и том же направлении со скоростями υ1 и υ2 относительно поверхности Земли. Чему равна скорость ...Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки
Тестовая работа. 1. Когда электрические заряды находятся в покое, то вокруг них обнаруживается… А. Электрическое поле. Б. Магнитное поле. В. электрическое ...Направление тока и направление линий его магнитного поля
Магнитное поле - это особый вид материи, невидимый и неосязаемый для человека, существующий независимо от нашего сознания. Магнитные линии. Магнитное ...Механическая работа и мощность
Цель урока: 1. Формирование у учащихся физических понятий «работа», «мощность». 2. Выяснение физического смысла механической работы. План урока: 1. ...Механическая работа и мощность
повторение основных понятий и формул, связанных с механической работой и мощностью, а также на примерах типовых задач в соответствии с кодификатором ...Механическая работа
ВЫВОД 1. Под действием силы тело перемещается. Вывод 2. Механическая работа совершается тогда, когда тело движется под действием силы. Вывод 3. Если ...виды сил
Каждый из нас постоянно встречается с различными случаями действия тел друг на друга. В результате взаимодействия скорость движения какого-либо тела ...Виды сил
Цели урока: обучения: развития: воспитания:. - систематизировать знания о силах природы; - совершенствовать умение решать экспериментальные, качественные ...Виды сил
Определение силы Сила тяжести Сила упругости Вес тела Сила трения Динамометр. Сила – количественная мера взаимодействия тел. Результат действия силы: ...Виды сил
Цель:. Повторить и обобщить знания по теме. Физический океан о.Тяготения о.Трения о.Упругости о.Веса. Силой называется физическая величина, которая ...Виды взаимодействий, сил в механике и их характеристика".
Цель урока. для учащихся: научиться определять вид силы по разным взаимодействиям тел , давать характеристику любой механической силы и систематизировать ...Вибрация. Акустические величины. Электромагнитные поля
План лекции. Вибрация. Гигиенические характеристики и нормирование вибраций Защита от вибраций. Акустические величины. Действие шума на организм человека. ...Лабораторная работа
Содержит коллекцию лабораторных работ, демонстраций, коротких экспериментов и работ физического практикума, соответствующую всем возможным образовательным ...Механическая работа
Помогите объяснить! В повседневной жизни словом «работа» мы называем любой полезный труд рабочего, учителя, ученика. Понятие работы в физике другое. ...Виды сил. Равнодействующая сила. Правила сложения сил
Исаак Ньютон (1643 -1727). Сила – мера взаимодействия тел. Единица силы – Ньютон (Н). Fтяж. Сила, с которой Земля притягивает все тела, находящиеся ...Механическая работа
Механическая работа. Единицы работы. Тренировочные задания. Тест I вариант II вариант. В обыденной жизни под словом «работа» мы называем различные ...Конспекты
Магнитное поле, его свойства. Магнитное поле постоянного электрического тока. Действие магнитного поля на проводник с током. Сила Ампера. Принцип действия электродвигателя
Урок № 42 – 169 Магнитное поле, его свойства. Магнитное поле постоянного электрического тока. Действие магнитного поля на проводник с током. Сила ...Действие магнитного поля на движущийся заряд. Сила Лоренца
Урок № 43-169 Действие магнитного поля на движущийся заряд. Сила Лоренца. Сила Лоренца - сила, действующая со стороны магнитного поля на движущуюся ...Простые механизмы. Рычаг. Равновесие сил на рычаге
Урок. Простые механизмы. Рычаг. Равновесие сил на рычаге. Тип урока. : изучение нового материала. . Цель урока. :. . Обеспечить усвоение ...Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки
Урок по теме: «Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки». Цели урока:. . I. Образовательные:. . ...Направление тока и направление линий его магнитного поля
Тутаев Владимир Александрович. Учитель физики и информатики МБОУ «Ромашкинская СОШ». . с. Ромашкино Курманаевского района Оренбургской области. ...Механическая работа
. Тема. «Механическая работа». . 7 класс. . . Номер урока. (в году/ в теме) - 51/1. Цель:. на уроке обучающиеся познакомятся с работой как ...Действие магнитного поля на движущиеся заряженные частицы
План-конспект урока. в 11 классе. по теме « Действие магнитного поля на движущиеся заряженные частицы». тип урока. : комбинированный. методы:. ...Электрическая емкость. Конденсатор. Энергия электрического поля конденсатора
№__________сабақтың жоспары. План урока №___________________. Сабақтың тақырыбы:. . Тема урока. :. Электрическая емкость. Конденсатор. Энергия ...Самоиндукция. Индуктивность. Энергия магнитного поля тока
Урок № 46-169Самоиндукция. Индуктивность. Энергия магнитного поля тока. . . Самоиндукция. - явление возникновения ЭДС индукции в проводящем контуре ...Исследование свойств магнитного поля
Урок-практикум: «Исследование свойств магнитного поля». . (урок совершенствования знаний, формирование умений и навыков). Цели:. Обобщить знания ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 ноября 2018
Категория:Физика
Содержит:61 слайд(ов)
Поделись с друзьями:
Скачать презентацию