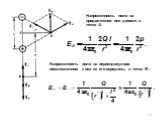
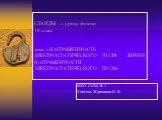
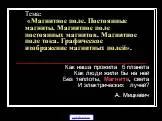
Презентация "Напряжение электростатического поля" по физике – проект, доклад
Презентацию на тему "Напряжение электростатического поля" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 29 слайд(ов).
Слайды презентации
Список похожих презентаций
Конденсатор-энергия электростатического поля
Чему равен суммарный заряд незаряженного проводника? Как размещается избыточный заряд на изолированном проводнике в отсутствие внешнего электростатического ...Электроемкость. Конденсаторы. Энергия электростатического поля
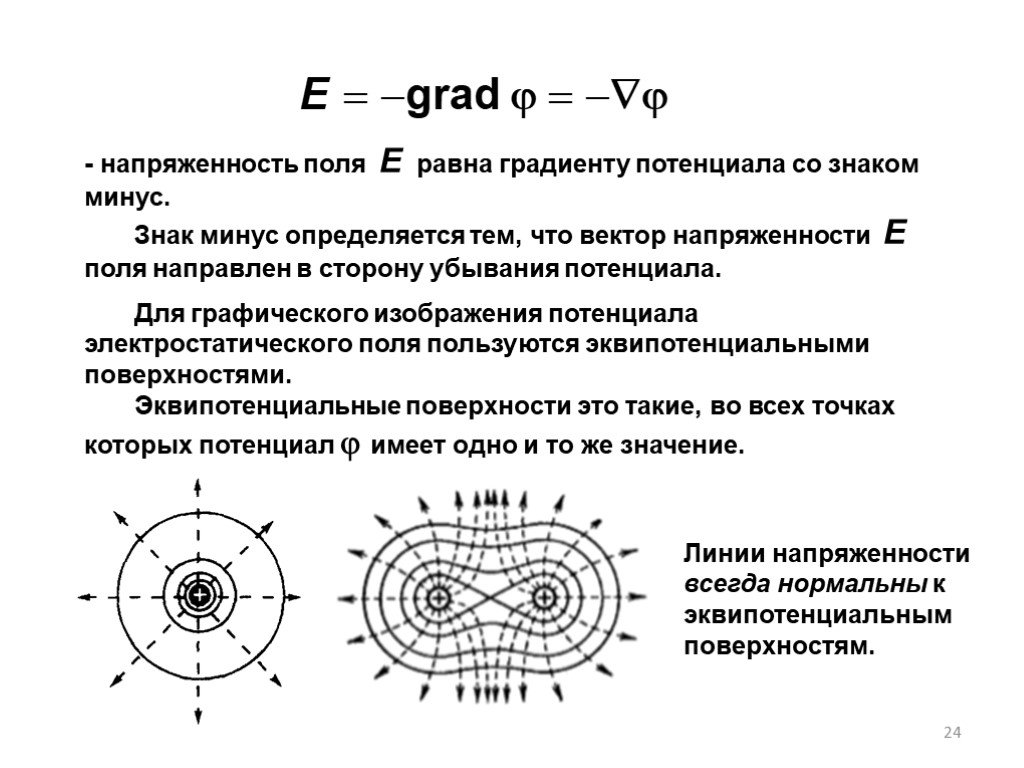
Рассмотрим уединенный проводник, т. е. проводник, который удален от других проводников, тел и зарядов. Его потенциал, согласно ( ), прямо пропорционален ...Потенциал, работа сил электростатического поля
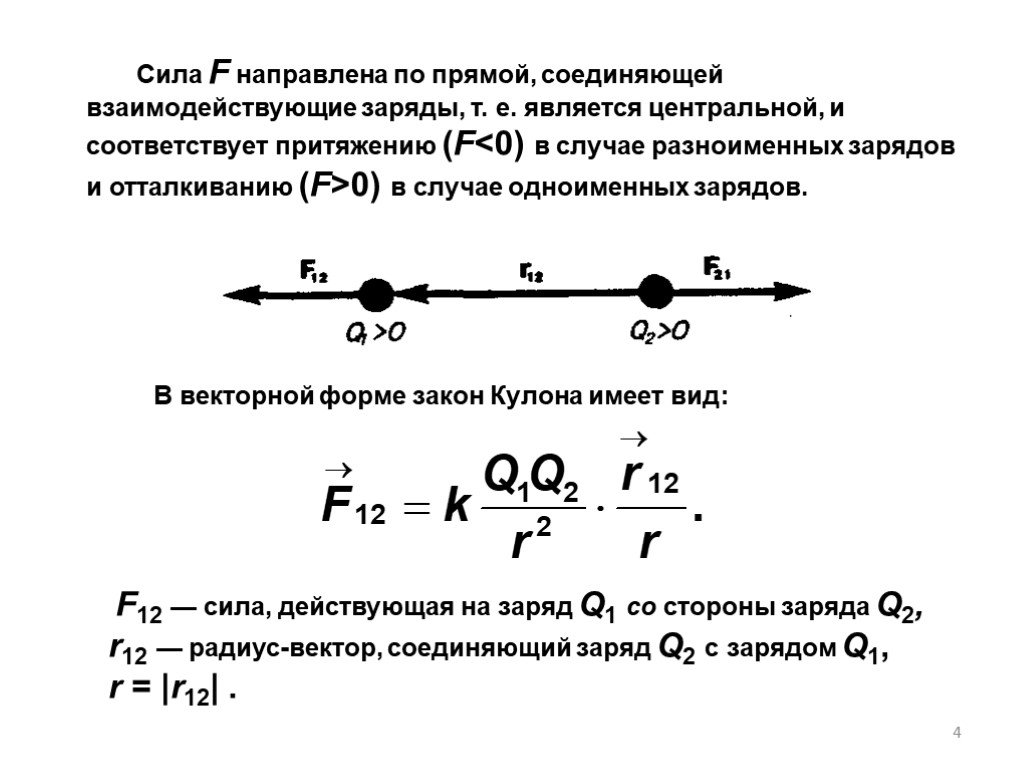
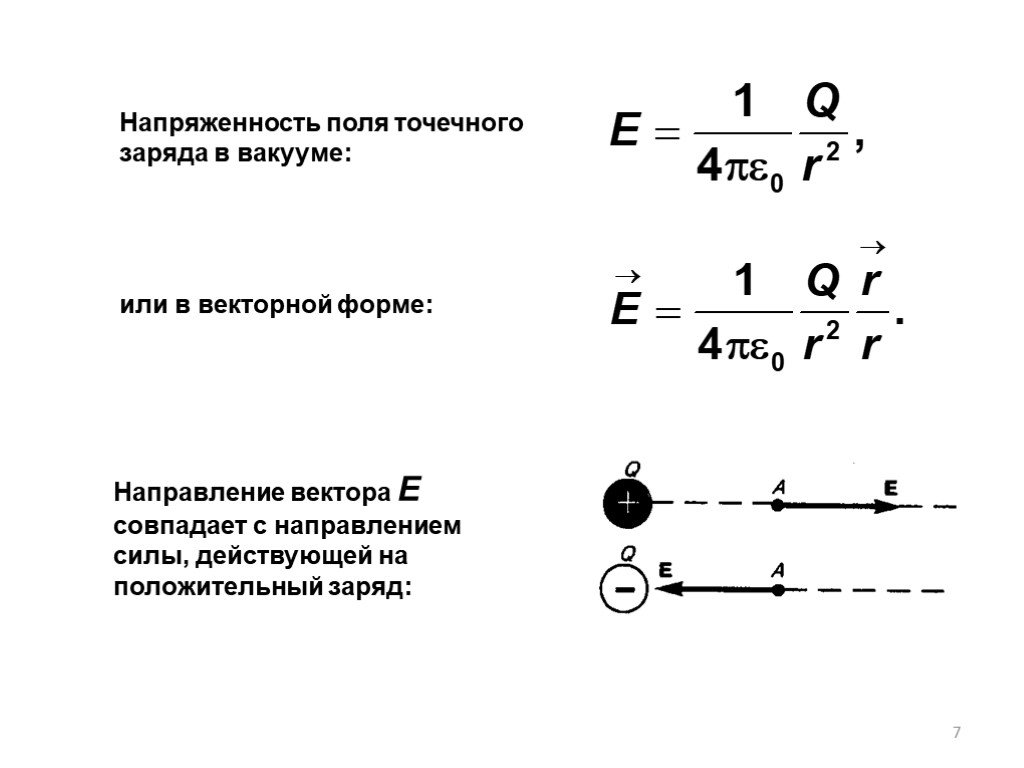
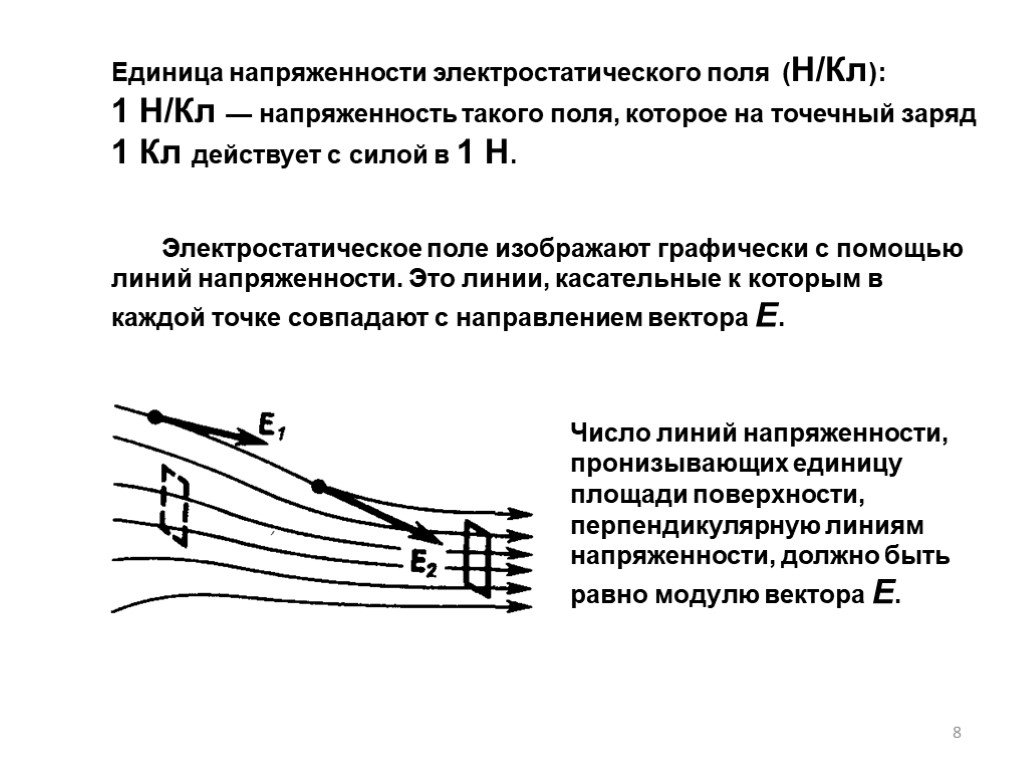
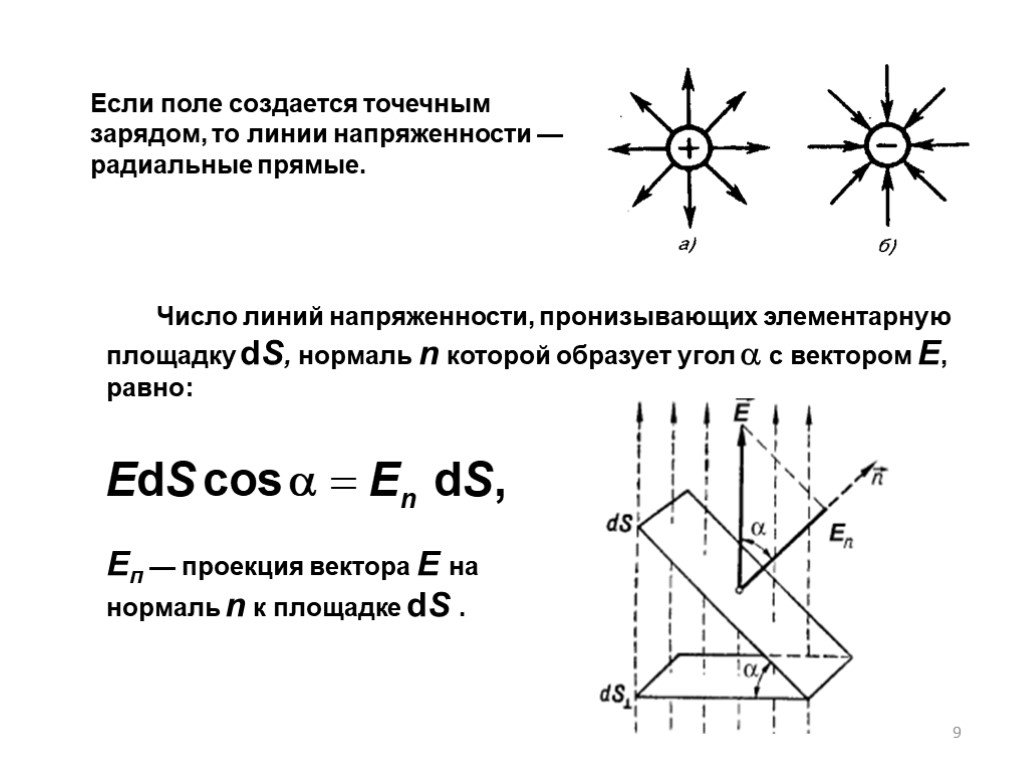
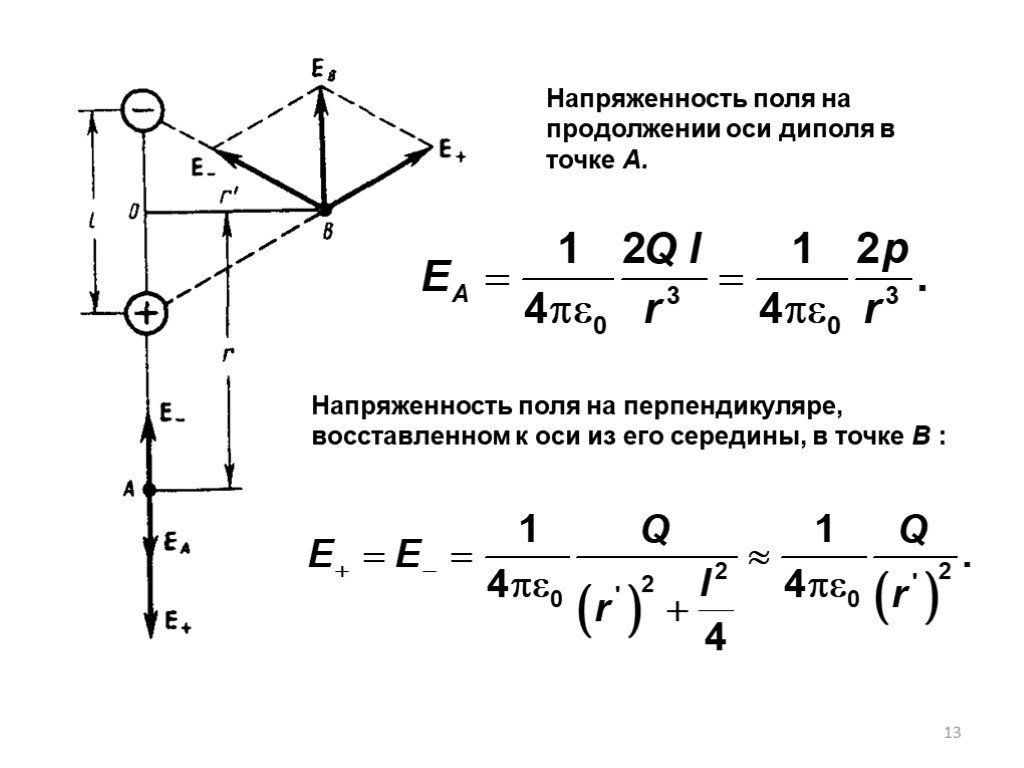
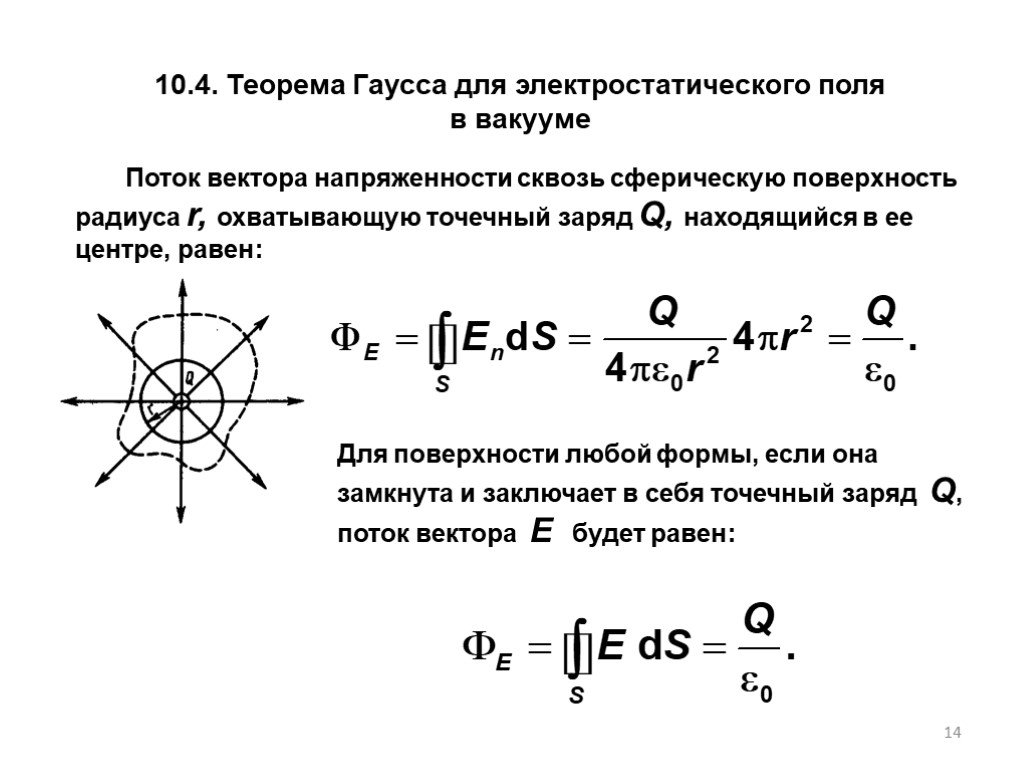
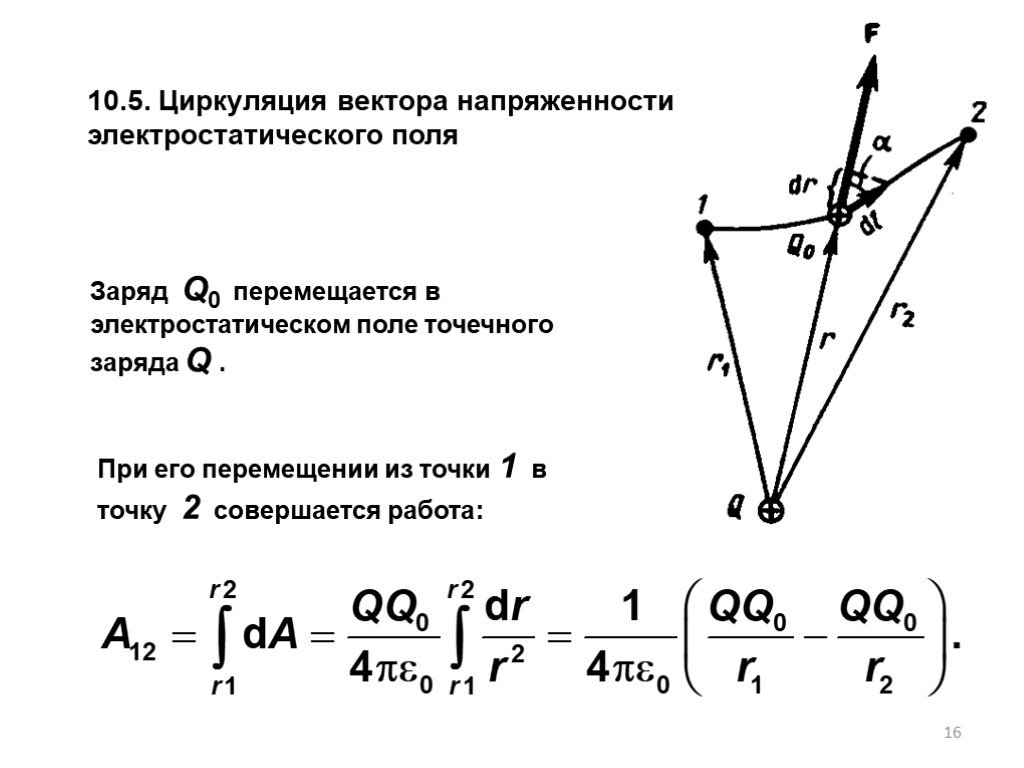
Тема 3. ПОТЕНЦИАЛ И РАБОТА ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ. СВЯЗЬ НАПРЯЖЕННОСТИ С ПОТЕНЦИАЛОМ. 3.1. Теорема о циркуляции вектора 3.2. Работа сил электростатического ...Напряженность электростатического поля
Самостоятельная работа ( 3мин ). Вариант 1. Два точечных заряда величиной -3мКл и 4мКл притягиваются с силой 750 Н. На каком расстоянии находятся ...Характеристика электростатического поля
Wp – потенциальная энергия заряда в электростати-ческом поле. Работа электростатического поля по перемещению заряда. +q d1 1 -q q. , действующая на ...Теория электромагнитного поля
Содержание. Пояснительная записка. Цели и задачи раздела. Психолого - педагогическое объяснение специфики восприятия и освоения учебного материала ...Определение магнитного поля
Тип урока: Комбинированный. Данная тема входит в раздел «Электромагнитные явления», достаточна важная, находит применение при решении практических, ...Напряженность электрического поля
ЭЛЕКТРИЧЕСКОЕ НАПРЯЖЕНИЕ. Напряжение характеризует электрическое поле, создаваемое током. Напряжение ( U ) равно отношению работы электрического поля ...Вариации магнитного поля Земли как составной элемент баз данныхкосмических экспериментов по физике магнитосферы
ЦЕЛЬ. Рассмотреть требования к базам наземных геофизических данных как элементов программ современных космических проектов по опыту нашей предыдущей ...Электрическое поле. Напряжённость электрического поля
Теория близкодействия утверждает, что любое взаимодействие осуществляется с помощью промежуточных агентов и распространяется с конечной скоростью. ...Действие магнитного поля на проводник с током и движущиеся заряды
Магнитное поле оказывает действие на проводник с током, т. е. поле действует на упорядоченно движущиеся электрические заряды. Свободно висящий проводник ...Действие магнитного поля на проводник с током
Магнитное поле действует с некоторой силой на любой проводник с током, находящийся в нем. Если проводник, по которому протекает электрический ток ...Действие магнитного поля на движущуюся заряженную частицу
Определение направления силы Лоренца. Принципиальная схема циклотрона. Частица влетает под углом к магнитному полю. Движение частицы в неоднородном ...Влияние электромагнитного поля на организм человека
За последнее время возник и быстро сформировался новый фак-тор окружающей среды - электромагнитное поле (ЭМП) антропогенного (искусственного) происхождения. ...Влияние электромагнитного поля
Цели и задачи проекта. Цели Понять, как магнитное поле действует на биологические объекты Земли. Научиться работать с информацией. Задачи: Исследовать ...Влияние электрического поля на рост кристаллов
Цель исследования. экспериментальное изучение влияния бесконтактного слабого электрического поля на процесс роста монокристаллов растворимых веществ. ...Физика в познании вещества, поля, пространства и времени
Физика — это наука о наиболее общих и фундаментальных закономерностях, определяющих структуру и эволюцию материального мира. ФИЗИКА. ХИМИЯ – наука ...Влияние магнитного поля на прорастание семян
Мы предполагаем: искусственное магнитное поле положительно влияет на прорастание семян Цель: выявить влияние магнитного поля на прорастание семян. ...Действие магнитного поля на проводники с током
Сила Ампера. Ампер Андре Мари. Ампер - один из основоположников электродинамики, ввел в физику понятие «электрический ток» и построил первую теорию ...Энергетические характеристики электрического поля
Заряд в электрическом поле. На заряд , помещенный в электростатическое поле, действует сила со стороны этого поля. При перемещении заряда эта сила ...Конспекты
Электрическая емкость. Конденсатор. Энергия электрического поля конденсатора
№__________сабақтың жоспары. План урока №___________________. Сабақтың тақырыбы:. . Тема урока. :. Электрическая емкость. Конденсатор. Энергия ...Электромагнитная индукция, самоиндукция, индуктивность. Энергия магнитного поля
Урок по теме «Электромагнитная индукция, самоиндукция, индуктивность. . . Энергия магнитного поля». 11 класс. Цель урока:. . Обобщить знания, ...Самоиндукция. Индуктивность. Энергия магнитного поля тока
Урок № 46-169Самоиндукция. Индуктивность. Энергия магнитного поля тока. . . Самоиндукция. - явление возникновения ЭДС индукции в проводящем контуре ...Сравнение закономерностей гравитационного и электростатического полей
Конспект урока по физике. по теме. «Сравнение закономерностей. гравитационного и электростатического полей». Учитель физики МОУ СОШ ...Направление тока и направление линий его магнитного поля
Тутаев Владимир Александрович. Учитель физики и информатики МБОУ «Ромашкинская СОШ». . с. Ромашкино Курманаевского района Оренбургской области. ...Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки
Урок по теме: «Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки». Цели урока:. . I. Образовательные:. . ...Магнитное поле, его свойства. Магнитное поле постоянного электрического тока. Действие магнитного поля на проводник с током. Сила Ампера. Принцип действия электродвигателя
Урок № 42 – 169 Магнитное поле, его свойства. Магнитное поле постоянного электрического тока. Действие магнитного поля на проводник с током. Сила ...Исследование свойств магнитного поля
Урок-практикум: «Исследование свойств магнитного поля». . (урок совершенствования знаний, формирование умений и навыков). Цели:. Обобщить знания ...Индукция магнитного поля
Аннотация. . Автор материала (ФИО). Малюшова Людмила Григорьевна. . Должность (с указанием преподаваемого предмета). . . Учитель ...Действие магнитного поля на движущийся заряд. Сила Лоренца
Урок № 43-169 Действие магнитного поля на движущийся заряд. Сила Лоренца. Сила Лоренца - сила, действующая со стороны магнитного поля на движущуюся ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:20 февраля 2019
Категория:Физика
Содержит:29 слайд(ов)
Поделись с друзьями:
Скачать презентацию