Конспект урока «Сложные проценты» по математике

Верижникова Татьяна Васильевна

МОУ «СОШ с углубленным изучением отдельных предметов №38» г. Саранск

Учитель математики

Разработка урока: «Сложные проценты».

Цели урока:

Обучающие: обобщить и систематизировать знания по теме «Проценты». Познакомить с формулой «сложных процентов». Совершенствовать умение решать текстовые задачи практической направленности.

Развивающие: развитие умений и навыков сравнения; выявление закономерностей и обобщение учебного материала; творческих способностей в поиске различных способов и методов решения практических задач;

Воспитательные: воспитание мотивов учения, положительного отношения к получению знаний.

Методы: Метод монологического изложения.

Тип урока: комбинированный

Оборудование: ЦОР «Устный счет», таблица «Проценты числа», презентация к теме «Сложные проценты», калькулятор.

Ход урока:

1. Организационный момент

2. Сообщение темы урока

Разгадав математическую шараду, вы узнаете, чем мы будем заниматься на уроке.

Часть слова первая – предлог,

Вторая – мелкая монета,

А весь он, он бы нам помог

При счёте, ну и что же это?

Да, это процент..

Проценты - одно из математических понятий, которое часто встречается в повседневной жизни. Ребята, а в повседневной жизни вы встречались с понятием «процент»? Приведите утверждения с процентами (дети приводят примеры).

Сфера практического приложения процентных расчетов широка. Везде - в газетах, по радио и телевидению, в транспорте и на работе обсуждаются повышение цен, зарплат, рост стоимости акций, снижение покупательной способности населения и т.п. Добавим сюда объявления коммерческих банков, привлекающих деньги населения на различных условиях, сведения о доходах по акциям различных предприятий и фондов, об изменении процента банковского кредита и пр. Все это требует умения производить хотя бы несложные процентные расчеты для сравнения и выбора более выгодных условий. Особый интерес представляет процент в банковских операциях.

3. Актуализация прежних знаний.

Задачи для устной работы.

1. Цены на товары подняли на 50%. Во сколько раз подняли цены?

2. Цены на товары подняли на 100%. Во сколько раз подняли цены?

3. Цены на товары подняли на 200%. Во сколько раз подняли цены?

4. Зарплату увеличили в 2 раза, а цены на все товары снизили на 50%. Что стало с покупательной способностью?

5. Зарплата уменьшилась на 50%, все цены повысились на 200%. Оценить динамику моей покупательной способности.

6. Зарплата не изменилась, все цены снизили на 100%. Что теперь стало с покупательной способностью?

4. Изучение нового материала.

Назовите основные задачи, связанные с процентами?

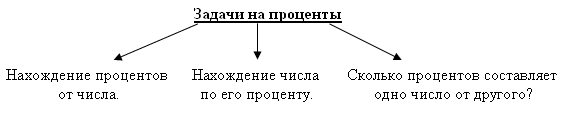
Сегодня на уроке мы научимся решать задачи с помощью формул «простых и сложных» процентов. Эти термины чаще всего встречаются в банковских делах, в финансовых задачах. Банки привлекают средства (вклады) за определенные процентные ставки. В зависимости от процентной ставки вычисляется доход.

На практике применяются два подхода к оценке процентного дохода – простые и сложные проценты.

При применении простых процентов доход рассчитывается от первоначальной суммы вложенных средств не зависимо от срока вложения. В финансовых операциях простые проценты используются преимущественно при краткосрочных финансовых сделках.

Пусть некоторая величина подвержена поэтапному изменению. При этом каждый раз ее изменение составляет определенное число процентов от значения, которое эта величина имела на начальном этапе. Так вычисляются простые проценты.

При применении сложных процентов накопленная сумма процентов добавляется во вклад по окончании очередного периода начислений. При этом каждый раз ее изменение составляет определенное число процентов от значения, которое эта величина имела на предыдущем этапе. В этом случае имеем дело со “сложными процентами” (т.е. используются начисления “процентов на проценты”)

Первоначальная сумма и полученные проценты в совокупности называются накопленной (наращенной) суммой.

Пусть денежный вклад, равный А рублей, через год возрастает на P%.

Тогда к концу года он станет равным А₁=А+А*=А*(1+)руб.,

еще через год А₂= А*(1+)+ А*(1+)*=А*(1+)²руб.,

а через n лет : А_n = А*(1+)ⁿ - эту формулу называют формулой сложных процентов.

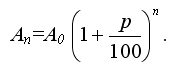
5. Формирование умений и навыков.

Задача 1. Какая сумма будет на счете через 5 лет, если на него внесено 5000 рублей под 20 % годовых?

Решение. Задача на сложный процентный рост:

.

Что означают параметры в формуле и чему они равны?

p - начальный капитал – 5000 рублей;

i - процентная ставка – 0,2;

k – конечный капитал;

n – число лет –5 лет.

Банковские операции

Задача2. За хранение денег сбербанк начисляет вкладчику 9 % годовых. Вкладчик положил на счёт 10000 р. и решил в течение пяти лет не снимать деньги со счёта и не брать процентные начисления. Сколько денег будет на счете вкладчика через год? через два года? через пять лет?

Решение.

Задача на сложный процентный рост:

p - начальный капитал – 10000 рублей;

i - процентная ставка – 0,09;

k – конечный капитал;

n – число лет – 1 год; 2 года. 5 лет.

Для n = 5 конечный капитал вычислить самостоятельно.

.

6. Подведение итогов урока. Рефлексия. Д/з.

С какими новыми понятиями мы познакомились на уроке?

Что такое «сложный процент»?

Как его найти?

Где используются «простые и сложные» проценты?

Какие трудности вы испытывали при решении задач?

Чему научились?

Оцените свою работу на уроке.

Источники информации.

1. По материалам сайта: Инструменты финансового анализа.

2. По материалам: Крамор В.С., Лунгу К.М. Повторяем и систематизируем школьный курс алгебры: пособие для старшеклассников и абитуриентов. Ч.1. – М.: АРКТИ, 2001.