Конспект урока «Задачи на движение» по математике для 11 класса
Урок по математике. 11класс.
Тема: Задачи на движение (подготовка к ЕГЭ по математике 2ч)
Учителя математики – Познахарёвой И.Ю. МКОУ СОШ №1 г-к Кисловодска Ставропольского края.
Тип урока: совершенствование умений и навыков
Цели урока:
- дидактическая: обобщение и систематизация методов решения задач на движение, включенных в открытый банк задач по математике;
- развивающая: развитие творческих способностей применения знаний и умений при решении вариантов ЕГЭ;
- воспитательная: создать условия для развития умений проводить аргументированные рассуждения, делать логически обоснованные выводы, ясно, точно и грамотно выражать свои мысли в устной и письменной речи.
Средства наглядности: карточки для самостоятельной работы, карточки для работы в группах, электронные образовательные ресурсы.
| Время (мин) | Деятельность | ||
| учителя | учащегося | ||
Сегодня на уроке мы обобщим и систематизируем знания и умения при решении задач на движение, применяя не только изученные методы, но и нестандартные подходы. Итак, начинаём путешествие по теме «Задачи на движение из открытого банка заданий».
Чтобы перейти к решению задач разделим их по способам решения: - арифметический способ; - задачи на составление уравнений и систем уравнений; - задачи на прямую и обратную зависимость; - задачи на проценты; - задачи решаемые нестандартными способами Для решения задачи выбираем наиболее рациональный способ. Задача 1. Теплоход скорость которого в неподвижной воде равна 20 км/ч, проходит по течению реки до пункта назначения и после стоянки возвращается в исходный пункт. Найдите расстояние, пройденное теплоходом за весь рейс, если скорость течения равна 4 км/ч, стоянка длится 3 часа, а в исходный пункт теплоход возвращается через 13 часов после отплытия из него. Ответ дайте в километрах. (решение см Приложение3) Задача 2. Города А, В и С соединены прямолинейным шоссе, причем город В расположен между городами А и С. Из города А в сторону города С выехал легковой автомобиль, и одновременно с ним из города В в сторону города С выехал грузовик. Через сколько часов после выезда легковой автомобиль догонит грузовик, если скорость легкового автомобиля на 28 км/ч больше скорости грузовика, а расстояние между городами А и В равно 112 км? Задача 3. Пешеход и велосипедист отправились одновременно навстречу друг другу из разных городов, расстояние между которыми 40 км. Велосипедист проехал мимо пешехода через 2 ч после отправления и на весь путь затратил на 7,5 ч меньше, чем пешеход. Найти скорость движения каждого, считая, что они двигались все время с постоянными скоростями. (Решение задачи см приложение)
(Приложение 4)
На уроке вспомнили теорию и традиционные способы решения задач на движение предлагаю самостоятельную работу на 3 варианта по 2 задачи в каждом. На выполнение работы отводится 15 мин. Проверку работы проведем в виде самоконтроля по таблице с ответами всех вариантов.
Проверьте правильность составления уравнения и ответ — 3 мин. Далее на уроке рассмотрим задачи на движение повышенной сложности, решаемые нестандартными методами - задачи на прямую и обратную зависимость, задачи на проценты, нестандартные задачи.
№ 1. Поезд прошел мимо неподвижного стоящего на платформе человека за 6 с, а мимо платформы длиной 150 м за 15 с. Найти скорость движения поезда и его длину. № 2. Из пункта А в пункт В вышел пешеход и одновременно из В в А выехал велосипедист. Пешеход прибыл в В через 3 часа после встречи, а велосипедист в А через 45 мин после встречи. Сколько часов был в пути пешеход?
Каждая группа получает задание – карточку с 2 задачами. На выполнение заданий отводится 15 минут. Каждая группа может взять консультацию учителя. Цель работы в группах проверить уровень ваших знаний и умений. Оценивание работы: быстрое правильное решение, четкое объяснение задач. 1 группа №1.Велосипедист и пешеход отправились одновременно из пункта А в пункт В. Скорость велосипедиста была в 2 раза больше скорости пешехода, но в пути он сделал остановку для устранения поломки велосипеда и поэтому в пункт В прибыл лишь на 5 минут раньше пешехода, который на весь путь затратил 40 мин. Сколько минут велосипедист устранял поломку велосипеда? № 2 Моторная лодка проходит расстояние между пристанями А и В по течению реки за 20 мин, а против течения за 1 час. Во сколько раз собственная скорость моторной лодки больше скорости течения реки? 2 группа № 1. Некоторое расстояние планировали проехать с постоянной скоростью, а проехали расстояние на 40% большее и со скоростью на 75% большей. На сколько процентов время движения оказалось меньше запланированного? № 2. Из А в В и из В в А выехали одновременно два мотоциклиста. Первый прибыл в В через 2,5 ч после встречи, а второй прибыл в А через 1,6 ч после встречи. Сколько часов был в пути каждый мотоциклист? 3 группа № 1. Велосипедист и пешеход отправились одновременно навстречу друг другу из городов А и В. После встречи велосипедист прибыл в город В через1 час, а пешеход пришел в город А через 4ч. Во сколько раз скорость велосипедиста больше скорости пешехода? № 2. Из города по двум взаимно перпендикулярным дорогам вышли в разное время два пешехода, Скорость первого пешехода 4 км/ч, а второго 5 км/ч. Сейчас первый находится в 7 км от города, а второй - в 10 км. Через сколько часов расстояние между пешеходами будет равно 25 км?
Решение (Приложение 9) 11. Домашнее задание 12. Итоги урока Сегодня на уроке мы систематизировали и обобщили типы и методы решения задач на движение, составляли математические модели практических задач, решали уравнения, применяли знания и умения при решении задач, включенных в открытый банк задач по математике для подготовки к ЕГЭ.
| 1 мин 2 мин 3 мин 15 мин 4 мин 17 мин 2 мин 1 мин 10 мин 15 мин 16 мин 1 мин 2 мин | Организационная Сообщает тему урока, дату проведения урока, цели урока Проводит фронтальный опрос по теории задач на движение (Приложение 1 - презентация) Констатирует факты: vпо теч. v собст; v собст > vпротив теч; vтеч.реки vсобст; v= 0, то тело неподвижно; t = t1 + t2, если по условию известно затраченное время туда и обратно. Вызывает к доске учащихся для решения задач. Проводит анализ задачи. Демонстрирует условие задачи через мультимедиа проектор. Следит за правильными рассуждениями. Выбирает вместе с учащимися метод решения, проверяет решение индивидуального задания Обсуждает способ решения задачи, следит за правильным оформлением решения, заслушивает решение индивидуального задания. Проводит теоретический бой по вопросам между вариантами. Настраивает учащихся на выполнение самостоятельной работы. Объясняет цель работы, время работы, сообщает количество заданий и вариантов, как будет проверяться работа. Раздает задания с карточками (Приложение 5) Демонстрирует таблицу ответов, предлагает проверить составление уравнения и ответ. Проводит опрос: определение прямой и обратной пропорциональной зависимости, свойства прямой и обратной пропорциональной зависимости, определение процента, теорему Пифагора. Объясняет решение задачи, демонстрирует слайд (Приложение 7). Совместно с учащимися выбирает метод решения, ведет рассуждения. Предлагает работу в группах. Делит класс на 4 группы. Объясняет ход работы. Раздает карточки (Приложение 8). Дает консультации, следит за ходом работы в группах. Вызывает одновременно 3 учащихся для защиты задач, оценивает решение Подобрать по 2 нестандартные задачи на движение, из любых источников, включая Интернет ресурсы Если время останется, то учитель задает вопросы по теме. | Сообщают о готовности к уроку Записывают в тетради Учащиеся в устной форме отвечают на вопросы по презентации Учащиеся активно отвечают. Один ученик решает доске, остальные в тетрадях. Один ученик работает индивидуально на закрытой доске (Приложение 3) Учащиеся строят таблицу по условию задачи. Один ученик заполняет на доске таблицу и далее задачу № 2 решает устно. Один ученик выполняет индиви- дуальное задание по карточке в тетради. (Приложение 3) Ученик решает задачу на доске полностью с подробным обоснованием, остальные записывают решение в тетрадь Учащиеся отвечают на вопросы другого варианта. Учащиеся внимательно слушают, приступают к выполнению заданий. Учащиеся проверяют по таблице запись уравнения и ответ. Самооценка в виде отметки. Учащиеся отвечают Учащиеся записывают в тетрадь. Предлагают методы решения, ведут записи. Учащиеся слушают. Приступают к выполнению. Учащиеся обсуждают решения задач, ведут записи, назначают учеников для защиты. 3 учащихся проводят защиту работ, остальные записывают решения и пояснения в тетрадь, участвуют в защите задач, дают оценку группам по защите. Учащиеся записывают домашнее задание. Учащиеся отвечают. |
| | | | |
| | | | |
Приложение 1.




Приложение 2.
Решение задач
№ 1.
Решение.
| Скорость | Время | Расстояние | |
| Неподвижная вода | 20 км/ч | | |
| По течению | 20 + 4 = 24 км/ч |
| Х км |
| Против течения | 20 – 4 = 16 км/ч |
| Х км |
| Течение реки | 4 км/ч | | |
| Стоянка | | 3 ч | |
Как составим уравнение? ![]() +
+ ![]() = 10, 5х = 480, х = 96, Расстояние, пройденное теплоходом равно 96 х 2 = 192 км. Ответ: 192 км.
= 10, 5х = 480, х = 96, Расстояние, пройденное теплоходом равно 96 х 2 = 192 км. Ответ: 192 км.
№ 2. Анализ. Назовите вид движения. Равны ли скорости легкового и грузового автомобиля? Неизвестны ни время движения, ни расстояние, есть только взаимосвязь между скоростями, поэтому введем две неизвестные величины (демонстрируется слайд с таблицей).
Р ешение. 112 км
ешение. 112 км
 А В С
А В С

| Скорость | Время | Расстояние | |
| Из А в С легковой авт | Х + 28 км/ч | У ч | Х |
| Из В в С - грузовик | Х км/ч | У ч | ХУ км |
ХУ + 28 У – ХУ = 112, 28 у = 112, у = 4 Ответ: 4 часа.
№ 3. Анализ. Назовите вид движения. Используя вопрос задачи введите переменные, учитывая, что нет взаимосвязи между скоростями.
| Скорость | Время | Расстояние | |
| Велосипедист | Х км/ч | 2 ч | 2 |
| Пешеход | У км/ч, у | 2 ч | 2У км |
| | | | |
| В | Х км\ч | 40/х ч | на 7,5 ч меньше |
| Пешеход | У км\ч | 40/у ч | |
Составим систему уравнений
 2х + 2у = 40 х + у = 20
2х + 2у = 40 х + у = 20
40/у — 40/х = 7,5 40/у — 40/х = 7,5. Один учащийся решает эту систему на доске.
Приложение 3.
Индивидуальные карточки с задачами
№ 1. Проехав за 1 час три четверти расстояния между городами А и В , водитель увеличил скорость на 20км/час, поэтому остаток пути он проехал за 15 мин. Определите расстояние между городами А и В.
Решение:
Пусть х км – это ¾ расстояния
Тогда 4/3х км – это путь между городами А и В
| Скорость | Время | Расстояние | |
| 1 участок – с заданной скоростью | Х км/ч | 1 ч | Х км |
| 2 участок – после увеличения скорости | Х + 20 км/ч | 15 мин = ¼ ч | ¼х + 5 км |
Составим уравнение:
Х + ¼х + 5 = 4/3х
1/3х = 60
х = 180
180 км расстояние до повышения скорости
4/3 · 180 = 240 км
Ответ: 240 км
№ 2. Пешеход вышел из города А в город В . Через час после этого навстречу ему выехал велосипедист из города В в город А.Через 2ч после своего выезда велосипедист встретился с пешеходом, а через 1 ч после встречи прибыл в город А. Сколько времени был в пути пешеход?
Решение:
Т.к. время велосипедиста после встречи меньше времени пешехода в 3 раза, то пешеход после встречи затратил времени в 3 раза больше, чем было затрачено велосипедистом т.е. обратно пропорциональная зависимость величин 2 · 3 = 6 ч или ![]() , тогда пешеход был в пути 6 + 3 = 9 ч.
, тогда пешеход был в пути 6 + 3 = 9 ч.
Ответ: 9 ч
Приложение 4.


Приложение 5.
Карточки для самостоятельной работы
1 вариант
1. Лодка в 5:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 2 часа, лодка отправилась назад и вернулась в пункт А в 23:00. Определите (в км/час) скорость течения реки, если известно, что собственная скорость лодки равна 4 км/ч.
2. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 77 км. На следующий день он отправился обратно со скоростью на 4 км/ч больше прежней. По дороге он сделал остановку на 4 ч. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
2 вариант
1. Моторная лодка прошла против течения реки 195 км и вернулась в пункт отправления, затратив на обратный путь на 2 часов меньше, чем на путь против течения. Найдите скорость течения, если скорость лодки в неподвижной воде равна 14 км/ч. Ответ дайте в км/ч.
2. Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 27 км/ч, а вторую половину пути проехал со скоростью, на 18 км/ч большей скорости первого, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста. Ответ дайте в км/ч.
3 вариант
1. От пристани А к пристани В отправился с постоянной скоростью первый теплоход, а через 3 часа после этого следом за ним со скоростью, на 3 км/ч большей, отправился второй. Расстояние между пристанями равно 238 км. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно. Ответ дайте в км/ч.
2. Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути проехал со скоростью 78 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 48 км/ч. Ответ дайте в км/ч.
Приложение 6.
Самоконтроль (слайд)
Проверьте правильность составления уравнения и ответ, поставьте оценку.
| 1 вариант | 2 вариант | 3 вариант | |
| № 1 Уравнение |
|
|
|
| Ответ | 1 км/ч | 1 км/ч | 14 км/ч |
| № 2 Уравнение |
|
|
|
| Ответ | 7 км/ч | 36 км/ч | 52 км/ч |
Приложение 7.
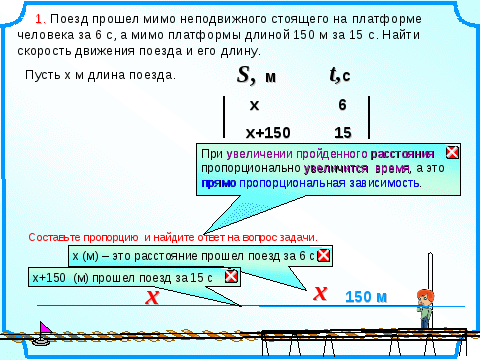

Приложение 8.
1 группа
№1.Велосипедист и пешеход отправились одновременно из пункта А в пункт В. Скорость велосипедиста была в 2 раза больше скорости пешехода, но в пути он сделал остановку для устранения поломки велосипеда и поэтому в пункт В прибыл лишь на 5 минут раньше пешехода, который на весь путь затратил 40 мин. Сколько минут велосипедист устранял поломку велосипеда?
№ 2 Моторная лодка проходит расстояние между пристанями А и В по течению реки за 20 мин, а против течения за 1 час. Во сколько раз собственная скорость моторной лодки больше скорости течения реки?
2 группа
№ 1. Некоторое расстояние планировали проехать с постоянной скоростью, а проехали расстояние на 40% большее и со скоростью на 75% большей. На сколько процентов время движения оказалось меньше запланированного?
№ 2. Из А в В и из В в А выехали одновременно два мотоциклиста. Первый прибыл в В через 2,5 ч после встречи, а второй прибыл в А через 1,6 ч после встречи. Сколько часов был в пути каждый мотоциклист?
3 группа
№ 1. Велосипедист и пешеход отправились одновременно навстречу друг другу из городов А и В. После встречи велосипедист прибыл в город В через1 час, а пешеход пришел в город А через 4ч. Во сколько раз скорость велосипедиста больше скорости пешехода?
№ 2. Из города по двум взаимно перпендикулярным дорогам вышли в разное время два пешехода, Скорость первого пешехода 4 км/ч, а второго 5 км/ч. Сейчас первый находится в 7 км от города, а второй - в 10 км. Через сколько часов расстояние между пешеходами будет равно 25 км?
Приложение 9.
Группа 1
№ 1. Решение:
1.Т.к.скорость велосипедиста в 2 раза больше, то время должно быть в 2 раза меньше, а значит 20 мин.
№ 2 Решение:
Велосипедист потратил 35мин, а значит он устранял поломку 35-20=15мин.
Ответ: 15мин.
Решение:
х - собственная скорость, у - скорость течения реки. Тогда отношение скоростей по течению к скорости против течения будет следующим:
![]()
х + у=3(х -у), 2х = 4у, ![]()
Ответ: в 2 раза
Группа 2.
№ 1. Решение:
| 100 % | |
| Затраченное время t1 | Х % |
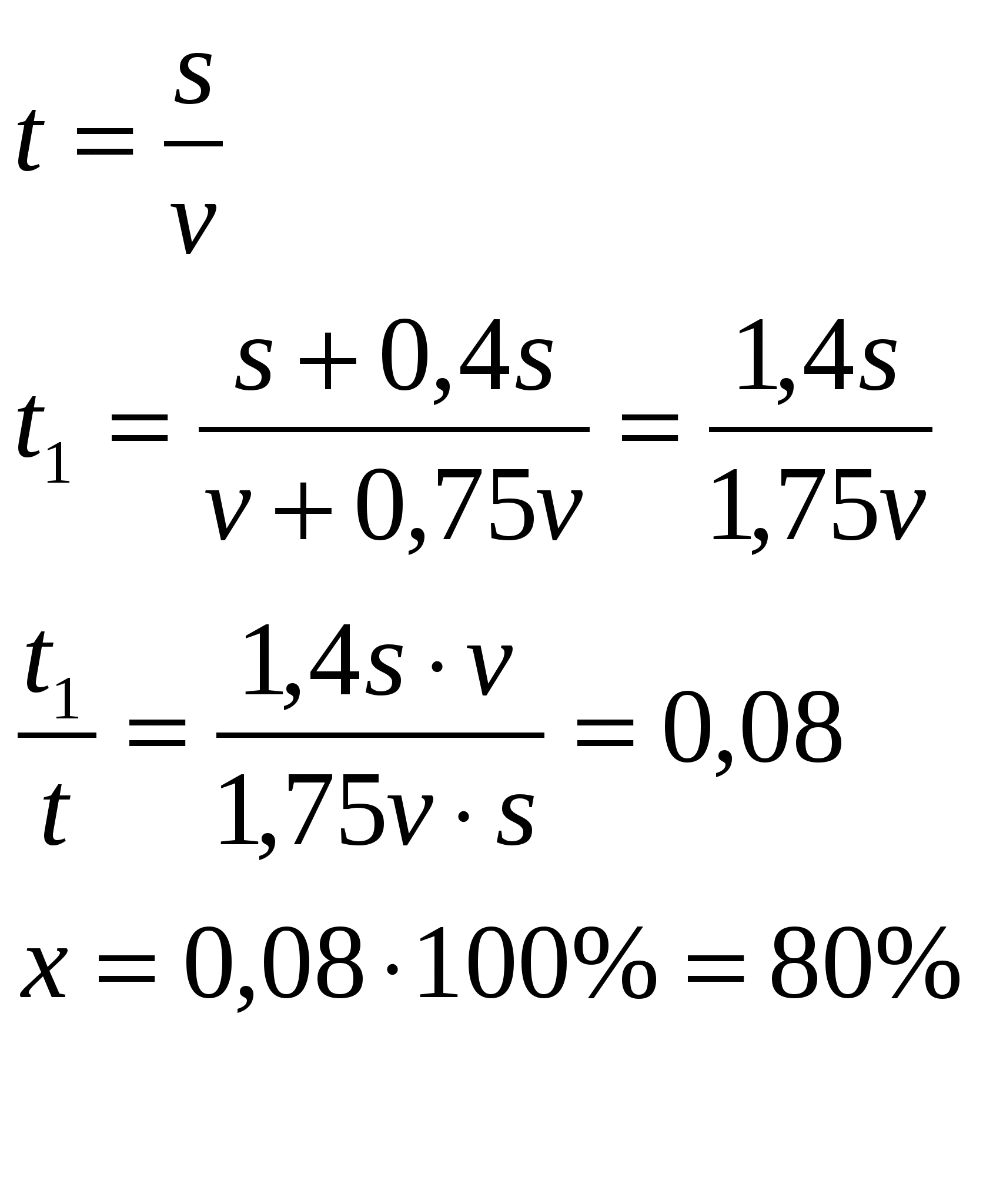
Следовательно 100% - 80% = 20% время движения оказалось меньше запланированного.
Ответ: на 20 %.
№ 2. Решение:
пусть х ч – время до встречи,
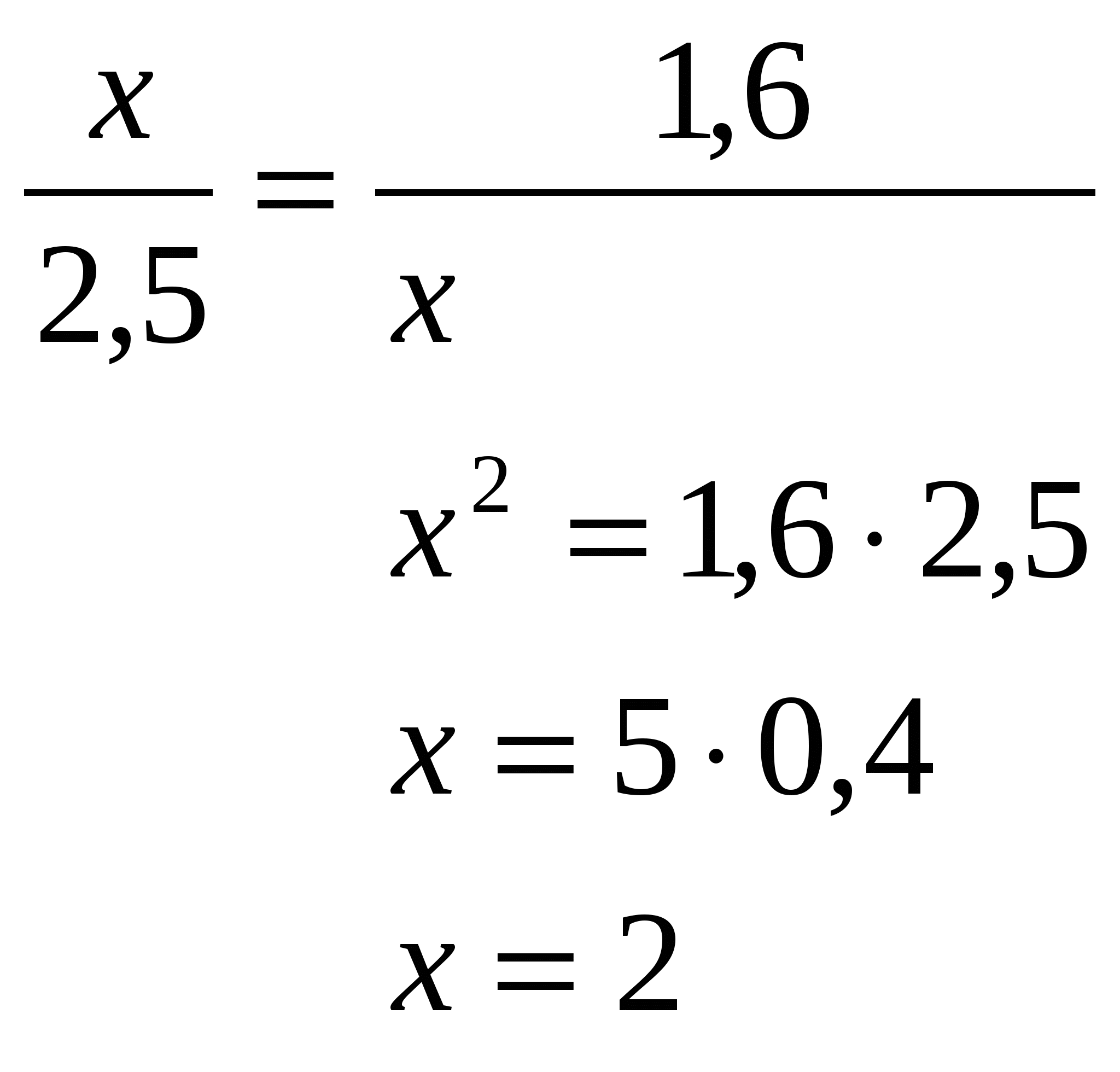
тогда время 1 мотоциклиста 4,5 ч, а другого – 3,6 ч.
Ответ: 4,5 ч или 3,6 ч
Группа 3.
№ 1. Решение:
v - скорость велосипедиста
v1 – скорость пешехода
v · 1 = v км путь велосипедиста после встречи
v1 · 4 = 4 v1 км путь пешехода после встречи
t = 4 v1/ v ч время велосипедиста до встречи
t1 = v/ v1 ч время пешехода до встречи
Т.к. время до встречи одинаково, то 4 v1/ v = v/ v1 , v/ v1= 2.
Ответ: в 2 раза.
№ 2.
4 км/ч - скорость одного пешехода
5 км/ч – скорость другого пешехода
Пусть t ч общее время движения пешеходов, причем t > 0
7 + 4t км – путь одного пешехода
10 + 5t км – путь другого пешехода, по условию известно, что через некоторое время расстояние между ними будет 25 км, а так пешеходы движутся в перпендикулярном направлении относительно друг друга, то по теореме Пифагора составим уравнение:
(7 + 4t)2 + (10 + 5t)2 = 625
49 + 56t + 16t2 + 100 + 100t +25t2 = 625
41t2 + 156t – 476 = 0
D = 25600
t1 = 2; t2
Здесь представлен конспект к уроку на тему «Задачи на движение», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (11 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

 У + 28 У км на 112 км больше
У + 28 У км на 112 км больше Х км 40 км
Х км 40 км  елосипедист
елосипедист 