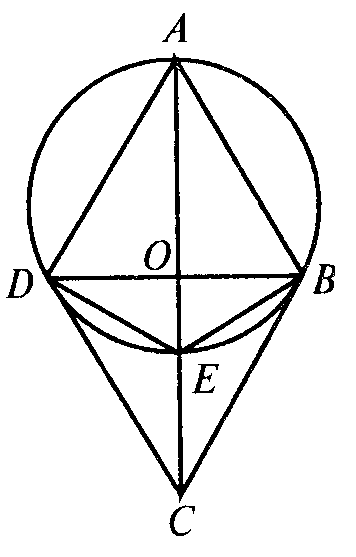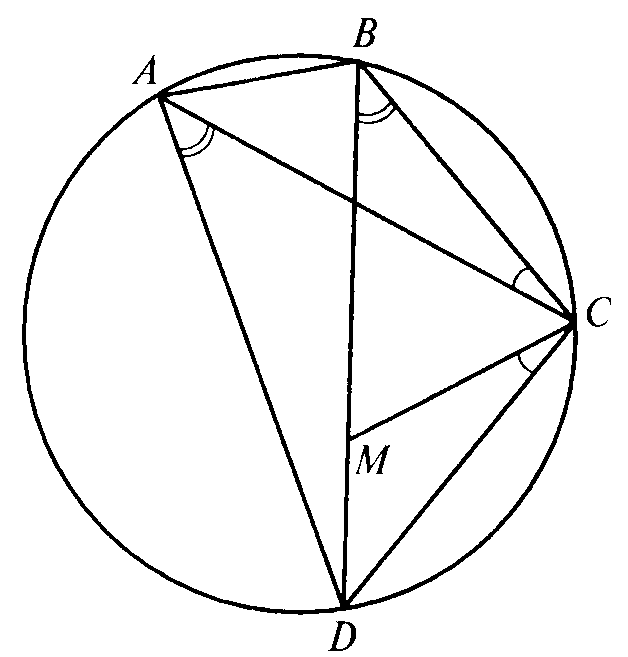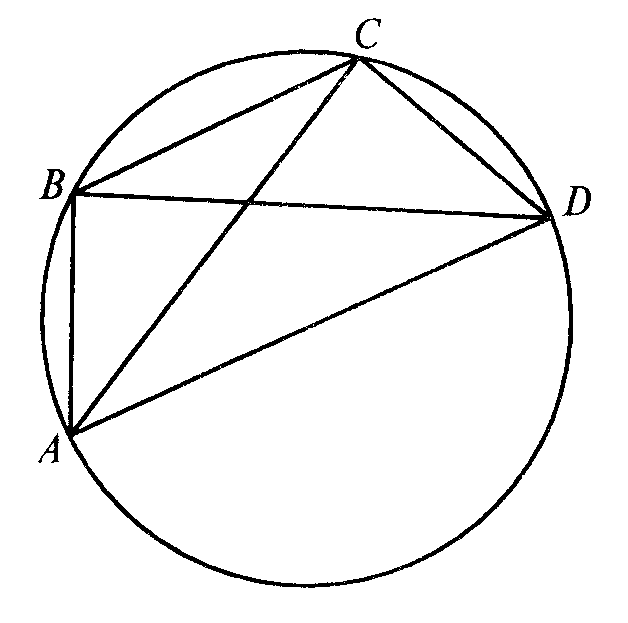Конспект урока «Свойства вписанных четырехугольников» по математике

Название современных образовательных технологий, применяемых в УВП

Этапы урока/занятия, на которых технология применяется

Компетенции

1

Технология критического мышления

1.Организационный этап Самоопределение к деятельности. Включение в деловой ритм. Устное сообщение преподавателя. Подготовка взвода к работе.

2.Рефлексия деятельности

Суворовцы осуществляют самооценку собственной учебной деятельности, соотносят цель и результаты, степень их соответствия

Личностные: самоопределение; смыслообразование;

коммуникативные:

планирование учебного сотрудничества с преподавателем и сверстниками; умение с достаточной полнотой и точностью выражать свои мысли;

познавательные: рефлексия

2

ИКТ + технология индивидуально – групповой деятельности

1. Подготовка к активной познавательной деятельности

Актуализация темы урока через познавательную деятельность обучающихся..

Познавательные: логические – анализ объектов с целью выделения признаков;

коммуникативные: общение в группе, ответы на вопросы;

социальные ( умение использовать знания и другие ресурсы для решения проблемы).

3

4.

Технология проблемного обучения

Технология развивающего обучения

1.Этап оперирования знаниями, умениями и навыками при решении практических задач

Формирование практических умений и навыков по решению задач разной степени сложности.

1.Подготовка к активной учебно- познавательной деятельности

Формирование новых знаний

2.Формирование и закрепление умений и навыков.

Регулятивные: целеполагание;

Коммуникативные: постановка вопросов; познавательные: общеучебные-самостоятельное выделение– формулирование познавательной цели; логические- формулирование проблемы.

Учебно-познавательная:

подготовка доклада и презентации;

информационная:

получение дополнительной информации, ее анализ;

математическая

Содержание урока

Время

Работа суворовцев

1

2

3

4

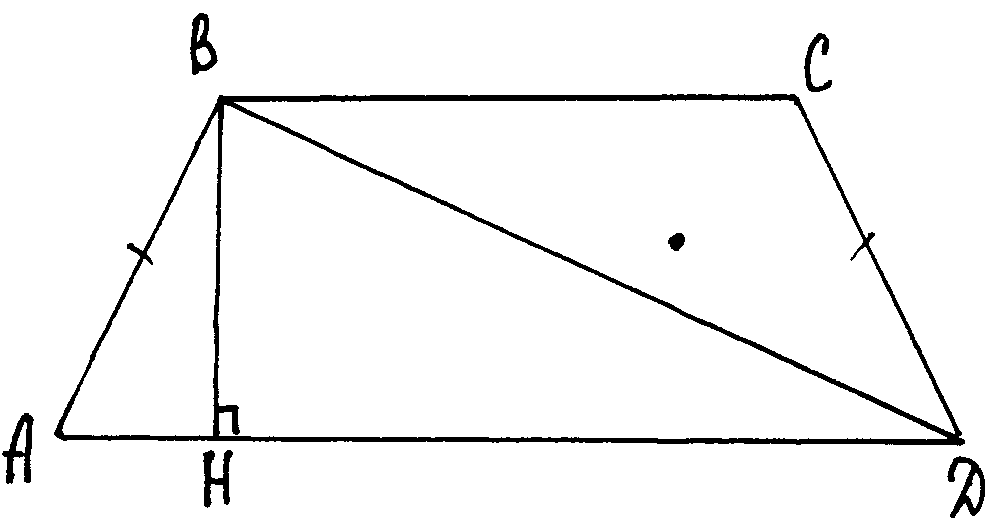
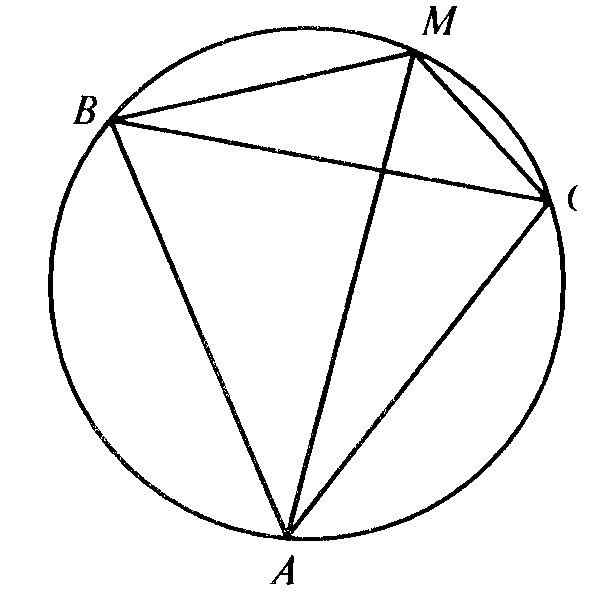
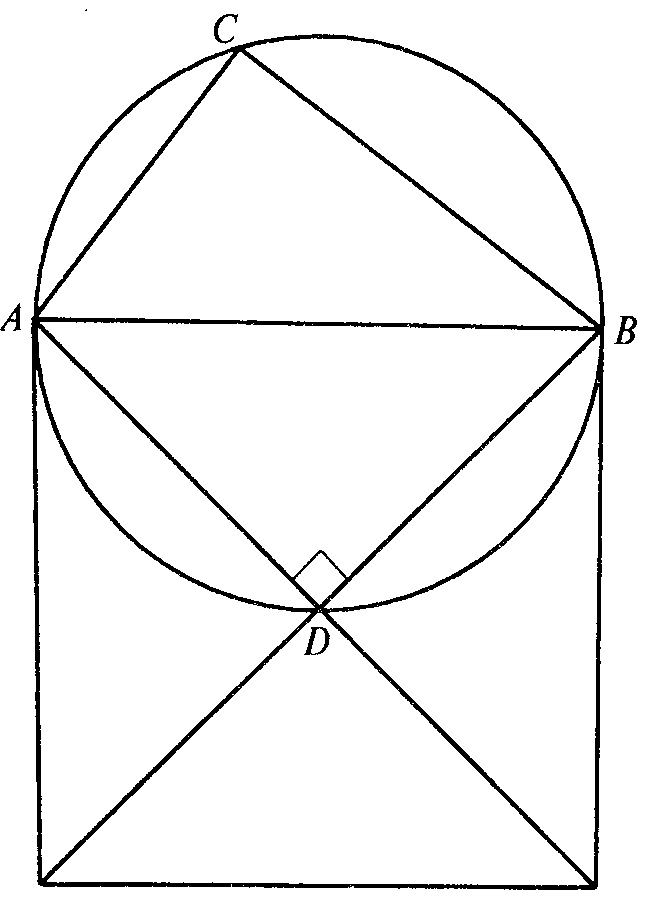
1.

2.

3.

Организационный момент.

Подготовка к активной учебно-познавательной деятельности.

Повторение теоретического материала проводится в виде соревнования двух команд, которые задают друг другу подготовленные на самоподготовке вопросы, включающие определения вписанных многоугольников и описанной окружности, свойства вписанных четырехугольников.

Рассмотрим решения задач из задания на самоподготовку.

Задача1. Боковая сторона равнобедренной трапеции равна ,

а основания равны 3 и 4. Найдите длину диагонали трапеции.

Р е ш е н и е. Проведем ВН – перпендикуляр к АD. Тогда

ВН =13-0,25=12,75, ВD =12,75+12,25=25, откуда BD=5.

Ответ: 5.

Задача 2. Дан ромб, окружность, описанная около треугольника АВД, пересекает большую диагональ ромба АС в точке Е.

Найдите СЕ, если АВ=8, ВД=16.

Р е ш е н и е. Угол EDA – прямой, т.к.он вписанный и опирается на полуокружность. Треугольник EDA –прямоугольный, DOFE, тогда DO=AO ∙ OE. Из треугольника АОВ находим АО=16, следовательно, ОЕ=4 и СЕ=12.

Ответ: 12.

На сегодняшнем уроке мы рассмотрим еще одно свойство вписанных четырехугольников, теорему Птолемея. Сначала -историческая справка.

Формирование и закрепление умений и навыков.

Теорема Птолемея. Произведение диагоналей вписанного четырехугольника равно сумме произведений противоположных сторон четырехугольника.

AB ∙ CD + AD ∙ BC = AC ∙ BD

Д о к а з а т е л ь с т в о. На диагонали ВD возьмем точку М, так что МСD = ВСА. Тогда треугольники АВС и DМС подобны

( МDС= ВАС, как вписанные углы , опирающиеся на одну дугу ВС ). Следовательно, АВ:МD =АС: DС,

АВ ∙ DС=АС ∙ МD. (1)

ВСМ = ВСА + АСМ,

АСD =DСМ + АСМ, значит, ВСМ = АСD .

Следовательно, треугольники ACD и ВСМ подобны

( DСА= DВС, как вписанные углы, опирающиеся на одну дугу DС) и AD : ВМ=АС:ВС, откуда

АD ∙ ВС=АС ∙ ВМ . (2)

Складывая почленно равенства (1) и (2), получаем:

АВ ∙ DС+А D ∙ ВС=АС ∙ МD +АС ∙ ВМ,

АВ ∙ DС+АD ∙ ВС+АС ∙ ВD .

Теорема доказана.

По готовым чертежам сформулируйте и докажите следствия из теоремы Птолемея.

Следствие 1. Если трапеция равнобедренная, то

d = a∙b + c.

Следствие 2. Для любого прямоугольника справедливо равенство

d = a + b.

С помощью теоремы Птолемея можно доказать другие известные теоремы, например, теорему Пифагора (докажите ее самостоятельно на самоподготовке), теорему косинусов (обобщенную теорему Пифагора).

С помощью этой теоремы можно получить формулы синуса суммы и разности двух углов.

Попробуем решить с помощью теоремы Птолемея задачи из задания на самоподготовку.

Задача 1. Боковая сторона равнобедренной трапеции равна , а основания 3 и 4. Найдите длину диагонали трапеции.

Р е ш е н и е. Так как трапеция равнобедренная, то ее диагонали равны и около нее можно описать окружность.

По теореме Птолемея имеем

АС ∙ ВD = АВ ∙ СD + ВС ∙ А D, АС = ∙ + 3 ∙ 4, АС=5.

Ответ: 5.

.

Задача 2. Дан ромб АВСD. Окружность, описанная около треугольника АВD , пересекает большую диагональ ромба АС в точке Е. Найдите СЕ, если АВ= 8, ВD=16.

Р е ш е н и е. Диагонали ромба пересекаются в точке О. Из треугольника АОВ находим АО=16, следовательно, АС=32. Из треугольника АDЕ выражаем DЕ, DЕ=.

.Четырехугольник АВЕD вписан в окружность.

По теореме Птолемея

АЕ ∙ 16=8∙D Е+8∙ ВЕ, АЕ= DЕ,

АЕ= , АЕ=20,

следовательно, СЕ= АС – АЕ = 32 – 20 = 12.

Ответ: 12.

Задача 3. Около равностороннего треугольника описана окружность, и на дуге ВС взята произвольная точка М. Найдите длину отрезка АМ, если ВМ=26 см, СМ=14 см.

Р е ш е н и е. Четырехугольник АВМС вписанный, тогда по теореме Птолемея

АМ ВС=АВ МС+АС ВМ.

Так как треугольник АВС равносторонний, то АВ=ВС=АС= . Получим АМ = 14 + 26, АМ=40.

Ответ: 40.

Задача 4. На гипотенузе прямоугольного треугольника с катетами 3 см и 4 см построен квадрат, причем центр квадрата и вершина прямого угла лежат по разные стороны от гипотенузы. Найдите расстояние от центра квадрата до вершины прямого угла.

Р е ш е н и е. Опишем окружность около треугольника АВС. Окружность проходит через центр квадрата D (ADB=90). Четырехугольник АDВС вписан в окружность.

По теореме Пифагора найдем АВ:

АВ= АС+ВС, АВ=5см.

Так как АD=ВD= см, по теореме Птолемея

АВ ∙ CD +АС ∙ ВD + ВС ∙AD,

5∙ СD = 3∙ + 4 ∙, СD = 7∙ см.

Ответ: см.

Подведение итогов урока.

Самоподготовка.

Задача1. Большее основание равнобедренной трапеции равно 8, боковая сторона равна 9, а диагональ равна 11. Найдите меньшее основание трапеции.

Ответ: 5.

Задача 2.

*Докажите теорему Пифагора с помощью теоремы Птолемея.

2′

10′

28′

5`

Суворовцы задают друг другу вопросы

и отвечают на них.

Суворовцы

отвечают у доски, демонстрируют на документ- камере решенные на самоподготовке задачи.

Суворовец

рассказывает о

о жизни и творчестве Птолемея, показывает презентацию.

Доказательства подобия треугольников суворовцы сам-но отвечают у доски.

Суворовцы конспектируют

в теоретической тетради.

Суворовцы

Самостоятельно формулируют и доказывают

Свойства.

Суворовцы

решают задачи в рабочих тетрадях

и на доске.

Суворовцы записывают задание на самоподготовку.