Конспект урока «Сложение рациональных чисел с разными знаками» по математике

Тема: Сложение рациональных чисел с разными знаками.

Цели урока:

1. Сформулировать правило сложения чисел с разными знаками; научить определять знак суммы сложения чисел с разными знаками; развивать умения и навыки работы с операциями сложения чисел с разными знаками.

2. Развивать предметные и общеучебные навыки и умения, умение использовать полученные знания для достижения поставленной цели; устанавливать закономерности многообразия связей для достижения уровня системности знаний.

3. Воспитание навыков самоконтроля ; самостоятельность, интерес к предмету.

Ход урока.

1. Организационный момент.

Девизом к сегодняшнему уроку будут слова древнегреческого математика Фалеса:

- Что есть больше всего на свете? – Пространство.

- Что быстрее всего? – Ум.

- Что мудрее всего? – Время.

- Что приятнее всего? – Достичь желаемого.

Хочется, чтобы каждый из вас на сегодняшнем уроке достиг желаемого результата.

Сегодня на уроке, ребята, нам предстоит выполнить серьёзную работу. От вас потребуется усидчивость, стремление, внимание, последовательность и правильность выполнения заданий. Сегодня мы познакомимся со сложением рациональных чисел с разными знаками.

2. Мотивация урока.

“Недостаточно овладеть правилом,

Нужно так же уметь пользоваться им.”

Цицерон

Обсудить высказывание с учащимися.

Вывод: недостаточно знать правила, надо уметь их применять.

3. Актуализация опорных знаний.

Какие числа называются положительными? отрицательными?

Какое число не положительно и не отрицательное?

- Дать определение положительного числа и выбрать их.

- Дать определение отрицательного числа и выбрать их.

- Есть ли среди этих чисел противоположные? Дать определение.

- К каким числам относится число 0?

- Что такое координатная прямая?

- Где на координатной прямой расположены положительные числа?

- Отрицательные?

Что такое модуль числа?

Какую тему мы проходим?

Еще не зная про отрицательные числа мы уже встречались в жизни с ними, в каких ситуациях?

Как располагаются положительные и отрицательные числа на координатной прямой?

Как начертить координатную прямую?

Какое число называется отрицательным?

Что называется модулем числа?

Модуль какого числа больше: -3 или 2; -6 или –4. А какое число больше?

Модуль какого числа равен –20?

К числам 8, -4, 2/3, 0 подберите противоположные и обратные.

Какие числа мы называем рациональными?

С какими числами люди познакомились сначала и почему возникли другие числа?

-(-11), +(-7), -(+3)

Что больше и почему: 0 или 7; 3 или 29?

1) Если модуль числа больше самого числа, то оно отрицательное.

2) Если модуль равен этому числу, то оно равно 0.

3) На координатной прямой между числами -4,5 и -2 лежат 2 целых числа.

4) Из двух чисел с разными знаками больше то, у которого модуль больше.

5) -4,5555 > - 4,5.

6) Если –х>0, то х

7) Если х, то оно неотрицательно.

8) Большее из двух положительных чисел имеет больший модуль.

9) Любое отрицательное число меньше положительного.

10) Нуль больше любого неотрицательного числа.

1) Как сложить два отрицательных числа?

Устный счет:

– 15 + (- 12) =

– 15,5 + (- 14,5) =

– 2,8 + (- 17,2) =

- 15 + (- 3) =

– 49 + (- 18,4) =

– 100 + (- 48,6) =

4 . Разбор нового материала

А как ребята, можно догадаться как это считать, не пользуясь координатной прямой и термометром?

8+(-5)=3

4+(-10)= -6

А какое число имеет больший модуль? А теперь скажите, какой знак получится у суммы при сложении чисел с разными знаками?

12+(-5)=7

8+(-11)= -3

Попробуем сформулировать правило.

Чтобы сложить два числа с разными знаками надо:

• из большего модуля вычесть меньший модуль;

• поставить перед полученным числом знак слагаемого с большим модулем.

-7+4=-3, 6+(-2)=4.

Запомнить: а+(-а)=0.

-3+3=0.

5. Решение упражнений.

Решить №.446 устно № 449, 450, 451

Историческая пауза.

Индийские математики Брамагупта (VII век) и Бхаскара (XII век) с помощью положительных чисел выражали имущество, а с помощью отрицательных “долг”. Они составили правила действий для этих чисел. Однако долгое время отрицательные числа считали не настоящими, фиктивными, абсурдными.

В Европе к отрицательным числам обращается итальянский математик Леонардо Фибоначчи, но в учении об отрицательных числах далее продвинулся М.Штифель (XVI век). Отрицательные числа он называл как “меньше чем ничто” и говорил, что нуль находится между истинными и абсурдными числами. И только после работ выдающегося ученого Р.Декарта (XVII век) и других ученых (XVII – XVIII века) отрицательные числа приобрели “права гражданства”.

5. Самостоятельная работа.

1. Выбери верное утверждение: х > 0, если

А. х - любое целое число; В. х - дробное;

С. х - натуральное; D. х - рациональное.

2. Укажи верное неравенство.

А. -7 В. -8 > -18; С. -5,7 D. -36 > -1.

3. Укажи наименьшее по модулю число.

А. -13,97; В. 6,3; С. -53,8; D. -2.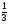

4. Укажи наибольшее по модулю число.

А. -13,97; В. 6,3; С. -53,8; D. -2.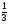

5. Выбери верное неравенство, если а – положительное, в –

отрицательное:

А. –а > в; В. –в 0; D. –а

6. Выбери наименьшее число. А. -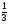; В. 2; С. -; D. -.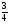

7. Выбери наибольшее число. А. -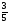; В. -1; С. -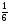; D. -.

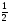8. Определи знаки чисел в значении суммы:

-85+34; 25+(-19); 76+(-35); 19+(-25).

А. - - + +; В. + - + -; С. - + + -; D. - + - +.

9. Выполни действия:

-19+40 А. 59; В. 21; С. -59; D. -21.

-3,4+5,7 А. 9,1; В. 2,3; С. -2,3; D. -9,1.

10. Сколько целых чисел удовлетворяют неравенству -8

А. 12; В. 10; С. 11; D. 9.

11. Вычислите: |-7,7 + 5,2|. А. -2,5; В. 2,5; С. 12,9; D. -12,9.

6. Подведение итогов урока. Д/з. п 3.2 № 448 стр 107

Рефлексия.

- Что нового для себя узнали?

- В чём затруднялись?

- Чему научились?

- Какую проблему ставили на уроке?

- Удалось ли нам её решить?

Устный счет:

– 22 + 35 =

– 3,7 + 2,8 =

1,5 + (- 6,3) =

8,2 + (-8,2)=

22+(– 27)=

– 13+(– 8)=

19+ (- 2)=

27 + (- 3) =

-35 + 9=

-1,6 +(-4,7)=

2,5+(-3,6)=

Сравните (вместо звездочки поставьте знаки =, )

– 5,6 + 1,8 * – 3,8;

– 5,6 + 1,8 * 3,8;

– 5,6 + (– 1,8) * – 3,8.

6. Подведение итогов урока. Рефлексия. Д/з. № 454 стр 108

• Какие правила вы сегодня повторили?

• Какие умения вы сегодня отрабатывали?

• Что нового вы узнали сегодня на уроке?

!! – Я хорошо знаю правила (решаю примеры практически без ошибок)

!? – Я не совсем уверен в знаниях (допускаю ошибки)

?? – Мне еще нужно повторить правила (допускаю много ошибок)

Выучить п. 34, повторить п. 3, решить № 984 , 986, 988(а).

Если числа с разными знаками дадут,

Чтоб найти их сумму, все мы тут как тут.

Больший модуль быстро очень выбираем

Из него мы меньший модуль вычитаем

Самое же главное – знак не позабыть!

- Вы какой поставите? – мы хотим спросить.

- Вам секрет откроем. Проще дела нет,

Знак, где модуль больше, запиши в ответ.

1. Что нового вы узнали, чему научились, что вспомнили, повторили?….

2. Чьи ответы вам понравились больше всего?

3. Что запомнится надолго после сегодняшнего урока?

4. Ваши впечатления об уроке. Эмоциональный настрой.

Решить № 461, 466 стр 110