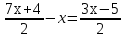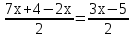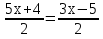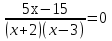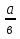Конспект урока «Уравнения с одной переменной. Равносильность уравнений» по математике

Деятельность учителя

Деятельность студента

Орг.момент

Актуализация знаний.

Решение заданий

Итог урока.

Д.з.

Здравствуйте, садитесь. Сегодня мы с вами повторим все необходимые знания, нужные для того, чтобы решить уравнение с одним неизвестным.

1. Вам было дано задание подготовить наглядность для актуализации знаний по теме «Уравнение» в начальной школе. Вы сейчас покажете свои работы, а затем мы посмотрим, как это можно сделать с помощью компьютера.

(слайды 2-6)

2. Ответьте на вопросы:

- Что называется уравнением?

Слайд 7

- Что значит решить уравнение?

- Корнем уравнения?

Слайд 8

– Проверьте, является ли -4 корнем уравнения

Х-0,59х-120=13-0,25х

3)Как называется уравнение вида ax = b

4) Как находят корни такого уравнения?

5)Сколько корней имеет уравнение 3(х-2)+2х-11=5х+3?

6)Какие уравнения называются равносильными.

7)Выяснить, равносильны ли уравнения (х+1)² =9 и

(х-2)(х+4)=0

Какие теоремы и следствия из них позволяют получать уравнения, равносильные исходному?

(слайд9, 10, 11,12)

1. Решите уравнения из №5, стр. 258.

Прочитайте задание. Решите уравнение и объясните, какие теоретические положения были при этом использованы

1)

2)5х+4 =3х -5

3. Выражение 3х переносим в левую часть, а 4 - в правую: 5х-3х = -5-4

4. Привели подобные слагаемые: 2х = -9

5. Разделили обе части уравнения на 2: х=-4,5

2. Рассмотрим уже решённое уравнение

х(х-1) =2х

х (х-1) = 2х

х-1 = 2

х = 3

(Слайд 13)

Верно ли решено уравнение? Все ли корни найдены?

Но мы его потеряли. Почему?

Как правильно решить это уравнение?

3. Решите уравнение

Самостоятельная работа – Решите уравнения различными способами

1) (х-1) +3(х-1)=0

2)(х+1)(х-2)+(х-2)(х+4)=6(2х+5)

П.97 с заданиями.

Урок окончен!

Студенты показывают свою домашнюю работу и рассказывают о ней.

1. Уравнение – это равенство, содержащее переменную.

2. Читают второе определение со слайда.

3)Решить уравнение –значит найти все его корни или доказать, что корней нет.

4)Корнем уравнения называется такое значение переменной, при котором уравнение обращается в верное равенство.

-Нет (подставляют в уравнение вместо х число -4)

- линейное

Если а≠0 и в≠0, х=

Если а= 0, а в≠ 0, уравнение не имеет корней.

Если а=0 и в = 0, уравнение имеет бесконечное множество корней.

3х-6+2х-11=5х+3

3х-5х +2х= 3+6+11

0х=20

Нет корней.

Два уравнения называются равносильными, если их множества решений равны.

Решают уравнения разными способами.

1)

1. х+1 =3 или х+1=-3

х=2 х=-4

2. х² +2х +1 =9

х² +2х -8 = 0

д=36

х₁ =2 х_{2 =}-4

2)х-2=0 или х+4=0

х=2 х= -4

Равносильны.

Теорема1. Пусть уравнение f(x)=g(x) задано на множестве Х и h(x)- выражение, определённое на том же множестве. Тогда уравнения

f(x)=g(x) и f(x)+h(x) =g(x) +h(x)

равносильны на множестве Х.

Следствие 1. если к обеим частям уравнения прибавить или отнять одно и тоже число, то получится уравнение равносильное исходному.

Следствие 2. Если какое-либо слагаемое (числовое выражение или выражение с переменной) перенести из одной части уравнения в другую, поменяв знак слагаемого на противоположный, то получим уравнение, равносильное данному.

(Читают задание, затем выполняют, используя правила и образцы из учебника)

Выполним тождественные преобразования в левой части, получили уравнение равносильное исходному.

Домножим обе части уравнения на 2, получили уравнение равносильное предыдущему, а значит исходному.

Воспользовались следствием из теоремы 1, получили уравнение равносильное предыдущему, а значит исходному.

Выполним тождественные преобразования, получили уравнение равносильное предыдущему, а значит исходному.

Воспользовались следствием из теоремы 2, получили уравнение равносильное предыдущему, а значит исходному.

- Нет, так как при х=0 уравнение также обращается в верное равенство. 0- корень уравнения.

- Домножили на 1/х, которое определено не для всех х, например при х = 0, оно не имеет смысл.

Решают различными способами.

х(х-1) -2х = 0 х (х-1) = 2х

х(х-1-2) = 0 х² –х -2х =0

х=0 или х-3=0 х² -3х =0

х=3 х=0 или х-3=0

х=3

Домножим его на знаменатель (х+2)(х-3)≠0. Получим

5х-15 =0

Х=3.

Но при х=3 знаменатель обращается в нуль, т.е. х=3 не может быть корнем. Значит уравнение не имеет корней.