Слайд 1Углы в пространстве
Автор Календарева Н.Е. © 2011 г.
Слайд 2План
Угол между прямыми Решение задач Угол между прямой и плоскостью Решение задач Двугранный угол Линейный угол двугранного угла Угол между плоскостями
Слайд 3Угол между прямыми
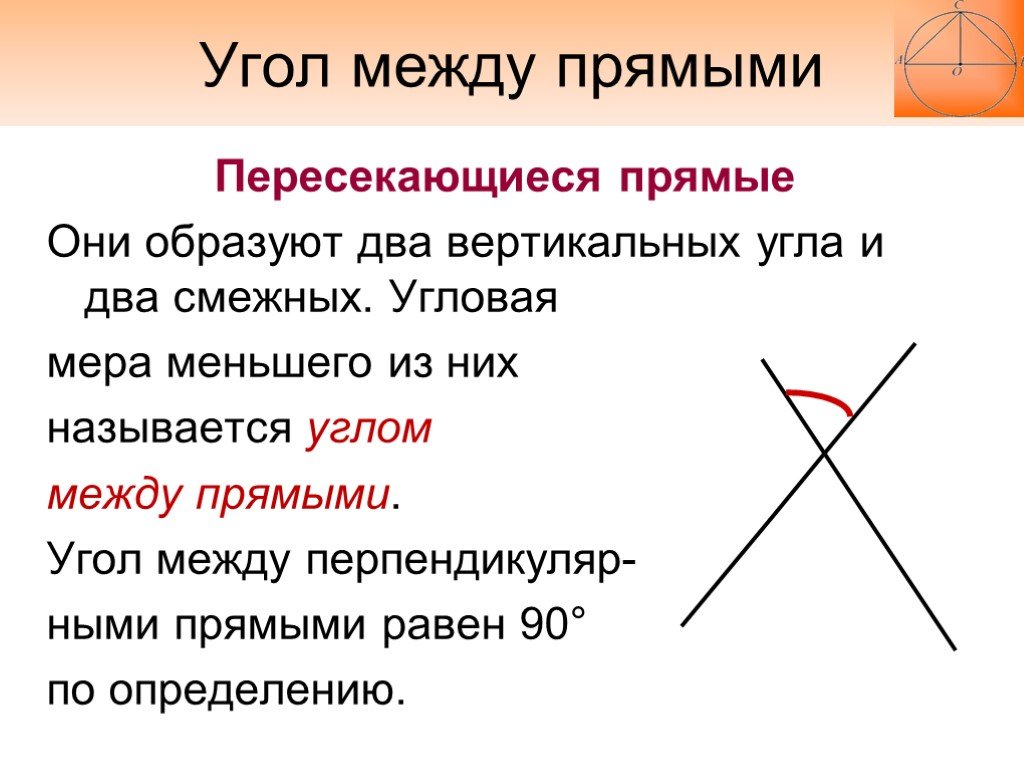
Пересекающиеся прямые Они образуют два вертикальных угла и два смежных. Угловая мера меньшего из них называется углом между прямыми. Угол между перпендикуляр- ными прямыми равен 90° по определению.
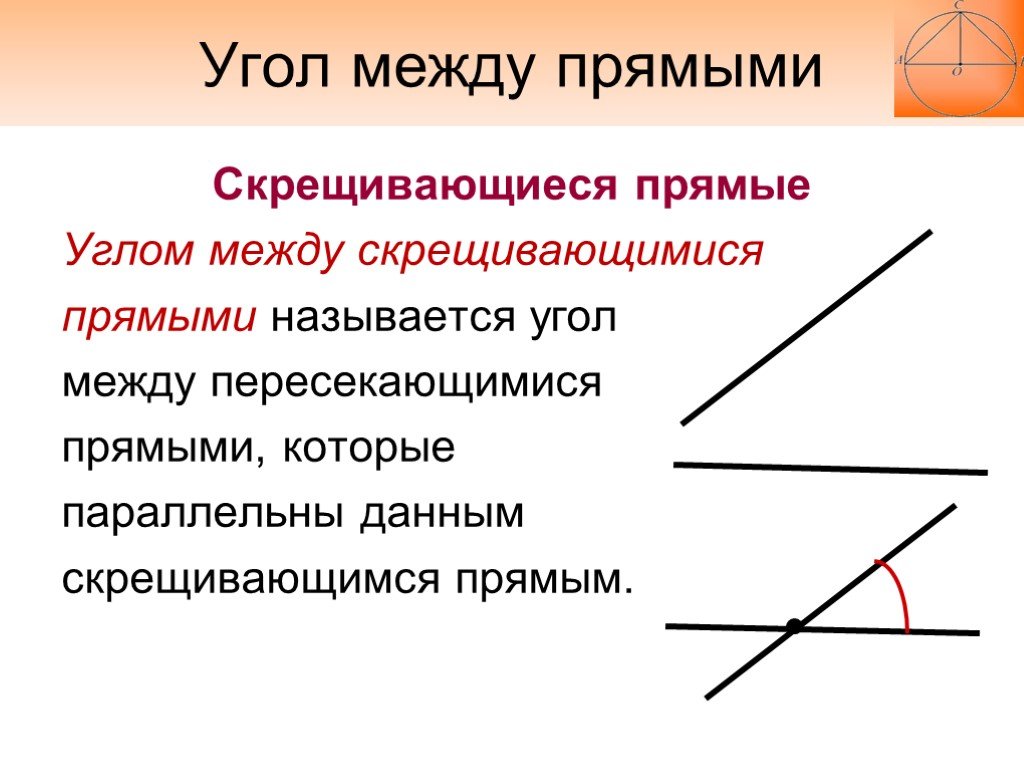
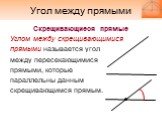
Слайд 4Скрещивающиеся прямые Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, которые параллельны данным скрещивающимся прямым.
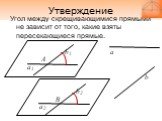
Слайд 5Утверждение
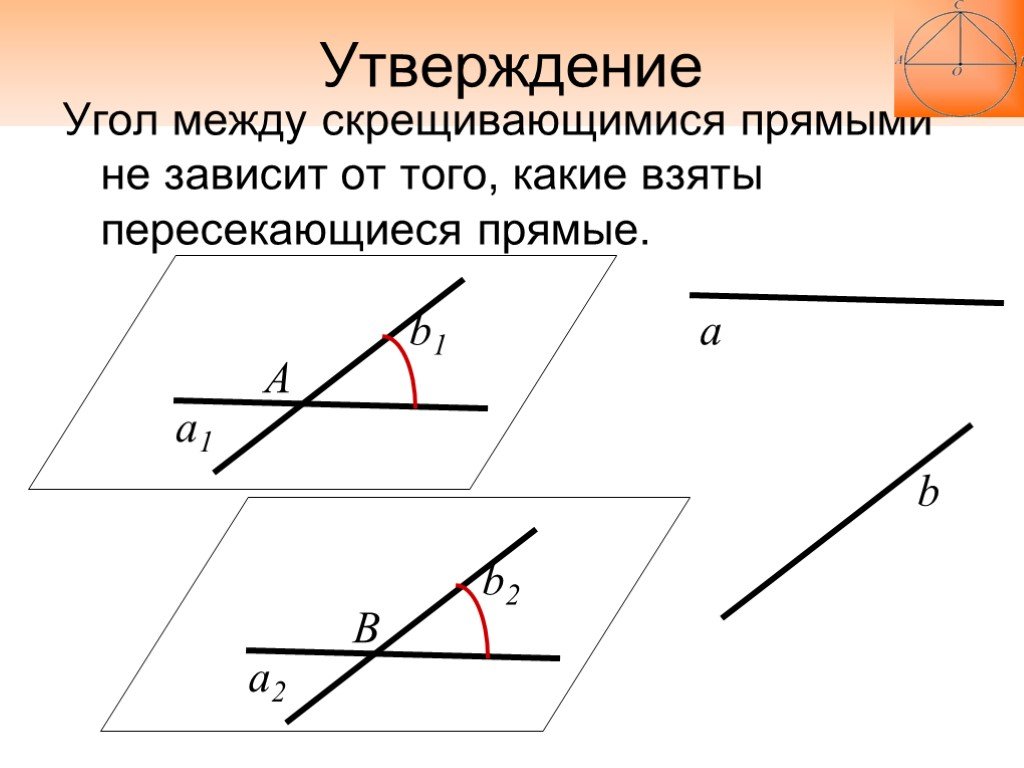
Угол между скрещивающимися прямыми не зависит от того, какие взяты пересекающиеся прямые.
Слайд 6Доказательство
По теореме «Две прямые, параллельные третьей, параллельны» прямые а1 и а2 параллельны (или совпадают) и прямые b1 и b2 параллельны (или совпадают). Выполним параллельный перенос, при котором точка А переходит в точку В. При этом параллельном переносе прямая а1 переходит в а2, прямая b1 – в b2. Углы при парал. переносе сохраняются.
Слайд 7Перпендикулярные прямые По определению перпендикулярными прямыми называются прямые, пересекающиеся под прямым углом. Если угол между скрещивающимися прямыми равен 90°, то эти прямые также называются перпендикулярными.
Слайд 8Параллельные прямые Угол между параллельными прямыми по определению равен 0. Итак, величина угла между прямыми в пространстве изменяется от 0 до 90° или от 0 до π/2 включительно.
Слайд 9Как решать задачи
Чтобы найти угол между прямыми, надо найти его тригонометрическую функцию (любую!). Если это табличное значение, то угол может быть выражен в градусах или в радианах. Тригонометрическую функцию надо находить из треугольника, для чего его надо достроить.
Слайд 10Для удобства делают так называемый «выносной» рисунок. На нем изображают треугольник правдоподобным, как в планиметрии. Находят и выносят на рисунок длины сторон треугольника.
Слайд 11Затем проверяют, является ли треугольник равносторонним; равнобедренным; прямоугольным. Если прямоугольный, то используем формулы для синуса или косинуса. Если равнобедренный или произвольный, то находим косинус угла по теореме косинусов.
Слайд 12Задача 1
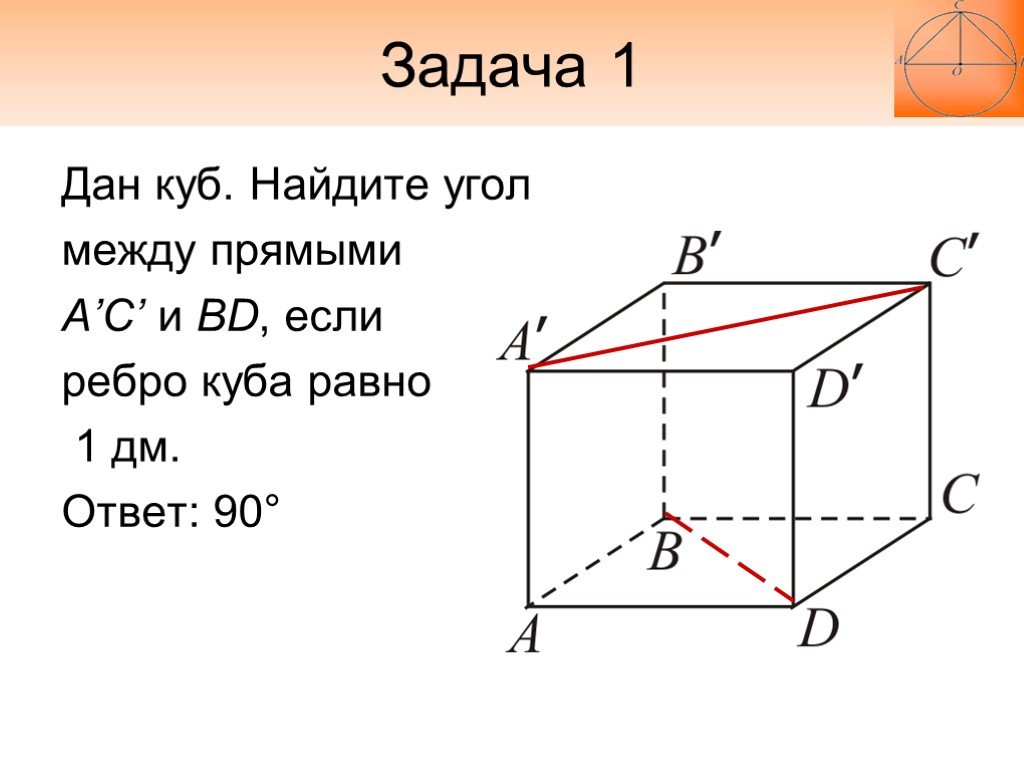
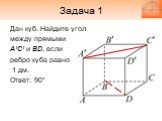
Дан куб. Найдите угол между прямыми A’C’ и BD, если ребро куба равно 1 дм. Ответ: 90°
Слайд 13Задача 2
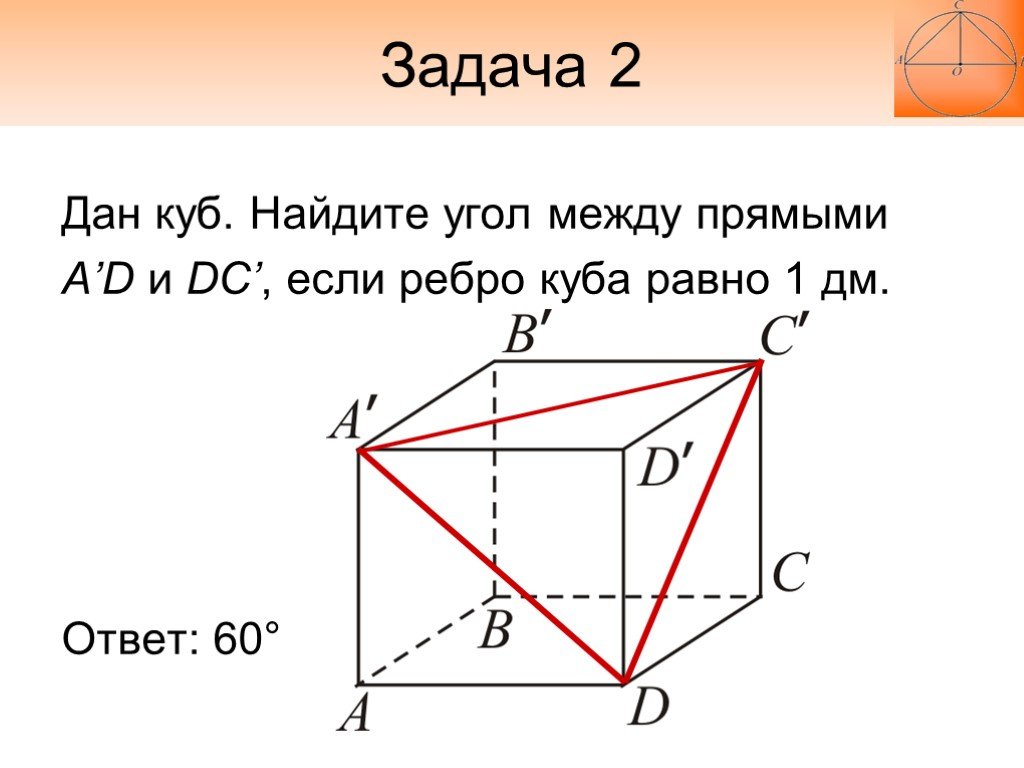
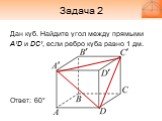
Дан куб. Найдите угол между прямыми A’D и DC’, если ребро куба равно 1 дм. Ответ: 60°
Слайд 14Задача 3
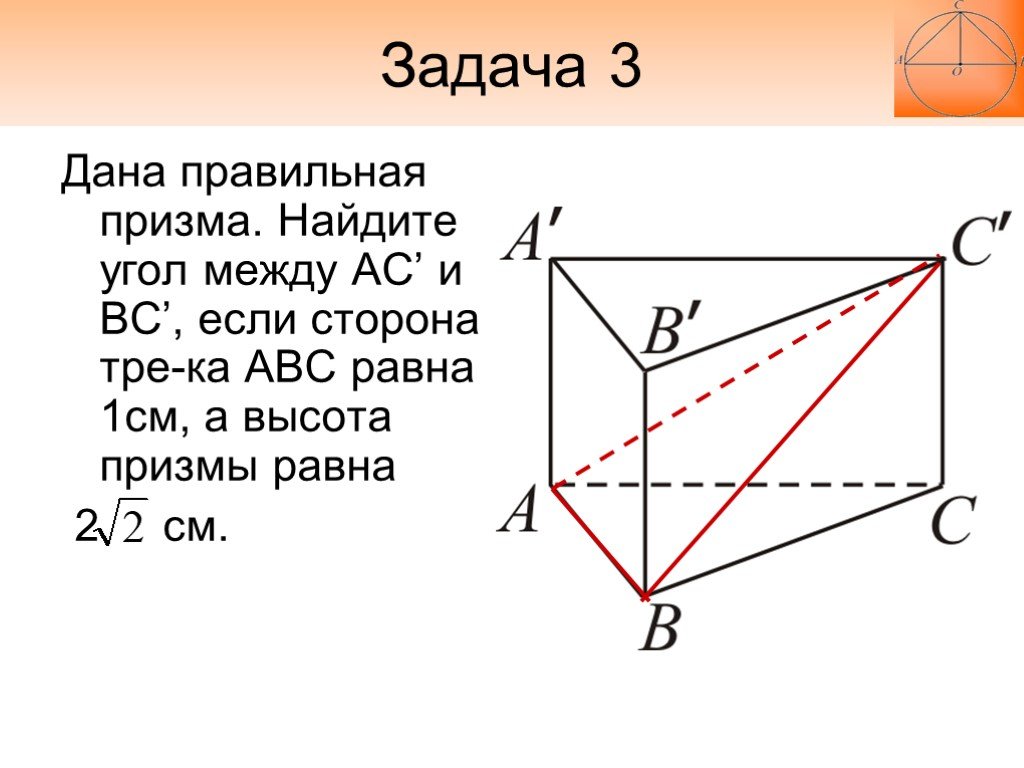
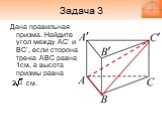
Дана правильная призма. Найдите угол между AC’ и BC’, если сторона тре-ка АВС равна 1см, а высота призмы равна 2 см.
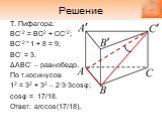
Слайд 15Решение
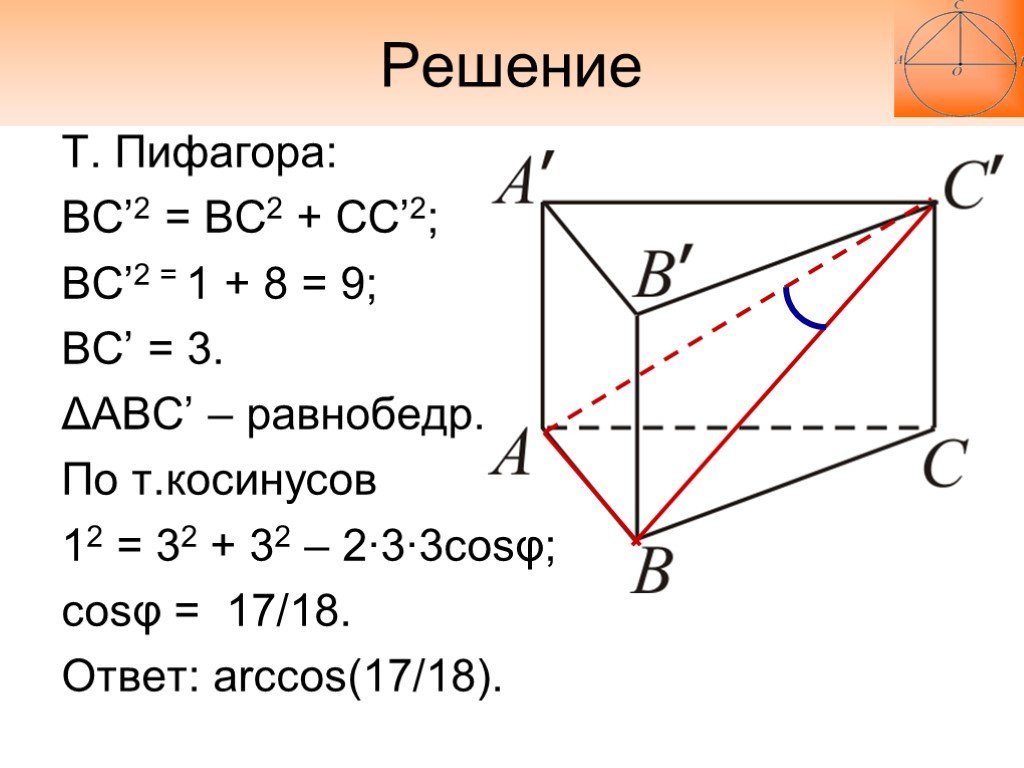
Т. Пифагора: BC’2 = BC2 + CC’2; BC’2 = 1 + 8 = 9; BC’ = 3. ΔABC’ – равнобедр. По т.косинусов 12 = 32 + 32 – 2∙3∙3cosφ; cosφ = 17/18. Ответ: arccos(17/18).
Слайд 16Угол между прямой и плоскостью
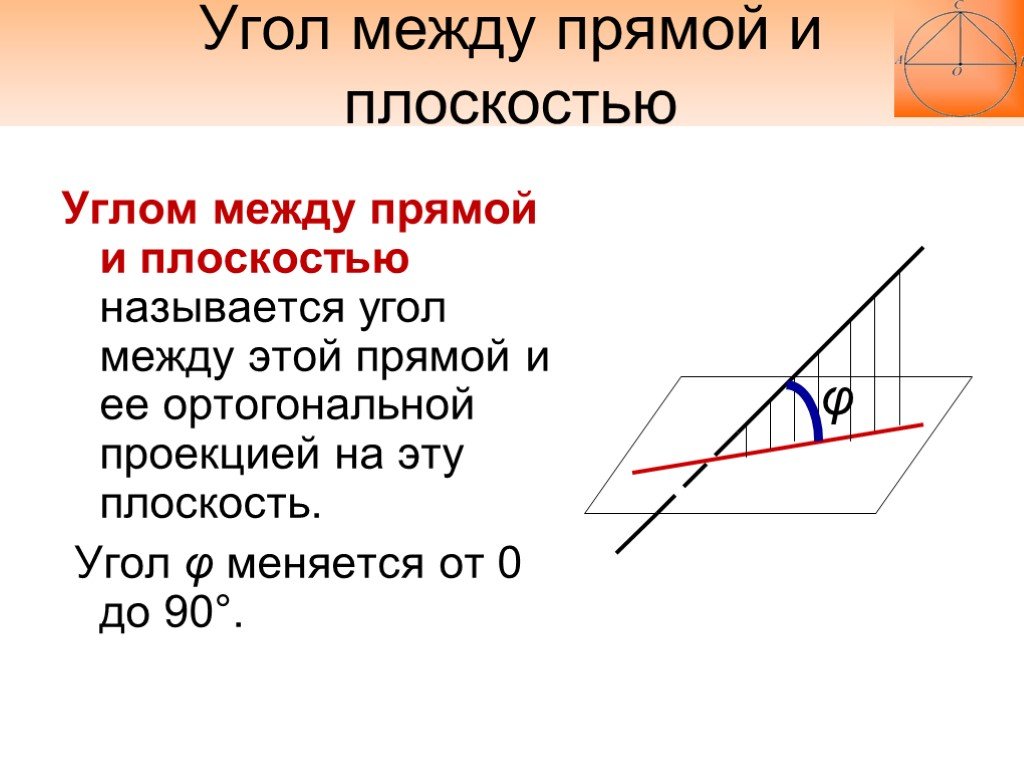
Углом между прямой и плоскостью называется угол между этой прямой и ее ортогональной проекцией на эту плоскость. Угол φ меняется от 0 до 90°.
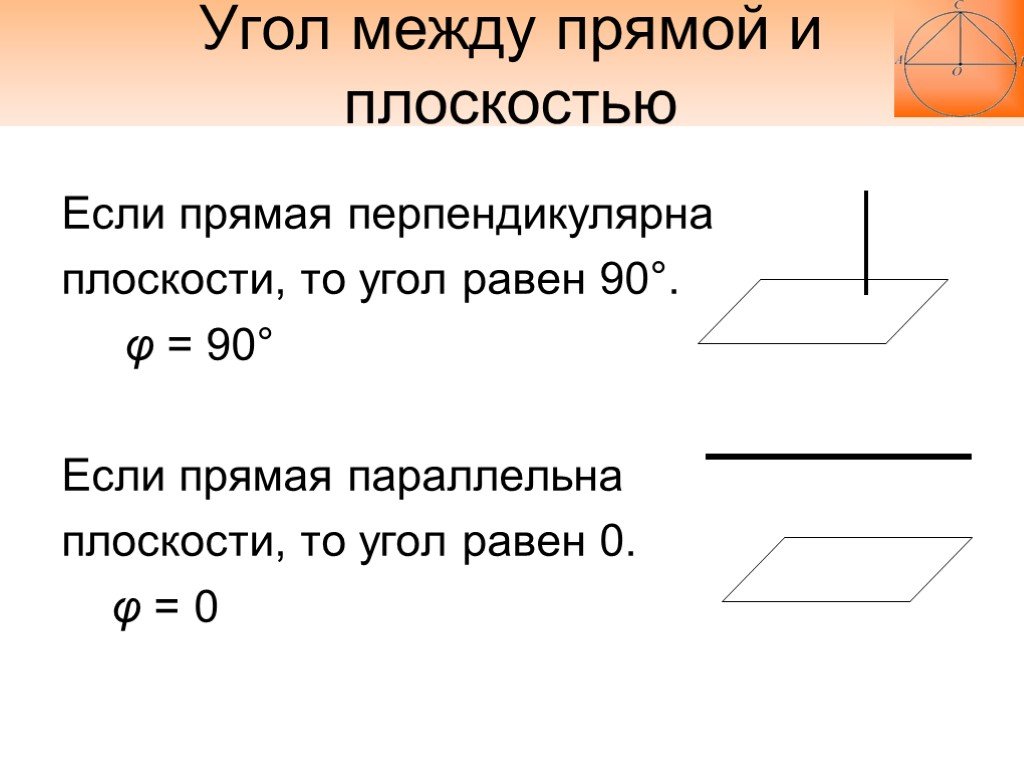
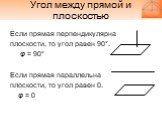
Слайд 17Если прямая перпендикулярна плоскости, то угол равен 90°. φ = 90° Если прямая параллельна плоскости, то угол равен 0. φ = 0
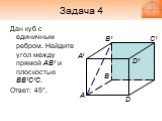
Слайд 18Задача 4
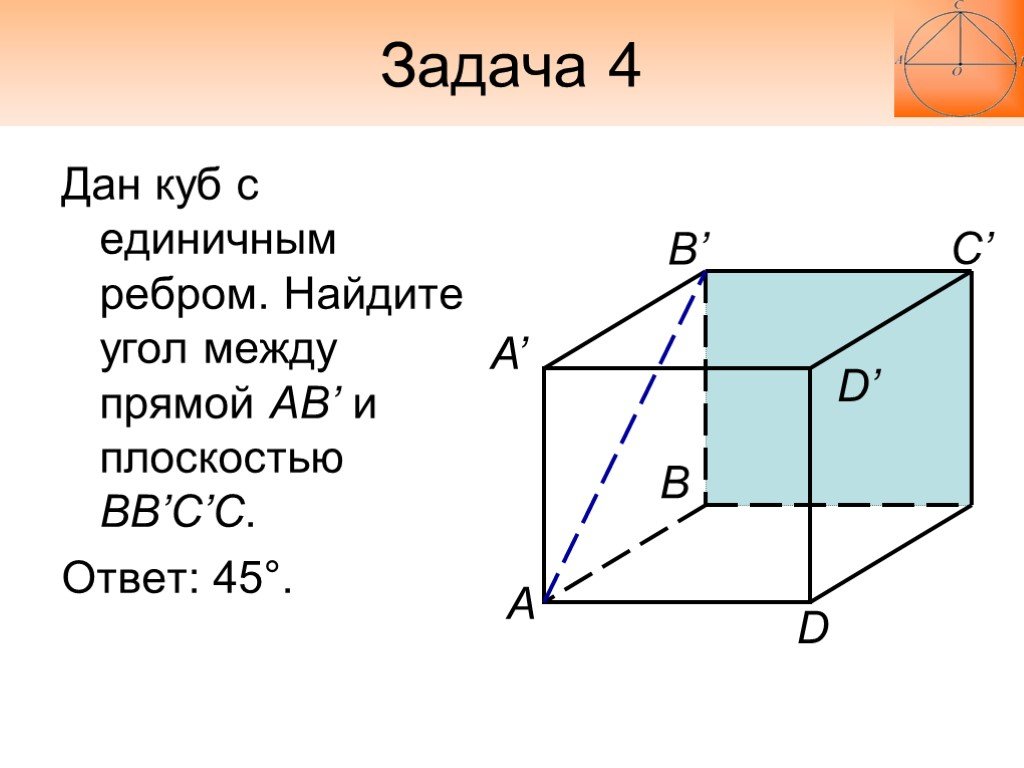
Дан куб с единичным ребром. Найдите угол между прямой АВ’ и плоскостью BB’C’C. Ответ: 45°.
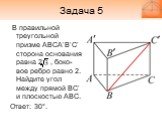
Слайд 19Задача 5
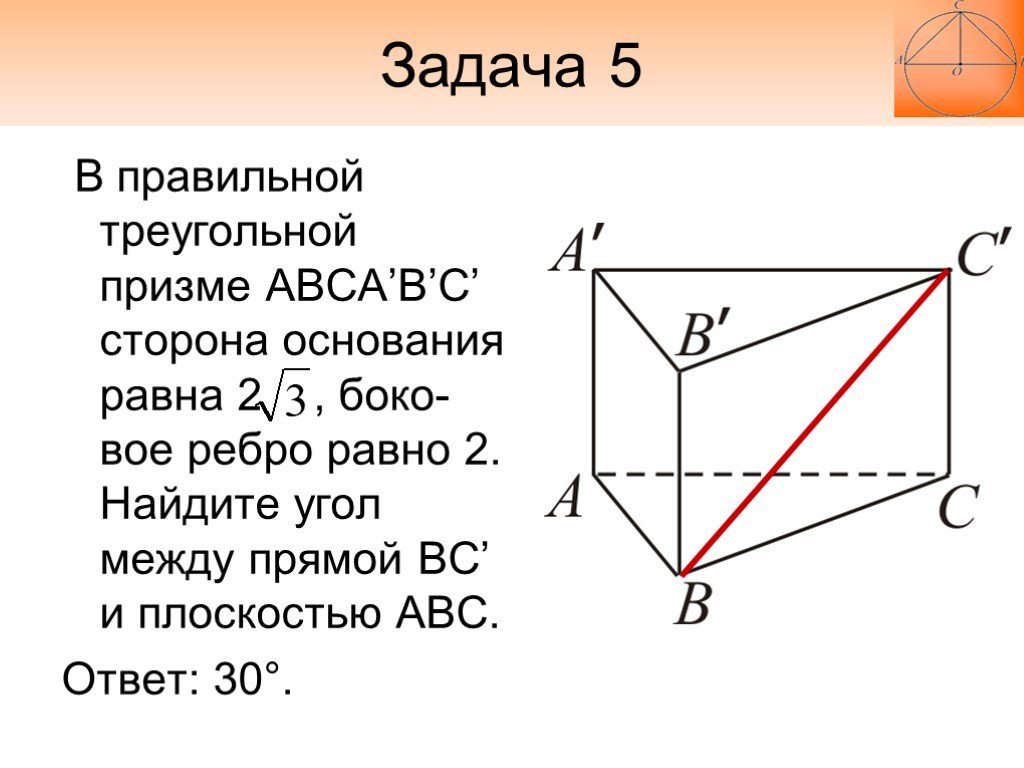
В правильной треугольной призме ABCA’B’C’ сторона основания равна 2 , боко-вое ребро равно 2. Найдите угол между прямой BC’ и плоскостью ABC. Ответ: 30°.
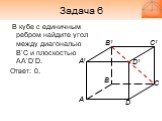
Слайд 20Задача 6
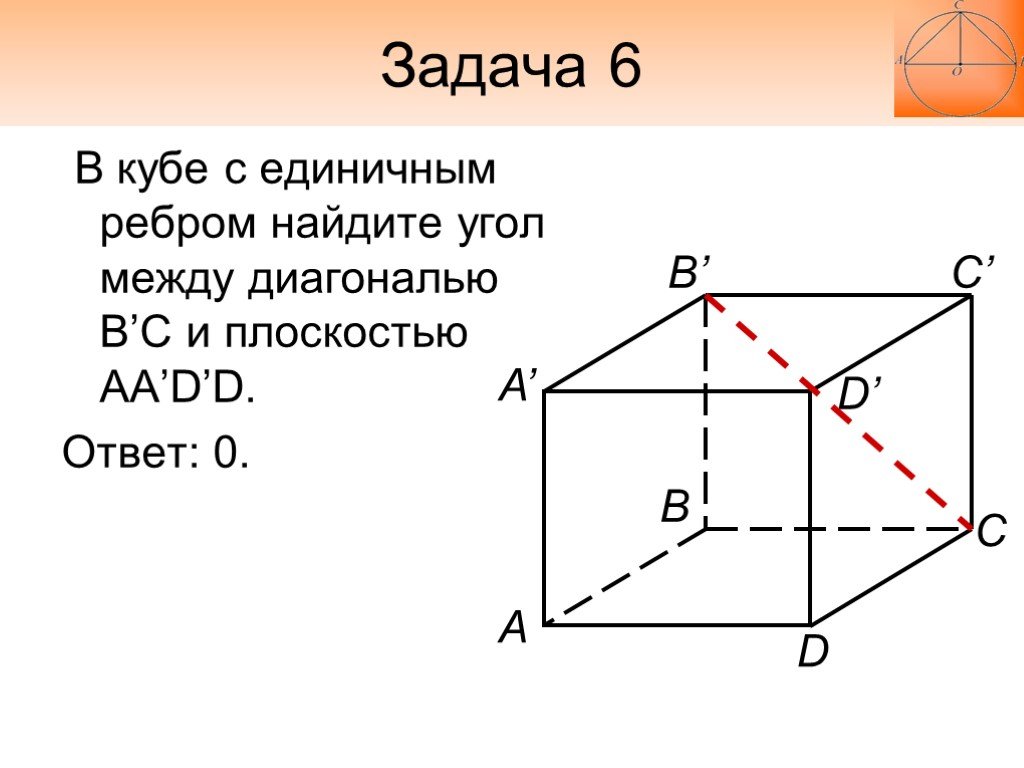
В кубе с единичным ребром найдите угол между диагональю B’C и плоскостью AA’D’D. Ответ: 0.
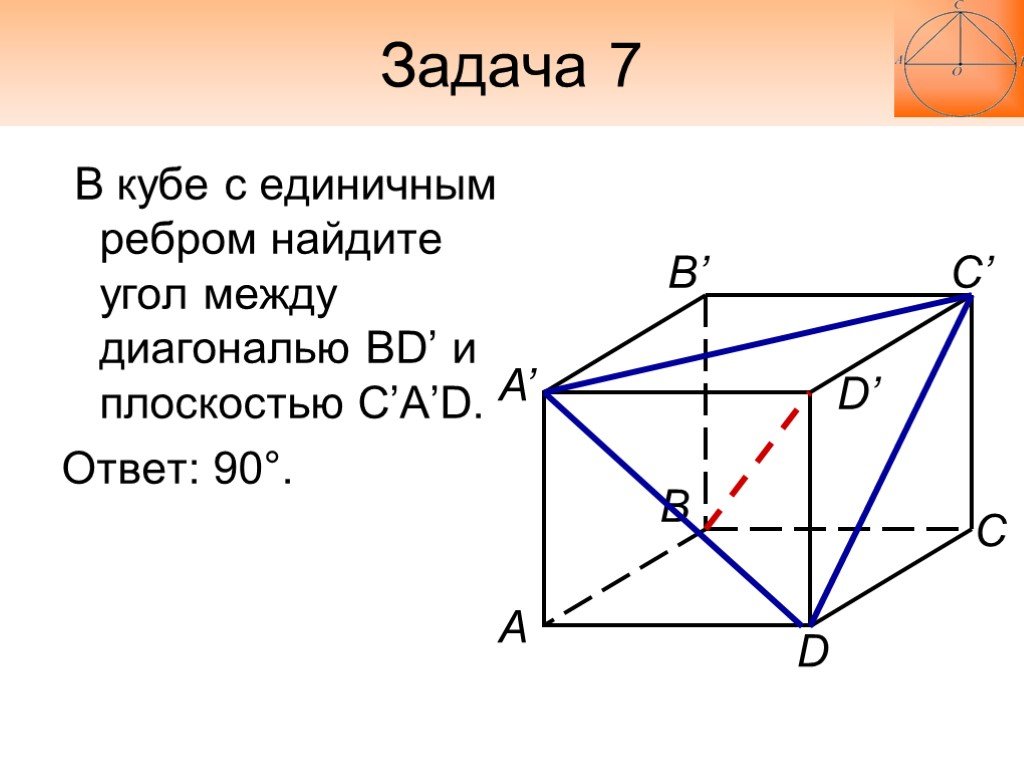
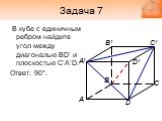
Слайд 21Задача 7
В кубе с единичным ребром найдите угол между диагональю BD’ и плоскостью C’A’D. Ответ: 90°.
Слайд 22Двугранный угол
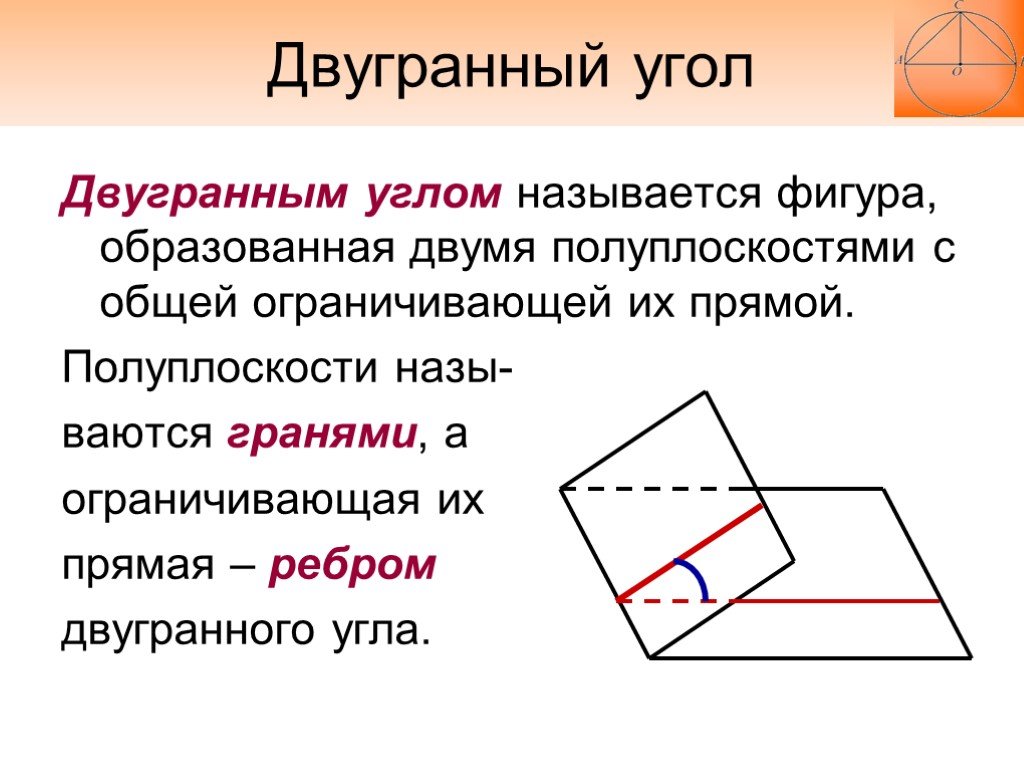
Двугранным углом называется фигура, образованная двумя полуплоскостями с общей ограничивающей их прямой. Полуплоскости назы- ваются гранями, а ограничивающая их прямая – ребром двугранного угла.
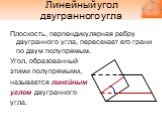
Слайд 23Линейный угол двугранного угла
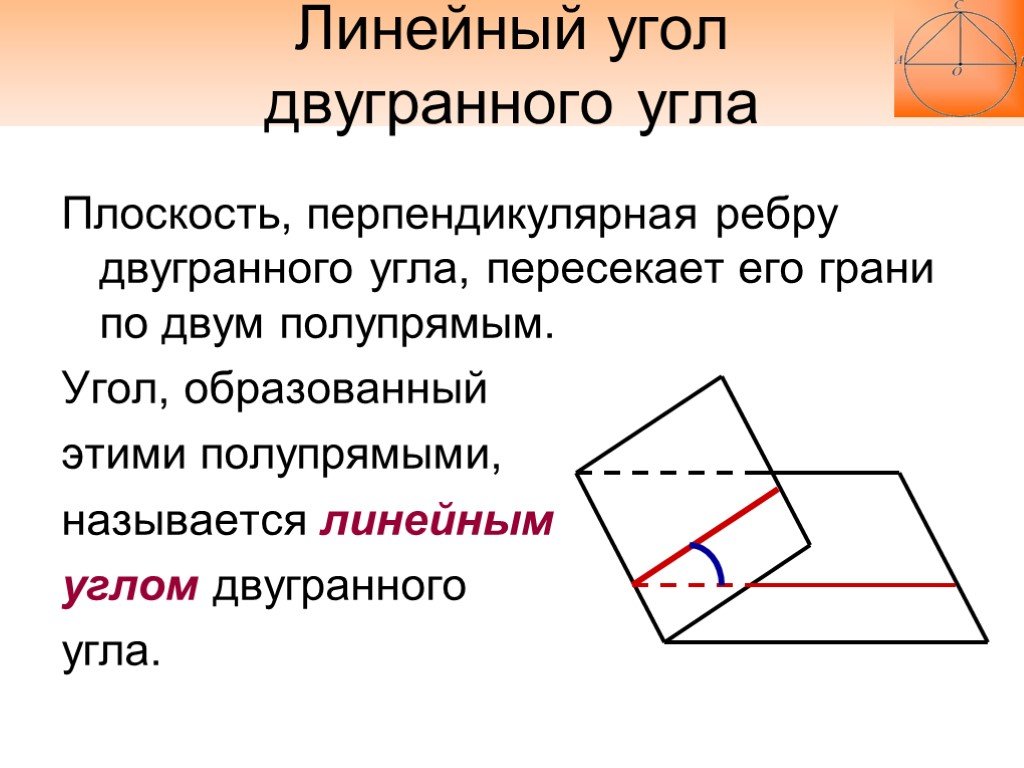
Плоскость, перпендикулярная ребру двугранного угла, пересекает его грани по двум полупрямым. Угол, образованный этими полупрямыми, называется линейным углом двугранного угла.
Слайд 24Мера двугранного угла
За меру двугранного угла принимается градусная или радианная мера соответствующего ему линейного угла. Все линейные углы двугранного угла совмещаются параллельным переносом, а значит, равны. Поэтому мера двугранного угла не зависит от выбора линейного угла.
Слайд 25Трехгранный угол
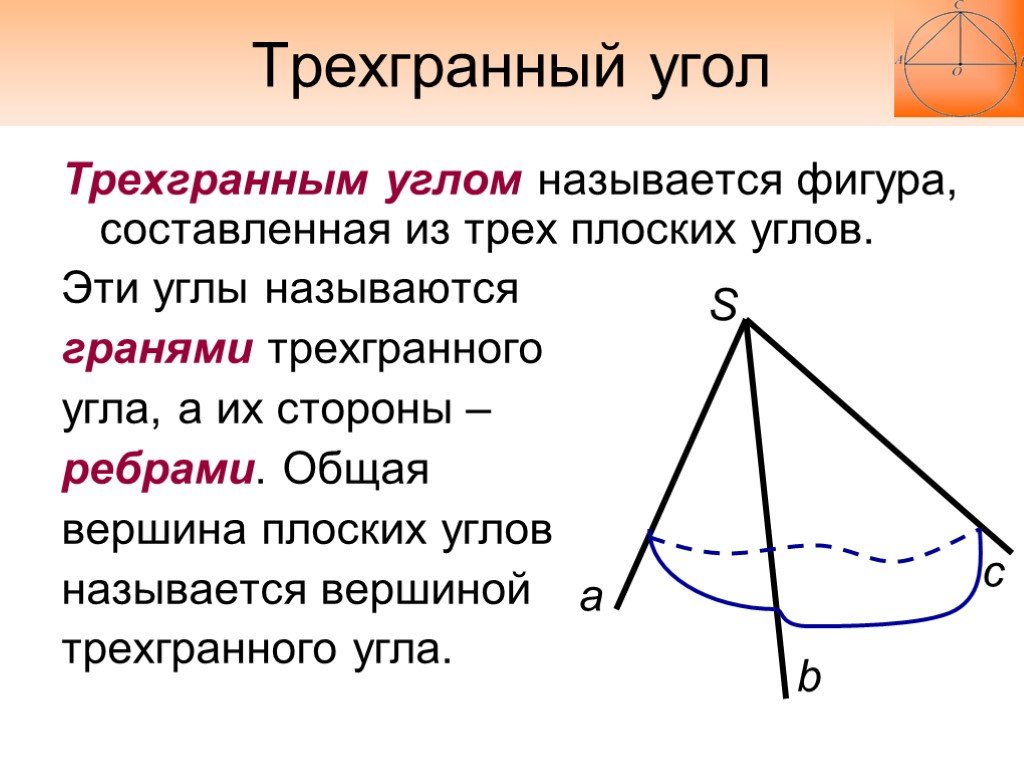
Трехгранным углом называется фигура, составленная из трех плоских углов. Эти углы называются гранями трехгранного угла, а их стороны – ребрами. Общая вершина плоских углов называется вершиной трехгранного угла.
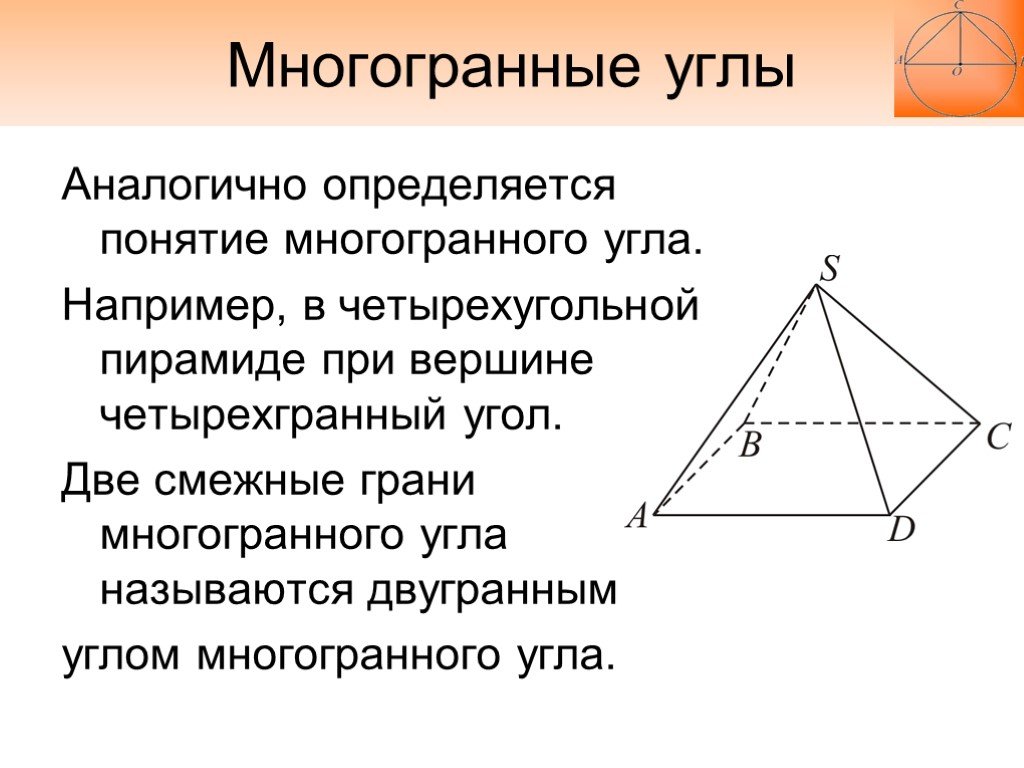
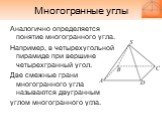
Слайд 26Многогранные углы
Аналогично определяется понятие многогранного угла. Например, в четырехугольной пирамиде при вершине четырехгранный угол. Две смежные грани многогранного угла называются двугранным углом многогранного угла.
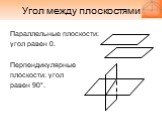
Слайд 27Угол между плоскостями
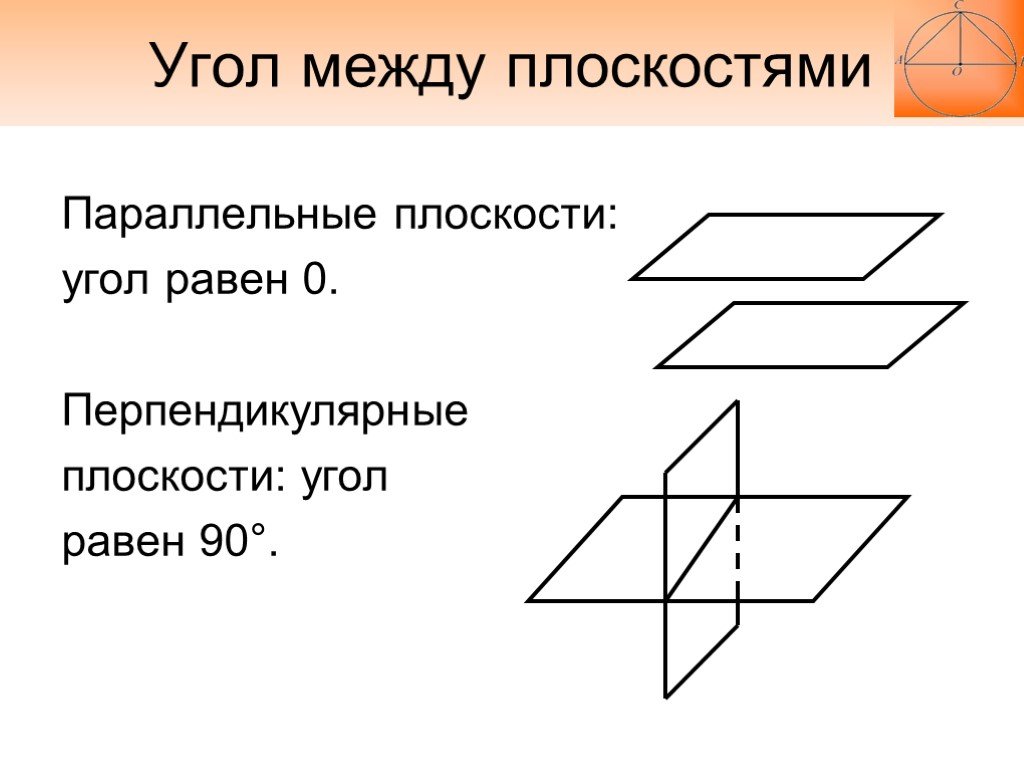
Параллельные плоскости: угол равен 0. Перпендикулярные плоскости: угол равен 90°.
Слайд 28Угол между пересекаю- щимися плоскостями
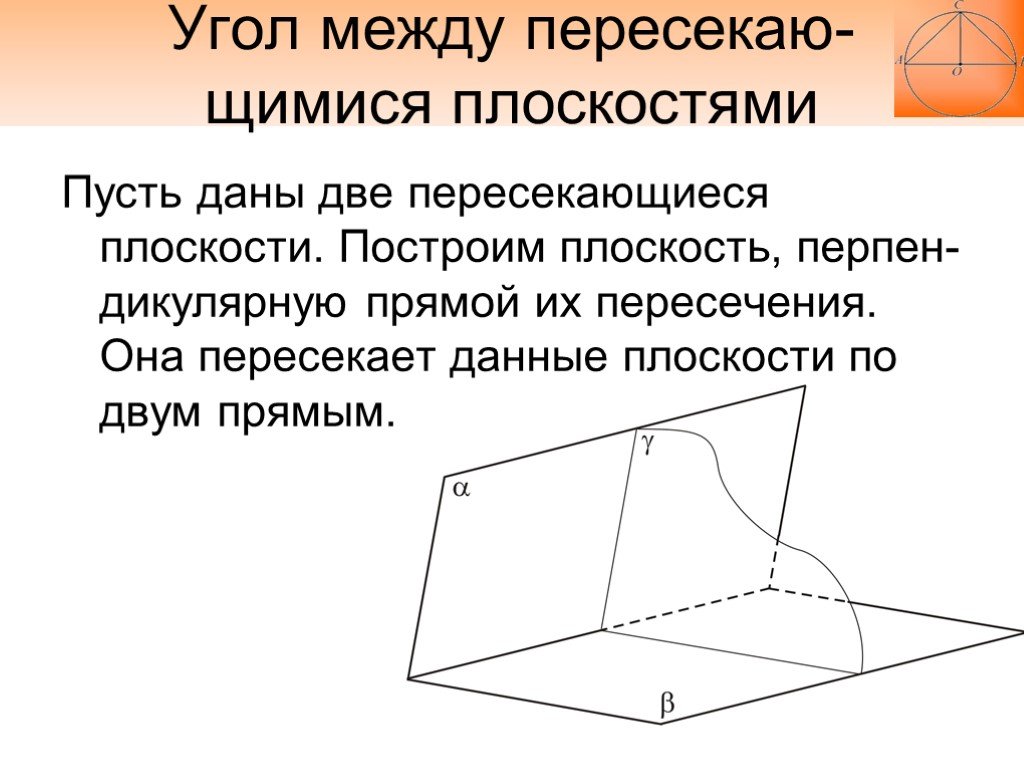
Пусть даны две пересекающиеся плоскости. Построим плоскость, перпен-дикулярную прямой их пересечения. Она пересекает данные плоскости по двум прямым.
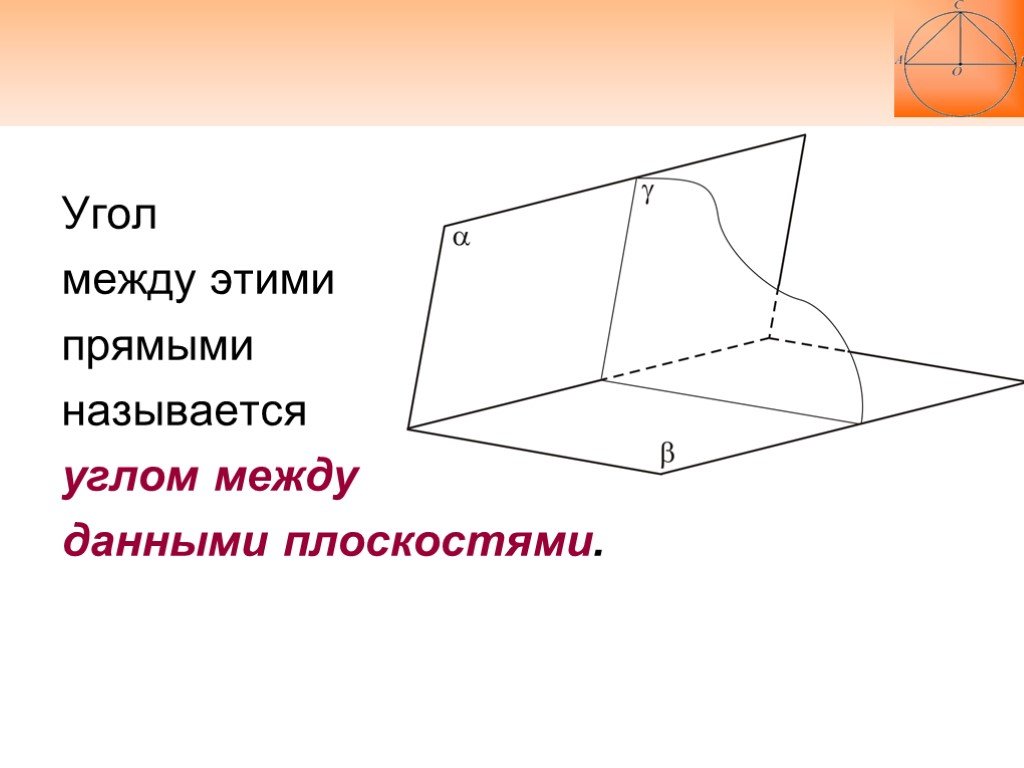
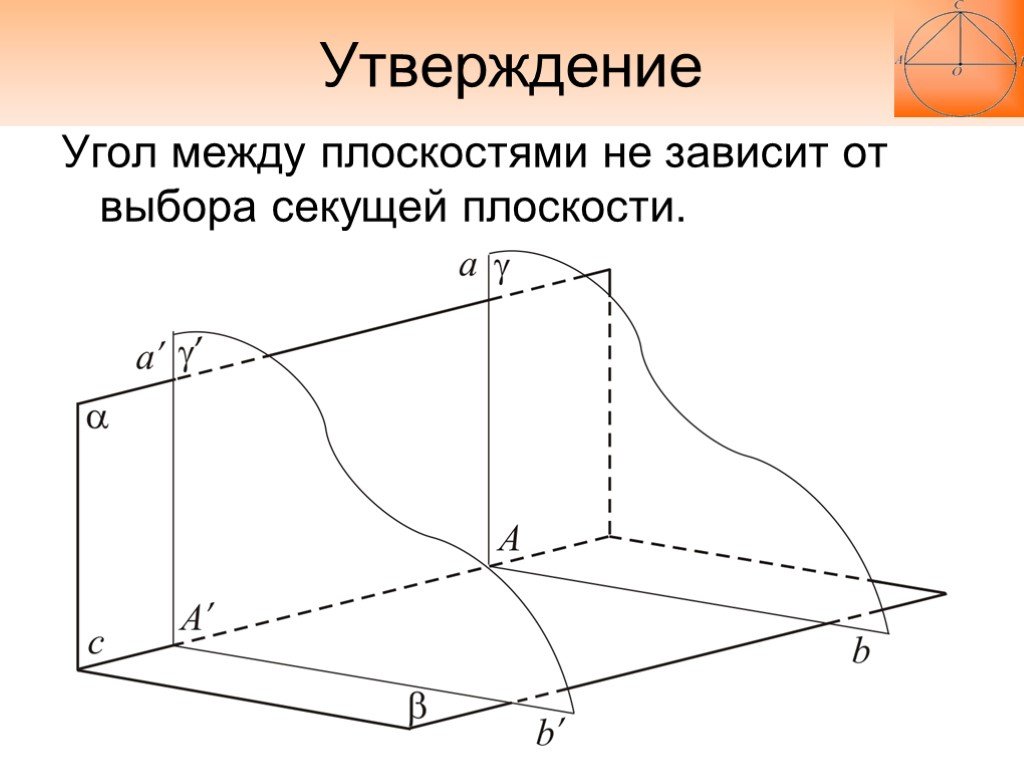
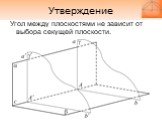
Слайд 29Угол между этими прямыми называется углом между данными плоскостями.
Слайд 30Угол между плоскостями не зависит от выбора секущей плоскости.
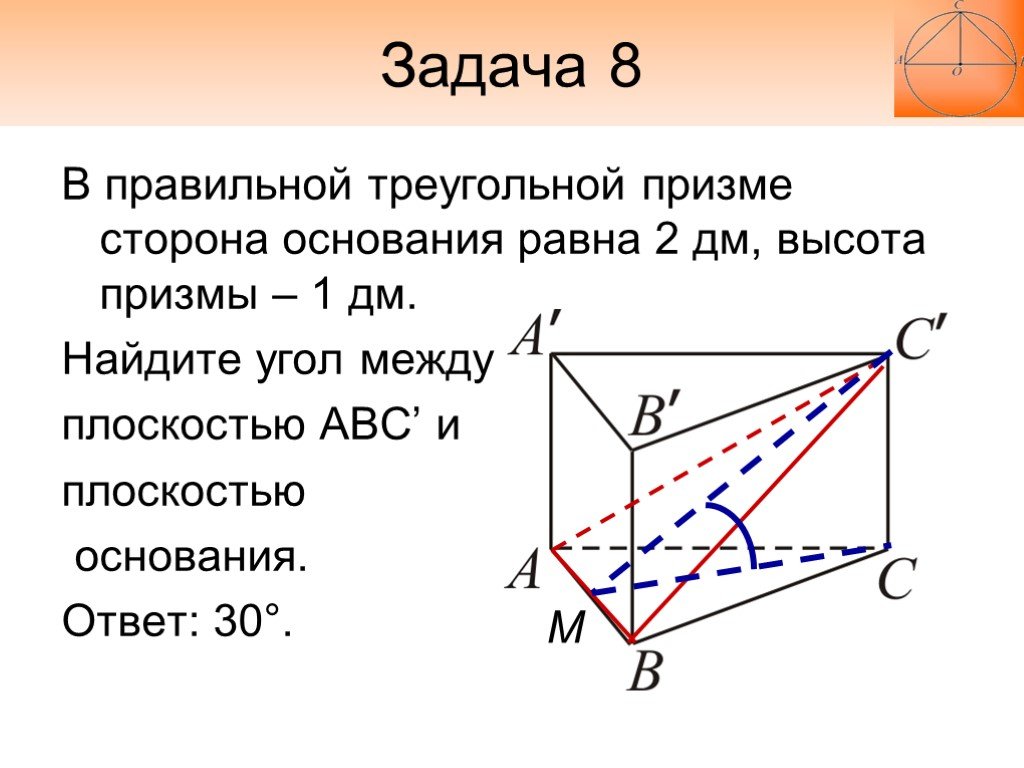
Слайд 31Задача 8
В правильной треугольной призме сторона основания равна 2 дм, высота призмы – 1 дм. Найдите угол между плоскостью ABC’ и плоскостью основания. Ответ: 30°.
М
Слайд 32Задачи для самостоятельного решения
В прямоугольном параллелепипеде ABCDA’B’C’D’ найдите угол между прямыми AD’ и C’D’. В правильной треугольной пирамиде SABC найдите угол между прямыми SC и CM, если сторона основания равна 3, а высота пирамиды .
Слайд 333. Дана правильная призма. Найдите угол между AC’ и BC’, если сторона тре-ка АВС равна 1см, а высота призмы равна 2 см. 4. В правильной четырехугольной пирамиде SABCD найдите угол между AS и BD. 5. В прямой треугольной призме ABCA’B’C’ стороны основания АВ =2, АС = АВ = 1. Боковое ребро равно 2 . Найдите угол между прямыми А’В и AC’.
Слайд 34Домашнее задание
Выучите определение угла между прямыми, между прямой и плоскостью и между плоскостями. Решите задачи для самостоятельного решения
Слайд 35