Презентация "Теоретические основы финансовых вычислений" – проект, доклад

Тема: Теоретические основы финансовых вычислений

"время – деньги"

ОБЩАЯ МЕТОДИКА ФИНАНСОВЫХ ВЫЧИСЛЕНИЙ

Важность учета фактора времени обусловлена принципом неравноценности денег, относящихся к различным моментам времени: равные по абсолютной величине денежные суммы "сегодня" и "завтра" оцениваются по разному, – сегодняшние деньги ценнее будущих.

Зависимость ценности денег от времени обусловлена влиянием фактора времени:

во-первых, деньги можно продуктивно использовать во времени как приносящий доход финансовый актив, т.е. деньги могут быть инвестированы и тем самым принести доход; во-вторых, инфляционные процессы ведут к обесцениванию денег во времени. Сегодня на рубль можно купить товара больше, чем завтра на этот же рубль, т.к. цены на товар повысятся; в-третьих, неопределенность будущего и связанный с этим риск повышает ценность имеющихся денег. Сегодня рубль в руке уже есть и его можно израсходовать на потребление, а будет ли он завтра в руке, – еще вопрос.

Финансовая математика – раздел количественного анализа финансовых операций, который решает следующие задачи:

исчисление будущей суммы денежных средств, находящихся во вкладах, займах или ценных бумагах путем начисления процентов; учет векселей; определение параметров сделки исходя из заданных условий; определение эквивалентности параметров сделки; анализ последствий изменения условий финансовой операции; исчисление обобщающих показателей финансовых потоков; определение параметров финансовой ренты; разработка планов выполнения финансовых операций; расчет показателей доходности финансовых операций.

Процентная ставка

Относительный показатель, характеризующий интенсивность начисления процентов за единицу времени, – процентная ставка. Методика расчета проста: отношение суммы процентных денег, выплачивающихся за определенный период времени, к величине ссуды. Этот показатель выражается либо в долях единицы, либо в процентах. Таким образом, процентная ставка показывает, сколько денежных единиц должен заплатить заемщик за пользование в течение определенного периода времени 100 единицами первоначальной суммы долга.

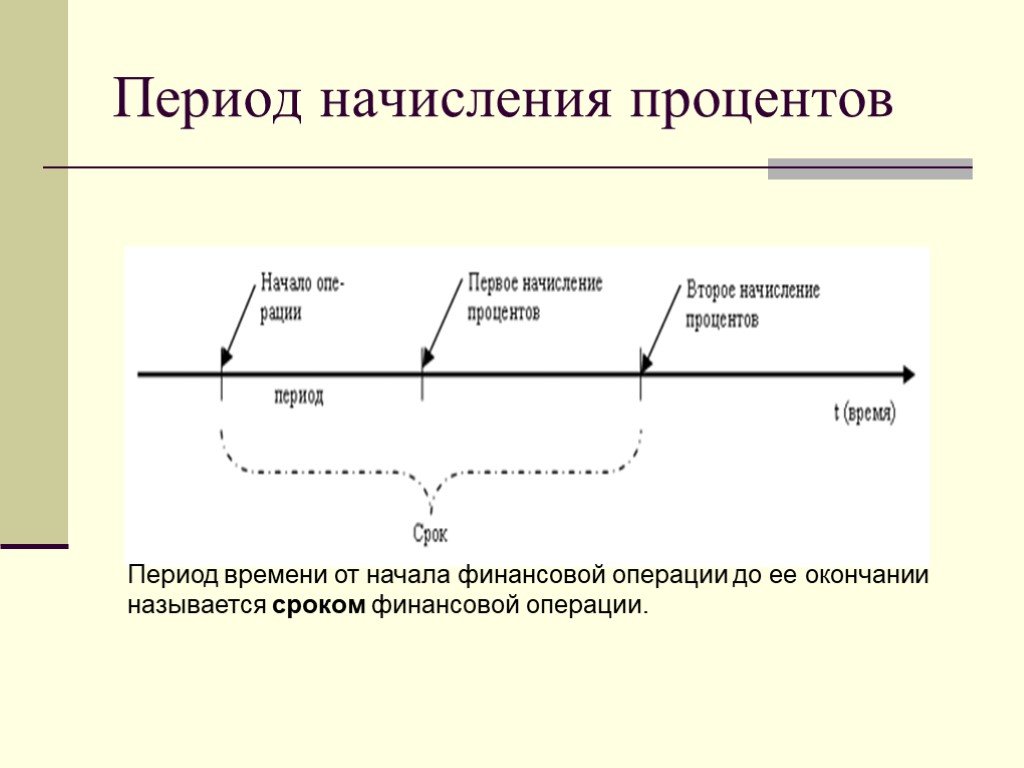
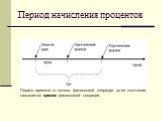
Период начисления процентов

"период начисления", – это отрезок времени между двумя следующими друг за другом процедурами взимания процентов. Обычные или декурсивные (postnumerando) проценты начисляются в конце периода. В качестве единицы периода времени в финансовых расчетах принят год, однако это не исключает использования периода менее года: полугодие, квартал, месяц, день, час.

Период времени от начала финансовой операции до ее окончании называется сроком финансовой операции.

Условные обозначения в финансовой математике

I – проценты за весь срок ссуды (interest); PV – первоначальная сумма долга или современная (текущая) стоимость (present value); i – ставка процентов за период (interest rate); FV – наращенная сумма или будущая стоимость (future value), т.е. первоначальная сумма долга с начисленными на нее процентами к концу срока ссуды; n – срок ссуды в годах.

Коэффициент наращения

Увеличение суммы долга в связи с присоединением к ней процентных денег называется наращением, а увеличенная сумма – наращенной суммой. Отсюда можно выделить еще один относительный показатель, который называется коэффициент наращения или множитель наращения, – это отношение наращенной суммы к первоначальной сумме долга. Коэффициент наращения показывает, во сколько раз наращенная сумма больше первоначальной суммы долга, т.е. по существу является базисным темпом роста.

Виды процентных ставок

Простая процентная ставка применяется к одной и той же первоначальной сумме долга на протяжении всего срока ссуды, т.е. исходная база (денежная сумма) всегда одна и та же. Сложная процентная ставка применяется к наращенной сумме долга, т.е. к сумме, увеличенной на величину начисленных за предыдущий период процентов, – таким образом, исходная база постоянно увеличивается. Фиксированная процентная ставка – ставка, зафиксированная в виде определенного числа в финансовых контрактах. Постоянная процентная ставка – неизменная на протяжении всего периода ссуды. Переменная процентная ставка – дискретно изменяющаяся во времени, но имеющая конкретную числовую характеристику. Плавающая процентная ставка – привязанная к определенной величине, изменяющейся во времени, включая надбавку к ней (маржу), которая определяется целым рядом условий (сроком операции и т.п.).

Основа процентной ставки

Основу процентной ставки составляет базовая ставка, которая является начальной величиной. Примером базовой ставки для зарубежных финансовых рынков могут служить лондонская межбанковская ставка ЛИБОР (LIBOR – London Interbank Offered Rate) или ставка ЛИБИД (LIBID – London Interbank Bid Rate), для России это ставка МИБОР (MIBOR – Moscow Interbank Offered Rate) или ставка МИБИД (MIBID – Moscow Interbank Bid Rate), а также ставка МИАКР (MIACR – Moscow Interbank Actual Credit Rate).

Финансовая операция наращения

Экономический смысл операции наращения состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции. Здесь идет движение денежного потока от настоящего к будущему.

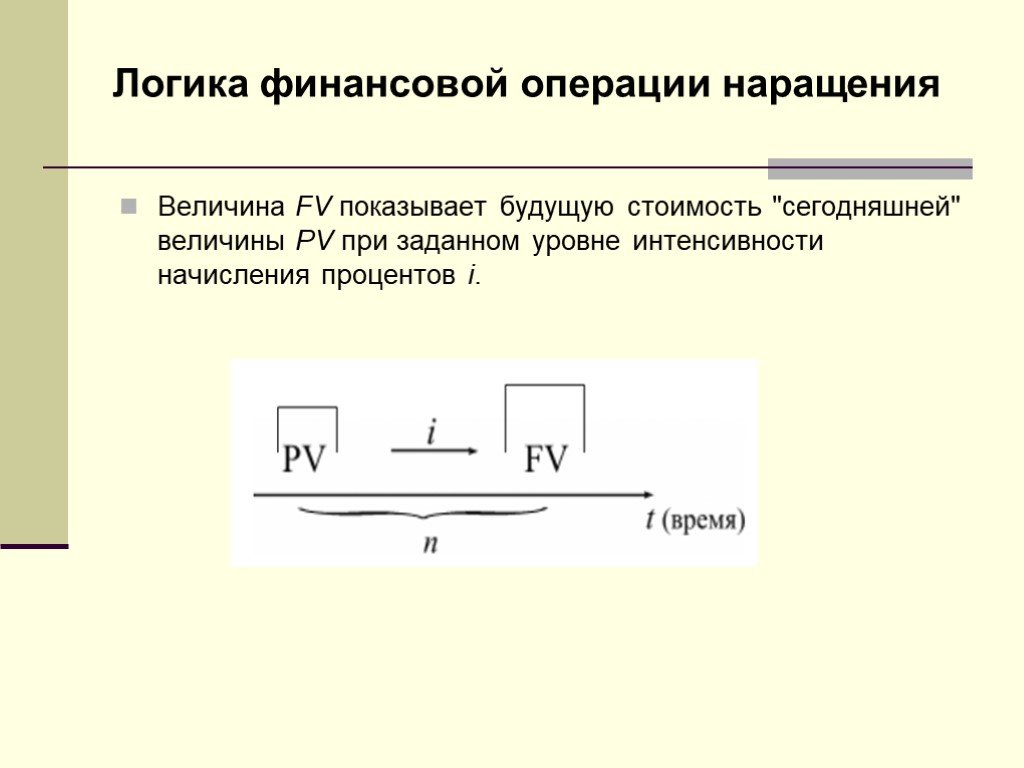
Логика финансовой операции наращения

Величина FV показывает будущую стоимость "сегодняшней" величины PV при заданном уровне интенсивности начисления процентов i.

Формула простого процента

Если учесть, что размер ожидаемого дохода зависит от трех факторов: от величины инвестированной суммы, от уровня процентной ставки и от срока финансовой операции, то наращенную сумму по схеме простых процентов можно будет определять следующим образом: FV = PV + I = PV + i • PV • n = PV (1 + i • n) = PV • kн, где kн – коэффициент (множитель) наращения простых процентов. Поскольку коэффициент наращения представляет собой значение функции от числа лет и уровня процентной ставки, то его значения легко табулируются.

Пример

Пример 1. Сумма в размере 2'000 рублей дана в долг на 2 года по схеме простого процента под 10% годовых. Определить проценты и сумму, подлежащую возврату. Решение: Наращенная сумма: FV = PV (1 + n • i ) = 2'000 (1 + 2 • 0'1) = 2'400 руб. или FV = PV • kн = 2'000 • 1,2 = 2'400 руб. Сумма начисленных процентов: I = PV • n • i = 2'000 • 2 • 0,1 = 400 руб. или I = FV - PV = 2'400 - 2'000 = 400 руб. Таким образом, через два года необходимо вернуть общую сумму в размере 2'400 рублей, из которой 2'000 рублей составляет долг, а 400 рублей – "цена долга".

Особенности базы расчета

Временную базу ( T ) можно представить по-разному: условно состоящую из 360 дней. В этом случае речь идет об обыкновенном (ordinary interest), или коммерческом проценте; взять действительное число дней в году (365 или 366 дней). В этом случае получают точный процент (exact interest). Число дней ссуды ( t ) также можно по-разному определять: условно, исходя из того, что продолжительность любого целого месяца составляет 30 дней, а оставшиеся дни от месяца считают точно, – в результате получают так называемое приближенное число дней ссуды; используя прямой счет или специальные таблицы порядковых номеров дней года, рассчитывают фактическое число дней между датами, – в этом случае получают точное число дней ссуды.

Если время финансовой операции выражено в днях

Расчет простых процентов может быть произведен одним из трех возможных способов: Обыкновенные проценты с приближенным числом дней ссуды, или, как часто называют, "германская практика расчета", когда продолжительность года условно принимается за 360 дней, а целого месяца – за 30 дней. Этот способ обычно используется в Германии, Дании, Швеции. Обыкновенные проценты с точным числом дней ссуды, или "французская практика расчета", когда продолжительность года условно принимается за 360 дней, а продолжительность ссуды рассчитывается точно по календарю. Этот способ имеет распространение во Франции, Бельгии, Испании, Швейцарии. Точные проценты с точным числом дней ссуды, или "английская практика расчета", когда продолжительность года и продолжительность ссуды берутся точно по календарю. Этот способ применяется в Португалии, Англии, США.

Примеры определения точного количество дней. Получается путем вычитания номера первого дня финансовой операции из номера последнего дня финансовой операции.

Пример 2. Сумма 2 млн руб. положена в банк 18 февраля не високосного года и востребована 25 декабря того же года. Ставка банка составляет 35% годовых. Определить сумму начисленных процентов при различной практике их начисления.

Германская практика начисления простых процентов:

Временная база принимается за 360 дней, T = 360. Количество дней ссуды: t = 11 (февраль) + 30 (март) + 30 (апрель) + 30 (май) + 30 (июнь) + + 30 (июль) + 30 (август) + 30 (сентябрь) + 30 (октябрь) + + 30 (ноябрь) + 25 (декабрь) - 1 = 305 дней Сумма начисленных процентов: I = P • t / T • i = 2'000'000 • 305/360 • 0,35 = 593'055,55 руб.

Французская практика начисления процентов:

Временная база принимается за 360 дней, T = 360. Количество дней ссуды: t = 11 (февраль) + 31 (март) + 30 (апрель) + 31 (май) + 30 (июнь) + + 31 (июль) + 31 (август) + 30 (сентябрь) + 31 (октябрь) + + 30 (ноябрь) + 25 (декабрь) - 1 = 310 дней Сумма начисленных процентов: I = P • t / T • i = 2'000'000 • 310/360 • 0,35 = 602'777,78 руб.

Английская практика начисления процентов:

Временная база принимается за 365 дней, T = 365. Количество дней ссуды берется точным, t = 310 дней. Сумма начисленных процентов: I = P • t / T • i = 2'000'000 • 310/365 • 0,35 = 594'520,55 руб.

Формула сложных процентов

Применение схемы сложных процентов целесообразно в тех случаях, когда: проценты не выплачиваются по мере их начисления, а присоединяются к первоначальной сумме долга. Присоединение начисленных процентов к сумме долга, которая служит базой для их начисления, называется капитализацией процентов; срок ссуды более года.

Методика определения формулы сложных процентов

Если процентные деньги не выплачиваются сразу по мере их начисления, а присоединяются к первоначальной сумме долга, то долг, таким образом, увеличивается на невыплаченную сумму процентов, и последующее начисление процентов происходит на увеличенную сумму долга: FV = PV + I = PV + PV • i = PV • (1 + i) – за один период начисления; FV = (PV + I) • (1 + i) = PV • (1 + i) • (1 + i) = PV • (1 + i)2 – за два периода начисления; отсюда, за n периодов начисления формула примет вид: FV = PV • (1 + i)n = PV • kн , где FV – наращенная сумма долга; PV – первоначальная сумма долга; i – ставка процентов в периоде начисления; n – количество периодов начисления; kн – коэффициент (множитель) наращения сложных процентов.

Сумма в размере 2'000 рублей дана в долг на 2 года по ставке процента равной 10% годовых. Определить проценты и сумму, подлежащую возврату. Решение: Наращенная сумма FV = PV • (1 + i)n = 2'000 • (1 + 0'1)2 = 2'420 рублей или FV = PV • kн = 2'000 • 1,21 = 2'420 рублей, где kн = 1,21 Сумма начисленных процентов I = FV - PV = 2'420 - 2'000 = 420 рублей. Таким образом, через два года необходимо вернуть общую сумму в размере 2'420 рублей, из которой 2'000 рублей составляет долг, а 420 рублей – "цена долга".

Эффективная ставка процентов

Период начисления по сложным процентам не всегда равен году, однако в условиях финансовой операции указывается не ставка за период, а годовая ставка с указанием периода начисления – номинальная ставка ( j ). Номинальная ставка (nominal rate) – годовая ставка процентов, исходя из которой определяется величина ставки процентов в каждом периоде начисления, при начислении сложных процентов несколько раз в год. Эта ставка во-первых, не отражает реальной эффективности сделки; во-вторых, не может быть использована для сопоставлений.

Учет в расчетах номинальной ставки

Если начисление процентов будет производиться m раз в год, а срок долга – n лет, то общее количество периодов начисления за весь срок финансовой операции составит N = n • m Отсюда формулу сложных процентов можно записать в следующем виде: FV = PV • (1 + j / m)N = P • (1 + j /m)mn , где j – номинальная годовая ставка процентов.

Изменим условия предыдущего примера, введя ежеквартальное начисление процентов. Решение: Количество периодов начисления: N = m • n = 4 • 2 = 8 Наращенная сумма составит: FV = PV • (1 + j / m)mn = 2'000 • (1 + 0,1 / 4 )8 = 2'436,81 руб. Сумма начисленных процентов: I = FV - PV = 2'436,81 - 2'000 = 436,81 руб. Таким образом, через два года на счете будет находиться сумма в размере 2'436,81 руб., из которой 2'000 руб. является первоначальной суммой, размещенной на счете, а 436,81 руб. – сумма начисленных процентов.

Эффективная ставка (effective rate)

Эффективная ставка (effective rate), измеряет тот реальный относительный доход, который получен в целом за год, с учетом внутригодовой капитализации. Эффективная ставка показывает, какая годовая ставка сложных процентов дает тот же финансовый результат, что и m-разовое наращение в год по ставке j / m: (1 + i)n = (1 + j / m)m • n, следовательно, i = (1 + j / m)m - 1. Из формулы следует, что эффективная ставка зависит от количества внутригодовых начислений.

Сущность дисконтирования

В финансовой практике часто приходится решать задачи, обратные определению наращенной суммы: по уже известной наращенной сумме (FV) следует определить неизвестную первоначальную сумму долга (PV). Такие ситуации возникают при разработке условий финансовой сделки, или когда проценты с наращенной суммы удерживаются непосредственно при выдаче ссуды. Процесс начисления и удержания процентов вперед, до наступления срока погашения долга, называют учетом, а сами проценты в виде разности наращенной и первоначальной сумм долга дисконтом (discount): D = FV - PV

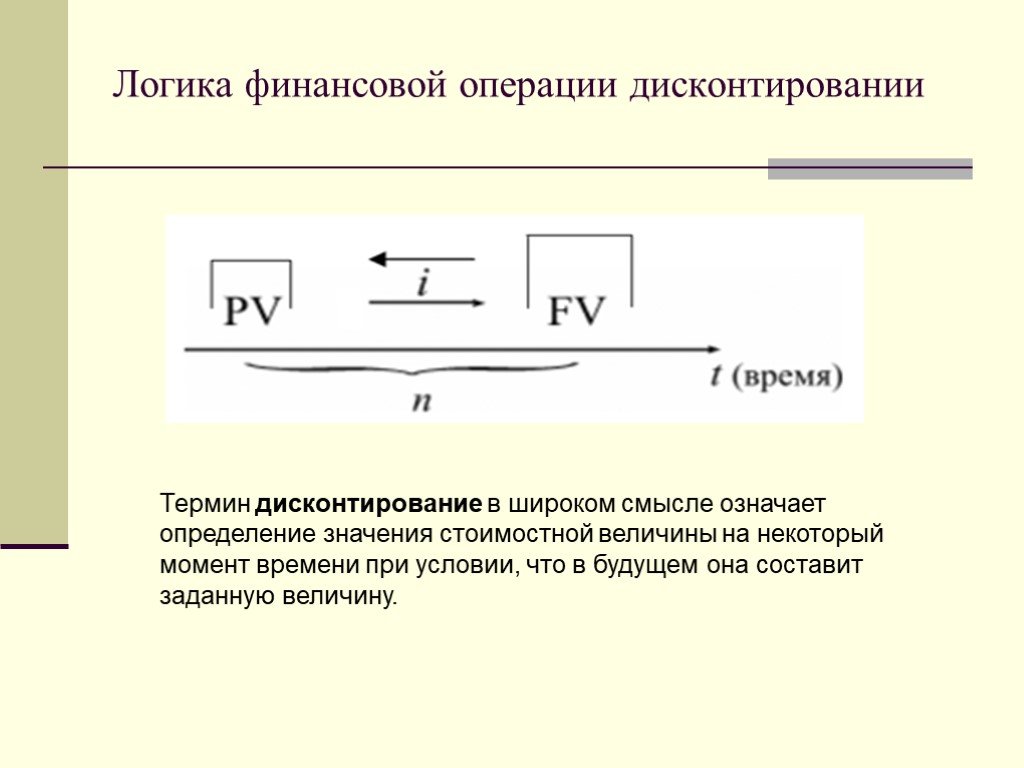
Логика финансовой операции дисконтировании

Термин дисконтирование в широком смысле означает определение значения стоимостной величины на некоторый момент времени при условии, что в будущем она составит заданную величину.

Не редко такой расчет называют приведением стоимостного показателя к заданному моменту времени, а величину PV называют приведенной(современной или текущей) величиной FV. Таким образом, дисконтирование – приведение будущих денег к текущему моменту времени, и при этом не имеет значения, имела ли место в действительности данная финансовая операция или нет, а также независимо от того, можно ли считать дисконтируемую сумму буквально наращенной. Именно дисконтирование позволяет учитывать в стоимостных расчетах фактор времени, поскольку дает сегодняшнюю оценку суммы, которая будет получена в будущем. Привести стоимость денег можно к любому моменту времени, а не обязательно к началу финансовой операции.

Методика дисконтирования

Исходя из методики начисления процентов, применяют два вида дисконтирования: математическое дисконтирование по процентной ставке; банковский учет по учетной ставке. Дисконтирование – определение первоначальной суммы долга, которая при начислении процентов по заданной величине процентной ставки (i ) позволит к концу срока получить указанную наращенную сумму.

Дисконтирование для простых процентов

для простых процентов PV = FV : (1 + n • i ) = FV • 1 / (1 + n • i ) = = FV • (1 + n • i ) -1 = FV • kд, где kд – дисконтный множитель (коэффициент приведения) для простых процентов. Пример: Через 150 дней с момента подписания контракта необходимо уплатить 310 тыс. руб., исходя из 8% годовых и временной базы 360 дней. Определить первоначальную сумму долга. Решение: Поскольку срок ссуды менее года, то используем формулу простых процентов: PV = FV • 1 / (1 + t / T • i ) = 310'000 • 1 / (1 + 150 / 360 • 0,08) = 300'000 руб. PV = FV • kд = 310'000 • 0,9677419 = 300'000 руб. Таким образом, первоначальная сумма долга составила 300 тыс. руб., а проценты за 150 дней – 10 тыс. руб.

Дисконтирование для сложных процентов

PV = FV • (1 + i) -n = FV • kд, где kд – дисконтный множитель для сложных процентов. Если начисление процентов производится m раз в год, то формула примет вид: PV = FV • (1 + j / m) -m • n . Пример. Через два года фирме потребуется деньги в размере 30 млн руб., какую сумму необходимо сегодня поместить в банк, начисляющий 25% годовых, чтобы через 2 года получить требуемую сумму? Решение: Поскольку срок финансовой операции составляет более года, что используем формулу приведения для сложных процентов: PV = FV • 1 / (1 + i) n = 30'000'000 • 1 / (1 + 0,25)2 = 19'200'000 руб. или PV = FV • kд = 30'000'000 • 0,6400000 = 19'200'000 руб. Таким образом, фирме следует разместить на счете 19'200'000 руб. под 25% годовых, чтобы через два года получить желаемые 30'000'000 руб.

Сущность потока платежей - аннуитета

Поток платежей, все члены которого имеют одинаковое направление (знак), а временные интервалы между последовательными платежами постоянны, называется финансовой рентой или аннуитетом. При рассмотрении финансовой ренты используются основные категории: член ренты (PMT) – величина каждого отдельного платежа; срок ренты (n) – время от начала финансовой ренты до конца последнего ее периода; процентная ставка (i) – ставка, используемая при наращении платежей, из которых состоит рента.

Наращенная величина аннуитета

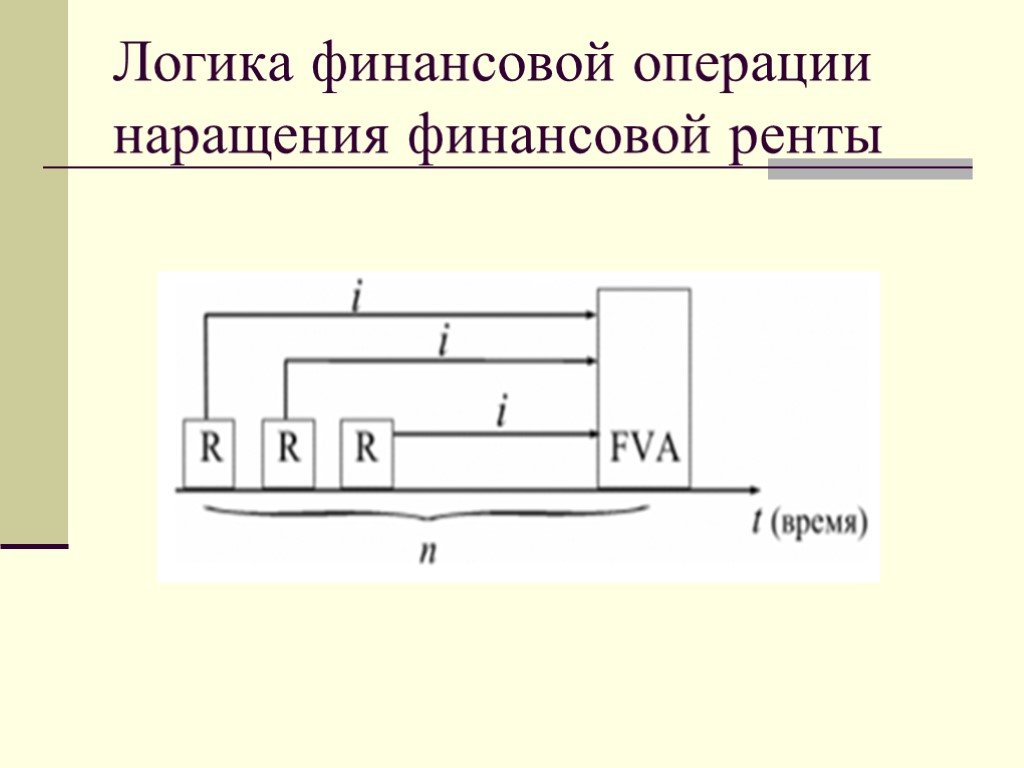
Наращенная сумма – сумма всех платежей с начисленными на них процентами к концу срока ренты. Это может быть обобщенная сумма задолженности, итоговый объем инвестиций и т.п. Наращенные отдельные платежи представляют собой члены геометрической прогрессии с первым членом равным R и множителем равным (1 +i).

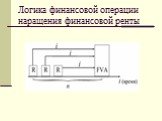
Логика финансовой операции наращения финансовой ренты

Годовая постоянная обычная рента

где FVA – наращенная сумма ренты; R (PMT) – размер члена ренты, т.е. размер очередного платежа; i – годовая процентная ставка, по которой на платежи начисляются сложные проценты; n – срок ренты в годах, s n;i – коэффициент наращения ренты

На счет в банке в течении пяти лет в конце каждого года будут вноситься суммы в размере 500 руб., на которые будут начисляться проценты по ставке 30%. Определить сумму процентов, которую банк выплатит владельцу счета. Решение: Период ренты равен одному году- это годовая рента; Взносы будут в конце периода ренты, постнумерандо-это обычная рента; Число членов ренты пять Сумма всех взносов с начисленными процентами будет равна: Можно определить наращенную сумму постоянной ренты, воспользовавшись финансовыми таблицами, содержащими коэффициенты наращения ренты: FVA = R • s5 ; 30 = 500 • 9,0431 = 4'521,55 руб. Сумма взносов в течение 5 лет составит: P = n • R = 5 • 500 = 2'500 руб. Следовательно, сумма начисленных процентов будет равна: I = FVA - P = 4'521,55 - 2'500 = 2'021,55 руб. Таким образом, доход владельца счета за 5 лет составит 2'021,55 руб.

Современная (текущая) величина аннуитета

1. Современная (текущая) величина потока платежей (капитализированная или приведенная величина) – это сумма платежей, дисконтированных на момент начала ренты по ставке начисляемых сложных процентов. 2. Это важнейшая характеристика финансового анализа, т.к. является основой для измерения эффективности различных финансово-кредитных операций, сравнения условий контрактов и т.п. 3. Данная характеристика показывает, какую сумму следовало бы иметь первоначально, чтобы, разбив ее на равные взносы, на которые начислялись бы установленные проценты в течение всего срока, можно было бы получить указанную наращенную сумму.

Логика финансовой операции определения современной величины потока платежей

Определить по данным примера современную величину ренты. Решение: Современная величина ренты составит: Таким образом, все производимые в будущем платежи оцениваются в настоящий момент в размере 1'217,78 руб.

Определение параметров аннуитета

Последовательные платежи в виде постоянной обычной годовой ренты определяются основными параметрами: R (PMT)– размер платежа; n – срок ренты в годах; i – годовая ставка процентов. При разработке условий финансовой операции могут возникать ситуации, когда заданной величиной является одна из двух обобщающих характеристик и неполный набор параметров ренты. В таких случаях находят недостающий параметр.

При определении члена ренты возможны два варианта

1 вариант - наращенная сумма. Если сумма долга определена на какой-либо момент в будущем (FVA), тогда величину последующих взносов в течение n лет при начислении на них процентов по ставке i можно определить по формуле:

Для покупки автомобиля через 5 лет потребуется 50 тыс. руб. Определите размер ежегодных взносов, вносимых в конце каждого года в банк, который начисляет проценты по ставке 40%. Решение: В данном случае известна наращенная величина постоянной финансовой ренты, поэтому размер ежегодных взносов будет равен: Таким образом, чтобы накопить на счете необходимую сумму для покупки автомобиля следует в конце каждого года в течении пяти лет откладывать 4'568 руб.

2 вариант - современная величина финансовой ренты, тогда, исходя из ставки процента и срока ренты, разовый платеж находится по формуле:

Сумма 10 тыс. рублей предоставлена в долг на 5 лет под 8% годовых. Определить ежегодную сумму погашения долга. Решение: Известна современная величина долга, отсюда: Таким образом, ежегодно необходимо будет возвращать сумму 2'504,56 руб.