Презентация "Параллелепипед" по математике – проект, доклад
Презентацию на тему "Параллелепипед" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 13 слайд(ов).
Слайды презентации
Список похожих презентаций
Тетраэдр и Параллелепипед
Содержание:. 1)Титульный лист 2)Определение тетраэдра и его свойства 3)Построение тетраэдра 4)Формула объема тетраэдра 5)Определение параллелепипеда ...Тетраэдр. Параллелепипед
Тетраэдр. Рассмотрим произвольный треугольник АВС и точку D, не лежащую в плоскости этого треугольника. Содержание. Соединив точку D отрезками с вершинами ...Параллелепипед и его объем
Для начала введем одно важное понятие: Призма, все грани которой являются параллелограммами, называется параллелепипедом. Окружающие нас предметы ...Перпендикулярность плоскостей Параллелепипед
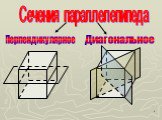
Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 900. Примером взаимно перпендикулярных ...Параллелепипед
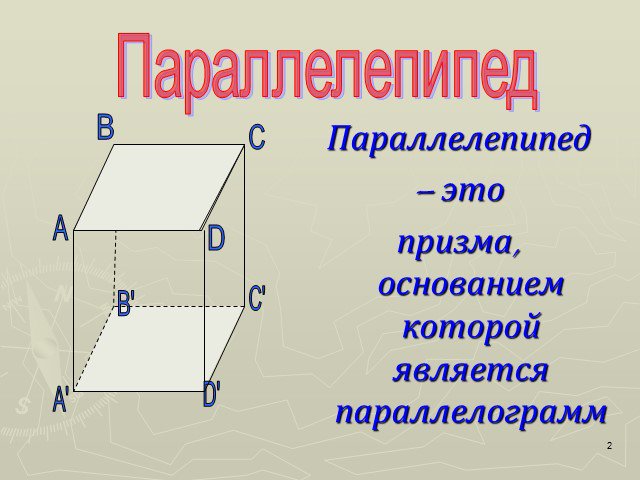
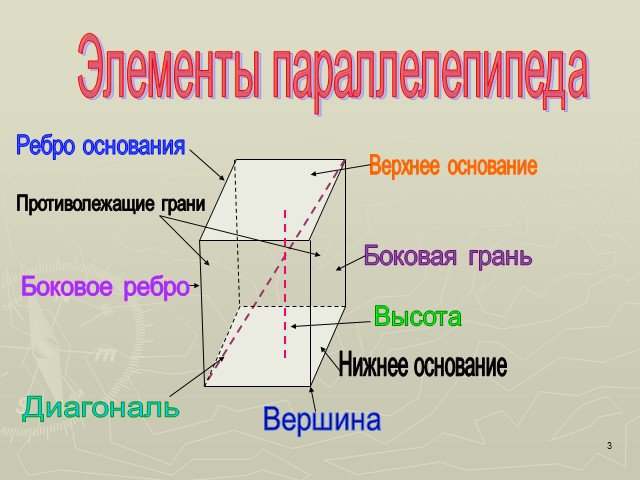
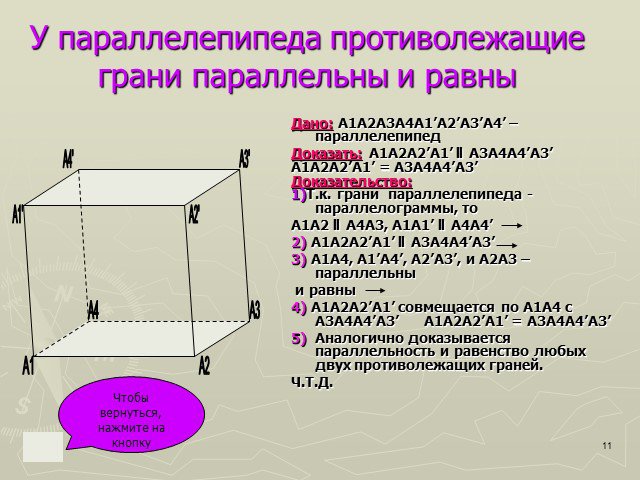
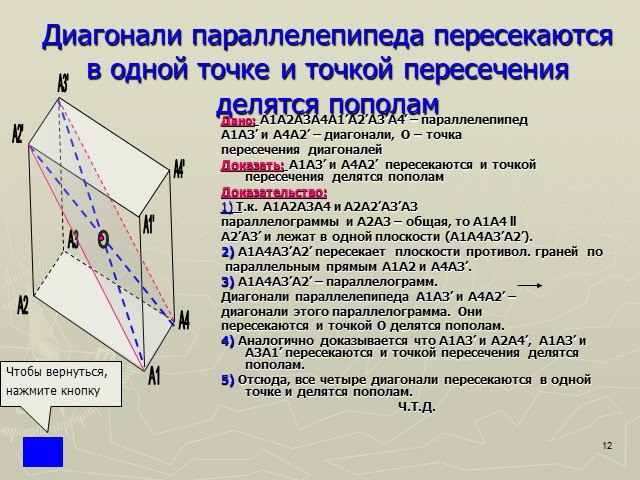
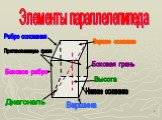
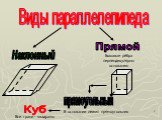
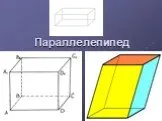
Параллелепипед – шестигранник, противоположные грани которого попарно параллельны. Параллелепипед имеет: 8 вершин 12 рёбер 6 граней. Определение Вершина ...Параллелепипед
Текст надписи. Параллелепи́пед (от греч. παράλλος — параллельный и греч. επιπεδον — плоскость) — призма, основанием которой служит параллелограмм, ...Параллелепипед
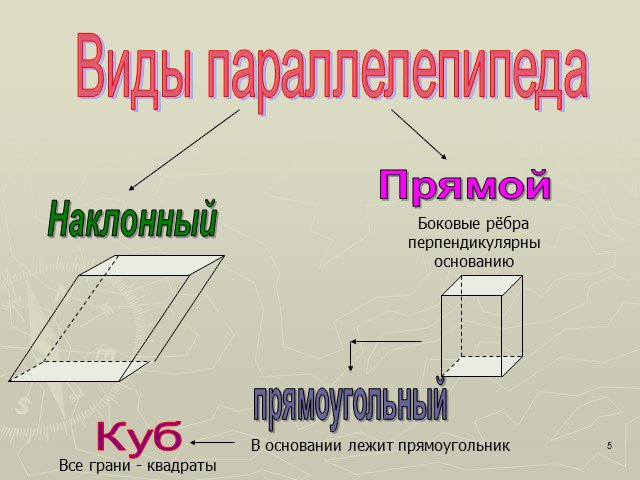
Параллелепипед – четырёхугольная призма, основаниями которой являются параллелограммы. Прямой параллелепипед, т.е. его боковые рёбра перпендикуляр-ны ...Параллелепипед
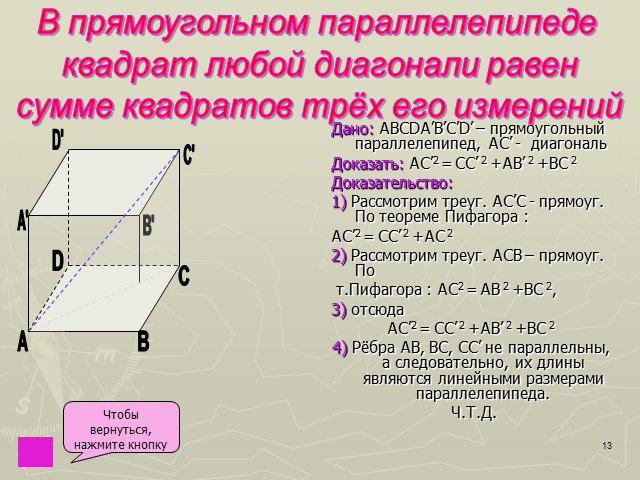
Прямоугольный параллелепипед. Спичечный коробок, деревянный брусок, кирпич дают представление о прямоугольном параллелепипеде. Поверхность прямоугольного ...Параллелепипед
Параллелепи́пед. Параллелепи́пед (от греч. παράλλος — параллельный и греч. επιπεδον — плоскость) — призма, основанием которой служит параллелограмм, ...Параллелепипед
Параллелепипед- четырехугольная призма, основаниями которой являются параллелограммы. Все шесть граней параллелепипеда- параллелограммы. Ребра (12) ...Параллелепипед
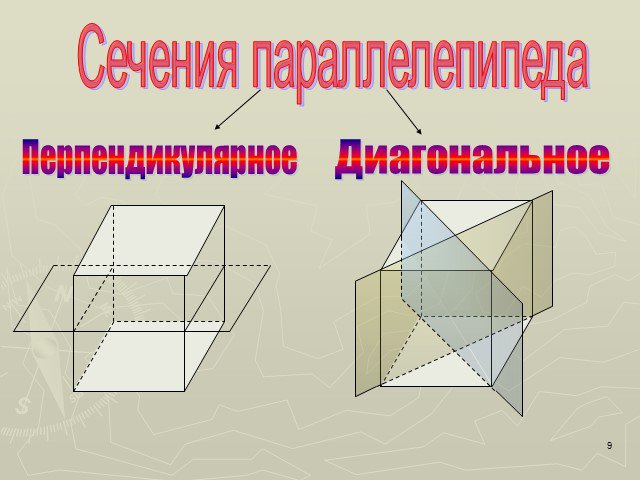
Прямоугольный параллелепипед. Параллелепипед. A B C D. 1. ABCD, A1B1C1D1, AA1D1D, … 2. A, AB, AC, AA1, B, BC, BB1, …. A1 B1 C1 D1. Смежные грани. ...Конспекты
Параллелепипед и его свойства
Конспект урока по геометрии для учащихся 10 класса средней общеобразовательной школы. Тема урока:. «. Параллелепипед и его свойства». Цель ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Математика
Автор презентации:ученица: Рябова Мария, руководитель: учитель математики Орлова Н.В.
Содержит:13 слайд(ов)
Поделись с друзьями:
Скачать презентацию