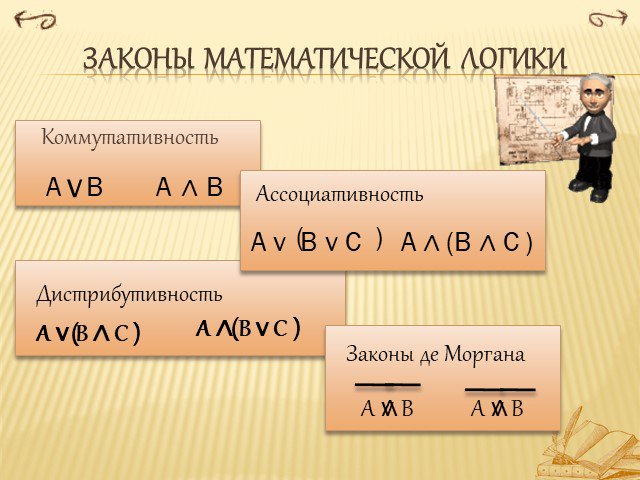
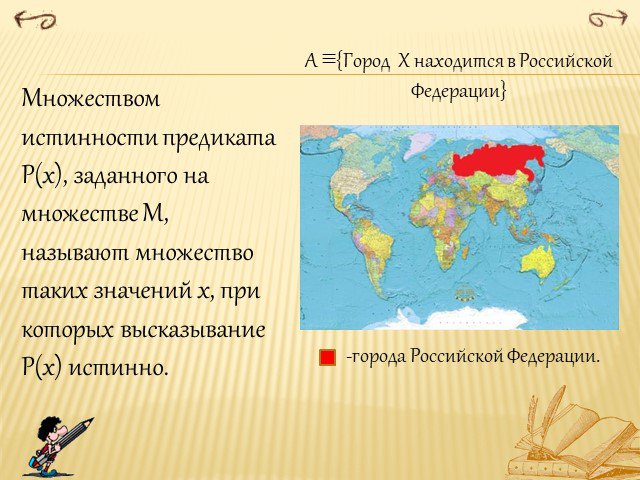
Презентация "Математическая логика" по математике – проект, доклад
Презентацию на тему "Математическая логика" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 28 слайд(ов).
Слайды презентации
Список похожих презентаций
Математическая семья
I тур. ПРЕДСТАВЛЕНИЕ СЕМЕЙ: название команды эмблема девиз. II тур. РАЗМИНКА Какая дробь называется правильной? 32 = ? Формула площади прямоугольника? ...Математическая сказка
Жил да был царь. У царя было три сына: Федор, Егор и Иван. Богатств у царя было – не счесть. Да стал он болеть. Вот и посылает он сыновей за живой ...Жизнь и логика
Цели и задачи. Формирование навыков самостоятельной работы с информационными ресурсами Формирование навыков коллективной работы Развитие творческих ...Математическая регата
ПРАВИЛА ПРОВЕДЕНИЯ. 1. Участвуют несколько команд. В составе каждой команды - 4 человека. 2. Соревнование проводится в 3 - 4 тура. Каждый тур представляет ...Математическая статистика и теория вероятностей
Вероятностей теория, раздел математики, в котором по данным вероятностям одних случайных событий находят вероятности других событий, связанных каким ...Математическая эстафета
Вставить пропущенное слово в пословицу. 1. Все за одного, … за всех. 2. … раз примерь, … раз отрежь. 3. Не имей … рублей, а имей … друзей. 4. Ум хорошо, ...Математическая викторина
Команды. 1 команда Умники 2 команда Смекалистые 3 команда Почемучки. Наши капитаны. Афанасьев Егор Захарова Екатерина Шиловский Федор. 1 тур - конкурс ...Математическая статистика
В математической статистике разрабатываются теории и методы обработки информации о массовых явлениях и их назначении Для этого проводится статистическое ...Математическая викторина
. . . . . . . . . Информационные источники. Девочка со счётами http://korkinodetsad.ru/i/img/58.jpg Мальчик https://fs00.infourok.ru/images/doc/264/269447/hello_html_m55378ed.png ...Математическая викторина
. . . . . . . . . Информационные источники. Девочка со счётами http://korkinodetsad.ru/i/img/58.jpg Мальчик https://fs00.infourok.ru/images/doc/264/269447/hello_html_m55378ed.png ...Математическая викторина
Цели проведения викторины:. Развивать логическое мышление, сообразительность учащихся; Прививать интерес к математике; Развивать преемственность между ...Математическая «Своя игра»
1-ый раунд разминка. Разминка: 1. Шарада Баллы: 10 15 2. Отгадай-ка! Предлог и малое число За ними букву скажем. А в целом - ты найдёшь его Почти ...Кто хочет стать отличником? Математическая игра
В семье пять сыновей. Каждый имеет одну сестру. Сколько всего детей в семье? А Пять B Десять C Девять D Шесть Вопрос 1. Если два петуха закричат изо ...Математическая сказка
План - карта страны. Лесная школа Морская бухта д. Репкино г. Буратинск с. Незнайкино. 1 4 6 5 2 7 8 9 10. Станция "Лесная школа". 5 + 2 6 + 3 2 + ...Математическая викторина
I тур. Математическая викторина. II тур. III тур. Вопрос: Какая фигура – лишняя? Ответ : желтый параллелограмм. Математика и природа (200 баллов). ...Математическая сказка "История одного числа"
Содержание Часть1. «Слезы…слезы…слезы.. Часть2.Волшебная ночь Часть3. Чудесное превращение. Часть 1. Ой-ё-ей !-послышался горький плач. Это плакало ...Математическая викторина "Кто хочет стать миллионером?" Обобщающее повторение по теме «Стереометрия»
Вопросы для выбора игроков. №1. Наибольшее отрицательное целое число? -1 1 комплект. №2.Чему равно число ? 2 комплект. №3. Третья буква греческого ...Математическая статистика в жизни нашего класса
Эпиграф. Без знания математики нельзя понять ни основ современной техники, ни того, как учёные изучают природные и социальные явления. Колмогоров ...Математическая викторина "О математике с улыбкой"
Н.Н.Коломина. Известно ли вам, что математика – очень веселая наука? Ведь ее можно увидеть во всем, что нас окружает. Математическая викторина «О ...Математическая чехарда
1. За чем вода в стакане? 2. Будильник в средневековье. 3. По чему лампа вкручивается? 4. Ледяная корка на дороге. 5. Бумажный летательный аппарат. ...Конспекты
Язык и логика
Разработка урока. Очеретова Тамара Ивановна. Интегрированный урок по математике, информатике и русскому языку. «Язык и логика». ...Язык и логика
Конспект занятия по теме: «Язык и логика». . Цели урока:. . Закрепление изученных понятий математической логики: высказывание, тема, рема, истинное ...Математическая шкатулка
ТОГБОУ «Инжавинская специальная (коррекционная) общеобразовательная школа-интернат». Программа математического кружка. «Математическая ...Что такое логика
Республика Коми. МОУ «Чимская основная общеобразовательная школа». Методическая разработка. внеклассного мероприятия. . по математике. ...Математическая спартакиада
Автор:. Дорофеева Лилия Ильинична. Полное название образовательного учреждения:. . Муниципальное бюджетное образовательное учреждение «Средняя ...Математическая статистика в жизни класса
. Тема урока: «Математическая статистика в жизни класса». Цели. :. Образовательные:. . Обобщение и систематизация знаний по обработке информации, ...Математическая связь между суммой и слагаемыми
Математика в 1-м классе. Урок-путешествие "Остров сокровищ". «Математическая связь между суммой и слагаемыми». Цели:. познакомить со взаимосвязью ...Математическая сказка
. Интегрированный урок «Математическая сказка». (математика и литература). в 7 классе по теме «Решение уравнений». Боброва Наталья Александровна. ...Математическая рыбалка
Муниципальное дошкольное образовательное учреждение. . «Детский сад компенсирующего вида» № 26 г. Вологды. Конспект урока математики ...Математическая поляна
Муниципальное бюджетное общеобразовательное учреждение. гимназия №1 города Лебедяни Липецкой области. Конспект урока. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Математика
Автор презентации:Уученицы Баженова На., Луценко К., Масленникова Л., Саяпина Ю.
Содержит:28 слайд(ов)
Поделись с друзьями:
Скачать презентацию