Презентация "Осевая симметрия" по математике – проект, доклад
Презентацию на тему "Осевая симметрия" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 23 слайд(ов).
Слайды презентации
Список похожих презентаций
Движения в пространстве Центральная симметрия Осевая симметрия Зеркальная симметрия Параллельный перенос
Форма урока: Урок – семинар, решение проблемного вопроса. Цели урока: Актуализировать личностное осмысление учащимися учебного материала «Движения ...Осевая симметрия
ОСЕВАЯ Симметрия. — тип симметрии, имеющий несколько отличающихся определений: Отражательная симметрия. В евклидовой геометрии осевая симметрия — ...Осевая симметрия
Симметрия. В общем смысле симметрия – это свойство геометрической фигуры, характеризующее некоторую правильность формы фигуры, неизменность ее при ...Осевая симметрия
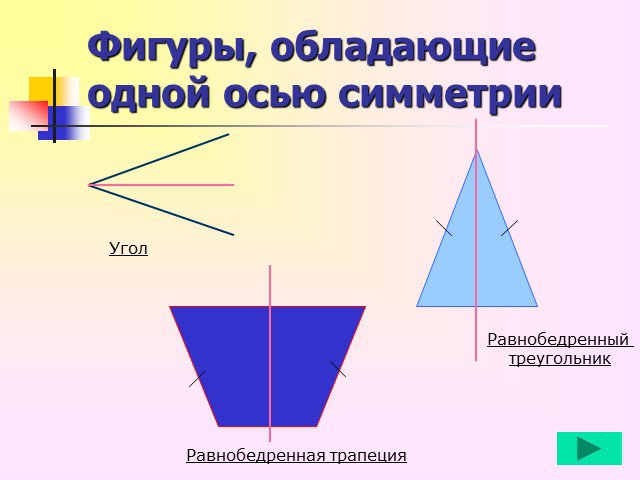
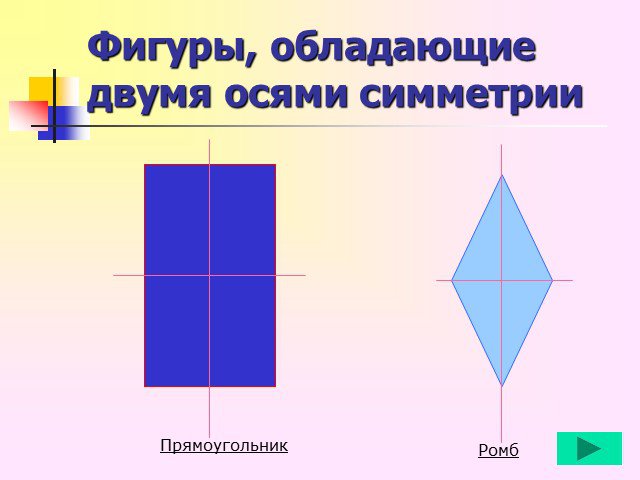
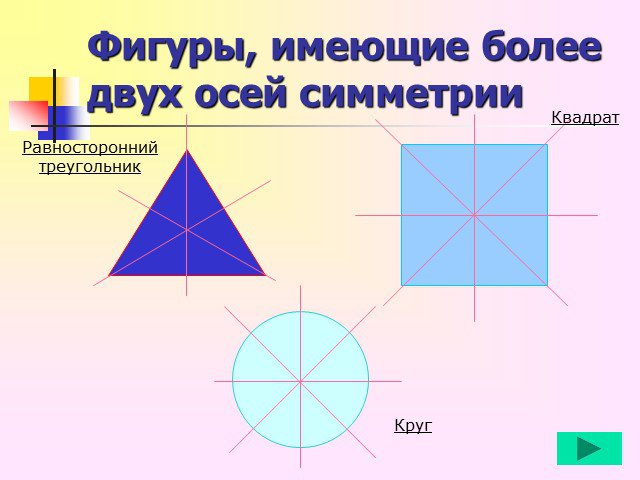
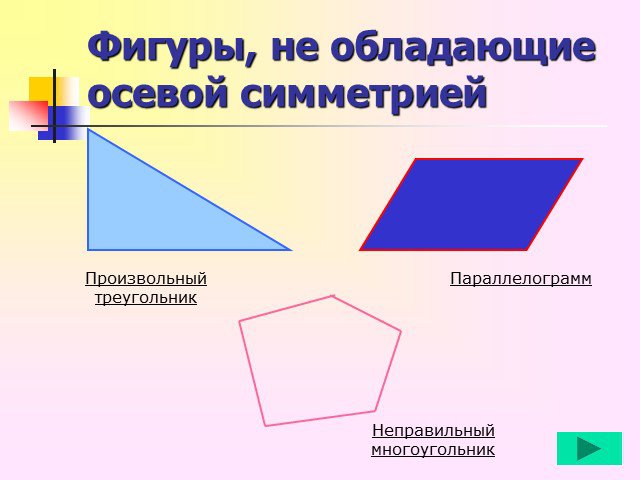
К первой группе относиться центрально-симметричные фигуры. Во второй группе. К третьей группе относится фигуры, которые состоят как бы из двух половинок,одна ...Осевая симметрия
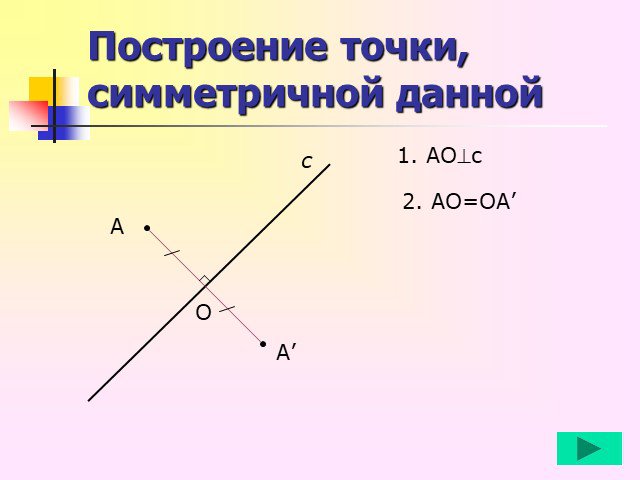
Точки А и В называют симметричными относительно прямой l, если l является серединным перпендикуляром отрезка АВ. A B O l ОСЬ СИММЕТРИИ. G F. Фигура ...Осевая симметрия
Цели урока. Ввести понятие точек и фигур, симметричных относительно прямой Научить строить симметричные точки и распознавать фигуры, обладающие осевой ...Осевая симметрия
. . . . . Центральная симметрия. . . . . . Да, в математике, как ни в какой другой науке находит выражение важнейший критерий научной красоты – единство ...Осевая симметрия
Содержание:. Определение симметрии, виды симметрии. Осевая симметрия. Теорема. Симметрия – (от греч.) соразмерность, пропорциональность, одинаковость ...Осевая симметрия
Осевая симметрия представляет собой отображение плоскости на себя. a M1 M P. Пусть а – ось симметрии. Возьмём М, не лежащую на прямой а. Построим ...Осевая симметрия
«… быть прекрасным значит быть симметричным и соразмерным» Платон. Симметрия – это идея, с помощью которой человек веками пытался объяснить и создать ...Осевая симметрия Занятие 26
Разминка №1. Четырёх ребят спросили, какого цвета автомобиль стоял во дворе и какой номер у него? Выяснилось, что каждый один раз сказал правду, а ...Осевая симметрия
Разминка №1. 6 мальчиков и 4 девочки за перемену могут съесть 36 булочек. Сколько булочек при таком аппетите могут съесть 9 мальчиков и 6 девочек? ...Осевая симметрия
Определение. Так же осевая симметрия используется в архитектуре. В живописи. Словом, симметрия встречается повсеместно в нашей жизни . ...Осевая симметрия
Симметрия относительно прямой — это осевая симметрия. Симметрия относительно прямой (оси симметрии) предполагает, что по перпендикуляру, проведенному ...Осевая симметрия
Цель урока: ввести понятие «симметрия», конкретизировать понятие на примере осевой симметрии. Содержание: 1) определение симметрии, виды симметрии ...Осевая и центральная симметрия
Осевая симметрия. А В а О С. Две точки А и В называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АВ и ...Осевая и центральная симметрия
Цель:. Сформировать общее представление о цетральной и осевой симметрии. Задачи:. 1. Дать определение центральной и осевой симметрии. 2. Рассмотреть ...Виды симметрии. Центральная и осевая симметрия
ОСЕВАЯ(ЗЕРКАЛЬНАЯ) СИММЕТРИЯ. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ. Что такое симметрия? Какие точки называются симметричными? Симметрия – это соразмерность, одинаковость ...Симметрия. Осевая и центральная симметрии
Слово «симметрия» греческого происхождения («сим» - с, «метрон» - мера) и буквально означает «соразмерность». Симметрия является той идеей, с помощью ...Центральная и осевая симметрия
Движение пространства – это отображение пространства на себя, сохраняющее расстояния между точками (любые две точки А и В переходят (отображаются) ...Конспекты
Осевая симметрия
Кировское областное государственное общеобразовательное. бюджетное учреждение. средняя общеобразовательная школа. с углубленным изучением отдельных ...Центральная и осевая симметрия
Тема: “Центральная и осевая симметрия”. Цели:. научить строить симметричные точки и распознавать фигуры, обладающие симметрией;. . подготовка ...Осевая и центральная симметрия
Тема урока:. Осевая и центральная симметрия. Учитель: Филькина Елена Николаевна. . Класс: 9. . Цели:. Обучающая:. расширить понятия об ...Осевая и центральная симметрии
МБОУ ООШ с. Старосеменкино муниципального района Белебеевский район РБ. Учитель математики Федорова Роза Климовна. Тема урока: «Осевая и центральная ...Осевая и центральная симметрии
Конспект урока геометрии в 8 классе по теме. . «Осевая и центральная симметрии». Цели. Проверить усвоение изученных свойств четырёхугольников. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:25 апреля 2015
Категория:Математика
Содержит:23 слайд(ов)
Поделись с друзьями:
Скачать презентацию